数据结构中一些零碎且易忘的知识点
树
- 并查集:
- 并查集的应用:
- 判断连通性、判环
- Kruskal算法=排序+并查集
- 并查集的存储方式
- 逻辑:双亲表示法的树
- 存储:数组
- 并查集的时间复杂度(m为并查集长度)
- find:优化前为 O ( m ) O(m) O(m);优化后为 O ( l o g 2 n ) O(log_{2}n) O(log2n)
- union: O ( 1 ) O(1) O(1)
- 总复杂度:优化前 O ( m 2 ) O(m^2) O(m2);优化后 O ( m ) O(m) O(m)
- 并查集的应用:
- 树、森林、二叉树遍历序列的关系
树 森林 二叉树 先根遍历 先序遍历 先序遍历 后根遍历 中序遍历 中序遍历 关于森林的中序遍历/后序遍历叫法问题:二者指森林的同一种遍历方法,都是先遍历第一棵树的子节点,然后是第一棵树的根节点,然后是第二棵树… 之所以称为中序遍历,是因为要先处理完一棵树再处理另一棵树。
图
- DFS与BFS算法的应用:
- DFS:
- 判断图的(强)连通性
- 无向图的连通性:若从任意一个节点出发,仅需一次DFS就可以访问图中所有节点,则该无向图就是连通的
- 有向图的强连通性:从任意一个节点v出发DFS,若可以遍历该有向图的所有节点,则此时将该有向图的所有边反向,再次从节点v出发进行DFS,若能够再次遍历该有向图的所有节点,则表示该有向图是强连通图
- 判断图中是否有环(回路)
- 欧拉回路求解:若一条路径能不重复的包含图中所有边,则称该路径为欧拉路径。若一条回路(从一个节点出发又能回到该节点的路径)是欧拉路径,则称为欧拉回路。DFS可以判断图中是否存在欧拉回路
- 迷宫
- 判断二分图
- 判断图的(强)连通性
- BFS:
- 求解单源最短路径问题(只适用于无权图)
- 迷宫
- 判断二分图
- DFS:
- 最短路径
- 有无环(回路)对Dijkstra算法并无影响,但Dijkstra算法不能求解存在负权值边的图;Floyd算法可以求带有负权值边的图,但图中不能存在负权回路(因为带有负权回路的图没有最短路径)
- Dijkstra算法是解决单源最短路径类问题,floyd算法是解决多源最短路径(指图中任意两个顶点之间的最短路径)类问题
- Dijkstra算法属于贪心算法,floyd算法属于动态规划算法
- 判断有向图是否有环(回路)的几种方法:
- 深度优先遍历:若在遍历过程中遇到要访问的节点已在栈中就是有环
- 拓扑排序:找不到拓扑序列必定有环
- 拓扑排序
- 在拓扑排序算法中,为暂存入度为零的顶点可以使用栈,也可以使用队列。(因为只要入了栈/队列,就都是入度为零的,从哪个入度为零的先开始都无所谓)
- 采用深度优先遍历也可实现拓扑排序
相关文章:

数据结构中一些零碎且易忘的知识点
树 并查集: 并查集的应用: 判断连通性、判环Kruskal算法排序并查集 并查集的存储方式 逻辑:双亲表示法的树存储:数组 并查集的时间复杂度(m为并查集长度) find:优化前为 O ( m ) O(m) O(m)&…...
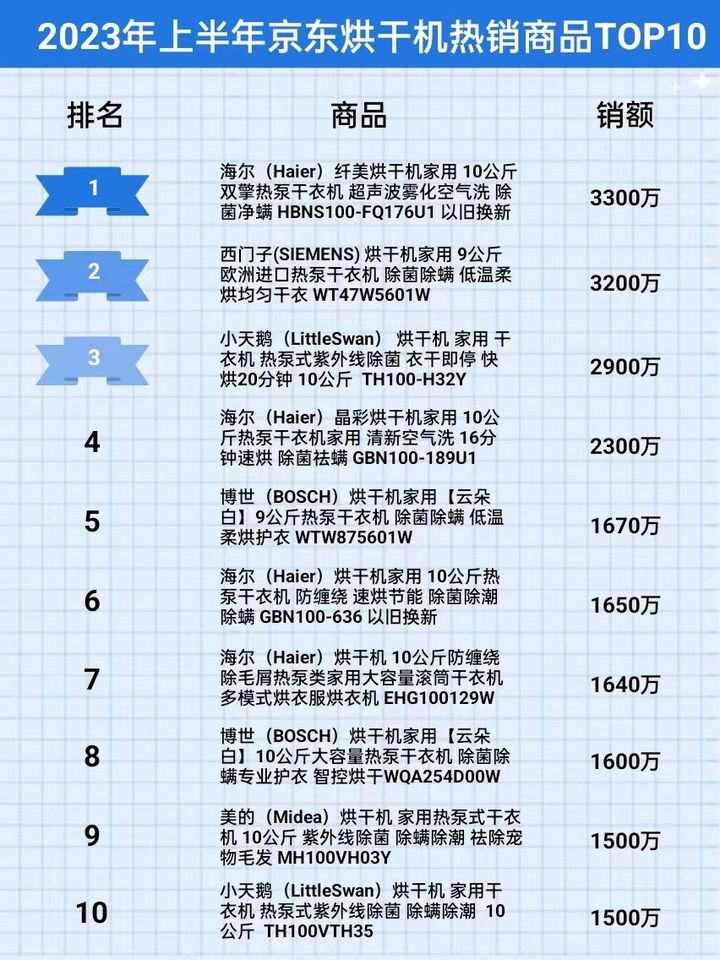
2023上半年京东烘干机行业品牌销售排行榜(京东商品数据)
随着人们消费水平的提高,追求健康品质消费的用户越来越多,这样的消费升级为市场的发展带来很大的动力。同时,随着洗衣机市场趋向饱和,增长趋于平缓,更新换代和结构升级成为行业的主旋律。 在这一市场背景下࿰…...

ADS版图画封装学习笔记
ADS版图画封装 因为晶体管ATF54143在ADS中是没有封装的,所以要在ADS中画ATF54143的封装,操作步骤如下: 在ADS中新建layout,命名为ATF54143_layout, 根据datasheet知道封装的大小,进行绘制 在layout的con…...
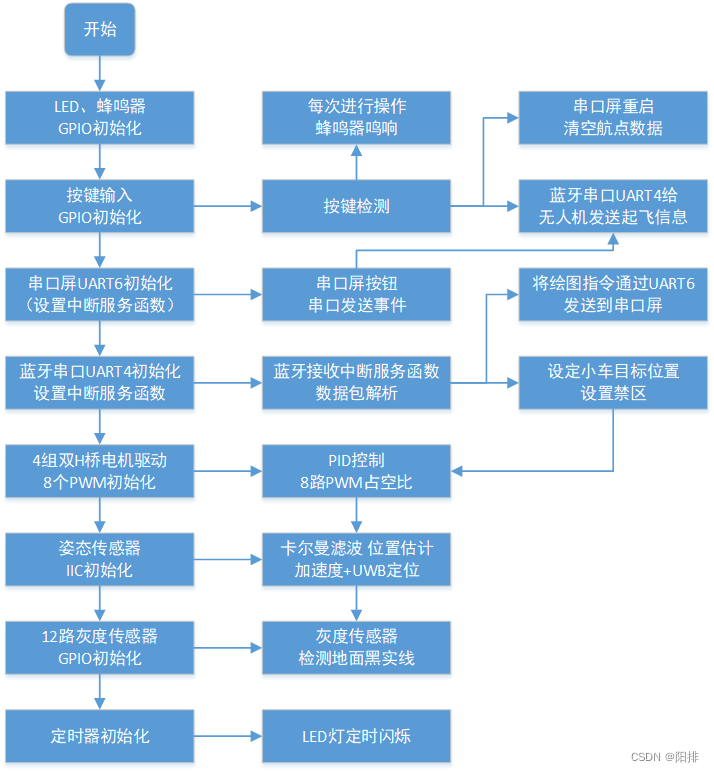
空地协同智能消防系统——无人机、小车协同
1 题目 1.1 任务 设计一个由四旋翼无人机及消防车构成的空地协同智能消防系统。无人机上安装垂直向下的激光笔,用于指示巡逻航迹。巡防区域为40dm48dm。无人机巡逻时可覆盖地面8dm宽度区域。以缩短完成全覆盖巡逻时间为原则,无人机按照规划航线巡逻。发…...

篇二十二:解释器模式:处理语言语法
篇二十二:"解释器模式:处理语言语法" 开始本篇文章之前先推荐一个好用的学习工具,AIRIght,借助于AI助手工具,学习事半功倍。欢迎访问:http://airight.fun/。 另外有2本不错的关于设计模式的资料…...
【LeetCode 75】第二十一题(1207)独一无二的出现次数
目录 题目: 示例: 分析: 代码运行结果: 题目: 示例: 分析: 用两个unordered_map来分别存放每个数字的出现次数和出现的次数这个数,有点绕,比如说有给的数组有两个1,那么第一个map存放的是(1,2),表示1这个数子出现了两次,而第二个map存放的是(2,true),表示有出现次数为2的数…...

node中使用express+mongodb实现分页查询
文章目录 引言一、分页案例二、查询方法扩展介绍1. find()2. limit()3. skip()4. populate() 总结 引言 在Web应用程序开发中,分页查询是必不可少的功能之一。Node.js提供了许多优秀的工具和框架来实现分页查询,其中最流行的框架之一就是Express。同时&…...

信创优选,国产开源。Solon v2.4.2 发布
Solon 是什么开源项目? 一个,Java 新的生态型应用开发框架。它从零开始构建,有自己的标准规范与开放生态(历时五年,已有全球第二级别的生态规模)。与其他框架相比,它解决了两个重要的痛点&…...

Java HTTP client常见库
前言 每种编程语言里最常用的库恐怕是Http请求库了,如python里的requests包,nodejs里的request模块。 在Java世界里,也是百花齐放,山头林立。常用的有: HttpURLConnection: 最早的JDK提供的类Java 11提供的HttpClien…...

【Java基础教程】(四十四)IO篇 · 上:File类、字节流与字符流,分析字节输出流、字节输入流、字符输出流和字符输入流的区别~
Java基础教程之IO操作 上 🔹本节学习目标1️⃣ 文件操作类:File2️⃣ 字节流与字符流2.1 字节输出流:OutputStream2.2 字节输入流:InputStream2.3 字符输出流:Writer2.4 字符输入流:Reader2.5 字节流与字符…...

电商数据获取:网络爬虫还是付费数据接口?
随着电商行业的迅速发展,对电商数据的需求也越来越大。在获取电商数据时,常常面临一个选择:是自己编写网络爬虫进行数据爬取,还是使用现有的付费数据接口呢?本文将从成本、可靠性、数据质量等多个角度进行分析…...

树形结构——二叉树类型
本文主要介绍树形结构中的二叉树类型,包括二叉树、平衡二叉树、二叉查找树和完全二叉树; 1.二叉树 二叉树是一种树形结构,其中每个节点最多有两个子节点,通常称为左子节点和右子节点。二叉树具有以下特点: 每个节点…...

JavaScript对象的方法与原型链
在JavaScript中,对象是一种非常重要的数据类型,它允许我们将多个属性和方法组织在一起。对象的方法和原型链是理解JavaScript中面向对象编程的关键概念。本文将详细讲解对象的方法和原型链,用通俗易懂的方式帮助你深入理解这些概念。 1. 对象…...

Oracle入门初探---第一章 批量创建表、索引并插入测试数据
Oracle系列文章目录 第一章 批量创建表并插入测试数据 文章目录 Oracle系列文章目录前言一、创建表和索引二、向表中加入数据总结 前言 使用数据库,首先要向数据库中加入大量数据,本篇文章提供了一些测试数据 一、创建表和索引 -- 创建数据库和索引 -…...
全面讲解最小二乘法
常见的最小二乘法我们就不多说了,下面主要介绍一下最小二乘法的一些先进方法。 正则化的最小二乘法 在使用常见的最小二乘法进行回归分析时,常常会遇到过拟合的问题,也就是在训练数据集上表现的很好,但是在测试数据集上表现的很…...
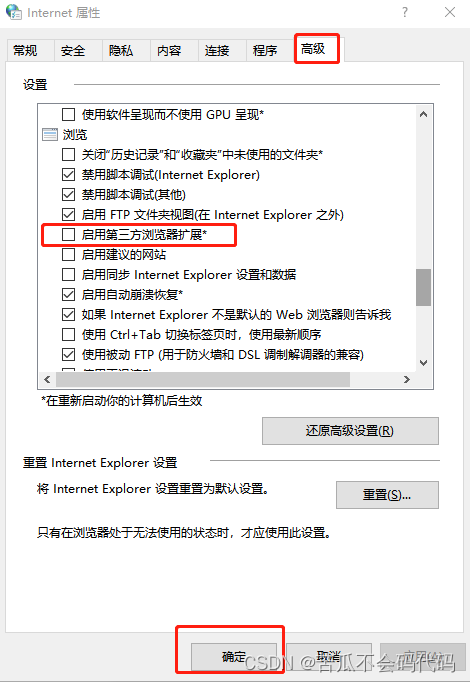
【阻止IE强制跳转到Edge浏览器】
由于微软开始限制用户使用Internet Explorer浏览网站,IE浏览器打开一些网页时会自动跳转到新版Edge浏览器,那应该怎么禁止跳转呢? 1、点击电脑左下角的“搜索框”或者按一下windows键。 2、输入“internet”,点击【Internet选项…...
)
C++/Linux项目——日志系统(简介)
一,日志系统的目的 1.⽣产环境的产品为了保证其稳定性及安全性是不允许开发⼈员附加调试器去排查问题, 可以借助⽇志系统来打印⼀些⽇志帮助开发⼈员解决问题 2.上线客⼾端的产品出现bug⽆法复现并解决, 可以借助⽇志系统打印⽇志并上传到服…...

【Redis面试题整理一】
一、Redis定义 Redis 是一种基于内存的数据库,对数据的读写操作都是在内存中完成,读写速度非常快,被广泛应用于缓存方向。并且,Redis 存储的是 KV 键值对数据。 二、Redis为什么不存在并发竞争 对数据类型的操作都是原子性的&a…...

前端权限验证之自定义指令v-permission
自定义指令 在前端处理按钮权限详细代码 在前端处理按钮权限 使用vue自定义指令来v-permission 来控制按钮 详细代码 //index.js文件 import permission from ./permissionconst install function(Vue) {Vue.directive(permission, permission) }if (window.Vue) {window[p…...
)
c++使用条件变量实现生产消费问题(跨平台)
1. 生产者线程 思路:队列满了的情况下, 触发条件变量wait, 等待消费线程消费后唤醒继续生产. void ProducerThreadFunc() {while(1) { while(/* 容器已满 */) { /* 线程等待, 直到消费者消费后唤醒继续执行 */ }/* 生产动作 */ } }2. 消…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...
C++中vector类型的介绍和使用
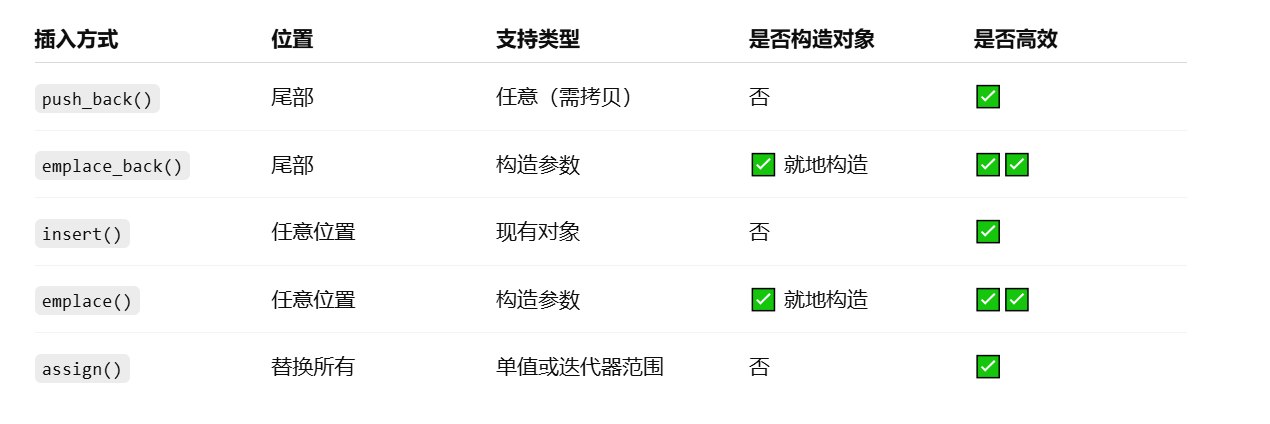
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
