【ESP 保姆级教程】玩转emqx数据集成篇② ——控制台输出动作(多用于测试环境调试功能)
忘记过去,超越自己
- ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️
- ❤️ 本篇创建记录 2023-02-10 ❤️
- ❤️ 本篇更新记录 2023-02-10 ❤️
- 🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝
- 🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请留言轰炸哦!及时修正!感谢支持!
- 🔥 Arduino ESP8266教程累计帮助过超过1W+同学入门学习硬件网络编程,入选过选修课程,刊登过无线电杂志 🔥
快速导读
- 1. 前言
- 2. 实验内容
- 2.1 实验一:监听所有用户上线下线通知
- 2.1.1 找到数据来源
- 2.1.2 规则处理
- 2.1.3 动作
- 2.1.4 确认添加规则
- 2.1.5 测试结果
- 2.2 实验二:获取主题 testTopic上报的内容信息</
相关文章:
)
【ESP 保姆级教程】玩转emqx数据集成篇② ——控制台输出动作(多用于测试环境调试功能)
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-10 ❤️❤️ 本篇更新记录 2023-02-10 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...
MyBatis案例 | 使用映射配置文件实现CRUD操作——添加数据
本专栏主要是记录学习完JavaSE后学习JavaWeb部分的一些知识点总结以及遇到的一些问题等,如果刚开始学习Java的小伙伴可以点击下方连接查看专栏 本专栏地址:🔥JavaWeb Java入门篇: 🔥Java基础学习篇 Java进阶学习篇&…...

2023年,什么样的CRM,才是您最需要的?
春节假期刚刚结束,当大家还沉浸在新春佳节的喜悦中时,很多地方已经争先恐后地奋力开跑了。近日,全国各地方政府相继出台并发布了2023年数字化转型规划,纷纷结合自身的区位特色和优势资源,明确2023年乃至此后数年的数字…...
)
【C语言】编程初学者入门训练(6)
文章目录51. 计算一元二次方程52. 获取月份天数53. 简单计算器54. 线段图案55. 正方形图案56. 直角三角形图案57. 翻转直角三角形图案58. 带空格直角三角形图案59. 金字塔图案60. 翻转金字塔图案51. 计算一元二次方程 问题描述:从键盘输入a, b, c的值,编…...
Java笔记-异常相关
一、异常概述与异常体系结构 Error:Java虚拟机无法解决的严重问题: JVM系统内部错误,资源耗尽,如:StackOverflow \OOM堆栈溢出 处理办法:只能修改代码,不能编写处理异常的代码 Exception:可以处理的异常 &…...

pytest-xdist测试用例并发
官方文档:pytest-xdist初次使用参考:Python测试框架pytest(22)插件 - pytest-xdist(分布式执行)pytest测试框架系列 - Pytest pytest-xdist 分布式、多进程并发执行用例你会用吗?Pytest-xdist并…...
大数据---Hadoop安装jdk简易版
编写自动安装jdk的shell脚本 完整流程: 大数据—Hadoop安装教程(一) 文章目录编写自动安装jdk的shell脚本上传压缩包编写shell脚本vim autoinstall.sh解压更名添加环境运行上传压缩包 在opt目录下创建连个目录install和soft 将压缩包上传到install目录…...

【0基础学爬虫】爬虫基础之爬虫的基本介绍
大数据时代,各行各业对数据采集的需求日益增多,网络爬虫的运用也更为广泛,越来越多的人开始学习网络爬虫这项技术,K哥爬虫此前已经推出不少爬虫进阶、逆向相关文章,为实现从易到难全方位覆盖,特设【0基础学…...
Python 数据库开发实战 - Python与Redis交互篇- 综合案例 - 新闻管理系统 - 缓存新闻数据至redis
接下来这个章节将继续来完成 《新闻管理系统》 这个项目,上一章节我们完成了 “发表新闻” 这个功能,在发表新闻后,什么时候才会缓存该条新闻记录呢?并不是说在发表新闻成功之后就立刻被缓存,而是该新闻被管理员审批通…...
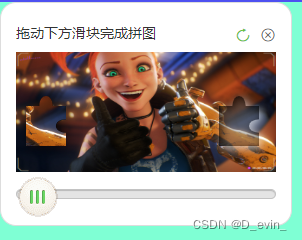
Vue拼图验证
vue-puzzle-verification 封装的一个用于登录验证的拼图的vue组件,使用了canvas画图和拖拽的一些技巧。支持大小、形状、图片、偏差、范围的自定义。 一、安装使用 npm install vue-puzzle-verification 二、main.js里引入 import PuzzleVerification from vue…...
这个神器,让 Python 爬虫如此简单
相信大家应该都写过爬虫,简单的爬虫只需要使用 requests 即可。遇到复杂的爬虫,就需要在程序里面加上请求头和参数信息。类似这种: 我们一般的步骤是,先到浏览器的网络请求中找到我们需要的请求,然后将请求头和参数信…...

网络舆情公关必须把握的四项基本原则
在这个网络媒体占主导的时代,舆情公关进入了网络自媒体时代,有时候可能企业认为是小事儿,也可能在网上掀起轩然大波,所以网络舆情优化成为营销推广工作中重要一环。网络舆情优化的目标是让网络舆论对企业经营发展有利的方向发展&a…...
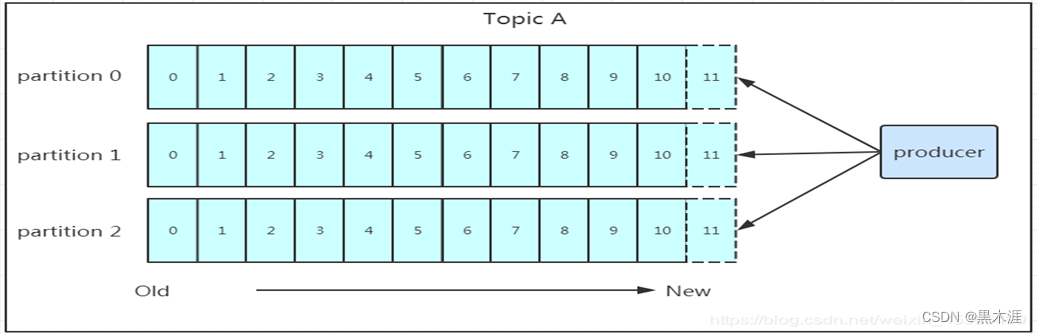
Kafka技术认知
文章目录概念理解名词解释基本架构工作流程Kafka的特性概念理解 Kafka是分布式的基于发布-订阅消息队列。是一个分布式、支持分区的、多副本的,基于 Zookeeper 协调的分布式消息中间件系统,它的最大的特性就是可以实时的处理大量数据以满足各种需求场景…...
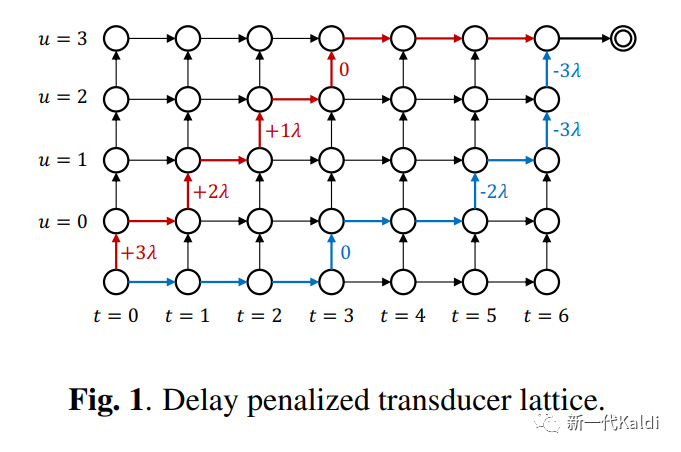
2022年新一代kaldi团队技术输出盘点
目录 1. 技术创新 1.1 Pruned RNN-T loss 1.2 RNN-T 的快速 GPU 解码 1.3 多码本量化索引的知识蒸馏 1.4 RNN-T 和 CTC 的低延时训练 1.5 Zipformer 1.6 Small tricks 2. 模型部署 2.1 Sherpa 2.1 Sherpa-ncnn 3. 更多的 recipe 和模型 参考资料 1. 技术创新 1.1 …...

数据结构复习(三)顺序表oj
目录 27. 移除元素 26. 删除有序数组中的重复项 88. 合并两个有序数组 27. 移除元素 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外…...

2023.2.10每日一题
每日一题题目描述解题核心解法一:模拟题目描述 题目链接:2553. 分割数组中数字的数位 给你一个正整数数组nums,请你返回一个数组answer,你需要将nums中每个整数进行数位分割后,按照nums中出现的相同顺序放入答案数组…...

Homekit智能家居DIY一智能吸顶灯
买灯要看什么因素 好灯具的灯光可以说是家居的“魔术师”,除了实用的照明功能外,对细节的把控也非常到位。那么该如何选到一款各方面合适的灯呢? 照度 可以简单理解为清晰度,复杂点套公式来说照度光通量(亮度&#x…...
关于 OAuth 你又了解哪些?
作者罗锦华,API7.ai 技术专家/技术工程师,开源项目 pgcat,lua-resty-ffi,lua-resty-inspect 的作者。 OAuth 的背景 OAuth,O 是 Open,Auth 是授权,也就是开放授权的意思。OAuth 始于 2006 年&a…...

18. 构造函数和析构函数,构造函数的分类和调用
构造函数和析构函数 构造函数 //没有返回值 不用写void//函数名 与 类名相同//可以有参数 ,可以发生重载//构造函数 由编译器自动调用一次 无须手动调用析构函数 //没有返回值 不用写void函数名 与类名相同 函数名前 加 ~不可以有参数 ,不可以发生重载析构函数 也是由编译器自…...
)
JavaScript设计模式es6(23种)
设计模式简介设计模式代表了最佳的实践,通常被有经验的面向对象的软件开发人员所采用。设计模式是软件开发人员在软件开发过程中面临的一般问题的解决方案。这些解决方案是众多软件开发人员经过相当长的一段时间的试验和错误总结出来的。设计模式是一套被反复使用的…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
