2019蓝桥杯真题平方序列(填空题) C语言/C++
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小明想找到两个正整数 X 和 Y,满足2019<X<Y;2019^2, X^2, Y^2组成等差数列。
请你求出在所有可能的解中,X+Y 的最小值是多少?
运行限制
最大运行时间:1s
最大运行内存: 128M
所需变量
int a = 2019;//由于是填空题,我直接把2019赋值给a了
int x = 2020;//这是为了满足条件x比a大
int y = 2021;//满足条件y大于x也大于a
首先我们拿到这个题的时候,我们的第一感觉就是很难,而却算法所耗费的时间肯定很大,因为我们要不断的去尝试x和y同时满足!
那么我们的第一想法就是每次让x+1,然后也让y+1!仔细想想是不对的,这样肯定会不满足时间要求,时间复杂度太高了
因此我们想到一个更好的方法!
首先我们分析题目,我们要找的数要满足等差数列!
对于等差数列的性质就是第二个数(即x)与第一个数(a)的差值等于第三个数(y)与第二个数(x)的差值
用数学公式表示就是y*y-x*x = x*x - a*a
得到这个后,我们就可以明白了,当x+1,y不用直接+1,而是可以直接取向上取整(根号(2*x*x-a*a))
代码如下:
if(y < sqrt(2*x*x-2019*2019)){y = ceil(sqrt(2*x*x-2019*2019));}
如果对于y变化过大,那么当我们需要调整x的时候,我们就是(向上取整(开根号((y*y+a*a)/2)))
代码如下:
if(y > sqrt(2*x*x-2019*2019)){x = ceil(sqrt((y*y+2019*2019)/2));}
当然啦,终止条件就是满足等差数列性质,即y*y ==(2*x*x-2019*2019)我们就跳出循环!
该算法本人认为比较优,如果有更好的想法,欢迎q我!
完整代码如下(编译器是dev,语言是C语言):
#include <iostream>
#include<math.h>
using namespace std;
int main()
{int a = 2019,x = 2020,y = 2021;while(true){if(y*y ==(2*x*x-2019*2019)){break;}else if(y > sqrt(2*x*x-2019*2019)){x = ceil(sqrt((y*y+2019*2019)/2));}else if(y < sqrt(2*x*x-2019*2019)){y = ceil(sqrt(2*x*x-2019*2019));}}cout<<x+y<<endl;return 0;
}

相关文章:

2019蓝桥杯真题平方序列(填空题) C语言/C++
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小明想找到两个正整数 X 和 Y,满足2019<X<Y;2019^2, X^2, Y^2组成等差数列。 请你求出在所有可能的解中,XY 的最小值是多少?…...
vue中,给一个URL地址,利用FileSaver.js插件下载文件到本地
①首先下载 FileSaver.js 插件 npm install file-saver --save ②在需要的.vue页面引入 import { saveAs } from file-saver 在HTML中引入 <script src"https://cdn.bootcdn.net/ajax/libs/FileSaver.js/2.0.5/FileSaver.min.js"></script> //Fil…...
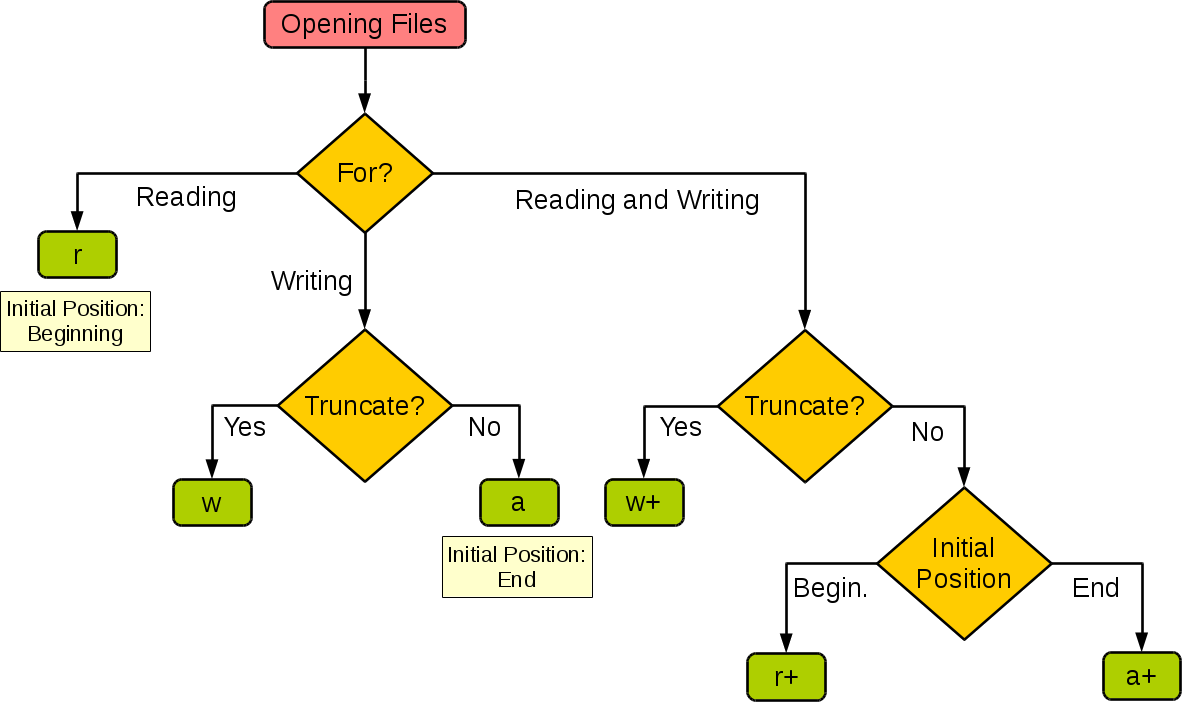
从0开始学python -34
Python3 输入和输出-2 读和写文件 open() 将会返回一个 file 对象,基本语法格式如下: open(filename, mode)filename:包含了你要访问的文件名称的字符串值。mode:决定了打开文件的模式:只读,写入,追加等。…...

瑞典军事研究:从认知心理学的视角探讨军事创新进程
来源:Military Innovation as the Result of Mental Models of Technology 《摘要》 政治紧张局势的加剧和技术发展的进步促使Scandinavian 国家(斯堪的纳维亚半岛,欧洲最大的半岛,有挪威、瑞典两国以及芬兰北端的一小部分。&am…...

【MySQL进阶-08】深入理解innodb存储格式,双写机制,buffer pool底层结构和淘汰策略
MySql系列整体栏目 内容链接地址【一】深入理解mysql索引本质https://blog.csdn.net/zhenghuishengq/article/details/121027025【二】深入理解mysql索引优化以及explain关键字https://blog.csdn.net/zhenghuishengq/article/details/124552080【三】深入理解mysql的索引分类&a…...

5. AOP
一、如何定义一个MethodHandler? 1.Controller注解修饰的类 1.注册成Spring Bean 2.表示它是一个SpringMVC下的Controller 2.在这个类下的方法中,只要被RequestMapping修饰&&方法的形参符合规定(需要看文档) 方法的返回值符合规定…...

ubuntu上尝试libpqxx库链接人大金仓
ubuntu上尝试libpqxx库链接人大金仓 C的项目让使用国产数据库 运维给架了一个人大金仓数据库, Kingbase 8 是基于 PostgreSQL 9.6 做的, 尝试直接使用libpqxx链接数据库。 文章目录ubuntu上尝试libpqxx库链接人大金仓第一步 搭建libpqxx开发环境搜索lib…...
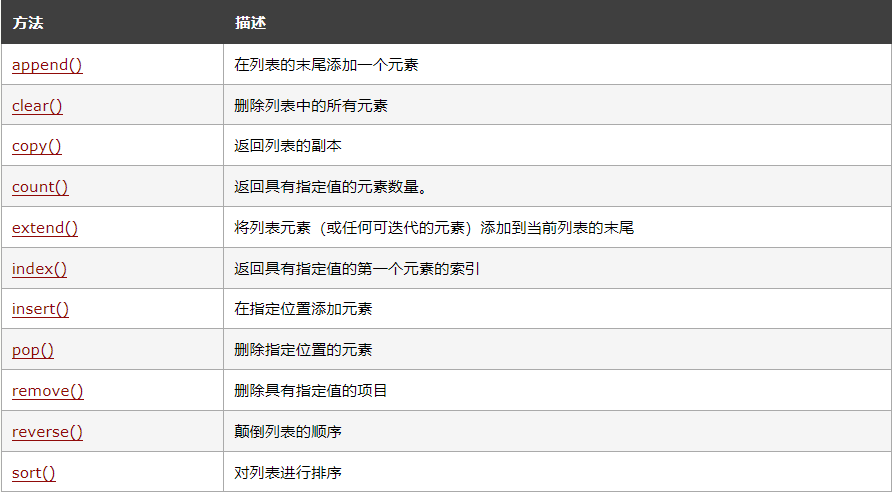
【Python入门第十二天】Python 列表
Python 集合(数组) Python 编程语言中有四种集合数据类型: 列表(List)是一种有序和可更改的集合。允许重复的成员。元组(Tuple)是一种有序且不可更改的集合。允许重复的成员。集合(…...

Android 异步操作库 RxJava
RxJava概述 RxJava 是一种响应式编程,来创建基于事件的异步操作库。基于事件流的链式调用、逻辑清晰简洁。 RxJava 我的理解是将事件从起点(上游)流向终点(下游),中间有很多卡片对数据进操作并传递&#x…...
等级考试试卷(六级)解析)
2021-12-05青少年软件编程(C语言)等级考试试卷(六级)解析
2021-12-05青少年软件编程(C语言)等级考试试卷(六级)解析T1. 电话号码 给你一些电话号码,请判断它们是否是一致的,即是否有某个电话是另一个电话的前缀。比如: Emergency 911 Alice 97 625 999 Bob 91 12 54 26 在这个例子中,我们不可能拨通Bob的电话,因为Emergency的…...
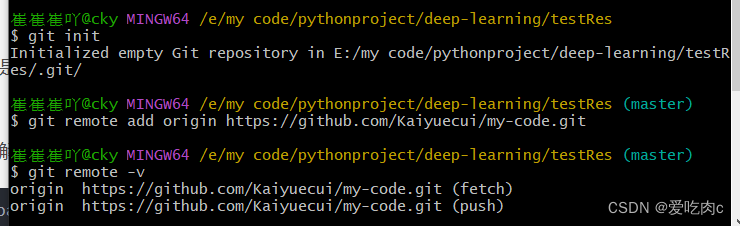
github 使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录一、git与github二、出错的地方1.GitHub没有css样式2、git clone出现错误3、明明创建了responsibility 但git 不显示一、git与github 这个博客写的很好!…...
Kubernetes集群维护—备份恢复与升级
Etcd数据库备份与恢复 需要先安装etcd备份工具yum install etcd -y按不同安装方式执行不同备份与恢复kubeadm部署方式: 备份:ETCDCTL_API3 etcdctl snapshot save snap.db --endpointshttps://127.0.0.1:2379 --cacert/etc/kubernetes/pki/etcd/ca.cr…...
前端开发常用案例(二)
这里写目录标题1.loding加载动画2.全屏加载动画效果3.吃豆豆4.鼠标悬停3D翻转效果5.3D旋转木马效果6.flex弹性布局-酷狗音乐播放列表flex弹性布局-今日头条首页热门视频栏grid网格布局-360图片展示小米商城左侧二级菜单1.loding加载动画 代码如下: <!DOCTYPE h…...

基于springboot+vue的儿科保健计划免疫系统
基于springbootvue的儿科保健计划免疫系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背…...

1.两数之和
难度简单给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序…...

字符串匹配 - 模式预处理:KMP 算法(Knuth-Morris-Pratt)
Knuth-Morris-Pratt算法(简称KMP)是最常用的字符串匹配算法之一。算法简介如下算法解释主要来源于这里,但是通常很难阅读完全,我推荐你直接进入下一节 图例解释部分。我们来观察一下朴素的字符串匹配算法的操作过程。如下图&#…...
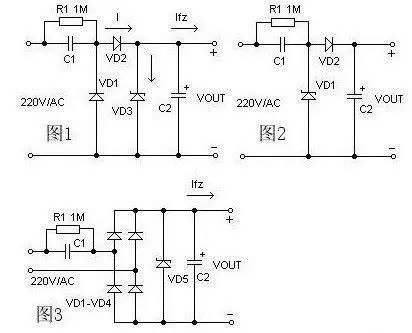
工程师手册:电源设计中的电容选用规则
摘要 电源往往是我们在电路设计过程中最容易忽略的环节。作为一款优秀的设计,电源设计应当是很重要的,它很大程度影响了整个系统的性能和成本。电源设计中的电容使用,往往又是电源设计中最容易被忽略的地方。一、电源设计中电容的工作原理 在…...

【安全开发】专栏文章汇总
安全开发–1–TCP和UDP网络编程 安全开发–2–嗅探邮箱协议口令 安全开发–3–Python实现ARP缓存投毒 安全开发–4–SSH通信工具开发 安全开发–5–编写简单的netcat工具 安全开发–6–一个简单的TCP代理工具开发 安全开发–7–SSH隧道工具开发 安全开发–8–Python实现流量数据…...

视频监控流程图4
<html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"/> <link rel"stylesheet" type"text/css" href"visio.css"/> <title> 视频监控流程图 </title> <…...
)
「JVM 编译优化」Java 语法糖(泛型、自动装箱/拆箱、条件编译)
「JVM 编译优化」Java 语法糖(泛型、自动装箱/拆箱、条件编译) 语法糖可以看做事前端编译期的一些小把戏;虽不会提供实质性的功能改进,但它们或能提高效率,或能提升语法的严谨性,或能减少编码出错的机会&a…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
