Leetcode.995 K 连续位的最小翻转次数
题目链接
Leetcode.995 K 连续位的最小翻转次数
rating : 1835
题目描述
给定一个二进制数组 n u m s nums nums 和一个整数 k k k 。
k k k位翻转 就是从 n u m s nums nums 中选择一个长度为 k k k 的 子数组 ,同时把子数组中的每一个 0 0 0 都改成 1 1 1 ,把子数组中的每一个 1 1 1 都改成 0 0 0 。
返回数组中不存在 0 0 0 所需的最小 k k k位翻转 次数。如果不可能,则返回 − 1 -1 −1 。
子数组 是数组的 连续 部分。
示例 1:
输入:nums = [0,1,0], K = 1
输出:2
解释:先翻转 A[0],然后翻转 A[2]。
示例 2:
输入:nums = [1,1,0], K = 2
输出:-1
解释:无论我们怎样翻转大小为 2 的子数组,我们都不能使数组变为 [1,1,1]。
示例 3:
输入:nums = [0,0,0,1,0,1,1,0], K = 3
输出:3
解释:
翻转 A[0],A[1],A[2]: A变成 [1,1,1,1,0,1,1,0]
翻转 A[4],A[5],A[6]: A变成 [1,1,1,1,1,0,0,0]
翻转 A[5],A[6],A[7]: A变成 [1,1,1,1,1,1,1,1]
提示:
- 1 ≤ n u m s . l e n g t h ≤ 1 0 5 1 \leq nums.length \leq 10^5 1≤nums.length≤105
- 1 ≤ k ≤ n u m s . l e n g t h 1 \leq k \leq nums.length 1≤k≤nums.length
解法:贪心 + 差分
假设前 i − 1 i - 1 i−1 个元素已经是全为 1 1 1 了,第 i i i 个元素是 0 0 0。我们要想翻转这个元素,就要翻转 [ i , i + k − 1 ] [i,i + k - 1] [i,i+k−1] 整个区间的元素。并且这也是翻转第 i i i 位元素最少的操作次数,对于每一个元素都是如此。
需要注意的是:对于一个需要翻转的元素,它的反转次数必须是奇数,如果是偶数的话,就相当于没有翻转。
我们可以使用差分数组来优化翻转的过程,比如要翻转区间 [ i , i + k − 1 ] [i , i + k - 1] [i,i+k−1],我们只需要让 [ i , i + k − 1 ] [i , i + k - 1] [i,i+k−1] 中每一个元素的翻转次数 + 1 +1 +1,即 d i f f [ i ] + + , d i f f [ i + k ] − − diff[i]++ , diff[i + k]-- diff[i]++,diff[i+k]−−, d i f f diff diff 就是差分数组。
时间复杂度: O ( n ) O(n) O(n)
C++代码:
class Solution {
public:int minKBitFlips(vector<int>& nums, int k) {int n = nums.size();vector<int> diff(n + 1);int cnt = 0 , ans = 0;for(int i = 0;i < n;i++){cnt += diff[i];//默认初始每一个元素都是 0//nums[i] + cnt 即元素 nums[i] 的翻转次数//如果翻转次数为偶数 , 说明当前元素还是0,需要翻转if((nums[i] + cnt) % 2 == 0){diff[i + 1]++;//此时 i + k > n 说明无法翻转了,直接返回 -1if(i + k > n) return -1;diff[i + k]--;ans++;}}return ans;}
};
相关文章:

Leetcode.995 K 连续位的最小翻转次数
题目链接 Leetcode.995 K 连续位的最小翻转次数 rating : 1835 题目描述 给定一个二进制数组 n u m s nums nums 和一个整数 k k k 。 k k k位翻转 就是从 n u m s nums nums 中选择一个长度为 k k k 的 子数组 ,同时把子数组中的每一个 0 0 0 都改成 1 1 1 …...

PHP8的跳转语句-PHP8知识详解
如果循环条件满足的时候,则程序会一直执行下去。如果需要强制跳出循环,则需要使用跳转语句来完成。PHP8的跳转语句包括break语句、continue语句和goto语句。 1、break语句 break语句的作用是完全终止循环,包括while、do…while、for、switch…...

Idea中maven无法下载源码
今天在解决问题的时候想要下载源码,突然发现idea无法下载,这是真的蛋疼,没办法查看原因,最后发现问题的原因居然是因为Maven,由于我使用的idea的内置的Bundle3的Maven,之前没有研究过本地安装和内置的区别&…...
【linux-keepalive】keepalive避免单点故障,高可用配置
keepalive: [rootproxy ~]# yum install -y keepalived [rootproxy ~]# vim /etc/keepalived/keepalived.conf global_defs {router_id proxy1 //设置路由ID号vrrp_iptables //不添加任何防火墙规则 } vrrp_instance V…...

测试网络模型的FLOPs和params
概念 FLOPS:注意全大写,是floating point operations per second的缩写,意指每秒浮点运算次数,理解为计算速度。是一个衡量硬件性能的指标。 FLOPs:注意s小写,是floating point operations的缩写…...

《树莓派项目实战》第十五节 使用L298N驱动板模块驱动双极42步进电机
目录 15.1 双极步进电机引脚介绍 15.2 连接到树莓派 15.3 编写代码驱动步进电机 在本节,我们将学习如何使用L298N驱动板驱动一个双极42步进电机。该项目涉及到的材料有: 树莓派...
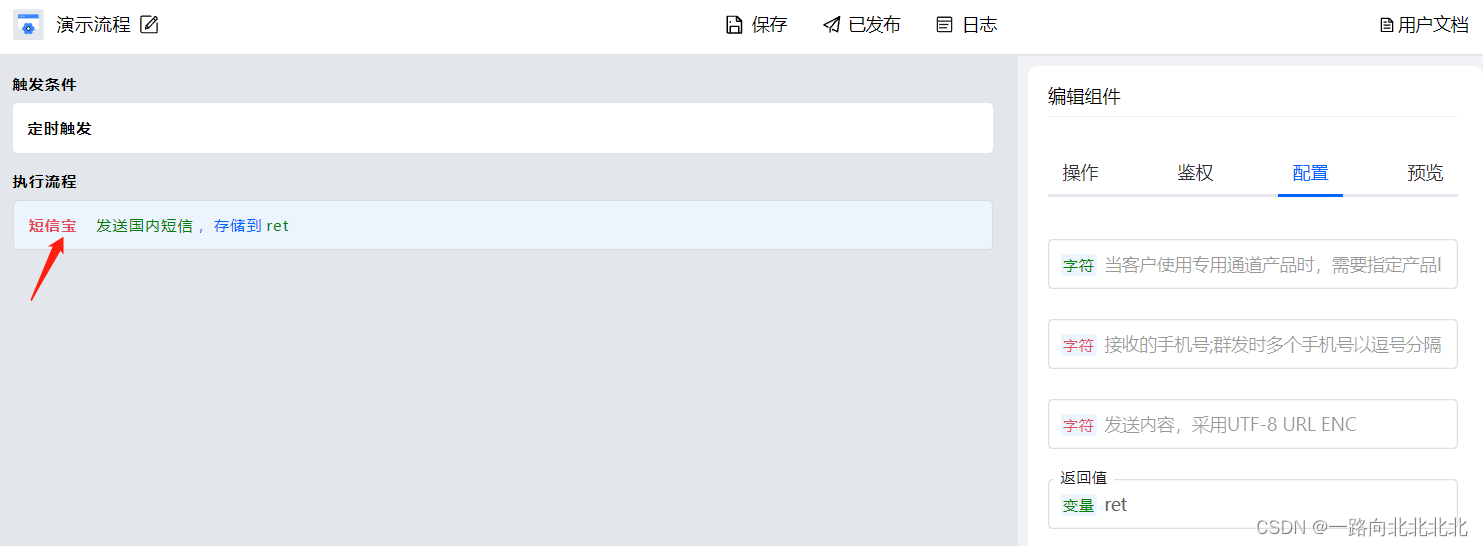
基于短信宝API零代码实现短信自动化业务
场景描述: 基于短信宝开放的API能力,实现在特定事件(如天气预警)或定时自动发送短信(本文以定时群发短信为例)。通过Aboter平台如何实现呢? 使用方法: 首先创建一个IPaaS流程&…...
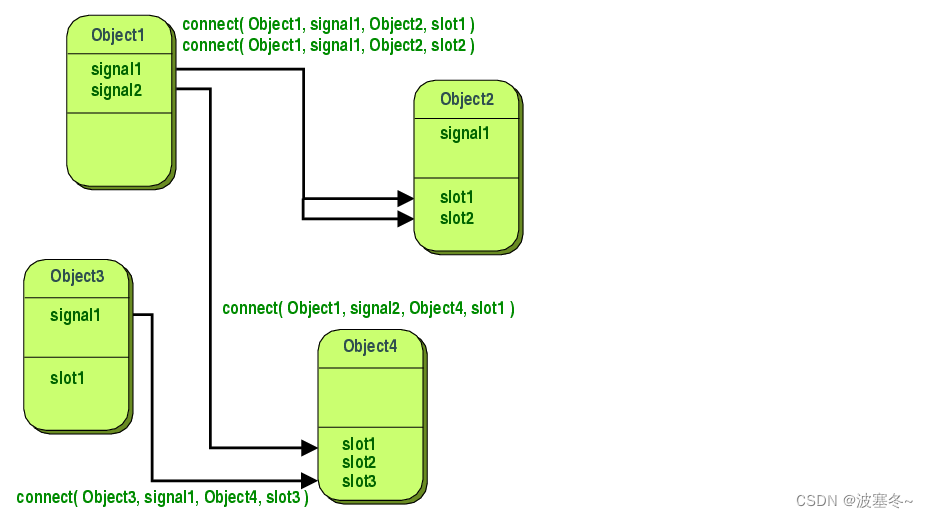
Qt应用开发(基础篇)——信号槽 Signals and Slots
一、前言 Qt成为我们今天拥有的灵活而舒适的工具,除了友好和能够快速开发设计师界面,信号槽机制是最大的核心特征,也是区别于其他开发框架最大的优势。 Qt的信号槽作用于两个对象之间的通信。当一个对象发生了改变,它希望其他关心…...

正则表达式--Notepad++常用的替换
原文网址:正则表达式--Notepad常用的替换_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Notepad使用正则表达式进行替换时的常用的一些示例。 服务器JSON的格式化 例1:将回车去掉,改为正确的JSON格式 搜索: ([^,])(\r)(\n)(\s) 替…...

ES6 对象合并
对象合并 在 JavaScript 中,可以使用不同的方法来合并对象的属性。这样可以将两个或多个对象的属性合并到一个新的对象中。这是在编程中常见的一种操作,尤其在处理配置、选项或数据更新时非常有用。 以下是几种常见的对象合并方法: 1. 使用…...
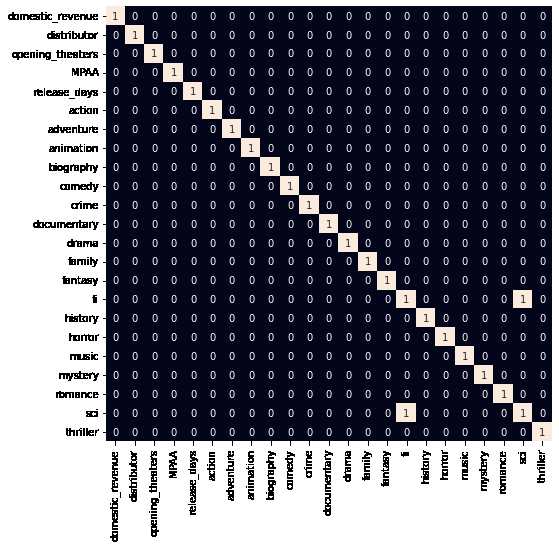
使用线性回归预测票房收入 -- 机器学习项目基础篇(10)
当一部电影被制作时,导演当然希望最大化他/她的电影的收入。但是我们能通过它的类型或预算信息来预测一部电影的收入会是多少吗?这正是我们将在本文中学习的内容,我们将学习如何实现一种机器学习算法,该算法可以通过使用电影的类型…...

一文读懂|RDMA原理
什么是DMA DMA全称为Direct Memory Access,即直接内存访问。意思是外设对内存的读写过程可以不用CPU参与而直接进行。我们先来看一下没有DMA的时候: 无DMA控制器时I/O设备和内存间的数据路径 假设I/O设备为一个普通网卡,为了从内存拿到需要…...
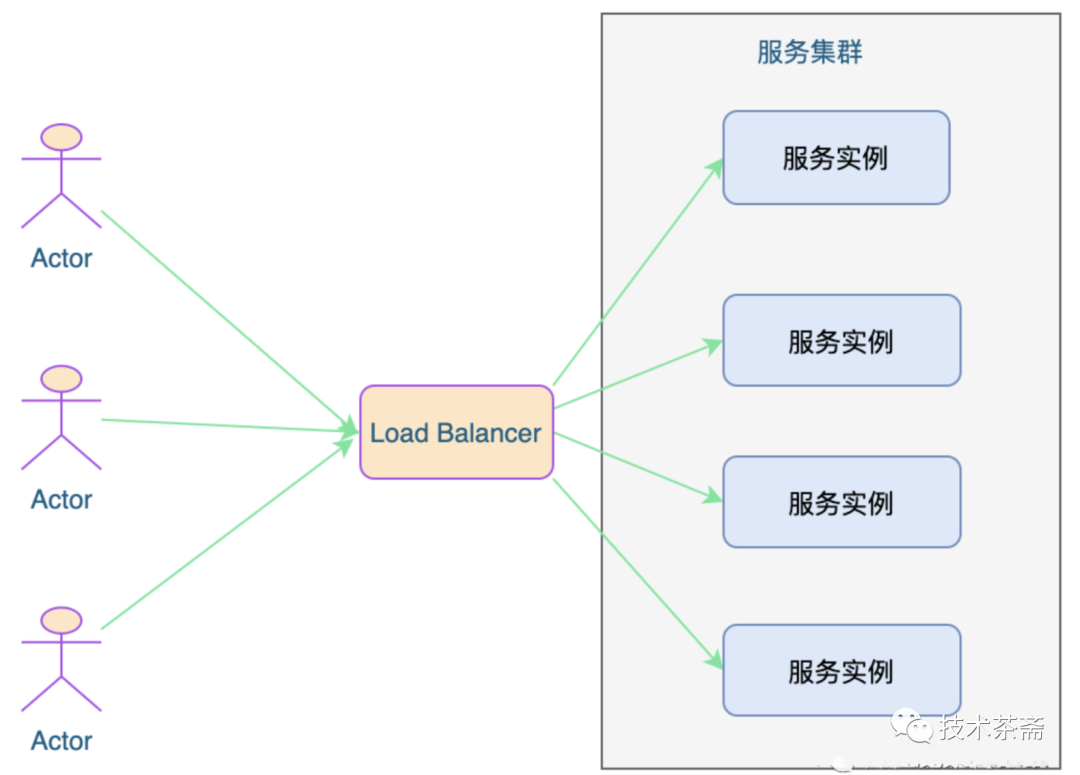
深入理解负载均衡原理及算法
1. 前言 在互联网早期,网络还不是很发达,上网用户少,流量相对较小,系统架构以单体架构为主。但如今在互联网发达的今天,流量请求动辄百亿、甚至上千亿,单台服务器或者实例已完全不能满足需求,这就有了集群。不论是为了实现高可用还是高性能,都需要用到多台机器来扩展服…...
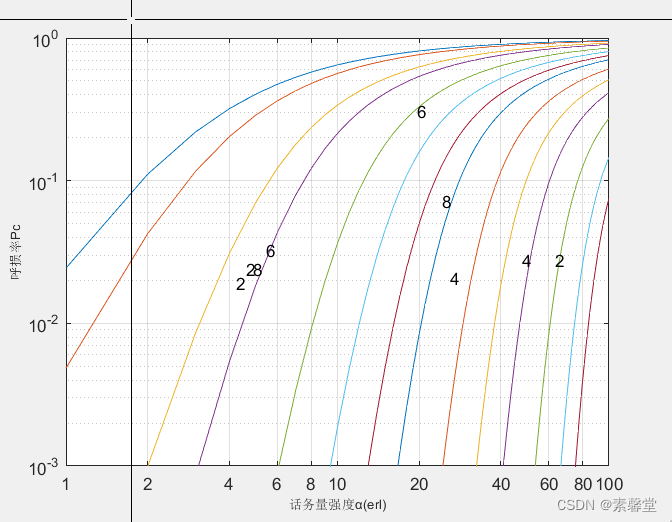
44.实现爱尔兰B公式计算并输出表格(matlab程序)
1.简述 1.话务量定义 话务量指在一特定时间内呼叫次数与每次呼叫平均占用时间的乘积。 话务量反映了电话负荷的大小,与呼叫强度和呼叫保持时间有关。呼叫强度是单位时间内发生的呼叫次数,呼叫保持时间也就是占用时间。 话务量计算方法 话务量公式为…...

【Linux】-- 进程间通信
目录 一、进程间通信介绍 二、管道 1.什么是管道(pipe) 2.重定向和管道 (1)为什么要有管道的存在 (2)重定向和管道的区别 3.匿名管道 (1)匿名管道原理 (2&…...

[PyTorch][chapter 48][LSTM -3]
简介: 主要介绍一下 sin(x): 为 数据 cos(x): 为对应的label 项目包括两个文件 main.py: 模型的训练,验证,参数保存 lstm.py 模型的构建 目录: lstm.py main.py 一 lstm.py # -*- coding: utf-8 -*- "&q…...

xss csrf 攻击
介绍 xss csrf 攻击 XSS: XSS 是指跨站脚本攻击。攻击者利用站点的漏洞,在表单提交时,在表单内容中加入一些恶意脚本,当其他正常用户浏览页面,而页面中刚好出现攻击者的恶意脚本时,脚本被执行,从…...
如何使用win10专业版系统自带远程桌面公司内网电脑,从而实现居家办公?
使用win10专业版自带远程桌面公司内网电脑 文章目录 使用win10专业版自带远程桌面公司内网电脑 在现代社会中,各类电子硬件已经遍布我们身边,除了应用在个人娱乐场景的消费类电子产品外,各项工作也离不开电脑的帮助,特别是涉及到数…...

leetcode做题笔记62
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径? 思路一…...

图论 <最短路问题>模板
图论 <最短路问题> 有向图 1.邻接矩阵,稠密图 2.邻接表 (常用)单链表,每一个点都有一个单链表 ,插入一般在头的地方插, 图的邻接表的存储方式 树的深度优先遍历 特殊的深度优先搜索,…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
