44.实现爱尔兰B公式计算并输出表格(matlab程序)
1.简述
1.话务量定义
话务量指在一特定时间内呼叫次数与每次呼叫平均占用时间的乘积。
话务量反映了电话负荷的大小,与呼叫强度和呼叫保持时间有关。呼叫强度是单位时间内发生的呼叫次数,呼叫保持时间也就是占用时间。
话务量计算方法
话务量公式为:A=C * t。
-
A是话务量,单位为erl(爱尔兰);
-
C是呼叫次数,单位是次/小时;
-
t是每次呼叫平均占用时长,单位是小时/次。
单位时间内的话务量等于使用相同时间单位的呼叫强度与呼叫保持时间之乘积,其单位为爱尔兰( Erlang)。例如:呼叫强度=1800次/小时,呼叫保持时间=(1/60)小时/次,则话务量=1800次/小时 X (1/60)小时/次=30 Erl。
一般话务量又称小时呼,统计的时间范围是1个小时。由此可以看出,爱尔兰Erl是一个无量纲的量,只是为纪念爱尔兰这个人而设立的单位。
在移动电话系统中,话务量可分为流入话务量和完成话务量。流入话务量取决于单位时间内发生的平均呼叫次数与每次呼叫平均占用无线波道的时间,在系统流入的话务量中,完成接续的那部分话务量称作完成话务量,未完成接续的那部分话务量称做损失话务量,损失话务量与流入话务量之比称为呼损率。(当多个信道共用时,通常总是用户数大于信道数,当多个用户同时要求服务而信道数不够的时候,只能让一部分用户先通话,另一部分用户等信道空闲的时候再通话。后一部分用户因无空闲信道而不能通话,即为呼叫失败,简称呼损)。
流入话务量=完成话务量+损失话务量;
损失话务量=流入话务量 * 呼叫损失率(呼损率)
2.爱尔兰B公式和爱尔兰C公式的计算
计算爱尔兰即时拒绝系统的时间阻塞率的爱尔兰B公式表示为
s表示系统中继线的数目,a表示到达系统的呼叫量。
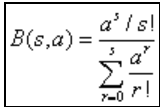
计算爱尔兰等待制系统的呼叫等待概率的爱尔兰C公式表示为
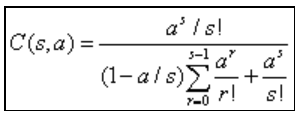
给出两个公式的Matlab实现代码
爱尔兰B公式:
-
function p=Erlang_B_Formula(s,a); -
sum=0; -
for r=0:s%用一个for循环实现求和 -
sum=sum+a^r/factorial(r); -
end -
p=a^s/(sum*factorial(s));
爱尔兰C公式:
-
function p=Erlang_C_Formula(s,a); -
sum=a^s/(factorial(s)*(1-a/s)); -
for k=0:s-1%用for循环实现求和 -
sum=sum+a^k/factorial(k); -
end -
p=a^s/(factorial(s)*(1-a/s)*sum);
简单方法:
爱尔兰B公式:
function p=Erlang_B_Formula_1(s,a)
p=a^s/(factorial(s)*sum(a.^[0:s]./factorial([0:s])));
爱尔兰C公式:
function p=Erlang_C_Formula_1(s,a)
p=a^s/(factorial(s)*((1-a/s)*sum(a.^[0:s-1]./factorial([0:s-1]))+a^s/factorial(s)));
另外,已知B(s,a),a或C(s,a),a,可以反推s。
(这个编辑器实在是太难用了= =,代码块竟然没有matlab版的,差评,一颗星都不给~)
2.代码
function ErlangB
clc;
pn=[];
s=[];
x=1:100; %横坐标范围
m=[4 5 8 10 15 20 25 30 40 50 60 75 90 100]; %交换机出线容量
L=length(m);
for i=1:L
for a=1:100 %流入话务量强度
for k=1:m(i)
s=[s,a.^k/factorial(k)];
add=sum(s);
end
pn0=(a.^m(i)/factorial(m(i)))./add;
pn=[pn,pn0]; %顾客被拒绝的概率
s=[];
end
loglog(x,pn); %对数坐标
set(gca,'XGrid','on'); %画网格线
set(gca,'XMinorTick','off');
set(gca,'XTick',[1 2 4 6 8 10 20 40 60 80 100]); %x坐标轴刻度设置
set(gca,'XMinorGrid','off');
set(gca,'Ylim',[0.001 1]); %限定纵坐标的取值范围
set(gca,'YGrid','on');
set(gca,'YMinorTick','off');
hold on
pn=[];
end
xlabel('话务量强度α(erl)','fontsize',8);
ylabel('呼损率Pc','fontsize',8);
for j=1:3 %输入y轴坐标值
gtext('2');
gtext('4');
gtext('6');
gtext('8');
end
gtext('m=4'); %用鼠标在图形上输入注释
for i=2:L
gtext(int2str(m(i)));
end
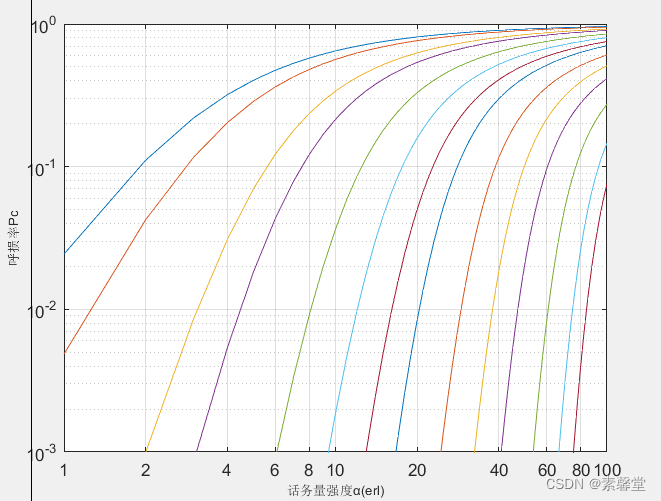
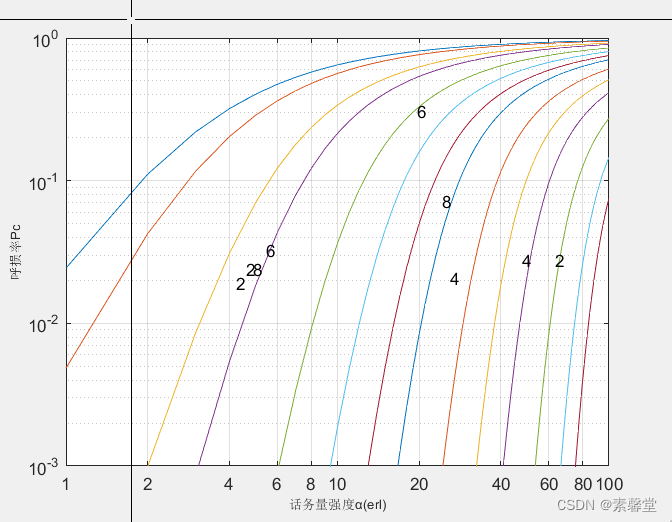
3.运行结果
相关文章:

44.实现爱尔兰B公式计算并输出表格(matlab程序)
1.简述 1.话务量定义 话务量指在一特定时间内呼叫次数与每次呼叫平均占用时间的乘积。 话务量反映了电话负荷的大小,与呼叫强度和呼叫保持时间有关。呼叫强度是单位时间内发生的呼叫次数,呼叫保持时间也就是占用时间。 话务量计算方法 话务量公式为…...

【Linux】-- 进程间通信
目录 一、进程间通信介绍 二、管道 1.什么是管道(pipe) 2.重定向和管道 (1)为什么要有管道的存在 (2)重定向和管道的区别 3.匿名管道 (1)匿名管道原理 (2&…...

[PyTorch][chapter 48][LSTM -3]
简介: 主要介绍一下 sin(x): 为 数据 cos(x): 为对应的label 项目包括两个文件 main.py: 模型的训练,验证,参数保存 lstm.py 模型的构建 目录: lstm.py main.py 一 lstm.py # -*- coding: utf-8 -*- "&q…...

xss csrf 攻击
介绍 xss csrf 攻击 XSS: XSS 是指跨站脚本攻击。攻击者利用站点的漏洞,在表单提交时,在表单内容中加入一些恶意脚本,当其他正常用户浏览页面,而页面中刚好出现攻击者的恶意脚本时,脚本被执行,从…...
如何使用win10专业版系统自带远程桌面公司内网电脑,从而实现居家办公?
使用win10专业版自带远程桌面公司内网电脑 文章目录 使用win10专业版自带远程桌面公司内网电脑 在现代社会中,各类电子硬件已经遍布我们身边,除了应用在个人娱乐场景的消费类电子产品外,各项工作也离不开电脑的帮助,特别是涉及到数…...

leetcode做题笔记62
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径? 思路一…...

图论 <最短路问题>模板
图论 <最短路问题> 有向图 1.邻接矩阵,稠密图 2.邻接表 (常用)单链表,每一个点都有一个单链表 ,插入一般在头的地方插, 图的邻接表的存储方式 树的深度优先遍历 特殊的深度优先搜索,…...
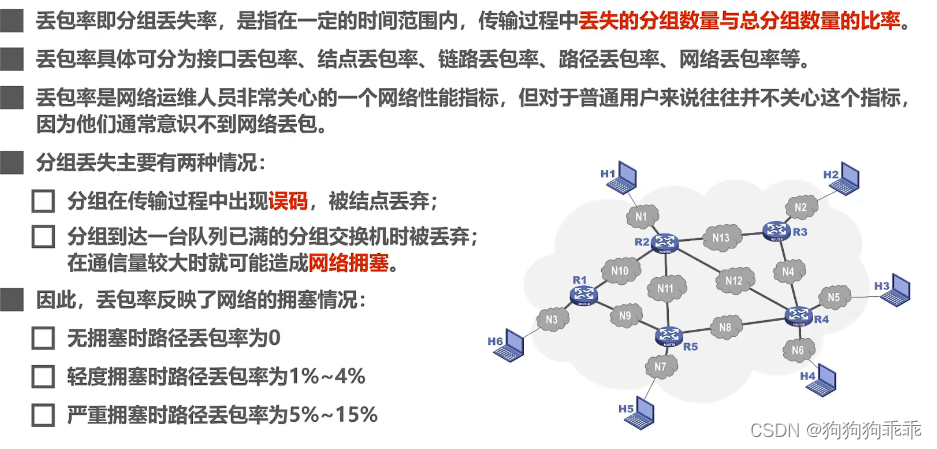
计算机网络性能指标
比特:数据量的单位 KB 2^10B 2^13 bit 比特率:连接在计算机网络上的主机在数字通道上传送比特的速率 kb/s 10^3b/s 带宽:信号所包含的各种频率不同的成分所占据的频率范围 Hz 表示在网络中的通信线路所能传送数据的能力(…...

vue + elementUI 实现下拉树形结构选择部门,支持多选,支持检索
vue elementUI 实现下拉树形结构选择部门,支持多选,支持检索 <template><div><el-select v-model"multiple?choosedValue:choosedValue[0]" element-loading-background"rgba(0,0,0,0.8)":disabled"disableFl…...
招投标系统简介 企业电子招投标采购系统源码之电子招投标系统 —降低企业采购成本 tbms
功能模块: 待办消息,招标公告,中标公告,信息发布 描述: 全过程数字化采购管理,打造从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通供应商门户具备内外协同的能力,为外…...
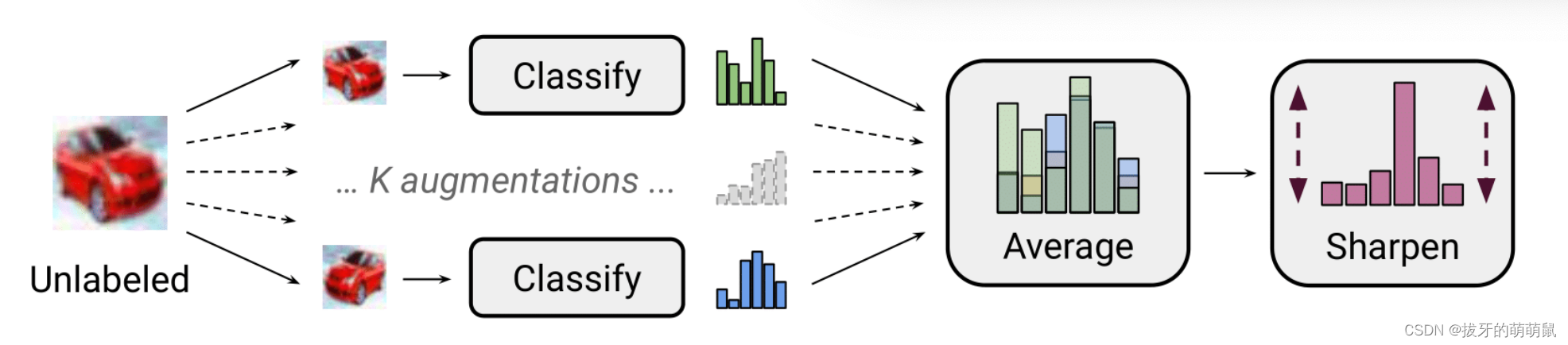
半监督学习(主要伪标签方法)
半监督学习 1. 引言 应用场景:存在少量的有标签样本和大量的无标签样本的场景。在此应用场景下,通常标注数据是匮乏的,成本高的,难以获取的,与之相对应的是却存在大量的无标注数据。半监督学习的假设:决策…...
)
datePicker一个或多个日期组件,如何快捷选择多个日期(时间段)
elementUI的组件文档中没有详细说明type"dates"如何快捷选择一个时间段的日期,我们可以通过picker-options参数来设置快捷选择: <div class"block"><span class"demonstration">多个日期</span><el…...

【语音合成】微软 edge-tts
目录 1. edge-tts 介绍 2. 代码示例 1. edge-tts 介绍 https://github.com/rany2/edge-tts 在Python代码中使用Microsoft Edge的在线文本到语音服务 2. 代码示例 import asyncio # pip install edge_tts import edge_tts TEXT """给我放首我喜欢听的歌曲…...

elevation mapping学习笔记3之使用D435i相机离线或在线订阅点云和tf关系生成高程图
文章目录 0 引言1 数据1.1 D435i相机配置1.2 协方差位姿1.3 tf 关系2 离线demo2.1 yaml配置文件2.2 launch启动文件2.3 数据录制2.4 离线加载点云生成高程图3 在线demo3.1 launch启动文件3.2 CMakeLists.txt3.3 在线加载点云生成高程图0 引言 elevation mapping学习笔记1已经成…...
ESP32 Max30102 (3)修复心率误差
1. 运行效果 2. 新建修复心率误差.py 代码如下: from machine import sleep, SoftI2C, Pin, Timer from utime import ticks_diff, ticks_us from max30102 import MAX30102, MAX30105_PULSE_AMP_MEDIUM from hrcalc import calc_hr_and_spo2BEATS = 0 # 存储心率 FINGER_F…...

16-4_Qt 5.9 C++开发指南_Qt 应用程序的发布
文章目录 1. 应用程序发布方式2. Windows 平台上的应用程序发布 1. 应用程序发布方式 用 Qt 开发一个应用程序后,将应用程序提供给用户在其他计算机上使用就是应用程序的发布。应用程序发布一般会提供一个安装程序,将应用程序的可执行文件及需要的运行库…...

oracle容灾备份怎么样Oracle容灾备份
随着科学技术的发展和业务的增长,数据安全问题越来越突出。为了保证数据的完整性、易用性和保密性,公司需要采取一系列措施来防止内容丢失的风险。 Oracle是一个关系数据库管理系统(RDBMS),OracleCorporation是由美国软件公司开发和维护的。该系统功能…...

AcWing 4957:飞机降落
【题目来源】https://www.acwing.com/problem/content/4960/【题目描述】 有 N 架飞机准备降落到某个只有一条跑道的机场。 其中第 i 架飞机在 Ti 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 Di 个单位时间,即它最早可以于 Ti 时刻开始降落&…...

强化学习研究 PG
由于一些原因, 需要学习一下强化学习。用这篇博客来学习吧, 用的资料是李宏毅老师的强化学习课程。 深度强化学习(DRL)-李宏毅1-8课(全)_哔哩哔哩_bilibili 这篇文章的目的是看懂公式, 毕竟这是我的弱中弱。 强化…...

uniapp微信小程序 401时重复弹出登录弹框问题
APP.vue 登陆成功后,保存登陆信息 if (res.code 200) {uni.setStorageSync(loginResult, res)uni.setStorageSync(token, res.token);uni.setStorageSync(login,false);uni.navigateTo({url: "/pages/learning/learning"}) }退出登录 toLogout: func…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
