【LeetCode 算法】Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值-前缀和
文章目录
- Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值
- 问题描述:
- 分析
- 代码
- 前缀和
- 前缀和
- Tag
Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值
问题描述:
给你一个整数数组 nums 。一个子数组 [ n u m s l , n u m s l + 1 , . . . , n u m s r − 1 , n u m s r ] [nums_l, nums_{l+1}, ..., nums_{r-1}, nums_{r}] [numsl,numsl+1,...,numsr−1,numsr] 的 和的绝对值 为 a b s ( n u m s l + n u m s l + 1 + . . . + n u m s r − 1 + n u m s r ) abs(nums_l + nums_{l+1} + ... + nums_{r-1} + nums_{r}) abs(numsl+numsl+1+...+numsr−1+numsr) 。
请你找出 n u m s nums nums 中 和的绝对值 最大的任意子数组(可能为空),并返回该 最大值 。
abs(x) 定义如下:
如果 x 是负整数,那么 a b s ( x ) = − x abs(x) = -x abs(x)=−x 。
如果 x 是非负整数,那么 a b s ( x ) = x abs(x) = x abs(x)=x 。
1 < = n u m s . l e n g t h < = 1 0 5 − 1 0 4 < = n u m s [ i ] < = 1 0 4 1 <= nums.length <= 10^5\\ -10^4 <= nums[i] <= 10^4 1<=nums.length<=105−104<=nums[i]<=104
分析
暴力
最简单的方法就是枚举出所有可能的子数组,计算其和的绝对值,然后取max。但是子数组的数量规模是 N 2 N^2 N2,所以暴力会TLE,而且即使计算出了子数组,计算其和也是需要时间的。
因为最终需要知道子数组的和的绝对值的最大值。
要得到这样的最大值,那么子数组的和sum一定要尽可能的大,或者尽可能的小,即最大的正数或者最小的负数。
因此只需要在数组中找到子数组和最大的 s u m > = 0 sum>=0 sum>=0,或者 s u m < 0 sum<0 sum<0,sum的最小负数。
到这里,就和某个问题很像了
可以利用前缀和的思路,进行累加 s u m sum sum,然后与之前最小的 p r e m i n premin premin, s u m − p r e m i n sum-premin sum−premin,此时 s u m − p r e m i n sum-premin sum−premin,就是可能的正数的最大子数组和。
同样的 s u m − p r e m a x sum- premax sum−premax,就是可能的负数的最小子数组和。
代码
前缀和
public int maxAbsoluteSum(int[] nums) {int n = nums.length, ans = nums[0];int premax = 0,premin = 0;int sum = 0 ;for(int i = 0;i<n;i++){ sum += nums[i]; int a = sum - premin; // 非负数的最大int b = premax -sum;//负数的绝对值最大ans = Math.max(ans,Math.max(b,a));premin = Math.min(sum,premin);premax = Math.max(sum,premax);}return ans;}
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( 1 ) O(1) O(1)
前缀和
public int maxAbsoluteSum(int[] nums) {int s = 0, mx = 0, mn = 0;for (int x : nums) {s += x;// mx = Math.max(mx, s);// mn = Math.min(mn, s);if (s > mx) mx = s;else if (s < mn) mn = s; // 效率更高的写法}return mx - mn; }
时间复杂度 O ( N ) O(N) O(N)
空间复杂度 O ( 1 ) O(1) O(1)
灵神的代码更精简,不过他是从前缀和的另一个角度来看这个问题的,所以有点不一样。
Tag
Array
Presum
相关文章:

【LeetCode 算法】Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值-前缀和
文章目录 Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值问题描述:分析代码前缀和前缀和 Tag Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值 问题描述: 给你一个整数数组 nums 。一个子数组 [ n u m s l ,…...

怎么建立大型语言模型
建立大型语言模型通常涉及以下主要步骤: 数据收集:收集大规模的文本数据作为模型的训练数据。可以从各种来源获取数据,如互联网、书籍、新闻文章等。数据的质量和多样性对于模型的性能至关重要。 数据预处理:对收集到的数据进行预…...

docker简介和安装
什么是docker? docker是基于Go语言编写的开源容器引擎,是操作系统级别的轻量级虚拟技术。主要用于应用打包、分发、部署。 打包:软件开发过程中,打包是将程序打包成软件包或者镜像的过程;在容器化程序中,打…...

记录问题: servlet获取项目包绝对路径
【2023-8-8 23:46:27 星期二】 如何获取在webapp下的路径?而不是target包下的webapp目录 比如这里应该获取到 F:\Tiam\Desktop\freemarker\freemarker-demo01\src\main\webapp 而readPath总是获取到 F:\Tiam\Desktop\freemarker\freemarker-demo01\target\freemarker-demo0…...

C语言文件操作基本方法
1、文件的分类 ANSI C 的缓冲文件系统 缓冲文件系统 缓冲文件系统是指,系统自动地在内存区为每个正在使用的文件开辟一个缓冲区。 从内存向磁盘输出数据时,必须首先输出到缓冲区中。待缓冲区装满后,再一起输出到磁盘文件中。 从磁盘文件向内…...

SQL 相关子查询 和 不相关子查询、Exists 、Not Exists、 多表连接(包含自连接)
不相关子查询 子查询的查询条件不依赖于父查询,称不相关子查询。子查询可以单独运行的 select stu_id,sex,age from student t where sex(select sexfrom studentwhere stu_id10023 )相关子查询 关联子查询 子查询的查询条件依赖于父查询,称为 相关子…...
)
项目规范 编写规范(范例)
项目目录 目录接口参考 项目目录结构设计,增加部分领域模型后缀强制定义,方便统一编码风格。 controller:请求处理 RestController module:按大业务区分,对多个业务对象数据聚合处理 Component manager:…...

MongoDB数据库操作及操作命令
目录 一、基础概念 二、安装mongod 三、命令交互数据库 (1)数据库命令 (2)集合命令 (3)文档命令 四、Mongoose (1)增加一条数据 (2)插入多个数据 &am…...
之tee)
Linux命令(62)之tee
linux命令之tee 1.tee介绍 linux命令tee于读取标准输入的数据,并将内容输出为文件 2.tee用法 tee [参数] [filename] tee参数 参数说明-a读取标准输入的数据,并将内容追加到文件,而非覆盖-i忽略中断信号 3.实例 3.1.将ls -l输出内容作为…...
搭建Repo服务器
1 安装repo 参考:清华大学开源软件镜像站:Git Repo 镜像使用帮助 2 创建manifest仓库 2.1 创建仓库 git init --bare manifest.git2.2 创建default.xml文件 default.xml文件内容: <?xml version"1.0" encoding"UTF-8" ?…...

安卓:MMKV——键值存储库
目录 一、MMKV介绍 1.特点和优势: 2.使用指南: 3.依赖包: 二、MMKV的常用方法 1、初始化和获取实例: 2、存储数据: 3、读取数据 4、删除数据 5、其他操作: 三、MMKV的使用例子 MainActivityÿ…...

使用Python将图像转换为PDF:一次性解决您的批量转换需求
导语: 在数字化时代,我们经常需要处理大量的图像文件。将这些图像转换为PDF格式可以方便地存档、分享和打印。本文将介绍如何使用Python编程语言将图像批量转换为PDF,并提供了一个简单易用的图形界面来跟踪转换进度。 准备工作 在开始之前…...
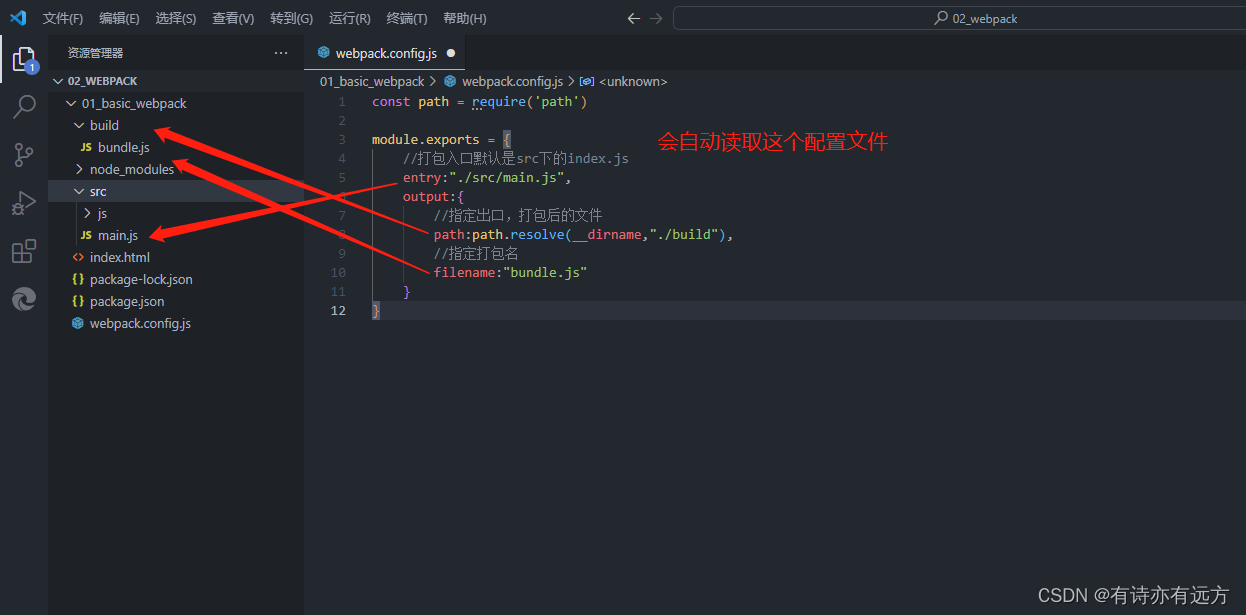
Vue——webpack
webpack 一、Install1.全局安装2.局部安装 二、总结1.打包2.定义脚本3.配置文件定义(webpack.config.js)4.项目重新加载依赖5.webpack打包Css6.style-loader 一、Install 1.全局安装 npm install webpack webpack-cli -g2.局部安装 以项目为单位,一个项…...
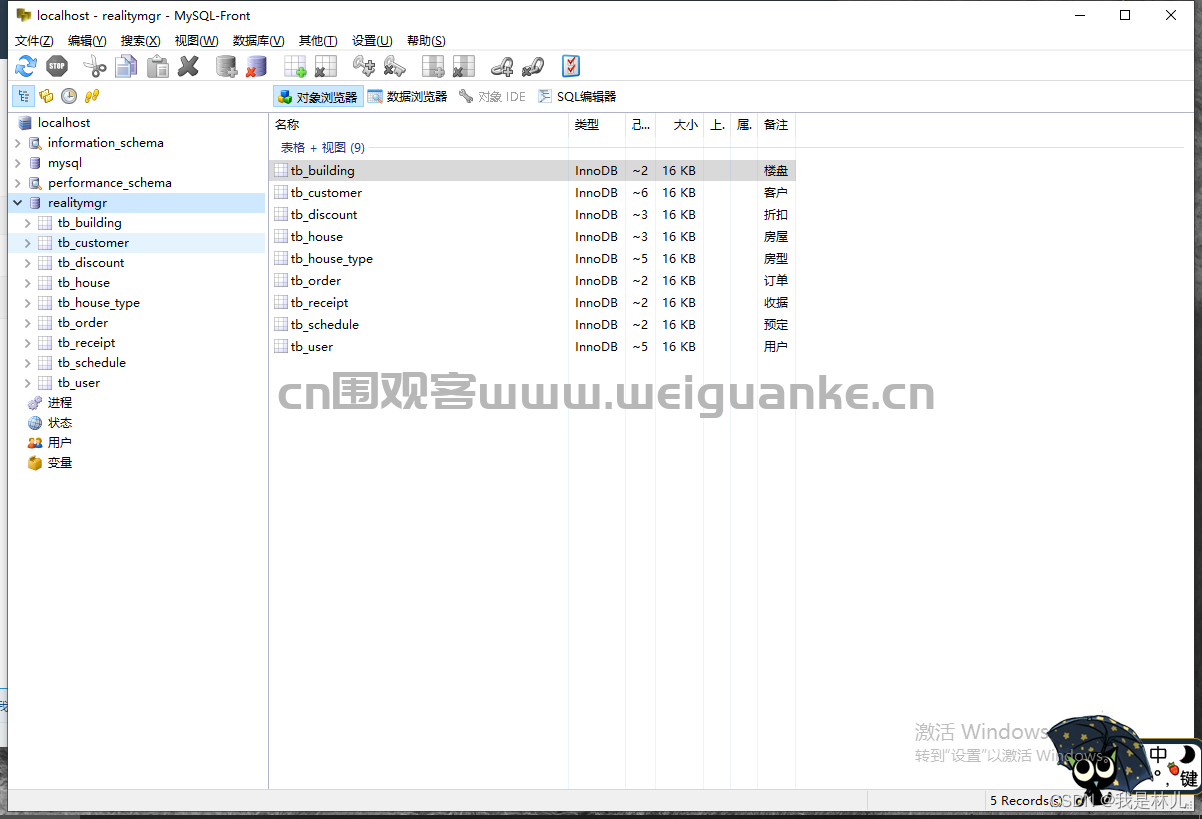
springboot房地产管理java购房租房二手房j客户sp源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 springboot房地产管理 系统1权限:管理员 …...

Gartner 发布影响数据科学和机器学习未来方向重要趋势
出品 | CSDN 云计算 供稿 | Gartner Gartner今日发布了影响数据科学与机器学习(DSML)未来方向的重要趋势。随着DSML行业的快速发展和演变,数据对于人工智能(AI)开发与运用的重要性日益提高,尤其是投资重点…...

72. 编辑距离
题目介绍 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作: 插入一个字符删除一个字符替换一个字符 示例 1: 输入:word1 "horse", word2 &q…...

Android12.0 原生系统SystemUI下拉状态栏和通知栏视图之锁屏通知布局
1.前言 在12.0的系统rom定制化开发中,对于系统原生systemui的锁屏界面的功能也是非常重要的,所以在锁屏页面布局中,也是有通知栏布局的,所以接下来对于息屏亮屏 通知栏布局的相关流程分析,看下亮屏后锁屏页面做了哪些功能 2.原生系统SystemUI下拉状态栏和通知栏视图之锁…...
周末在家值班,解决几个月前遗忘的Bug
问题: 周末被迫在家值班,无聊之际打开尘封已久的Bug清单,发现有Bug拖了几个月还没解决… 场景是这样子的,有个功能是拿Redis缓存热点数据进行展示,暂且称它为功能A,有个另外的功能B,它会去更新缓…...
文本三剑客(sed))
Shell编程基础(十五)文本三剑客(sed)
文本三剑客(sed) 使用场景基本语法实例命令列表 使用场景 sed提供了一种面交互的方式修改文件内容。 它是一行一行处理,可以通过正则匹配要修改的部分 基本语法 基本语法 sed [-opt] command files(多个文件 空格隔开) sed 使用正则 sed -…...
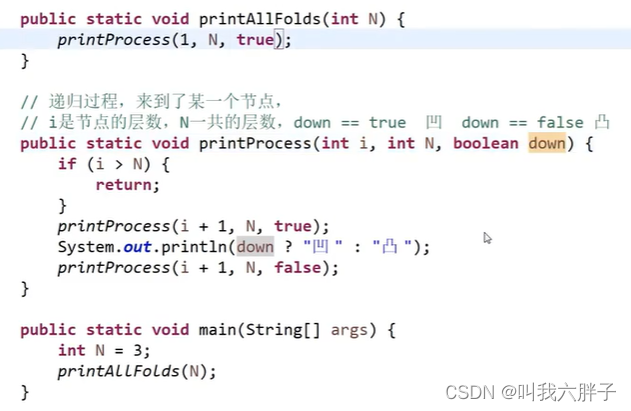
5,二叉树【p6-p7】
二叉树 5.1二叉树5.1.1例1:用递归和非递归两种方式实现二叉树的先序、中序、后序遍历5.1.1.1递归序的先序、中序、后序遍历先序遍历:中序遍历:后序遍历: 5.1.1.2非递归序的先序、中序、后序遍历先序遍历:中序遍历&…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
