SQL 单行子查询 、多行子查询、单行函数、聚合函数 IN 、ANY 、SOME 、ALL
单行子查询
子查询结果是 一个列一行记录
select a,b,c
from table
where a >(select avg(xx) from table )
还支持这种写法,这种比较少见
select a,b,c
from table
where (a ,b)=(select xx,xxx from table where col=‘000’ )
多行子查询
子查询结果是 一个列多行记录
select a,b,c
from table
where a > [ some | any | ALL ](select avg(xx) from table group by col )
单行函数 VS 聚合函数
单行函数 可以嵌套 len,ROUND 等
聚合函数 不能对包含聚合或子查询的表达式执行聚合函数。
但 Oracle 数据库 支持聚合函数嵌套
IN、SOME 、ANY、ALL
In
等于列表中 任意一个
where xxx in (select distinct col from t)
some | any | all
some、any:需要和单行比较符一起使用,和子查询返回的某一个值比较
ALL: 需要和单行比较符,和子查询返回的所有值比较
some 、any 效果一样
where xxx [>=、<=、>、<] some | any | all (select distinct col from t)
相关文章:

SQL 单行子查询 、多行子查询、单行函数、聚合函数 IN 、ANY 、SOME 、ALL
单行子查询 子查询结果是 一个列一行记录 select a,b,c from table where a >(select avg(xx) from table ) 还支持这种写法,这种比较少见 select a,b,c from table where (a ,b)(select xx,xxx from table where col‘000’ )…...
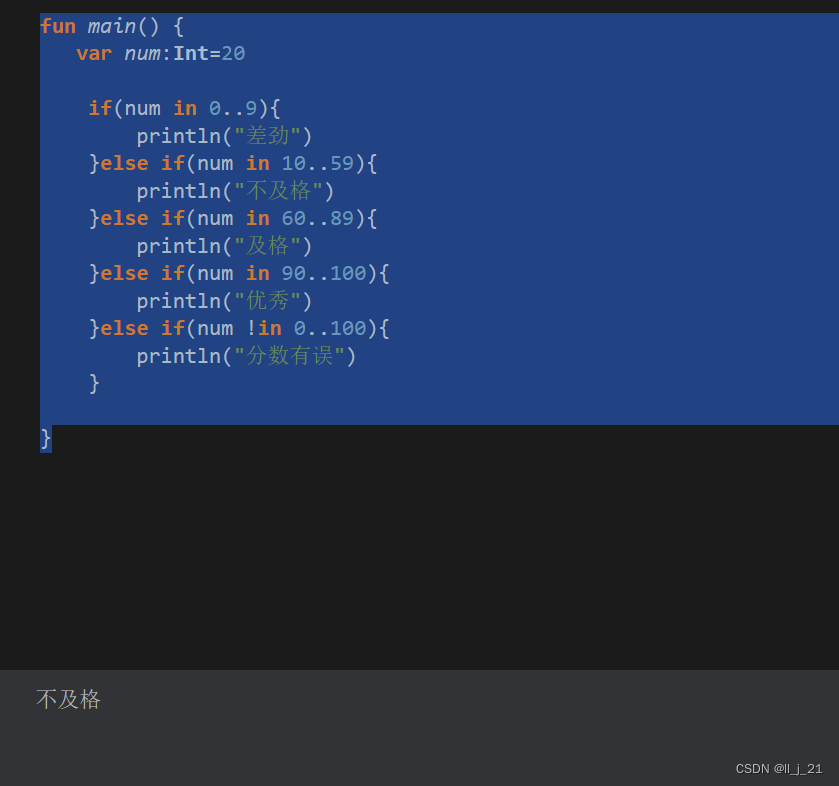
【第一阶段】kotlin的range表达式
range:范围:从哪里到哪里的意思 in:表示在 !in:表示不在 … :表示range表达式 代码示例: fun main() {var num:Int20if(num in 0..9){println("差劲")}else if(num in 10..59){println("不及格")}else if(num in 60..89…...
)
网络防御(5)
一、结合以下问题对当天内容进行总结 1. 什么是恶意软件? 2. 恶意软件有哪些特征? 3. 恶意软件的可分为那几类? 4. 恶意软件的免杀技术有哪些? 5. 反病毒技术有哪些? 6. 反病毒网关的工作原理是什么? 7. 反…...

gradle 命令行单元测试执行问题
文章目录 问题:命令行 执行失败最终解决方案(1)ADB命令(2)Java 环境配置 问题:命令行 执行失败 命令行 执行测试命令 无法使用(之前还能用的。没有任何改动,又不能用了) …...

剑指Offer12.矩阵中的路径 C++
1、题目描述 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平…...

金鸣识别将无表格线的图片转为excel的几个常用方案
我们知道,金鸣识别要将横竖线齐全的表格图片转为excel非常简单,但要是表格线不齐全甚至没有表格线的图片呢?这就没那么容易了,在识别这类图片时,我们一般会使用以下的一种或多种方法进行处理: 1. 基于布局…...

刚刚更新win11,记事本消失怎么处理?你需要注意些什么?
记录window11的bug hello,我是小索奇 昨天索奇从window10更新到了window11,由于版本不兼容卸载了虚拟机,这是第一个令脑壳大的,算了,还是更新吧,了解了解win11的生态,后期重新装虚拟机 第一个可…...

【QT】 QTabWidgetQTabBar控件样式设计(QSS)
很高兴在雪易的CSDN遇见你 ,给你糖糖 欢迎大家加入雪易社区-CSDN社区云 前言 本文分享QT控件QTabWidget&QTabBar的样式设计,介绍两者可以自定义的内容,以及如何定义,希望对各位小伙伴有所帮助! 感谢各位小伙伴…...

【个人记录】CentOS7 编译安装最新版本Git
说明 使用yum install git安装的git版本是1.8,并不是最新版本,使用gitlab-runner托管时候会拉项目失败,这里使用编译源码方式安装最新版本的git。 基础环境安装 echo "nameserver 8.8.8.8" >> /etc/resolv.conf curl -o /…...

【Linux】计算机网络的背景和协议分层
文章目录 网络发展协议何为协议网络协议协议分层OSI七层模型TCP/IP五层模型(四层) 基本通信流程mac地址和ip地址网络通信本质 网络发展 从一开始计算机作为一台台单机使用,到现在网络飞速发展,从局域网Lan建立起局域网࿰…...

代理模式:静态代理+JDK/CGLIB 动态代理
文章目录 1. 代理模式2. 静态代理3. 动态代理3.1. JDK 动态代理机制3.1.1. 介绍 3.1.2. JDK 动态代理类使用步骤3.1.3. 代码示例3.2. CGLIB 动态代理机制3.2.1. 介绍3.2.2. CGLIB 动态代理类使用步骤3.2.3. 代码示例 3.3. JDK 动态代理和 CGLIB 动态代理对比 4. 静态代理和动态…...

gps虚拟定位 AnyGo for Mac 中文
要在AnyGo中进行Gps位置模拟,您只需连接您的设备并选择“位置模拟”选项,然后输入您想要模拟的位置信息即可。通过使用AnyGo,您可以轻松地模拟任何地方的位置,而无需实际去到那个地方。 借助AnyGo,您可以通过在地图上…...

LLM reasoners 入门实验 24点游戏
LLM reasoners Ber666/llm-reasoners 实验过程 实验样例24games,examples/tot_game24,在inference.py中配置使用代理和open ai的api key。 首先安装依赖 git clone https://github.com/Ber666/llm-reasoners cd llm-reasoners pip install -e .然后…...

【LeetCode 算法】Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值-前缀和
文章目录 Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值问题描述:分析代码前缀和前缀和 Tag Maximum Absolute Sum of Any Subarray 任意子数组和的绝对值的最大值 问题描述: 给你一个整数数组 nums 。一个子数组 [ n u m s l ,…...

怎么建立大型语言模型
建立大型语言模型通常涉及以下主要步骤: 数据收集:收集大规模的文本数据作为模型的训练数据。可以从各种来源获取数据,如互联网、书籍、新闻文章等。数据的质量和多样性对于模型的性能至关重要。 数据预处理:对收集到的数据进行预…...

docker简介和安装
什么是docker? docker是基于Go语言编写的开源容器引擎,是操作系统级别的轻量级虚拟技术。主要用于应用打包、分发、部署。 打包:软件开发过程中,打包是将程序打包成软件包或者镜像的过程;在容器化程序中,打…...

记录问题: servlet获取项目包绝对路径
【2023-8-8 23:46:27 星期二】 如何获取在webapp下的路径?而不是target包下的webapp目录 比如这里应该获取到 F:\Tiam\Desktop\freemarker\freemarker-demo01\src\main\webapp 而readPath总是获取到 F:\Tiam\Desktop\freemarker\freemarker-demo01\target\freemarker-demo0…...

C语言文件操作基本方法
1、文件的分类 ANSI C 的缓冲文件系统 缓冲文件系统 缓冲文件系统是指,系统自动地在内存区为每个正在使用的文件开辟一个缓冲区。 从内存向磁盘输出数据时,必须首先输出到缓冲区中。待缓冲区装满后,再一起输出到磁盘文件中。 从磁盘文件向内…...

SQL 相关子查询 和 不相关子查询、Exists 、Not Exists、 多表连接(包含自连接)
不相关子查询 子查询的查询条件不依赖于父查询,称不相关子查询。子查询可以单独运行的 select stu_id,sex,age from student t where sex(select sexfrom studentwhere stu_id10023 )相关子查询 关联子查询 子查询的查询条件依赖于父查询,称为 相关子…...
)
项目规范 编写规范(范例)
项目目录 目录接口参考 项目目录结构设计,增加部分领域模型后缀强制定义,方便统一编码风格。 controller:请求处理 RestController module:按大业务区分,对多个业务对象数据聚合处理 Component manager:…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
