Codeforces の 动态规划
Codeforces Round 785 (Div. 2) - C. Palindrome Basis
dp(9/100)
题目链接
思路:整数划分基础上加一个判断回文的条件
整数划分思路:背包容量为n,物品有体积为1~n n种,每种无数个,求使背包恰好装满的方案数——完全背包问题(传统的背包问题可能不会恰好装满,但此问题中如果背包有空余可以用1补齐,所以是一定会装满的)
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
const int mod = 1e9 + 7;
const int N = 4e4 + 5;
int f[N];void solve()
{ int n;cin >> n;cout << f[n] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;cin >> t;f[0] = 1;for (int i = 1; i <= 4e4; i ++ ){string a = to_string(i);string b = a;reverse(a.begin(), a.end());if(a == b)for (int j = i; j <= 4e4; j ++ )f[j] = (f[j] + f[j - i]) % mod; }while(t -- ) solve(); system("pause");return 0;
}
Codeforces Round 113 (Div. 2) - E. Tetrahedron
dp(18/100)
题目链接
走n步的路线数是走n-2步的三倍加上走n-1步的两倍
当走到n-2步到达D点时,还可向A B C三个方向走一来一回
例如:
f[0] = 1(没有走动,就在原点)路线:D
f[2] 路线就有:
D - A - D;
D - B - D
D - C - D
走到n-1步到达D点的情况,可在当前步向除D以外的另外两点走一步再回到D。
例如:
f[3] 路线有:
D - A - B - D
D - A - C - D
D - B - A - D
D - B - C -D
D - C - A - D
D - C- B - D
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e7 + 10, mod = 1e9 + 7;
int f[N];void solve()
{int n;cin >> n;f[0] = 1;f[1] = 0;for (int i = 2; i <= n; i ++ )f[i] = (2 * f[i - 1] + 3 * f[i - 2]) % mod;cout << f[n] << endl;
}signed main()
{int t = 1;// cin >> t;while(t -- ) solve();return 0;
}
相关文章:

Codeforces の 动态规划
Codeforces Round 785 (Div. 2) - C. Palindrome Basis dp(9/100) 题目链接 思路:整数划分基础上加一个判断回文的条件 整数划分思路:背包容量为n,物品有体积为1~n n种,每种无数个,求使背包恰好装满的方案数——完全背…...
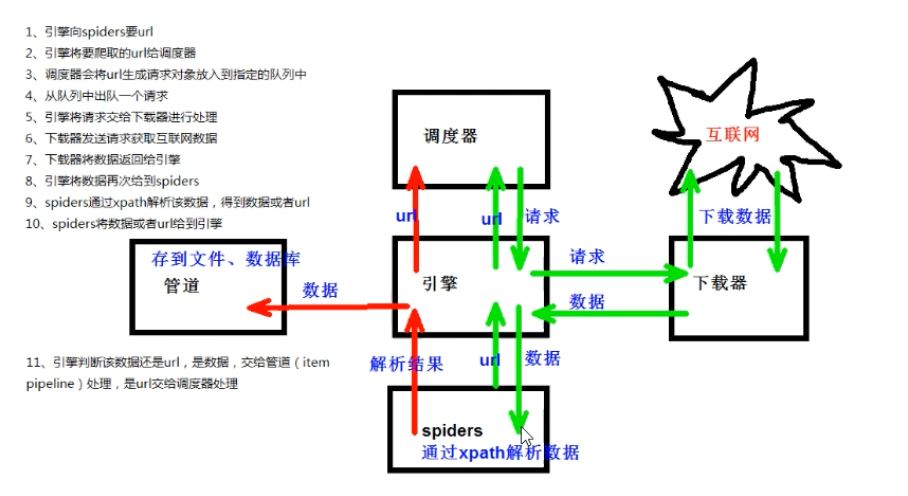
数学建模-爬虫系统学习
尚硅谷Python爬虫教程小白零基础速通(含python基础爬虫案例) 内容包括:Python基础、Urllib、解析(xpath、jsonpath、beautiful)、requests、selenium、Scrapy框架 python基础 进阶(字符串 列表 元组 字典…...
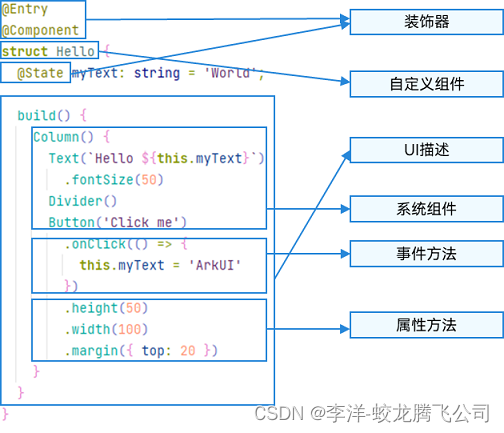
HarmonyOS/OpenHarmony应用开发-ArkTS语言渲染控制概述
ArkUI通过自定义组件的build()函数和builder装饰器中的声明式UI描述语句构建相应的UI。 在声明式描述语句中开发者除了使用系统组件外,还可以使用渲染控制语句来辅助UI的构建,这些渲染控制语句包括控制组件是否显示的条件渲染语句,基于数组数…...

【力扣刷题 | 第二十五天】
目录 前言: 474. 一和零 - 力扣(LeetCode) 总结: 前言: 今天我们依旧暴打动态规划 474. 一和零 - 力扣(LeetCode) 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集…...
GO学习之 函数(Function)
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 文章目录 GO系列前言一、什么是…...

Jstack线上问题排查
1.top查找出哪个进程消耗的cpu高。执行top命令,默认是进程视图,其中PID是进程号(记下进程号) 2.top中shifth 或“H”查找出哪个线程消耗的cpu高 (记下最高的几个线程号) jstack 进程号 >> pid-cpu.…...
VIM 编辑器: Bram Moolenaar
VIM 用了很长时间, 个人的 VIM 配置文件差不多10年没有更新了。以前写程序的时候, 编辑都用这个。 linux kernel, boost规模的代码都不在话下。现在虽然代码写的少了,依然是我打开文件的首选。 现在用手机了,配个蓝牙键…...

鸿蒙应用开发指南:从零开始构建一款智能音乐播放器
介绍 随着鸿蒙操作系统的发布,开发者们迫不及待地想要探索鸿蒙应用的开发。本篇博客将以构建一款智能音乐播放器为例,带你一步步了解鸿蒙应用开发的技术要点和实践。我们将使用HarmonyOS的开发环境和MarkDown进行排版,方便你快速上手。 准备…...
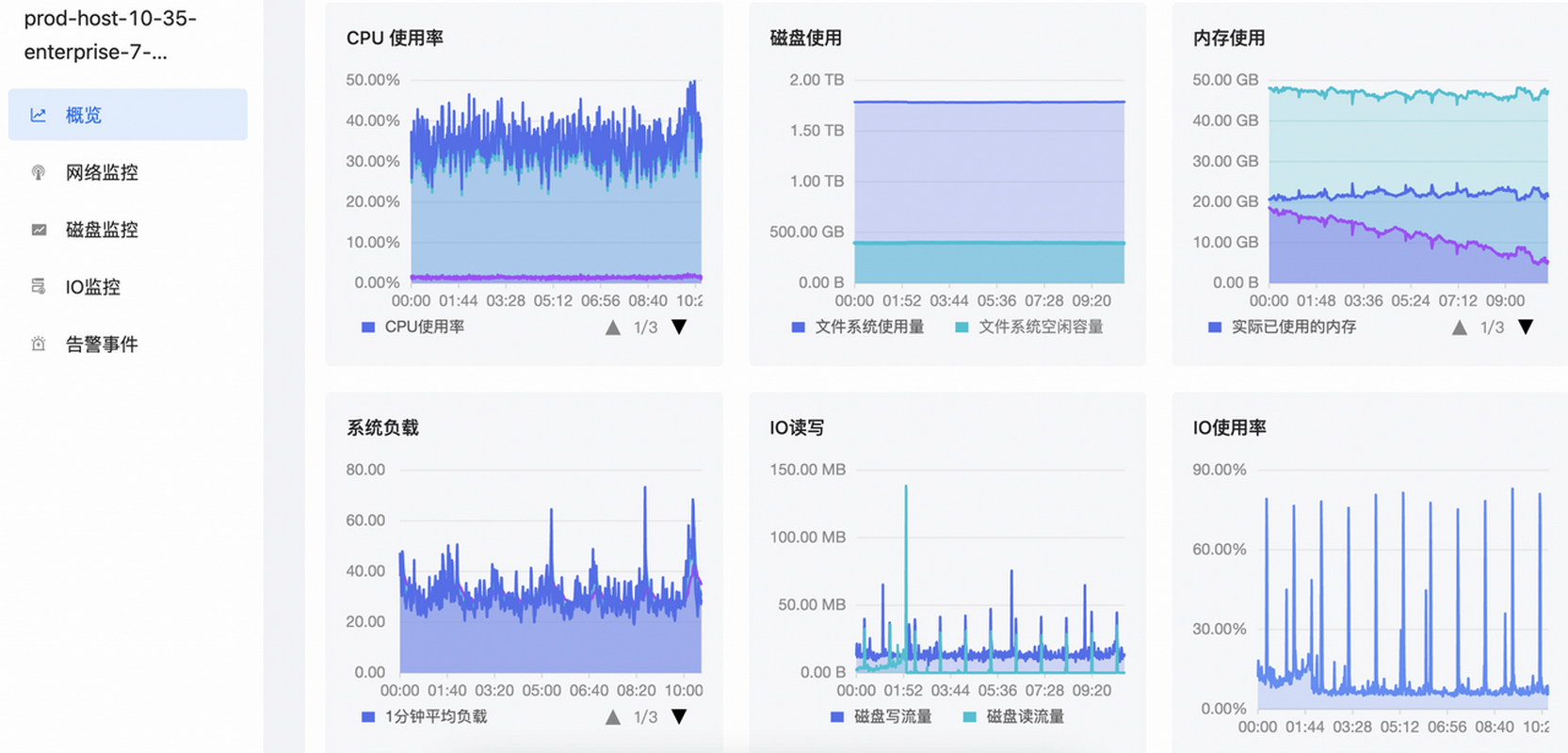
如何实现对主机的立体监控?
主机监控是保证系统稳定性和性能的重要环节之一,那应该如何实现对主机的立体监控? 本期EasyOps产品使用最佳实践,我们将为您揭晓: 主机应该如何分组和管理? 主机监控应该关注哪些关键性指标? 背 景 通…...
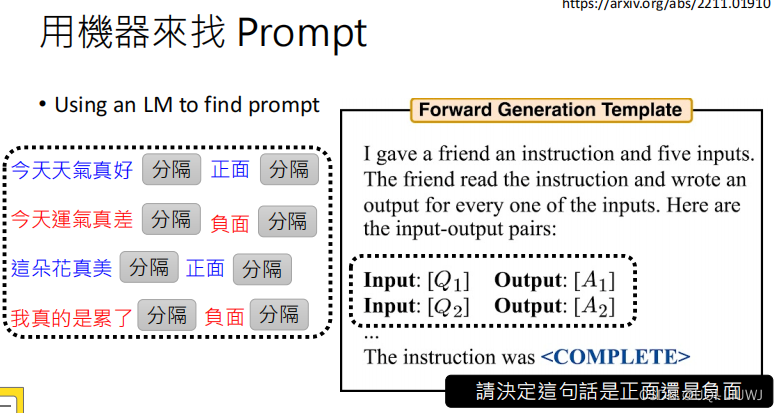
机器学习笔记:李宏毅ChatGPT Finetune VS Prompt
1 两种大语言模型:GPT VS BERT 2 对于大语言模型的两种不同期待 2.1 “专才” 2.1.1 成为专才的好处 Is ChatGPT A Good Translator? A Preliminary Study 2023 Arxiv 箭头方向指的是从哪个方向往哪个方向翻译 表格里面的数值越大表示翻译的越好 可以发现专门做翻…...
)
中电金信:逐数兴业 智启未来——“数据二十条”影响之解读 (下)
在逐数兴业 智启未来——“数据二十条”影响之解读(上)篇内容中,主要解读了有关于“数据二十条”发布的背景与意义、建立数据要素市场面临的挑战与应对。在今天的文章里,将继续解读“数据二十条”的主要内容以及对金融行业和金融科…...

54款宝藏级AIGC工具分享(claude,Midjourney,Stable Diffusion等)
随着ChatGPT的一波又一波高潮,生成式AI逐渐进入人们视野,并开始大行其道,正如人们所说:AI用的好,天天下班早! 当然,有效的利用AI不但能下班早,还能在上班时间摸鱼,就如潘…...
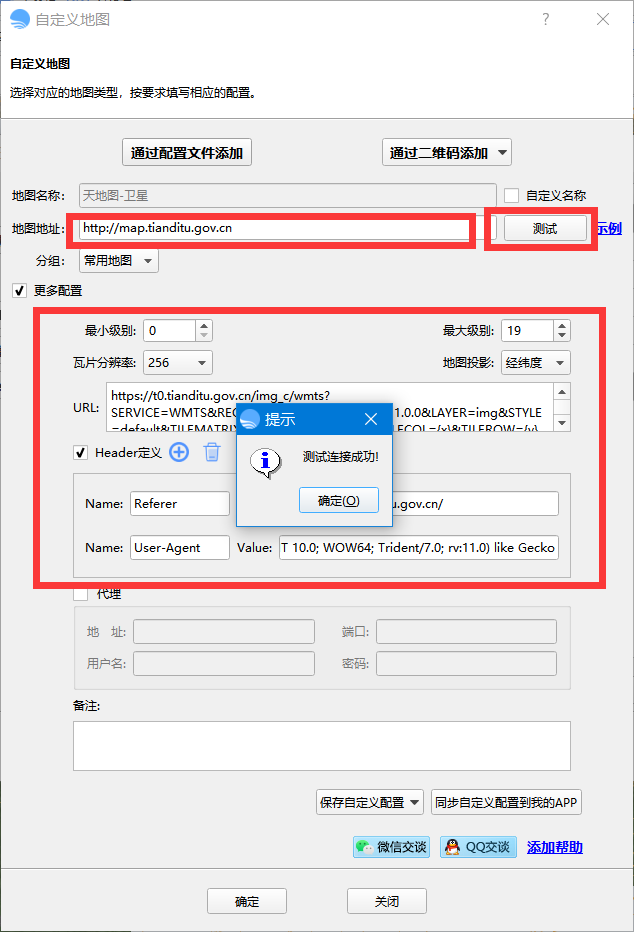
bigemap如何添加在线地图源?
第一步 打开浏览器,找到你要访问的地图的URL地址,并且确认可以正常在浏览器中访问;浏览器中不能访问,同样也不能在软件中访问。 以下为常用地图源地址: 天地图: http://map.tianditu.gov.cn 包含&a…...
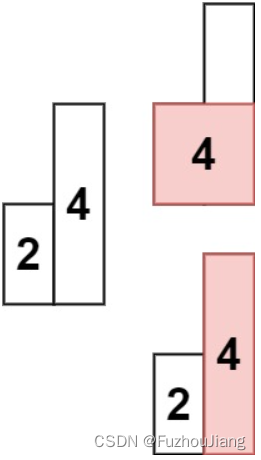
84. 柱状图中最大的矩形
题目描述 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。 求在该柱状图中,能够勾勒出来的矩形的最大面积。 示例 1: 输入:heights [2,1,5,6,2,3] 输出:10 解释:最…...

嘉楠勘智k230开发板上手记录(二)--hello world
上次成功在k230上烧录sdk,这次准备实现hello world和ssh scp远程k230 主要是按照K230 SDK 基础教程的K230_实战基础篇_hello_world.md 一、PC连接k230 1. 初步准备 首先下载串口工具PuTTY,这个我个人感觉比较方便。 准备两根USB type-C数据线&#…...
ArcGIS Pro实践技术应用——暨基础入门、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合、案例应用全流程科研能力提升
查看原文>>>ArcGIS Pro实践技术应用——暨基础入门、制图、空间分析、影像分析、三维建模、空间统计分析与建模、python融合能力 本文将利用ArcGIS Pro 将您的 GIS 工作组织到工程中,您可以使用 ArcGIS Pro 映射 2D 和 3D 数据。借助 ArcGIS Proÿ…...

学习pytorch
学习pytorch 1. 环境安装配置镜像源conda命令记录图像相关代码遇到的问题1. torch.cuda.is_available() False 1. 环境安装 B站小土堆视频 配置镜像源 conda config --show channels conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/main…...

动态SQL实现原理一-动态SQL的使用
在介绍MyBatis动态SQL实现原理之前,我们先来了解一下MyBatis动态SQL的使用。顾名思义,动态SQL指的是事先无法预知具体的条件,需要在运行时根据具体的情况动态地生成SQL语句。 假设我们有一个获取用户信息查询操作,具体的查询条件…...
MyBatis动态sql标签帮你轻松搞定sql拼接
动态sql介绍 由于在开发过程不同的业务中会用到不同的操作条件,如果每个业务都拼接不同sql语句的话会是一个庞大的工作量;此时动态sql就能解决这个问题,可以针对不确定的操作条件动态拼接sql语句,根据提交的条件来完成业务sql的执…...
Java课题笔记~ 使用 Spring 的事务注解管理事务(掌握)
通过Transactional 注解方式,可将事务织入到相应 public 方法中,实现事务管理。 Transactional 的所有可选属性如下所示: propagation:用于设置事务传播属性。该属性类型为 Propagation 枚举, 默认值为 Propagation.R…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
