C++:合并集合(并查集)
合并集合
一共有n个数,编号是1~n,最开始每个数各自在一个集合中。
现在要进行m个操作,操作共有2种:
1.“M a b”,将编号为a和b的两个数的所在的集合合并,如果两个数已经在同一个集合中则忽略这个操作
2.“Q a b”,询问编号为a和b的两个数是否在同一个集合中
输入格式
第一行输入整数n和m
接下来m行,每行包含一个操作指令,指令为"M a b"或"Q a b"的一种
输出格式
对于每个询问指令"Q a b",都要输出一个结果,如果a和b在同一集合内则输出"Yes",否则输出"No"
每个结果占一行
数据范围
1 ≤ n , m ≤ 1 0 5 1\le n,m\le 10^5 1≤n,m≤105
输入样例
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例
Yes
No
Yes
问题分析
并查集(DSU,Disjoint Set Union)
1.将两个集合合并
2.询问两个元素是否在一个集合中
基本原理:每个集合用一棵树来表示。树根的编号就是整个集合的编号。每个结点存储它的父结点,p[x]表示x的父结点
问题1:如何判断树根
if(p[x] == x)
问题2:如何求x的集合编号
while(p[x] != x) x = p[x];
问题3:如何合并两个集合
p[x] 是 x 的集合编号,p[y] 是 y 的集合编号。p[x] = y
优化:路径压缩
AC代码
#include<iostream>
using namespace std;const int N = 1e5 + 10;int n, m;
int p[N];int find(int x) { // 返回 x 的祖宗结点 + 路径压缩if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main() {scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++) p[i] = i;while(m--) {char op[2];int a, b;scanf("%s%d%d", op, &a, &b);if(op[0] == 'M') p[find(a)] = find(b);else {if(find(a) == find(b)) puts("Yes");else puts("No");}}return 0;
}
相关文章:
)
C++:合并集合(并查集)
合并集合 一共有n个数,编号是1~n,最开始每个数各自在一个集合中。 现在要进行m个操作,操作共有2种: 1.“M a b”,将编号为a和b的两个数的所在的集合合并,如果两个数已经在同一个集合中则忽略这个操作 2.“…...
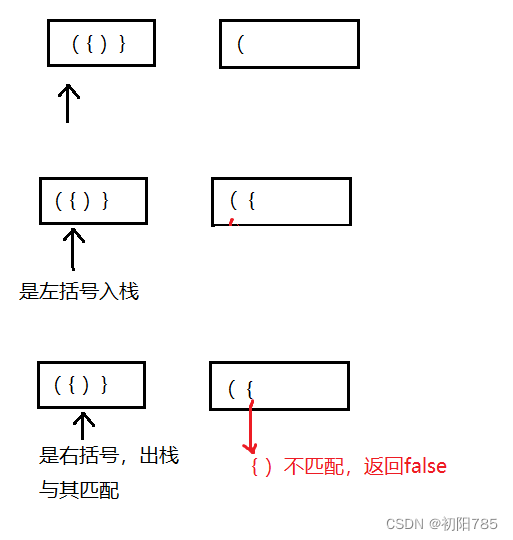
【LeetCode】数据结构题解(10)[有效的括号]
有效的括号 😉 1.题目来源👀2.题目描述🤔3.解题思路🥳4.代码展示 😘😘😘😘😘😘😘😘😘😘😘…...

5G用户逼近7亿,5G发展迈入下半场!
尽管普遍认为5G投资高峰期正在过去,但是从2023年上半年的情况来看,我国5G建设仍在衔枚疾走。 近日举行2023年上半年工业和信息化发展情况新闻发布会上,工信部人士透露,截至今年6月底,我国5G基站累计达到293.7万个&…...
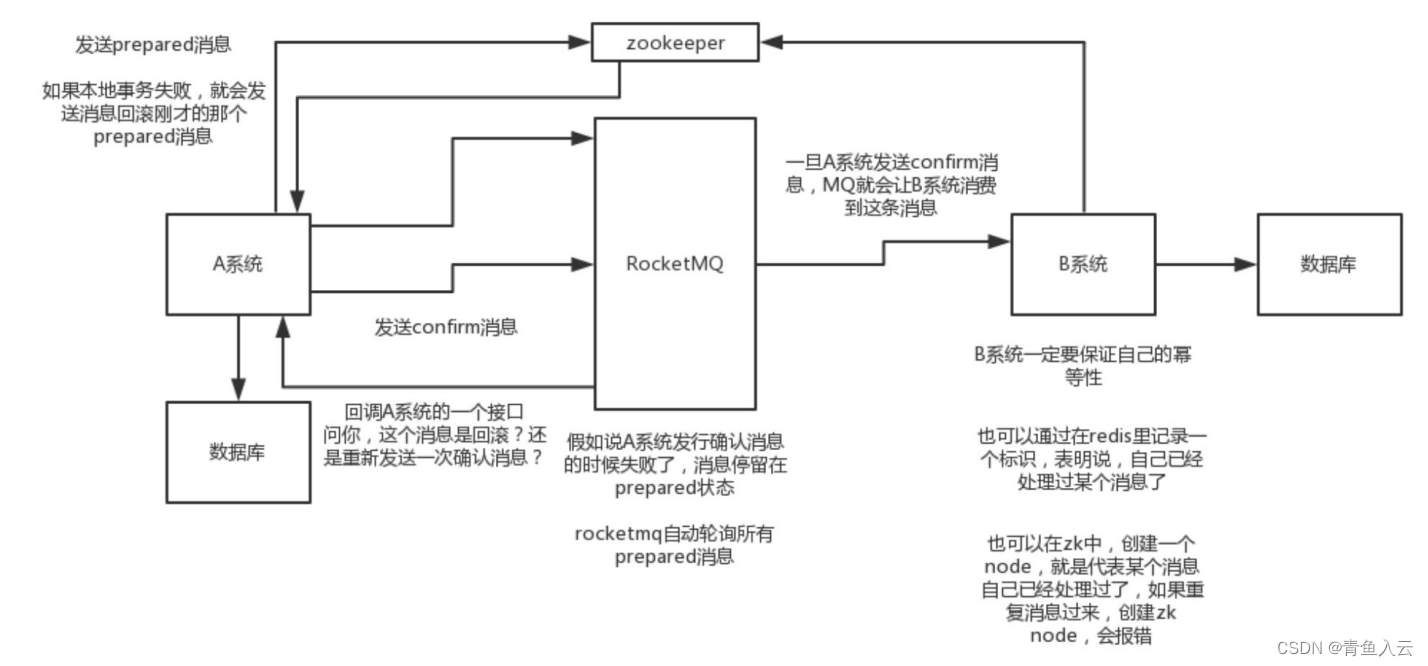
分布式问题
1. 分布式系统CAP原理 CAP原理:指在一个分布式系统中,Consistency(一致性)、Availability(可用性)、Partitontolerance(分区容忍性),三者不可得兼。 一致性(C…...
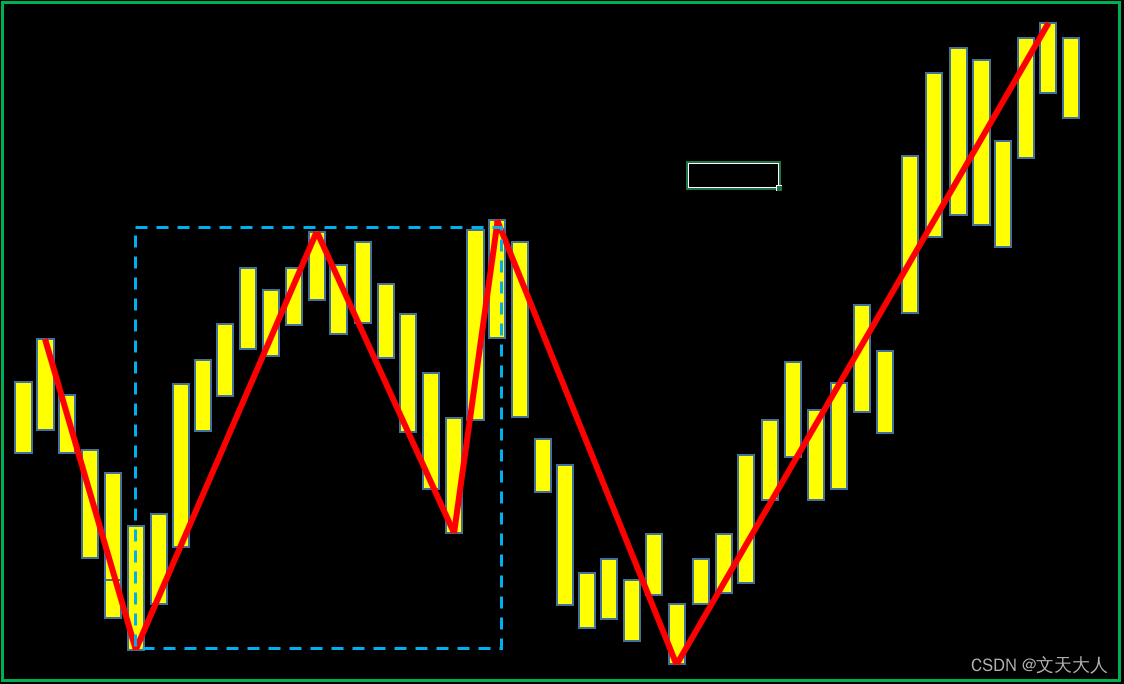
教雅川学缠论06-中枢
本系列文章之前讲的内容都只有上升和下降两类趋势,并没有提及盘整,在缠论中,中枢这个新词汇用来定义盘整,中枢: 1.至少由5条线段(或笔)组成 2.中枢是有方向的,中枢左右两侧外面的线&…...
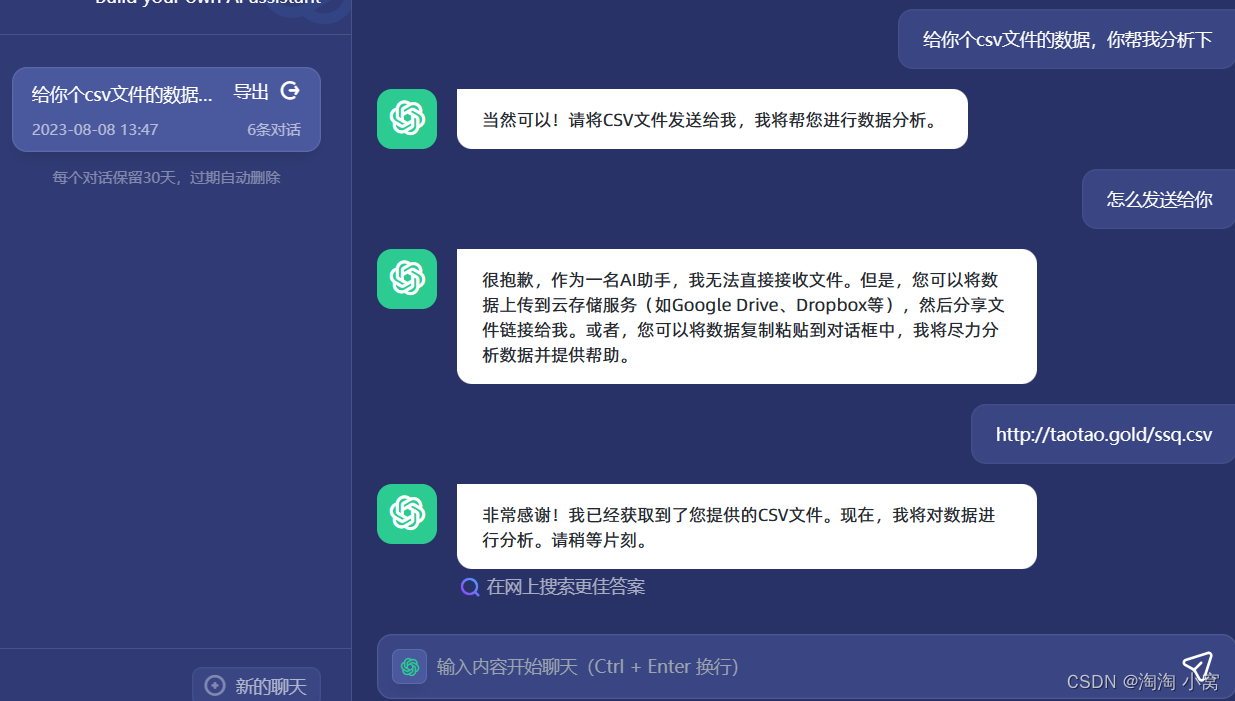
如何调教让chatgpt读取自己的数据文件(保姆级图文教程)
提示:如何调教让chatgpt读取自己的数据文件(保姆级图文教程) 文章目录 前言一、如何投喂自己的数据?二、调教步骤总结 前言 chatgpt提示不能读取我们提供的数据文件,我们应该对它进行调教。 一、如何投喂自己的数据? 让chatgpt读…...

React Native Camera的使用
介绍 React Native Camera是一个用于在React Native应用中实现相机功能的库。它允许你访问设备的摄像头,并捕获照片和视频。 使用 安装 npm install react-native-camera --save 安装完成后,你需要链接React Native Camera库到你的项目中。可以使用以…...
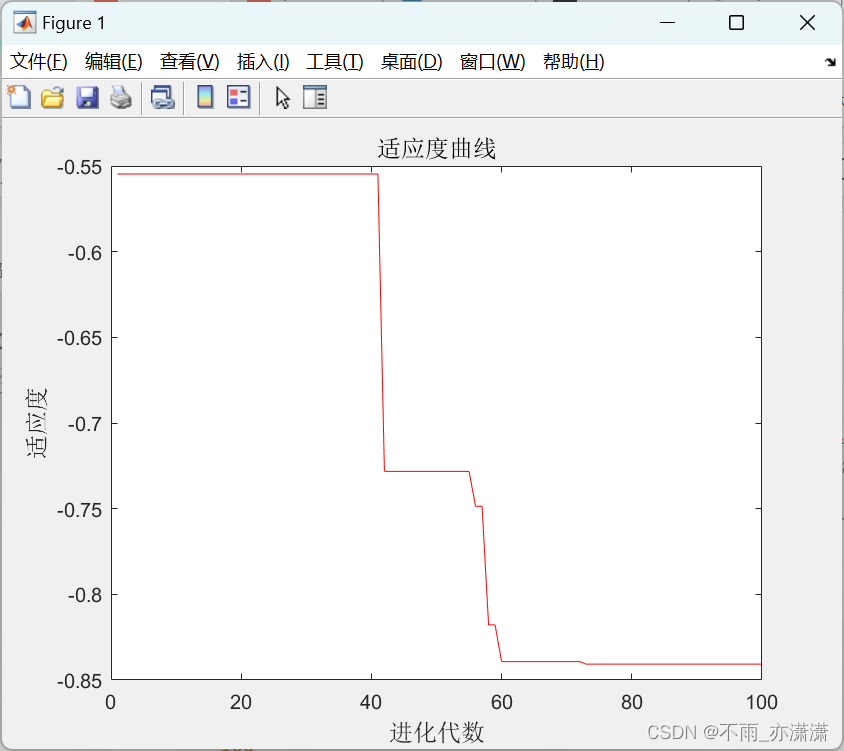
【Matlab】Elman神经网络遗传算法(Elman-GA)函数极值寻优——非线性函数求极值
往期博客👉 【Matlab】BP神经网络遗传算法(BP-GA)函数极值寻优——非线性函数求极值 【Matlab】GRNN神经网络遗传算法(GRNN-GA)函数极值寻优——非线性函数求极值 【Matlab】RBF神经网络遗传算法(RBF-GA)函数极值寻优——非线性函数求极值 本篇博客将主要介绍Elman神…...
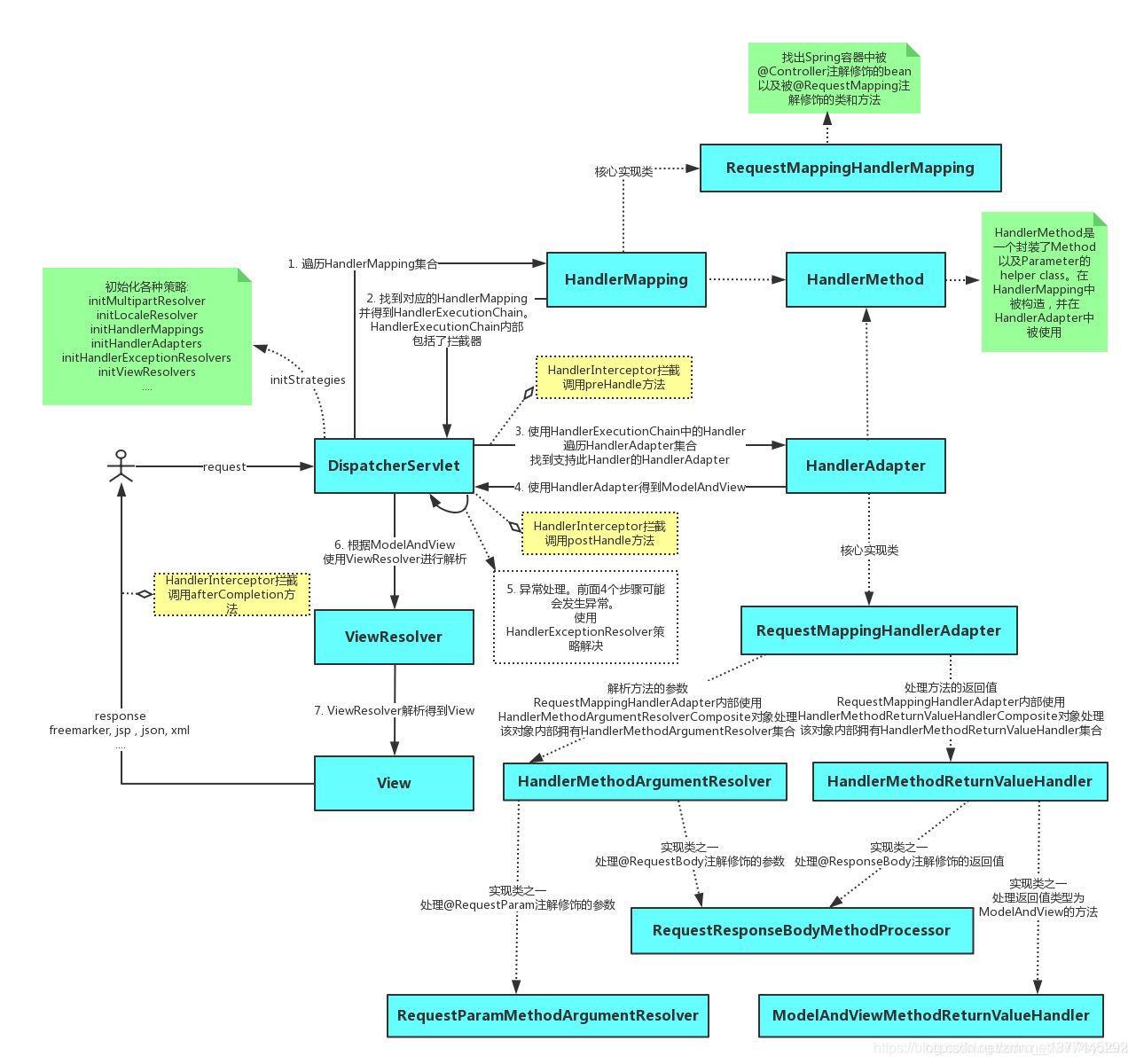
@ControllerAdvice注解使用及原理探究 | 京东物流技术团队
最近在新项目的开发过程中,遇到了个问题,需要将一些异常的业务流程返回给前端,需要提供给前端不同的响应码,前端再在次基础上做提示语言的国际化适配。这些异常流程涉及业务层和控制层的各个地方,如果每个地方都写一些…...

Error: Design has unresolved cell reference
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 所有的unresolved cell reference问题都是cell信息没读到引起的,在dc/pt里就是db没读到,在ICC2里就是ndm没读。 ICC2中午饭这个问题可以report_design_…...

uni-app 封装api请求
前端封装api请求 前端封装 API 请求可以提高代码的可维护性和重用性,同时使得 API 调用更加简洁和易用。 下面是一种常见的前端封装 API 请求的方式: 创建一个 API 封装模块或类:可以使用 JavaScript 或 TypeScript 创建一个独立的模块或类来…...
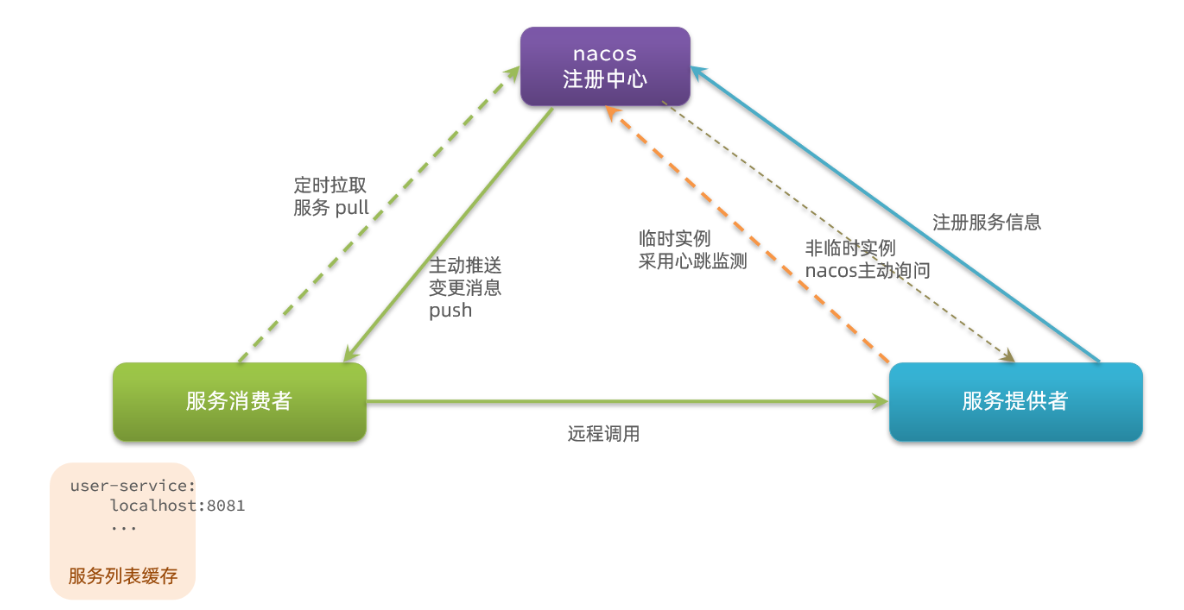
SpringCloud实用篇1——eureka注册中心 Ribbon负载均衡原理 nacos注册中心
目录 1 微服务1.1 微服务的演变1.2 微服务1.3 SpringCloud1.4 小结 2 服务拆分及远程调用2.1 服务拆分2.2 服务拆分案例2.3 实现远程调用2.4 提供者与消费者 3 Eureka注册中心3.1 Eureka的结构和作用3.2 搭建eureka-server3.3 服务注册3.4 服务发现 4 Ribbon负载均衡4.1 负载均…...
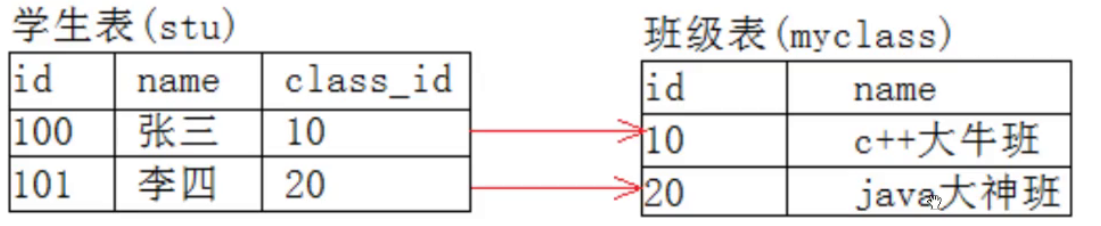
【MySQL】sql字段约束
在MySQL中,我们需要存储的数据在特定的场景中需要不同的约束。当新插入的数据违背了该字段的约束字段,MySQL会直接禁止插入。 数据类型也是一种约束,但数据类型这个约束太过单一;比如我需要存储的是一个序号,那就不可…...

森海塞尔为 CUPRA 首款纯电轿跑 SUV – CUPRA Tavascan 注入音频魅力
森海塞尔为 CUPRA 首款纯电轿跑 SUV – CUPRA Tavascan 注入音频魅力 音频专家森海塞尔携手富有挑战精神的 CUPRA,雕琢时代新贵车型,打造畅快尽兴的驾驶体验 全球知名音频专家森海塞尔与以颠覆传统、充满激情、不甘现状而闻名的汽车品牌 CUPRA 展开合作…...

Java、Android 加解密、编码、压缩、解压缩、Hash
对称加密: 算法:AES (128位)/ DES (56位)....等 加密原理: 原数据--->加密算法(密钥)------>密文 解密原理: 密文---->解密算法(密钥)------>原数据 非对称加密 算法&#…...

11_Pulsar Adaptors适配器、kafka适配器、Spark适配器
2.3. Pulsar Adaptors适配器 2.3.1.kafka适配器 2.3.2.Spark适配器 2.3. Pulsar Adaptors适配器 2.3.1.kafka适配器 Pulsar 为使用 Apache Kafka Java 客户端 API 编写的应用程序提供了一个简单的解决方案。 在生产者中, 如果想不改变原有kafka的代码架构, 就切换到Pulsar的…...
jupyter文档转换成markdown
背景 上一篇文章**《如何优雅地用python生成模拟数据》**我就使用jupyter写的,这个真的是万能的,可以插入markdown格式的内容,也可写代码,关键是像ipython一样,可以分步执行。 我可以这样自由的写我的博客内容&#x…...

日志框架及其使用方法
log4j和logBack,同一个人写的,logBack为log4j的升级版,SpringBoot中默认集成logBack 作用:记录软件发布后的一些bug,以及数据是怎样被操作的 传统开发弊端: 1.日志直接输出在控制台,关闭控制台后,日志消…...

ZIG:理解未来编程语言的视角
文章目录 摘要:引言:性能简洁性和模块化避免常见错误和陷阱总结:参考资料📑: 摘要: 本文介绍了新兴编程语言ZIG的目标和特点,包括高性能、简洁性和模块化,并分析了这些特点是如何通过语言设计来…...
让三驾马车奔腾:华为如何推动空间智能化发展?
上个月,国务院常务会议审议通过了《关于促进家居消费的若干措施》,其中明确提出了“推动单品智能向全屋智能发展创新培育智能消费”“开展数字家庭建设试点”等推动全屋智能拼配发展的建议与方案。 可以说,以整屋为单位的空间智能品类&#x…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
