海外直播种草短视频购物网站巴西独立站搭建
一、市场调研
在搭建网站之前,需要进行充分的市场调研,了解巴西市场的消费者需求、购物习惯和竞争情况。可以通过以下途径进行市场调研:
调查问卷:可以在巴西市场上发放调查问卷,了解消费者的购物习惯、偏好、购买力等信息。
网络调研:可以通过搜索引擎、社交媒体等途径,了解巴西市场上类似网站的运营情况、用户评价、竞争情况等。
市场分析:可以通过相关机构或市场分析报告,了解巴西市场的经济、政治、文化等情况。
二、网站搭建
在确定市场调研结果后,可以选择合适的网站搭建平台,注册域名,设置网站主题、页面布局、颜色搭配等。在网站搭建过程中,需要注意以下几点:
网站速度:由于巴西的互联网发展相对滞后,网站速度可能会受到影响,因此需要选择合适的服务器和网络线路,确保网站的速度和稳定性。
用户体验:巴西市场的消费者对于网站的用户体验要求较高,因此需要注重网站的设计、交互、信息架构等方面的优化。
支付方式:需要选择合适的支付方式,如巴西的本地支付方式等,确保支付的便捷和安全。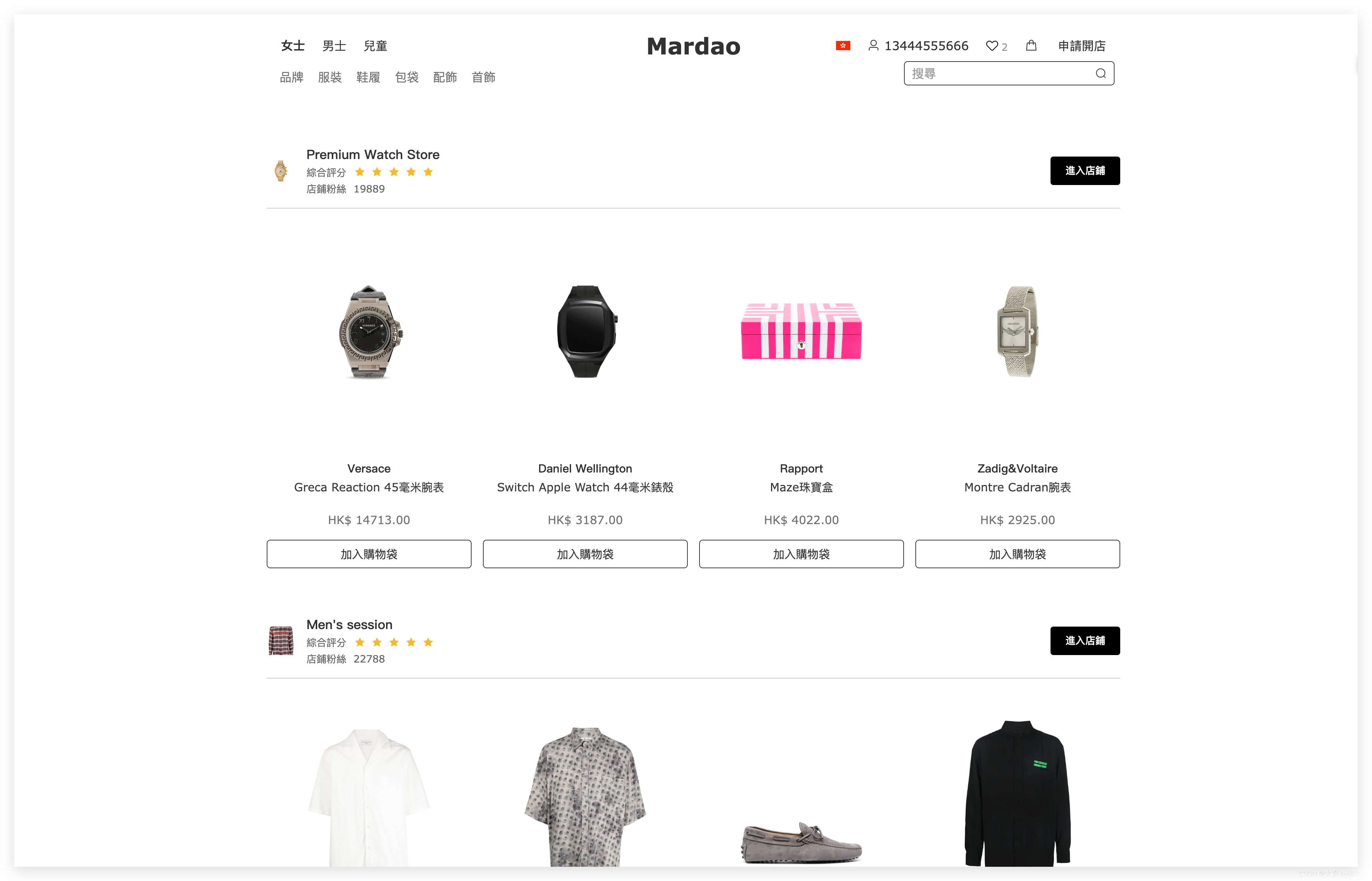
三、直播功能集成
为了满足巴西市场上消费者的需求,需要在网站上集成直播功能。可以选择合适的直播功能插件并将其集成到网站中。在集成过程中,需要注意以下几点:
直播稳定性:需要确保直播的稳定性和流畅性,避免出现卡顿、延迟等问题。
直播互动性:需要提供直播互动功能,如评论、点赞、分享等,增强用户参与感。
直播个性化:需要根据不同的直播内容,提供个性化的直播功能和设置,满足用户多样化的需求。
四、短视频功能集成
为了吸引更多的用户,可以在网站上集成短视频功能。可以选择合适的短视频功能插件,如Lumio等,并将其集成到网站中。在集成过程中,需要注意以下几点:
短视频质量:需要确保短视频的质量和清晰度,避免出现模糊、卡顿等问题。
短视频内容:需要根据不同的产品特点,提供丰富多彩的短视频内容,满足用户多样化的需求。
短视频互动性:需要提供短视频互动功能,如评论、点赞、分享等,增强用户参与感。
五、购物功能集成
为了实现网站的购物功能,可以选择合适的购物功能插件,并将其集成到网站中。在集成过程中,需要注意以下几点:
购物安全性:需要确保购物的安全性,保障用户的支付信息和资金安全。
购物便捷性:需要提供便捷的购物流程和多样化的商品分类,方便用户快速找到所需商品。
购物个性化:需要根据用户的购物历史和偏好,提供个性化的购物推荐和优惠券等,增强用户的购买欲望。
六、本地化优化
针对巴西市场进行本地化优化,包括语言翻译、货币转换、税务计算、支付方式选择等。在本地化优化过程中,需要注意以下几点:
符合当地法规:需要遵守当地的法律法规和相关政策,如巴西的税收法规、数据保护法规等。
贴近当地文化:需要了解当地的文化背景和消费习惯,提供贴近当地文化的产品和服务。
提高当地用户的黏性:需要提供当地用户感兴趣的信息和服务,提高当地用户的黏性和参与度。
七、营销推广
为了吸引更多的潜在用户,需要进行营销推广。可以选择以下几种营销推广方式:
社交媒体推广:可以通过巴西的社交媒体平台,进行广告投放和推广。
网络广告投放:可以通过网络广告平台,进行广告投放和推广。
SEO优化:可以通过搜索引擎优化(SEO),提高网站的搜索排名和曝光率。
在营销推广过程中,需要注意以下几点:
目标用户定位:需要明确目标用户的特点和需求,进行精准营销。
数据跟踪和分析:需要跟踪和分析营销推广的效果和成本,不断优化营销策略。
灵活调整:需要根据市场变化和用户需求的变化,灵活调整营销策略和推广方式。
八、数据分析
通过数据分析工具,对网站流量、用户行为、销售数据进行跟踪和分析,不断优化网站内容和营销策略。在数据分析过程中,需要注意以下几点:
数据跟踪和监测:需要跟踪和监测网站的各种数据指标,如访问量、转化率、跳出率
相关文章:

海外直播种草短视频购物网站巴西独立站搭建
一、市场调研 在搭建网站之前,需要进行充分的市场调研,了解巴西市场的消费者需求、购物习惯和竞争情况。可以通过以下途径进行市场调研: 调查问卷:可以在巴西市场上发放调查问卷,了解消费者的购物习惯、偏好、购买力…...

C#图像均值和方差计算实例
本文展示图像均值和方差计算实例,分别实现RGB图像和8位单通道图像的计算方法 实现代码如下: #region 方法 RGB图像均值 直接操作内存快/// <summary>/// 定义RGB图像均值函数/// </summary>/// <param name="bmp"></param>/// <retur…...

【动态规划】数字三角形
算法提高课课堂笔记。 文章目录 摘花生题意思路代码 最低通行费题意思路代码 方格取数题意思路代码 摘花生 题目链接 Hello Kitty想摘点花生送给她喜欢的米老鼠。 她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。 地里每个道…...

【C++】开源:ceres和g2o非线性优化库配置使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍ceres和g2o非线性优化库配置使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下&…...
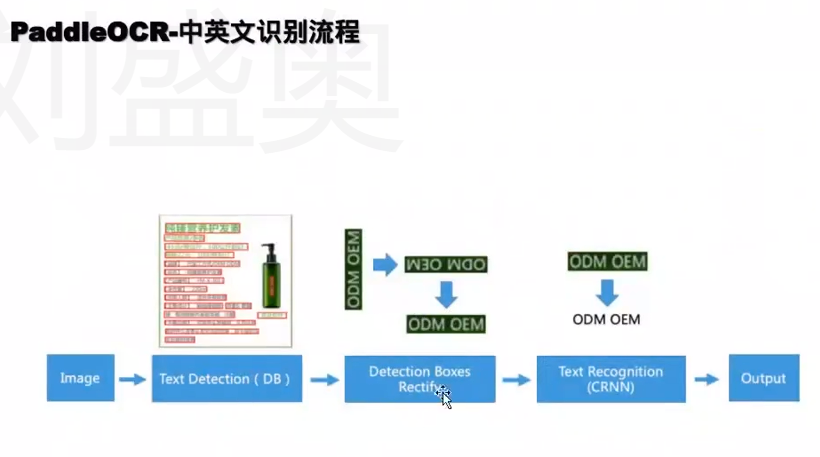
OCR学习
...

《练习100》56~60
题目56 M 5 a [1, 2, 3, 4, 5] i 1 j M - 1 while i < M:# print(f"第{i1}轮交换前:i {i}, j {j} , a[{i}] {a[i]} , a[{j}] {a[j]}")a[i], a[j] a[j], a[i]# print(f"第{i1}轮交换后:i {i}, j {j} , a[{i}] {a[i]} , a[…...
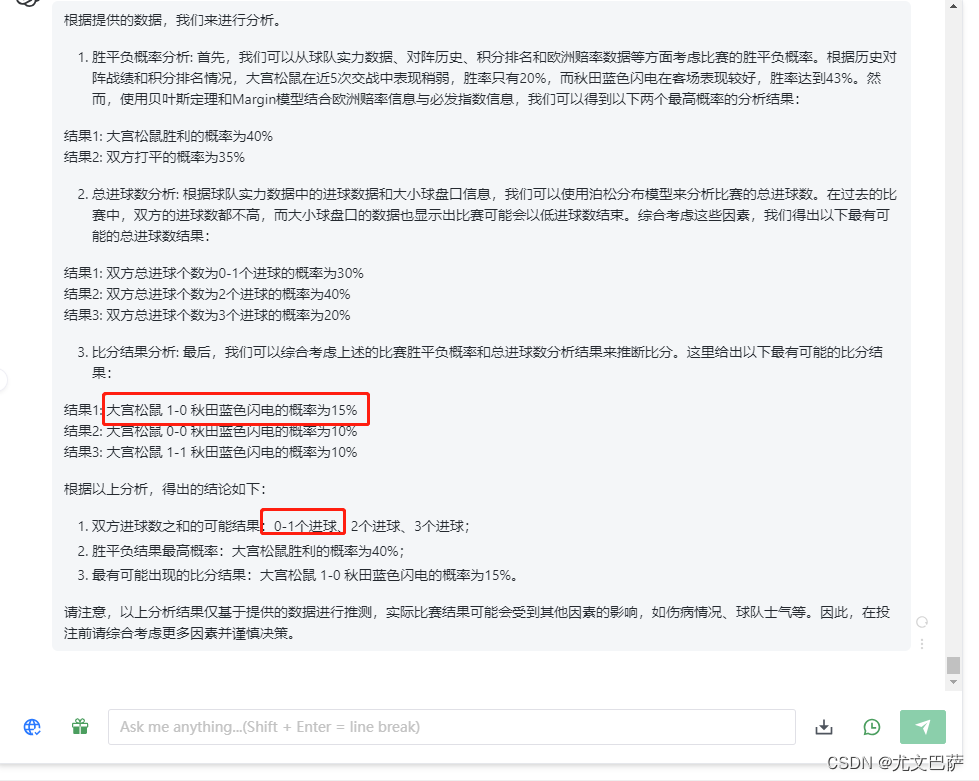
基于大数据为底层好用准确性高的竞彩足球比分预测进球数分析软件介绍推荐
大数据与贝叶斯理论在足球比赛分析与预测中的应用 随着科技的不断进步,大数据分析在各个领域的应用也越来越广泛,其中包括体育竞技。足球比赛作为全球最受欢迎的运动之一,也借助大数据和贝叶斯理论来进行模型分析和预测。本文将通过结合贝叶…...
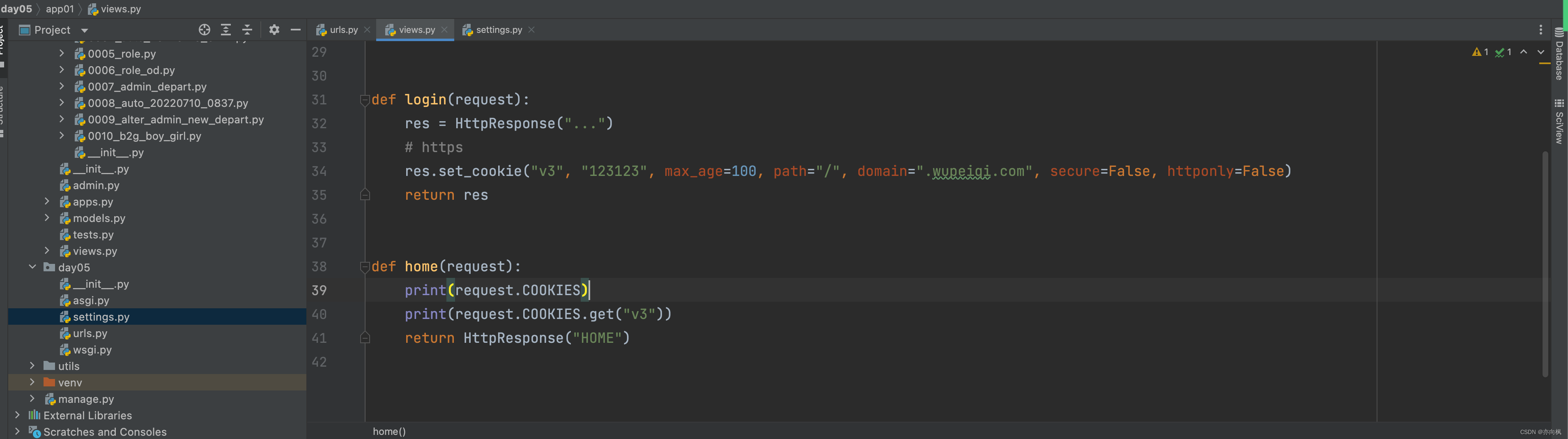
Django进阶
1.orm 1.1 基本操作 orm,关系对象映射。 类 --> SQL --> 表 对象 --> SQL --> 数据特点:开发效率高、执行效率低( 程序写的垃圾SQL )。 编写ORM操作的步骤: settings.py,连…...

Linux系统服务管理
服务命令比较 操作 Linux 6 Linux7 服务开机自动启动 chkconfig --level 35 iptables on systemctl enable firewalld.service 服务器开机不自动启动 chkconfig --level 35 iptables off systemctl disable firewalld.service 加入自定义服务 chkconfig --add aaa s…...
C#之控制台版本得贪吃蛇
贪吃蛇小时候大家都玩过,具体步骤如下: 1.给游戏制造一个有限得空间。 2.生成墙壁,小蛇碰撞到墙壁或者咬到自己的尾巴,游戏结束。 3.生成随机的食物。 4.吃掉食物,增加自身的体长,并生成新的食物。 具体代码如下&…...

ffplay数据结构分析(一)
本文为相关课程的学习记录,相关分析均来源于课程的讲解,主要学习音视频相关的操作,对字幕的处理不做分析 下面我们对ffplay的相关数据结构进行分析,本章主要是对PacketQueue的讲解 struct MyAVPacketList和PacketQueue队列 ffp…...
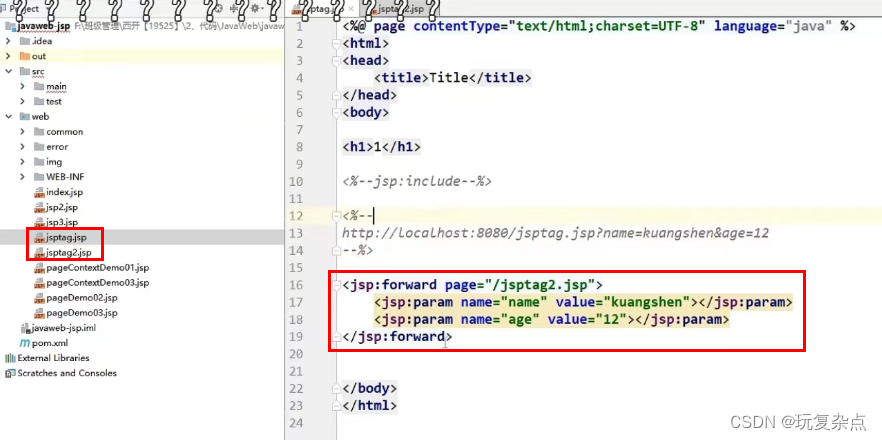
JavaWeb学习|JSP相关内容
1.什么是JSP Java Server Pages: Java服务器端页面,也和Servlet一样,用于动态Web技术! 最大的特点: 。写JSP就像在写HTML 。区别: 。HTML只给用户提供静态的数据 。JSP页面中可以嵌入JAVA代码,为用户提供动态数据 JSP最终也会被转换成为一…...

Springboot后端通过路径映射获取本机图片资源
项目场景: 项目中对图片的处理与查看是必不可少的,本文将讲解如何通过项目路径来获取到本机电脑的图片资源 如图所示,在我的本机D盘的图片测试文件夹(文件夹名字不要有中文)下有一些图片, 我们要在浏览器上访问到这些图片&#…...
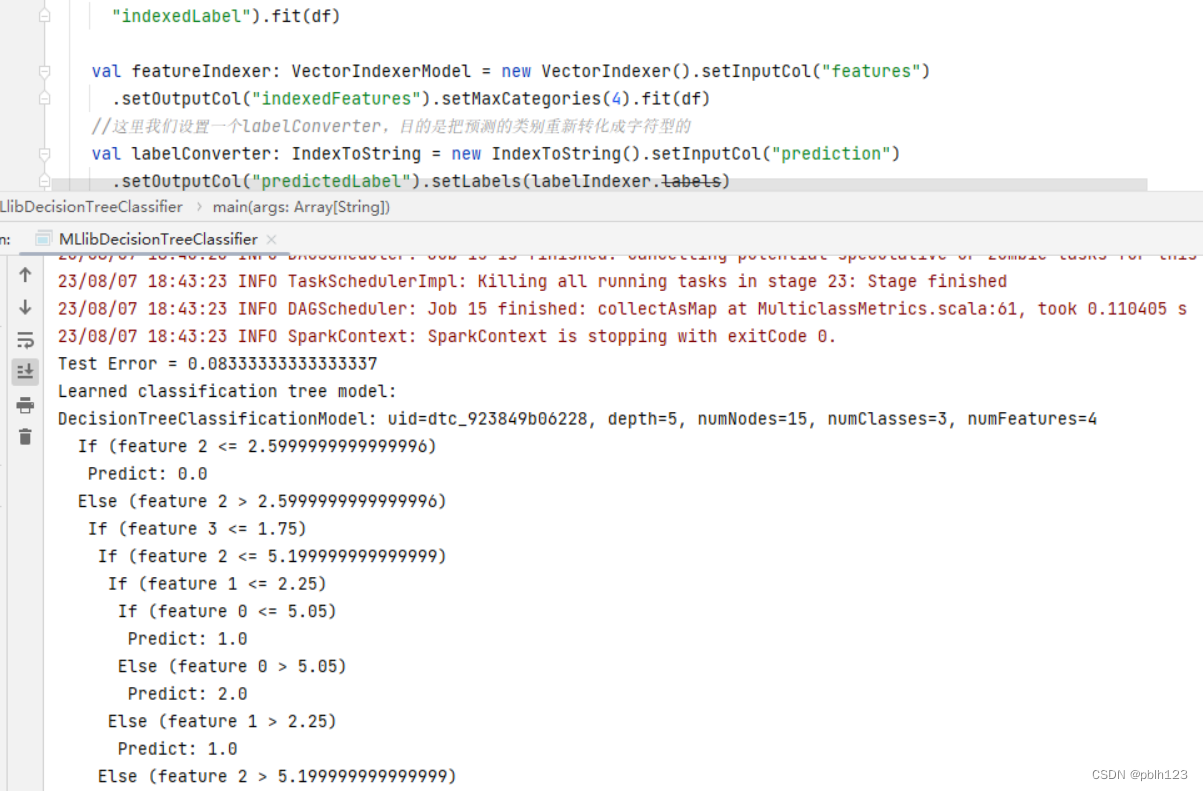
【IDEA + Spark 3.4.1 + sbt 1.9.3 + Spark MLlib 构建鸢尾花决策树分类预测模型】
决策树进行鸢尾花分类的案例 背景说明: 通过IDEA Spark 3.4.1 sbt 1.9.3 Spark MLlib 构建鸢尾花决策树分类预测模型,这是一个分类模型案例,通过该案例,可以快速了解Spark MLlib分类预测模型的使用方法。 依赖 ThisBuild /…...
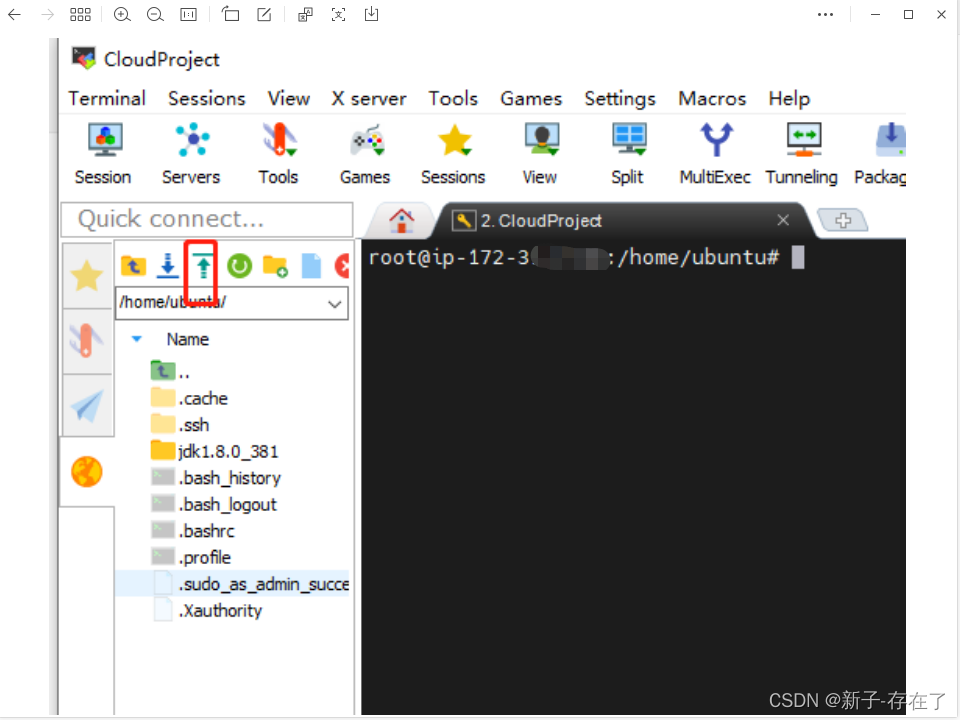
亚马逊 EC2服务器下部署java环境
1. jdk 1.8 安装 1.1 下载jdk包 官网 Java Downloads | Oracle tar.gz 包 下载下来 1.2 本地连接 服务器 我用的是亚马逊的ec2 系统是 ubuntu 的 ssh工具是 Mobaxterm , 公有dns 创建实例时的秘钥 链接 Mobaxterm 因为使用的 ubuntu 所以登录的 名称 就是 ubuntu 然后 …...
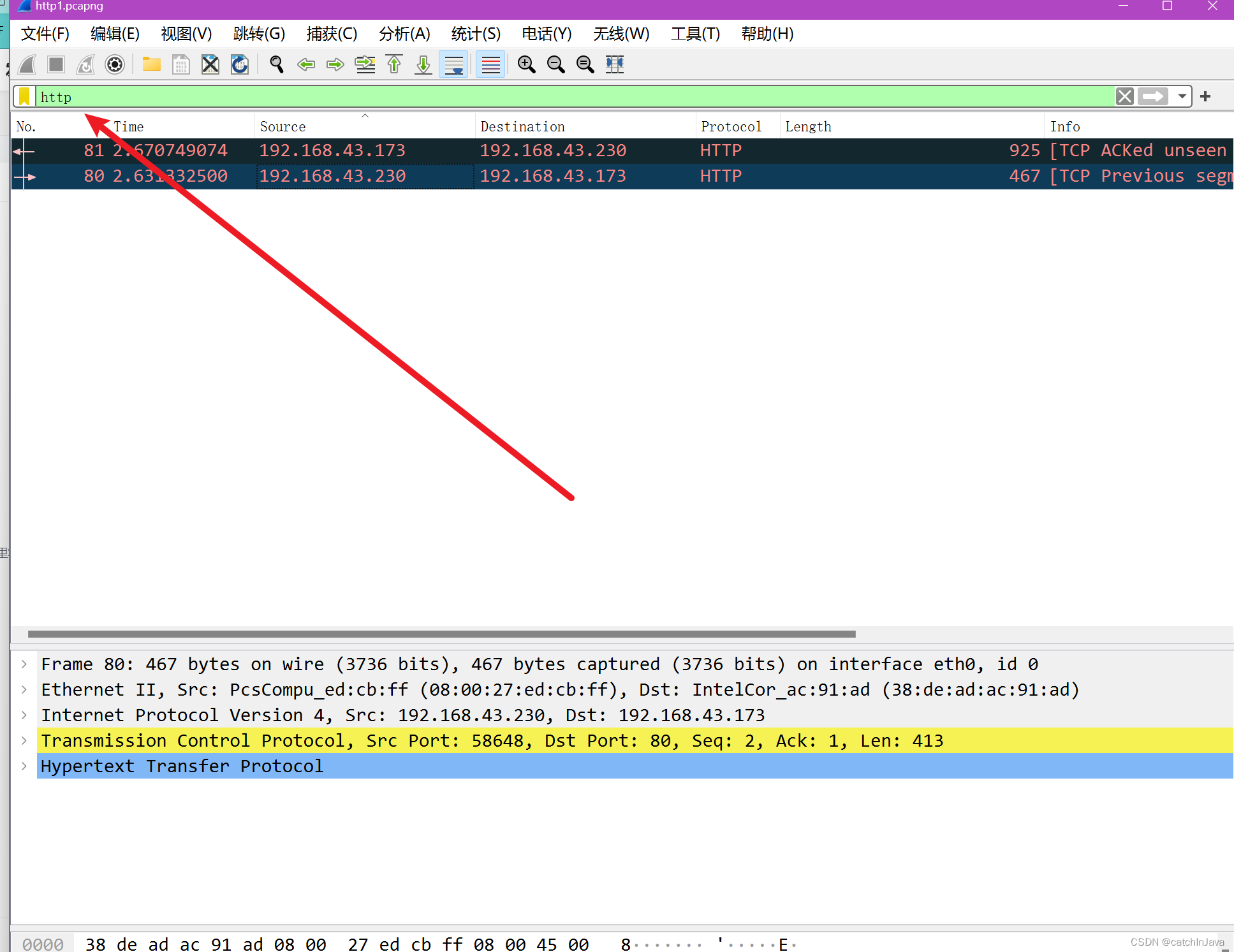
CTF流量题解http1.pcapng
使用Wireshark工具打开流量文件http1.pcapng,如下图所示。 在过滤检索栏输入http,wireshark自动进行过滤。...

若依vue前端有全局用户信息变量吗
"若依"是一个基于SpringBoot和Vue的前后端分离的开源项目。在前端Vue部分,全局用户信息通常保存在Vuex中,Vuex是Vue.js的状态管理模式。它提供了一个集中式存储来管理所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生…...
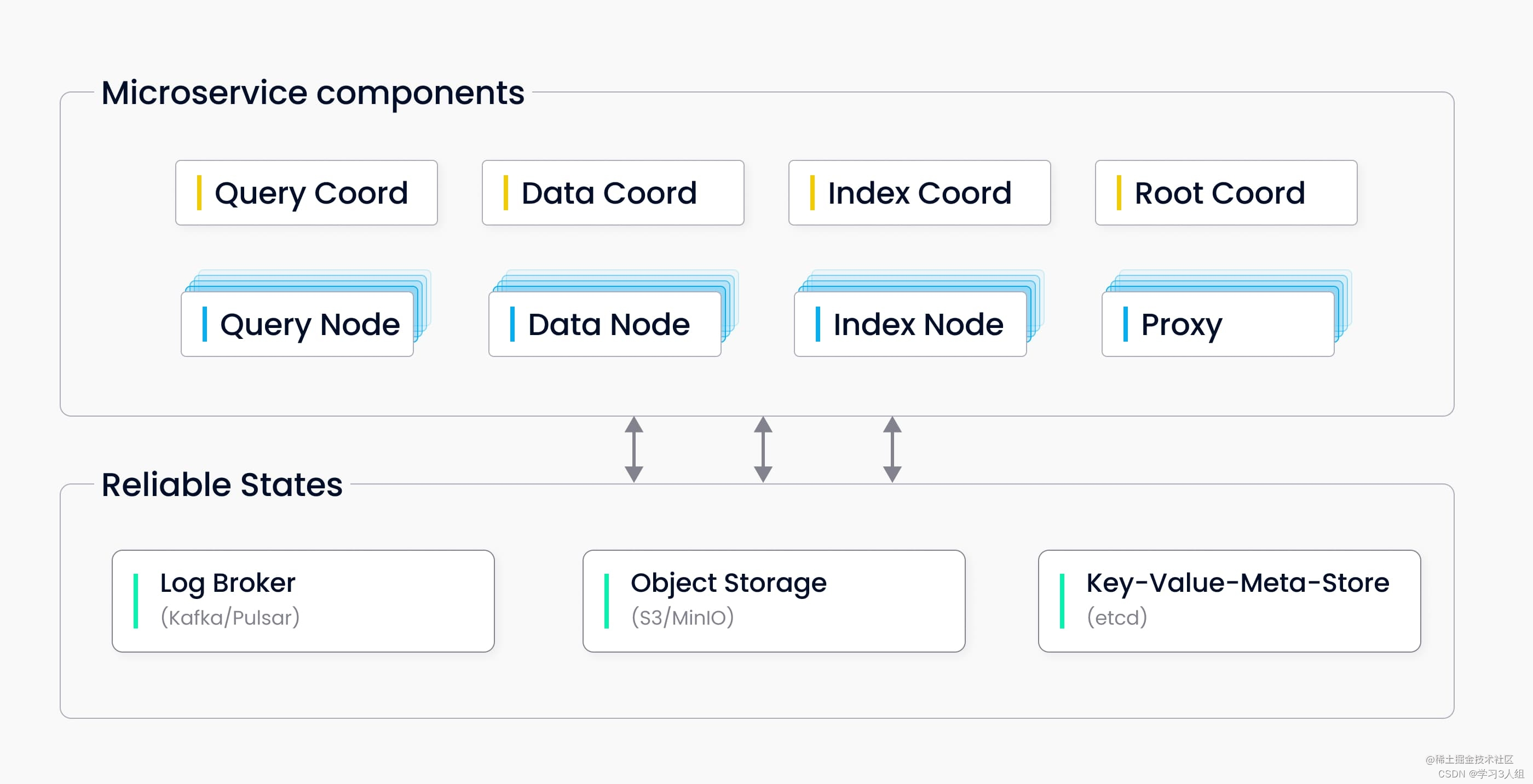
什么是Milvus
原文出处:https://www.yii666.com/blog/393941.html 什么是Milvus Milvus 是一款云原生向量数据库,它具备高可用、高性能、易拓展的特点,用于海量向量数据的实时召回。 Milvus 基于 FAISS、Annoy、HNSW 等向量搜索库构建,核心是…...

如何快速实现三菱FX3U程序的无线下载?
1.系统概述 三菱PLC FX3u可以使用专用下载线通过计算机串口下载程序,同样也可以使用自制下载线缆,连接无线模块 DTD435M进行远程无线下载程序,计算机端采用RS232或者RS485 将计算机端与无线模块连接,PLC端同样使用RS232转RS485将…...

Flink源码之RPC
Flink是一个典型的Master/Slave分布式实时处理系统,分布式系统组件之间必然涉及通信,也即RPC,以下图展示Flink组件之间的关系: RPCGateWay 一般RPC框架可根据用户业务类生成客户端和服务器端通信底层代码,此时只需定…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
