Mindspore安装
本文用于记录搭建昇思MindSpore开发及使用环境的过程,并通过MindSpore的API快速实现了一个简单的深度学习模型。
什么是MindSpore?
昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景覆盖三大目标。
安装步骤
鉴于笔者手头硬件资源有限,这里采用的环境是CPU。如下是在CPU环境的Windows系统上,使用pip方式快速安装MindSpore的步骤:
- 确认系统环境信息
- 确认安装Windows 10是x86架构64位操作系统。
- 确认安装Python(>=3.7.5),已有Python环境是Python3.9.7版本,满足要求。
- 安装MindSpore
运行以下命令:
# Python3.9
pip install https://ms-release.obs.cn-north-4.myhuaweicloud.com/2.0.0a0/MindSpore/cpu/x86_64/mindspore-2.0.0a0-cp39-cp39-win_amd64.whl --trusted-host ms-release.obs.cn-north-4.myhuaweicloud.com -i https://pypi.tuna.tsinghua.edu.cn/simple
在联网状态下,安装whl包时会自动下载mindspore安装包的依赖项。
安装报错 :
ERROR: Could not install packages due to an OSError: [WinError 5] 拒绝访问。: 'D:\\Program Files\\Anaconda\\Lib\\site-packages\\~-mpy\\.libs\\libopenblas.FB5AE2TYXYH2IJRDKGDGQ3XBKLKTF43H.gfortran-win_amd64.dll' Consider using the `--user` option or check the permissions.

这是因为pip安装模块的权限不够导致失败,笔者是通过执行下面的命令得以解决。
pip install -i http://pypi.douban.com/simple/ pip -U --trusted-host pypi.douban.com --user
执行完上述命令之后再次安装mindspore,如下图。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sRliKJ4o-1676715767200)(imgs/230217155424.png)]

- 验证安装是否成功
python -c "import mindspore;mindspore.run_check()"
输出如下内容,表明安装成功。

快速入门
这里以手写体数字识别为例,体验了基于MindSpore的API实现深度学习模型的过程。
场景描述
本文使用Mindspore,基于Resnet50神经网络完成手写体数字识别。
数据集处理
下载Mnist数据集
Mnist数据集是机器学习领域的一款经典数据集,其中包括6w个训练样本和1w个测试样本,每个样本都是28*28像素的灰度手写数字图片,数字0-9共10类。通过如下代码下载:
# Download data from open datasets
from download import downloadurl = "https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/" \"notebook/datasets/MNIST_Data.zip"
path = download(url, "./", kind="zip", replace=True)
获取数据集对象
train_dataset = MnistDataset('MNIST_Data/train')
test_dataset = MnistDataset('MNIST_Data/test')
print(train_dataset.get_col_names()) #['image', 'label']
数据集目录如下,其中标记为images的是图片,labels是标签。

数据处理
数据集自动下载完成后,可使用数据处理模块 mindspore.dataset 进行预处理。这里采用的是流水线处理,在海量数据下,该处理模式可以实现数据的高效处理,当然也会占用更多的CPU和内存资源。
- 使用map对图像数据及标签进行变换处理,并将处理完的数据集打包,batchsize为64。map函数会将数据集中第二个参数的指定的列作为输入,调用第一个参数的处理函数执行处理,如果有多个处理函数,上一个函数的输出作为下一个函数的输入。其中,map的第一个参数是处理函数列表,第二个参数表示需要处理的列。
def data_process(dataset, batch_size):image_transforms = [#图像缩放,输出像素值output = image * rescale + shift.vision.Rescale(1.0 / 255.0, 0),#根据平均值和标准偏差对输入图像进行归一化,其中,mean是图像各个通道的均值,std是各个通道的标准差vision.Normalize(mean=(0.1307,), std=(0.3081,)),#转换图像格式,在不同的硬件设备中可能会对(height, width, channel)# 或(channel, height, width)两种不同格式有针对性优化。MindSpore设# 置HWC为默认图像格式,在有CWH格式需求时,可使用该变换进行处理。vision.HWC2CHW()]# 转为mindspore的int32格式label_transform = transforms.TypeCast(mindspore.int32)# 对各个图像按照流水线处理dataset = dataset.map(image_transforms, 'image')# 将各个标签转为int32类型dataset = dataset.map(label_transform, 'label')dataset = dataset.batch(batch_size)return datasettrain_dataset = data_process(train_dataset, 64)
test_dataset = data_process(test_dataset, 64)
- 使用create_tuple_iterator或create_dict_iterator对数据集进行迭代。
# image, label = next(train_dataset.create_tuple_iterator())for image, label in test_dataset.create_tuple_iterator():print(f"Shape of image [N, C, H, W]: {image.shape} {image.dtype}")print(f"Shape of label: {label.shape} {label.dtype}")breakfor data in test_dataset.create_dict_iterator():print(f"Shape of image [N, C, H, W]: {data['image'].shape} {data['image'].dtype}")print(f"Shape of label: {data['label'].shape} {data['label'].dtype}")break
网络构建
基于mindspore的nn.Cell类,构建Resnet50神经网络。
神经网络模型由神经网络层和Tensor操作构成,基于 mindspore.nn 可实现常见的神经网络层,其中 nn.Cell 类是构建所有网络的基类,也是网络的基本单元。一个神经网络模型可表示为一个Cell,它又是由
不同的子Cell组成。基于这样的嵌套结构,即可简单地使用面向对象编程的思维,对神经网络结构进行构建和管理。
定义模型类
定义神经网络模型继承nn.Cell类,再在__init__方法中进行子Cell的实例化和状态管理,在construct方法中实现Tensor操作。
class Network(nn.Cell):def __init__(self):super().__init__()self.flatten = nn.Flatten()self.dense_relu_sequential = nn.SequentialCell(nn.Dense(28*28, 512),nn.ReLU(),nn.Dense(512, 512),nn.ReLU(),nn.Dense(512, 10))def construct(self, x):x = self.flatten(x)logits = self.dense_relu_sequential(x)return logits
构建完成后,实例化Network对象,并查看结构。
model = Network()
print(model)

模型层分解
构造一个shape为(3, 28, 28)的随机数据(3个28x28的图像)。
input_image = ops.ones((3, 28, 28), mindspore.float32)
print(input_image.shape) #(3, 28, 28)
-
nn.Flatten
实例化nn.Flatten层,将28x28的2D张量转换为784大小的连续数组。
flatten = nn.Flatten() flat_image = flatten(input_image) print(flat_image.shape) # (3, 784) -
nn.Dense
nn.Dense为全连接层,其使用权重和偏差对输入进行线性变换。
layer1 = nn.Dense(in_channels=28*28, out_channels=20) hidden1 = layer1(flat_image) print(hidden1.shape) #(3, 20) -
nn.ReLU
nn.ReLU层给网络中加入非线性的激活函数,帮助神经网络学习各种复杂的特征。
print(f"Before ReLU: {hidden1}\n\n") hidden1 = nn.ReLU()(hidden1) print(f"After ReLU: {hidden1}")

-
nn.SequentialCell
nn.SequentialCell是一个有序的Cell容器。输入Tensor将按照定义的顺序通过所有Cell。我们可以使用SequentialCell来快速组合构造一个神经网络模型。
seq_modules = nn.SequentialCell(flatten,layer1,nn.ReLU(),nn.Dense(20, 10) )logits = seq_modules(input_image) print(logits.shape) #(3,10) -
nn.Softmax
最后使用nn.Softmax将神经网络最后一个全连接层返回的logits的值缩放为[0, 1],表示每个类别的预测概率。axis指定的维度数值和为1。
softmax = nn.Softmax(axis=1) pred_probab = softmax(logits)输出如下:
[[0.09906127 0.09989168 0.101061 0.10052359 0.09982764 0.1007046 0.10100672 0.09960879 0.09997301 0.09834171] [0.09906127 0.09989168 0.101061 0.10052359 0.09982764 0.1007046 0.10100672 0.09960879 0.09997301 0.09834171] [0.09906127 0.09989168 0.101061 0.10052359 0.09982764 0.1007046 0.10100672 0.09960879 0.09997301 0.09834171]]
模型参数
网络内部神经网络层具有权重参数和偏置参数(如nn.Dense),这些参数会在训练过程中不断进行优化,可通过 model.parameters_and_names() 来获取参数名及对应的参数详情。
print(f"Model structure: {model}\n\n")for name, param in model.parameters_and_names():print(f"Layer: {name}\nSize: {param.shape}\nValues : {param[:2]} \n")

模型训练
#定义损失函数和优化器
loss_fn = nn.CrossEntropyLoss()
optimizer = nn.SGD(model.trainable_params(), 1e-2)
通常,一个完成的模型训练过程包括如下三步:
- 正向计算:模型对结果预测,输出logits值,并与正确标签label求预测损失loss。
- 反向传播:利用自动微分机制,自动求模型参数(parameters)对于loss的梯度(gradients)。
- 参数优化:将梯度更新到参数上。
# 定义正向计算函数
def forward_fn(data, label):logits = model(data)loss = loss_fn(logits, label)return loss, logits#通过mindspore中的函数变换获取梯度计算函数
grad_fn = mindspore.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=True)# 定义训练函数
def train_step(data, label):(loss, _), grads = grad_fn(data, label)optimizer(grads)return lossdef train(model, dataset):size = dataset.get_dataset_size()model.set_train()for batch, (data, label) in enumerate(dataset.create_tuple_iterator()):loss = train_step(data, label)if batch % 100 == 0:loss, current = loss.asnumpy(), batchprint(f"loss: {loss:>7f} [{current:>3d}/{size:>3d}]")
定义测试函数,评估模型性能。
def test(model, dataset, loss_fn):num_batches = dataset.get_dataset_size()model.set_train(False)total, test_loss, correct = 0, 0, 0for data, label in dataset.create_tuple_iterator():pred = model(data)total += len(data)test_loss += loss_fn(pred, label).asnumpy()correct += (pred.argmax(1) == label).asnumpy().sum()test_loss /= num_batchescorrect /= totalprint(f"Test: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
训练过程需多次迭代数据集,一次完整的迭代称为一轮(epoch)。在每一轮,遍历训练集进行训练,结束后使用测试集进行预测。打印每一轮的loss值和预测准确率(Accuracy),可以看出,
loss不断下降,准确度不断提高。
epochs = 3
for t in range(epochs):print(f"Epoch {t+1}\n-------------------------------")train(model, train_dataset)test(model, test_dataset, loss_fn)
print("Done!")

保存模型
模型训练完成后,将参数进行保存。
# Save checkpoint
mindspore.save_checkpoint(model, "model.ckpt")
print("Saved Model to model.ckpt")
加载模型
加载模型包括两步,具体如下。
# 实例化模型对象,构造模型。
model = Network()
# 加载模型参数,并将其加载至模型上。
param_dict = mindspore.load_checkpoint("model.ckpt")
param_not_load = mindspore.load_param_into_net(model, param_dict)
#param_not_load是未被加载的参数列表,为空时代表所有参数均加载成功。
print(param_not_load)#[]
模型推理
加载后的模型即可直接用于预测推理。
model.set_train(False)
for data, label in test_dataset:pred = model(data)predicted = pred.argmax(1)print(f'Predicted: "{predicted[:10]}", Actual: "{label[:10]}"')break

相关文章:

Mindspore安装
本文用于记录搭建昇思MindSpore开发及使用环境的过程,并通过MindSpore的API快速实现了一个简单的深度学习模型。 什么是MindSpore? 昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景覆盖三大目标。 安装步骤 鉴于笔者手头硬…...

C++010-C++嵌套循环
文章目录C010-C嵌套循环嵌套循环嵌套循环举例题目描述 输出1的个数题目描述 输出n行99乘法表题目描述 求s1!2!...10!作业在线练习:总结C010-C嵌套循环 在线练习: http://noi.openjudge.cn/ https://www.luogu.com.cn/ 嵌套循环 循环可以指挥计算机重复去…...
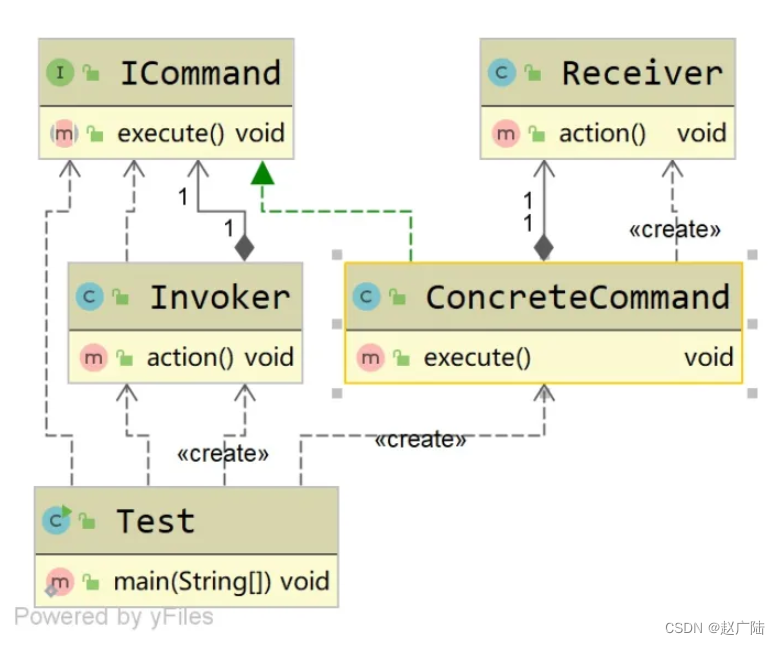
设计模式之迭代器模式与命令模式详解和应用
目录1 迭代器模式1.1 目标1.2 内容定位1.3 迭代器模式1.4 迭代器模式的应用场景1.5 手写字定义的送代器1.6 迭代器模式在源码中的体现1.7 迭代器模式的优缺点2 命令模式2.1 定义2.2 命令模式的应用场景2.3 命令模式在业务场景中的应用2.4 命令模式在源码中的体现2.5 命令模式的…...

【QA】[Vue/复选框全选] v-model绑定每一项的赋初值问题
发生场景:不只是复选框的状态改变,还有的功能要用到复选框的选中状态,比如:购物车计算总价,合计等等。 引入:复选框 checkbox 在使用时,需要用v-model绑定布尔值,来获取选中状态&…...
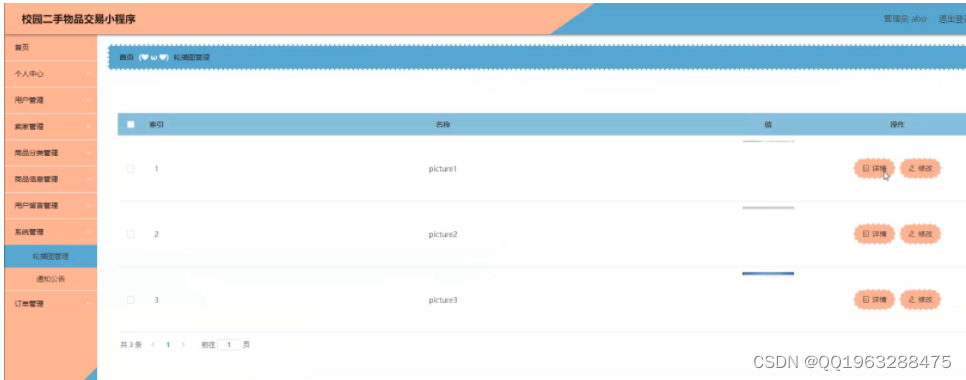
python基于django+vue微信小程序的校园二手闲置物品交易
在大学校园里,存在着很多的二手商品,但是由于信息资源的不流通以及传统二手商品信息交流方式的笨拙,导致了很多仍然具有一定价值或者具有非常价值的二手商品的囤积,乃至被当作废弃物处理。现在通过微信小程序的校园二手交易平台,可以方便快捷的发布和交流任何二手商品的信息,并…...

设计模式之观察者模式
什么是观察者模式 观察者模式定义了对象之间一种一对多依赖关系,使得每当一个对象状态发生改变时,其相关依赖对象都能收到通知并自动刷新。 观察者模式主要包含以下几个角色: Subject(目标):指被观察的对…...

Java Lambda表达式
目录1 Lambda表达式1.1 函数式编程思想概括1.2 Lambda表达式标准格式1.3 Lambda表达式练习1(抽象方法无参无返回值)1.4 Lambda表达式练习2(抽象方法带参无返回值)1.5 Lambda表达式练习2(抽象方法带参带返回值ÿ…...

【1237. 找出给定方程的正整数解】
来源:力扣(LeetCode) 描述: 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子…...

java基础学习 day41(继承中成员变量和成员方法的访问特点,方法的重写)
继承中,成员变量的访问特点 a. name前什么都不加,name变量的访问采用就近原则,先在局部变量中查找,若没找到,继续在本类的成员变量中查找,若没找到,继续在直接父类的成员变量中查找,…...

【c语言进阶】深度剖析整形数据
🚀write in front🚀 📜所属专栏: 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对我最大的激励…...
)
【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人)
【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人) 这里写目录标题【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人)一.项目采购管理记忆敲出1.合同管理:2.规划采购管…...
[LeetCode 1237]找出给定方程的正整数解
题目描述 题目链接:[LeetCode 1237]找出给定方程的正整数解 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知…...
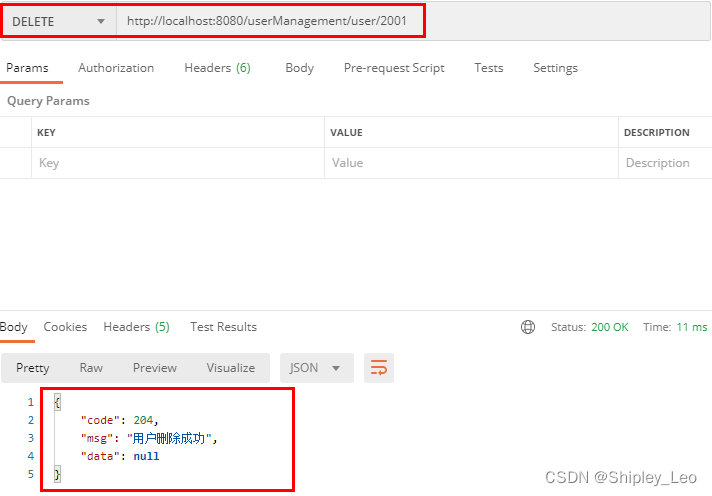
6.2 构建 RESTful 应用接口
第6章 构建 RESTful 服务 6.1 RESTful 简介 6.2 构建 RESTful 应用接口 6.3 使用 Swagger 生成 Web API 文档 6.4 实战:实现 Web API 版本控制 6.2 构建 RESTful 应用接口 6.2.1 Spring Boot 对 RESTful 的支持 Spring Boot 提供的spring-boot-starter-web组件完全…...

20230218英语学习
How Italian Artist’s Mild Colors Dominate World of Design 温柔的“莫兰迪色”,如何引领设计时尚? The Morandi color scheme has become an across-the-board fashion that now prevails in the world of design.Soft and sophisticated Morandi c…...

Linux单一服务管理systemctl
基本上systemd这个启动服务机制只有systemctl命令来处理,所以全部的操作都需要使用systemctl systemctl管理单一服务 一般来说服务的启动有两个阶段,一个是开机是否启动,以及现在是否启动 systemctl【command】【unit】 command主要有&…...
【GStreamer 】 TX1中CPU和GPU解码显示海康相机RTSP流
大家好,我是虎哥,今天找了一套海康的相机,想后续测试一下DeepStream用网络相机RTSP流做输入看看后续目标识别和分类。但是还是想先实时看看视频,当然,可以选择VLC去查看,顺道我也用GStreamer 来测试了一下&…...

匿名内部类、Lambda表达式、方法引用对比分析
文章目录一、匿名内部类1. 语法格式2. 使用方法① 传统方式② 匿名内部类方式二、Lambda表达式1. 语法格式2. 使用方法① 匿名内部类方式② Lambda表达式方式三、方法引用1. 语法格式2. 使用方法① 类型的静态方法引用② 类型的构造方法引用③ 类型的实例方法引用④ 对象的实例…...
ESXi主机CVE-2021-21972漏洞复现安全处置建议
一、漏洞简介 vSphere 是 VMware 推出的虚拟化平台套件,包含 ESXi、vCenter Server 等一系列的软件。其中 vCenter Server 为 ESXi 的控制中心,可从单一控制点统一管理数据中心的所有 vSphere 主机和虚拟机。 vSphere Client(HTML5…...

研报精选230217
目录 【行业230217毕马威】奢侈品行业新气象【行业230217国信证券】医药生物行业2023年2月投资策略:持续关注疫后复苏和创新两大主线【行业230217国金证券】航空锻造:稳定格局筑专业化壁垒,顺势而为拓产业链深度【个股230217西南证券_招商轮船…...
(std::unordered_set)(一))
c++11 标准模板(STL)(std::unordered_set)(一)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
