Pytorch 基础之张量数据类型
学习之前:先了解 Tensor(张量)
官方文档的解释是:
张量如同数组和矩阵一样, 是一种特殊的数据结构。在PyTorch中, 神经网络的输入、输出以及网络的参数等数据, 都是使用张量来进行描述。
说白了就是一种数据结构
基本数据类型
Java 与 Pytorch 基本数据类型类比:
| Java | Pytorch (所有都是 Tensor) |
|---|---|
| byte | ByteTensor of size() |
| short | ShortTensor of size() |
| char | Charensor of size() |
| int | IntTensor of size() |
| long | LongTensor of size() |
| float | FloatTensor of size() |
| double | DoubleTensor of size() |
Pytorch 并没有 string 这种类型,但可以通过 one-hot 编码,以及一些内置的处理库,如 Word2vec 来表示。这块先有个概念,了解即可。
数组的表示形如:IntTensor of size[d1, d2, ...],FloatTensor of size[d1, d2, ...] ...
Pytorch 具体的类型如下图:

Pytorch 数据类型在 CPU 和 GPU 运行上有些差别,在 GPU 注意加上 cuda
类型检查
Pytorch 提供了以下几种类型检查与判断的方法,举例来说:
import torch
x=torch.rand(5,3) // 随机生成一个 5 行 4 列的 tensor 变量
print(x.type())
print(type(x))
result = isinstance(x, torch.FloatTensor)
print(result)// 执行结果
torch.FloatTensor
<class 'torch.Tensor'>
True执行结果如下:
| 方法 | 结果 |
|---|---|
| x.type() | torch.FloatTensor,返回当前这个变量具体的数据类型 |
| type(x) | <class 'torch.Tensor'>,返回当前这个变量的类型 |
| isinstance(x, torch.FloatTensor) | True,数据类型比较,这里改成 FloatTensor 的父类 torch.Tensor 也是返回 True |
如下图:Tensor 的实现类有以下好几种。
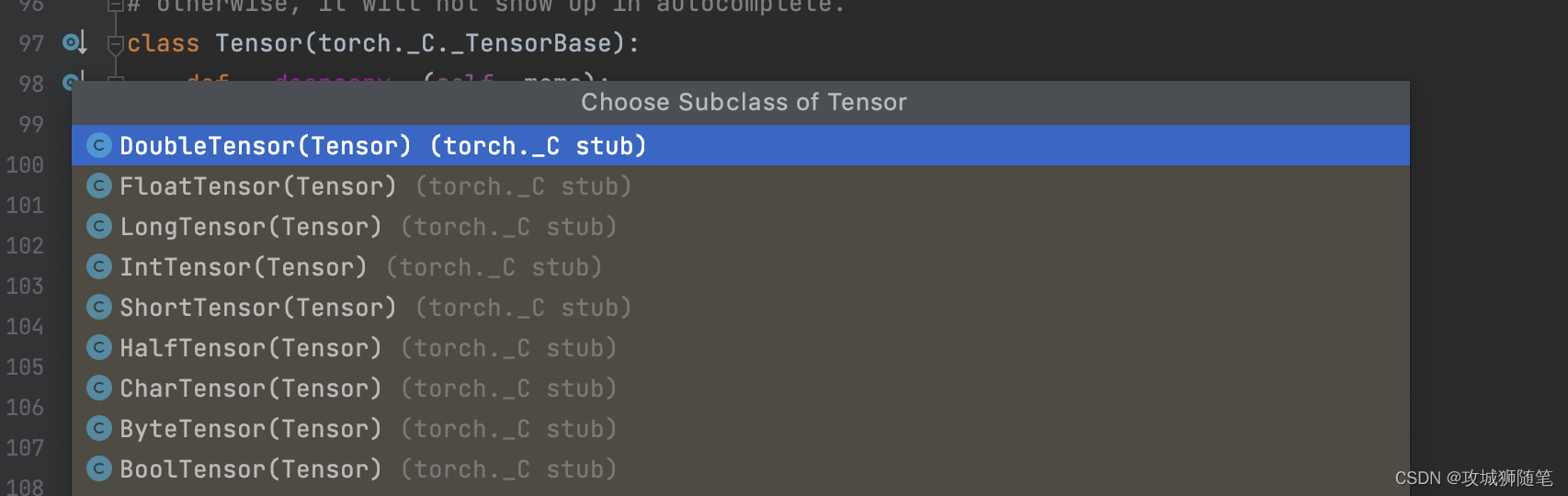
维度(dimension)
Tensor 的维度,可通过以下方法来计算:
# 创建个具体数据的 Tensor dim = 0
a = torch.tensor(1)
print(a.shape)
print(a.size())
print(a.dim())
print(len(a.shape))
print(len(a.size()))//输出结果:
torch.Size([])
torch.Size([])
0
0
0shape 属性:是描述 Tensor 的形状
size() 方法:和 shape 属性一样,只是这是方法
dim() 方法:直接获取维度的数值,也可通过 len(a.shape) 和 len(a.size()) 方法来获取
维度的理解一定是要结合实际的意义来,这样会更容易理解。
零维度 Tensor
如上代码,就是零维度,实际使用场景:loss 损失函数,返回的就是个 0 维标量,表示数据大小
Pytorch 中需要表示数据大小的,都是使用零维度
1 维度 Tensor
b = torch.tensor([5, 4])
print(b)
print(b.shape)
print(b.size())
print(b.dim())//输出结果
tensor([5, 4])
torch.Size([2])
torch.Size([2])
1可以理解为是一个 1 行 2 列的矩阵。
b.size() 返回的 torch.Size([2]),表示的就是只有 1 行 2 列的结构
实际使用的场景是:Bias(偏置函数)、线性输入
2 维度 Tensor
c = torch.rand(2, 3)
print(c)
print(c.size())
print(c.size(0))
print(c.size(1))
print(c.dim())//输出结果
tensor([[0.5755, 0.1844, 0.1174],[0.8228, 0.8758, 0.1008]])
torch.Size([2, 3])
2
3
2可以理解为一个 2 行 3 列的矩阵。
c.size() 返回的 torch.Size([2, 3]) 描述的是矩阵结构,行数为 2,列数为 3
c.size(0):返回的是行数 2
c.size(1):返回的是列数 3
实际使用场景:线性输入组的概念,比如用 dimension 为 1 的 Tensor 表示一张图片,要输入 8 张,则就需要再增加一个维度。
3 维度 Tensor
d = torch.rand(2, 3, 4)
print(d)
print(d.size())
print(d.size(0))
print(d.size(1))
print(d.size(2))
print(d.dim())//输出结果
tensor([[[0.9375, 0.6131, 0.5574, 0.2307],[0.4352, 0.2731, 0.5670, 0.2216],[0.0959, 0.8864, 0.7924, 0.0760]],[[0.9787, 0.2835, 0.2164, 0.3175],[0.8904, 0.8363, 0.0011, 0.3942],[0.6285, 0.5877, 0.5401, 0.2004]]])
torch.Size([2, 3, 4])
2
3
4
3
可以理解为 2 组 3 行 4 列的矩阵构成的数据。
d.size(0):返回的是组数 2
d.size(1):返回的是行数 3
d.size(2):返回的是列数 4
实际使用场景: 比如用一个 dimension 长度为 1 的 Tensor 表示图片的高度,用另一个 dimension 长度为 1 的 Tensor 表示图片的宽度,如果要输入 10 张图片则需要再增加一个维度,也就是 3 维的 Tensor 表示这个输入。在 RNN (循环神经网络) 处理中有更广泛应用。
4 维度 Tensor
e = torch.rand(2, 3, 28, 28)
print(e)
print(e.size())
print(e.size(0))
print(e.size(1))
print(e.size(2))
print(e.size(3))
print(e.dim())//输出结果
tensor([[[[0.7386, 0.8259, 0.6421, 0.5180, 0.7754],[0.2118, 0.0453, 0.4092, 0.2339, 0.7938],[0.2132, 0.0554, 0.0305, 0.3132, 0.8126],[0.2169, 0.2510, 0.5233, 0.1525, 0.4049],[0.5695, 0.8084, 0.4958, 0.6022, 0.6873]],[[0.8591, 0.4062, 0.0522, 0.4481, 0.8709],[0.1667, 0.1246, 0.0640, 0.3585, 0.0226],[0.7756, 0.3169, 0.1678, 0.3884, 0.3878],[0.6382, 0.8963, 0.3272, 0.9765, 0.6208],[0.1300, 0.4894, 0.0875, 0.5357, 0.5581]],[[0.9978, 0.4991, 0.8405, 0.8512, 0.8052],[0.3975, 0.8562, 0.1375, 0.0642, 0.0928],[0.2272, 0.7209, 0.8362, 0.3370, 0.7584],[0.9186, 0.0423, 0.5342, 0.6597, 0.8330],[0.2812, 0.3573, 0.2112, 0.7046, 0.8038]]],[[[0.0577, 0.9690, 0.1507, 0.8940, 0.4517],[0.8458, 0.2516, 0.3659, 0.3188, 0.6680],[0.0421, 0.0674, 0.8306, 0.2685, 0.3755],[0.5505, 0.9351, 0.5172, 0.6399, 0.0379],[0.3950, 0.6902, 0.6320, 0.6701, 0.1980]],[[0.7649, 0.6655, 0.4616, 0.4521, 0.9183],[0.4430, 0.8904, 0.7241, 0.6998, 0.3434],[0.8955, 0.8490, 0.1604, 0.6503, 0.5091],[0.5581, 0.9493, 0.6065, 0.7257, 0.1195],[0.2835, 0.5829, 0.5373, 0.2529, 0.6760]],[[0.8280, 0.6496, 0.8250, 0.9196, 0.3306],[0.0847, 0.9219, 0.3239, 0.7554, 0.3148],[0.2311, 0.5712, 0.5821, 0.8725, 0.7012],[0.9260, 0.8914, 0.4068, 0.7549, 0.6963],[0.7220, 0.2854, 0.0995, 0.9733, 0.9665]]]])
torch.Size([2, 3, 5, 5])
2
3
5
5
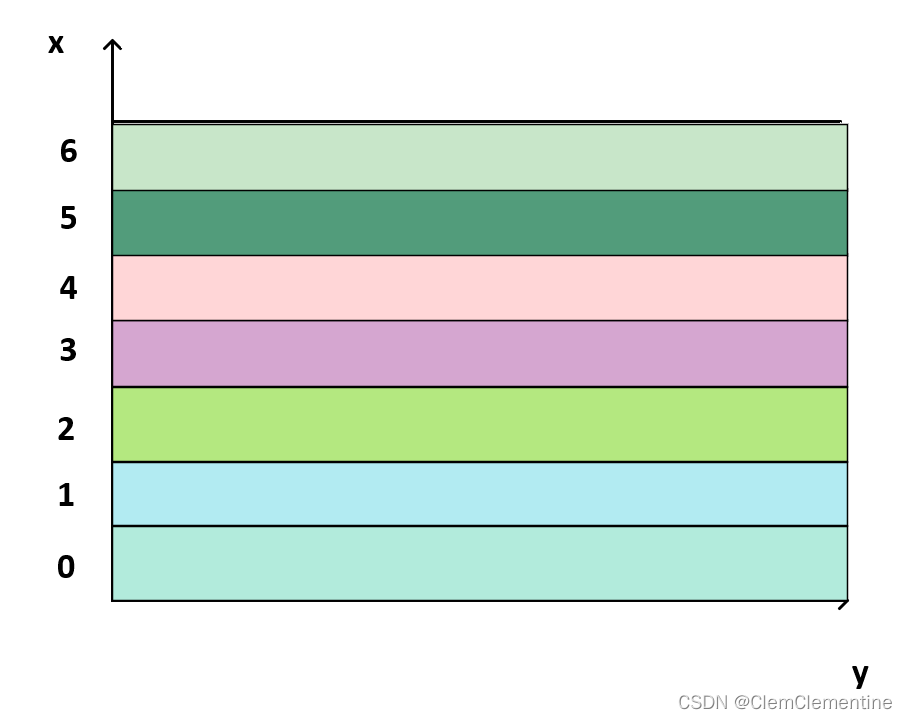
4可以理解为 2 组 3 块 5 行 5 列的矩阵构成的数据。
e.size(0):返回的是组数 2
e.size(1):返回的是块数 3
e.size(2):返回的是行数 5
e.size(3):返回的是列数 5
实际应用场景:图片的处理,比如要输入 2 张由 3 个颜色通道组成的,高为 5 个像素,宽为 5 个像素。在 CNN(卷积神经网络)中应用更为广泛。
以上是对 Pytorch 的 Tensor 张量数据类型进行了一些简单的介绍,有不足之处,欢迎一起探讨。
相关文章:

Pytorch 基础之张量数据类型
学习之前:先了解 Tensor(张量) 官方文档的解释是: 张量如同数组和矩阵一样, 是一种特殊的数据结构。在PyTorch中, 神经网络的输入、输出以及网络的参数等数据, 都是使用张量来进行描述。 说白了就是一种数据结构 基本数据类型…...
Java 基础面试题——常见类
目录1.String 为什么是不可变的?2.字符串拼接用“” 和 StringBuilder 有什么区别?3.String、StringBuffer 和 StringBuilder 的区别是什么?4.String 中的 equals() 和 Object 中的 equals() 有何区别?5.Object 类有哪些常用的方法?6.如何获…...

Windows 系统从零配置 Python 环境,安装CUDA、CUDNN、PyTorch 详细教程
文章目录1 配置 python 环境1.1 安装 Anaconda1.2 检查环境安装成功1.3 创建虚拟环境1.4 进入/退出 刚刚创建的环境1.5 其它操作1.5.1 查看电脑上所有已创建的环境1.5.2 删除已创建的环境2 安装 CUDA 和 CUDNN2.1 查看自己电脑支持的 CUDA 版本2.2 安装 CUDA2.3 安装 CUDNN2.4 …...
[REDIS]redis的一些配置文件
修改配置文件 vim /etc/redis/redis.conf目录 protected-mode tcp-backlog timeout tcp-keepalive daemonize pidfile loglevel databases 设置密码 maxclients maxmemory maxmemory-policy maxmemory-samples 默认情况下 bind127.0.0.1 只能接受本机的访问请求。在不写的情况…...

Java反序列化漏洞——CommonsCollections4.0版本—CC2、CC4
一、概述4.0版本的CommonsCollections对之前的版本做了一定的更改,那么之前的CC链反序列化再4版本中是否可用呢。实际上是可用的,比如CC6的链,引入的时候因为⽼的Gadget中依赖的包名都是org.apache.commons.collections ,⽽新的包…...

下载网上压缩包(包含多行json)并将其转换为字典的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...

【郭东白架构课 模块一:生存法则】11|法则五:架构师为什么要关注技术体系的外部适应性?
你好, 我是郭东白。 前四条法则分别讲了目标、资源、人性和技术周期,这些都与架构活动的外部环境有关。那么今天我们来讲讲在架构活动内部,也就是在架构师可控的范围内,应该遵守哪些法则。今天这节课,我们就先从技术体…...

Mindspore安装
本文用于记录搭建昇思MindSpore开发及使用环境的过程,并通过MindSpore的API快速实现了一个简单的深度学习模型。 什么是MindSpore? 昇思MindSpore是一个全场景深度学习框架,旨在实现易开发、高效执行、全场景覆盖三大目标。 安装步骤 鉴于笔者手头硬…...

C++010-C++嵌套循环
文章目录C010-C嵌套循环嵌套循环嵌套循环举例题目描述 输出1的个数题目描述 输出n行99乘法表题目描述 求s1!2!...10!作业在线练习:总结C010-C嵌套循环 在线练习: http://noi.openjudge.cn/ https://www.luogu.com.cn/ 嵌套循环 循环可以指挥计算机重复去…...
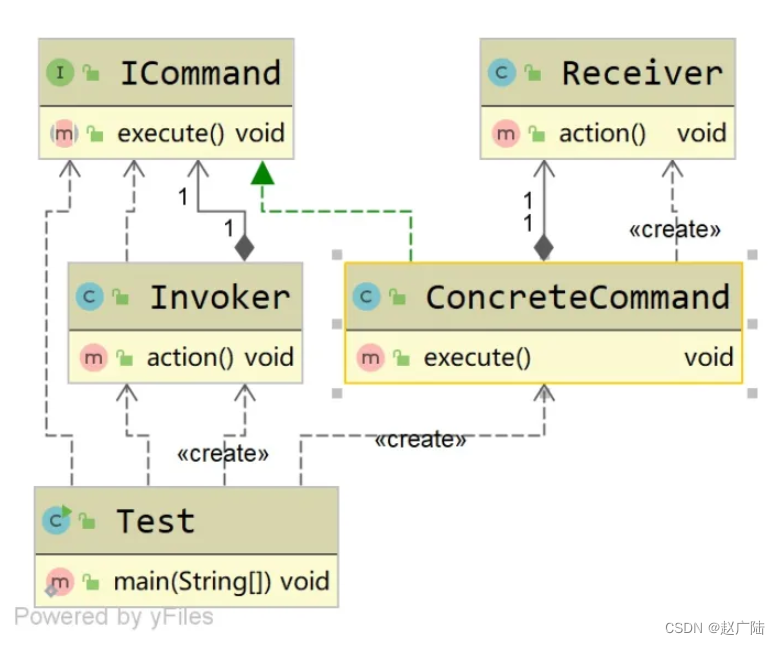
设计模式之迭代器模式与命令模式详解和应用
目录1 迭代器模式1.1 目标1.2 内容定位1.3 迭代器模式1.4 迭代器模式的应用场景1.5 手写字定义的送代器1.6 迭代器模式在源码中的体现1.7 迭代器模式的优缺点2 命令模式2.1 定义2.2 命令模式的应用场景2.3 命令模式在业务场景中的应用2.4 命令模式在源码中的体现2.5 命令模式的…...

【QA】[Vue/复选框全选] v-model绑定每一项的赋初值问题
发生场景:不只是复选框的状态改变,还有的功能要用到复选框的选中状态,比如:购物车计算总价,合计等等。 引入:复选框 checkbox 在使用时,需要用v-model绑定布尔值,来获取选中状态&…...
python基于django+vue微信小程序的校园二手闲置物品交易
在大学校园里,存在着很多的二手商品,但是由于信息资源的不流通以及传统二手商品信息交流方式的笨拙,导致了很多仍然具有一定价值或者具有非常价值的二手商品的囤积,乃至被当作废弃物处理。现在通过微信小程序的校园二手交易平台,可以方便快捷的发布和交流任何二手商品的信息,并…...

设计模式之观察者模式
什么是观察者模式 观察者模式定义了对象之间一种一对多依赖关系,使得每当一个对象状态发生改变时,其相关依赖对象都能收到通知并自动刷新。 观察者模式主要包含以下几个角色: Subject(目标):指被观察的对…...

Java Lambda表达式
目录1 Lambda表达式1.1 函数式编程思想概括1.2 Lambda表达式标准格式1.3 Lambda表达式练习1(抽象方法无参无返回值)1.4 Lambda表达式练习2(抽象方法带参无返回值)1.5 Lambda表达式练习2(抽象方法带参带返回值ÿ…...

【1237. 找出给定方程的正整数解】
来源:力扣(LeetCode) 描述: 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子…...

java基础学习 day41(继承中成员变量和成员方法的访问特点,方法的重写)
继承中,成员变量的访问特点 a. name前什么都不加,name变量的访问采用就近原则,先在局部变量中查找,若没找到,继续在本类的成员变量中查找,若没找到,继续在直接父类的成员变量中查找,…...

【c语言进阶】深度剖析整形数据
🚀write in front🚀 📜所属专栏: 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对我最大的激励…...
)
【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人)
【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人) 这里写目录标题【信息系统项目管理师】项目管理十大知识领域记忆敲出(采购风险沟通干系人)一.项目采购管理记忆敲出1.合同管理:2.规划采购管…...
[LeetCode 1237]找出给定方程的正整数解
题目描述 题目链接:[LeetCode 1237]找出给定方程的正整数解 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知…...
6.2 构建 RESTful 应用接口
第6章 构建 RESTful 服务 6.1 RESTful 简介 6.2 构建 RESTful 应用接口 6.3 使用 Swagger 生成 Web API 文档 6.4 实战:实现 Web API 版本控制 6.2 构建 RESTful 应用接口 6.2.1 Spring Boot 对 RESTful 的支持 Spring Boot 提供的spring-boot-starter-web组件完全…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
