匈牙利算法详解
匈牙利算法(Hungarian Algorithm)是一种组合优化算法(combinatorial optimization algorithm),用于求解指派问题(assignment problem),算法时间复杂度为O(N^3)。Harold Kuhn发表于1955年,由于该算法基于两位匈牙利数学家的早期研究成果,所以被称作“匈牙利算法”。
假设有三位工人A,B和C,需要分配他们每人完成一件工作;对于不同的工作他们所需要花费的时间不同,如下表所示。问题就是要找到一套耗时最小的指派方案。用矩阵表示如下:

匈牙利算法包含四步。前两步一次执行完,第三步和第三步会重复执行直到最优分配出现。算法的输入是n*n的矩阵,只有非负数。
Step 1: Subtract row minima (减去行最小值)
对于每一行,找到该行的最小值,然后该行的数都减去这个最小值
Step 2: Subtract column minima(减去列最小值)
同样的,对于每一列,找到该列的最小值,然后该列的数都减去这个最小值
Step 3: Cover all zeros with a minimum number of lines(用最少的线覆盖所有的0)
用最少的水平线和垂直线覆盖掉矩阵的所有0元素。如果需要n条线,那么在这些0中就存在最优解。算法结束
如果需要的线<n,继续第四步
Step 4: Create additional zeros(创建额外的0元素)
在第三步的的矩阵中,找到没被线覆盖的行列中的最小的元素,记作k。所有没被覆盖的元素都减去k,被覆盖两次的元素加上k。
第一步,找出每一行中值最小的元素,然后把该行所有元素都减去这一最小值:

第二步,对于每一列,找到该列的最小值,然后该列的数都减去这个最小值

第三步,用最少的水平线和垂直线覆盖掉矩阵的所有0元素。如果需要n条线,那么在这些0中就存在最优解。算法结束

可以看到当前的覆盖所有的0需要两条线,<n,继续第四步
第四步,找到没被线覆盖的行列中的最小的元素,记作k。所有没被覆盖的元素都减去k,被覆盖两次的元素加上k
 此时刚好用3条线即可覆盖所有的0,算法结束
此时刚好用3条线即可覆盖所有的0,算法结束

即最后指派A拖地,B擦桌,C扫厕所
二分图
1、一定不含有奇数环,可能包含长度为偶数的环, 不一定是连通图
2、二分图是图论中的一种特殊模型。设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交子集 ,使得每一条边都分别连接两个集合中的顶点。如果存在这样的划分,则此图为一个二分图,如下图所示的全都是二分图:

2.二分图的匹配
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
假设二分图的左边全为男生,右边全为女生,线连着的男女生为情侣关系,允许出现脚踏n条船等混乱的男女关系的情况,那么:
二分图的匹配:把二分图删除一些边使男女生之间的关系没有出现脚踏n条船的情况,就说删除边后得到的新图为一个匹配(允许出现单身狗的情况)
二分图的最大匹配:删除部分边使得保留的情侣数量最多,我们就称这个匹配为最大匹配。
比如在上面的4张图中,图1就是图3的一个最大匹配。
3、匈牙利算法的实现步骤
有如下图:

1.情况一(你是我的唯一)
首先我们看向男1,发现男1很纯情的只喜欢着女2,那么就成全他们吧。确定他们两个人的情侣关系。

2.情况二(你们都是我的翅膀)
接下来我们看向男2,发现男2喜欢着女1和女3两个女孩子。问问男2吧,他表示:我对这两个女孩子都是真心的,选谁都行!
选谁都行啊,那我们就随便选吧,把男2和女1牵上红线。

3.情况三(我会把你抢过来)
搞定,然后我们再看看男3,男3表示:我也喜欢女1啊!明明是我更加喜欢她!为什么?为什么她和别人在一起了啊!我不能接受!
嗯…看来我们的男3不想放弃啊,那我们尝试和男2交涉一下。
“男2呀,你有备胎吗?”
“有啊,怎么了?”
“男3看上了你女朋友,要不你和你备胎在一起,把你女朋友让给别人吧”
“嗯…好吧,记得让他请我吃饭”(作者对男2这种渣男表示强烈谴责!)
ok,这样的话事情就圆满解决了,可喜可贺可喜可贺。

4.情况四(我爱的人已经有了爱人)
解决了男2和男3的问题,我们再看向男4。
男4说:我喜欢女3!我想和女3在一起!
我看了看,女3不是男2的新女友吗?额…我再去找男2看看吧。
“什么?还要我换?大哥,我没别的备胎了,我拒绝!要是我还有备胎的话还差不多。”(作者对男2这种渣男表示强烈谴责!)
我们只好回头土脸的找到男4。那个,我们交涉失败了,女3是没戏了,要不你换一个追求对象我帮你争取一下?
男4低头沉思了一下,“我觉得吧,女4其实也挺可爱的。”
ok,安排!我们看了看,发现女4还是单身呢,那就成全你们吧。

最后,我们得到的最大匹配就是这样

总结:算法描述:
如果你想找的妹子已经有了男朋友,
你就去问问她男朋友,
你有没有备胎,
有备胎就把你女朋友让给我
你没有备胎我就只好找我的备胎
出处:1
2
代码:

#include <iostream>
#include <vector>using namespace std;// 使用DFS查找增广路径
bool dfs(vector<vector<int>>& graph, int u, vector<bool>& visited, vector<int>& match) {int m = graph.size();int n = graph[0].size();for (int v = 0; v < n; ++v) {if (graph[u][v] && !visited[v]) {visited[v] = true;// 如果v没有匹配或者可以找到增广路径if (match[v] == -1 || dfs(graph, match[v], visited, match)) {match[v] = u;return true;}}}return false;
}// 计算二分图的最大匹配数
int hungarian(vector<vector<int>>& graph) {int m = graph.size();int n = graph[0].size();vector<int> match(n, -1); // 存储匹配信息,match[i]表示右侧第i个节点的匹配节点编号int count = 0; // 最大匹配数for (int u = 0; u < m; ++u) {vector<bool> visited(n, false); // 记录每个节点的访问状态if (dfs(graph, u, visited, match)) {count++;}}return count;
}// 测试
int main() {vector<vector<int>> graph = {{1, 0, 1, 0},{1, 0, 0, 0},{0, 1, 1, 1},{0, 0, 1, 0}};int maxMatching = hungarian(graph);cout << "Maximum matching: " << maxMatching << endl;return 0;
}相关文章:

匈牙利算法详解
匈牙利算法(Hungarian Algorithm)是一种组合优化算法(combinatorial optimization algorithm),用于求解指派问题(assignment problem),算法时间复杂度为O(N^3)。Harold Kuhn发表于1955年,由于该算法基于两位匈牙利数学家的早期研究成果&#…...

script的三种加载模式
默认加载:阻断dom树构建(html文档解析),下载资源,然后立即执行,完毕后再进行dom树构建defer 加载:下载照旧,但执行延后。即下载资源和dom构建同时进行,但等dom树构建完再执行async:下…...

mongo 中两张表联合查询
表1:user 表 表2:dept表 需要查询user表中roleCodes 包含shr 的数据 然后联合dept表 需要部门名称 db.user.aggregate([{$match: {roleCodes: "shr" // 匹配roleCodes包含"shr"的文档}},{$lookup: {from: "dept", // 关联的集合名称loc…...

【Linux】多路转接 -- epoll
文章目录 1. 认识epoll2. epoll相关系统调用接口3. epoll工作原理4. epoll服务器5. epoll的优点6. epoll的工作方式7. epoll的使用场景 1. 认识epoll epoll系统调用和select以及poll是一样的,都是可以让我们的程序同时监视多个文件描述符上的事件是否就绪。 epoll…...
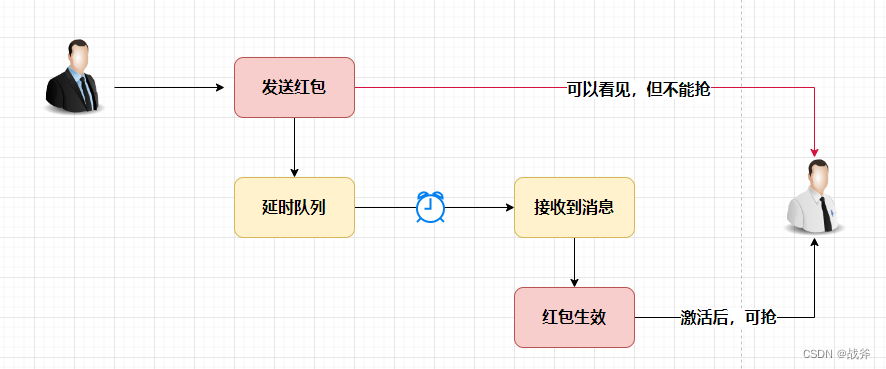
学会RabbitMQ的延迟队列,提高消息处理效率
系列文章目录 手把手教你,本地RabbitMQ服务搭建(windows) 消息队列选型——为什么选择RabbitMQ RabbitMQ灵活运用,怎么理解五种消息模型 RabbitMQ 能保证消息可靠性吗 推或拉? RabbitMQ 消费模式该如何选择 死信是什么…...
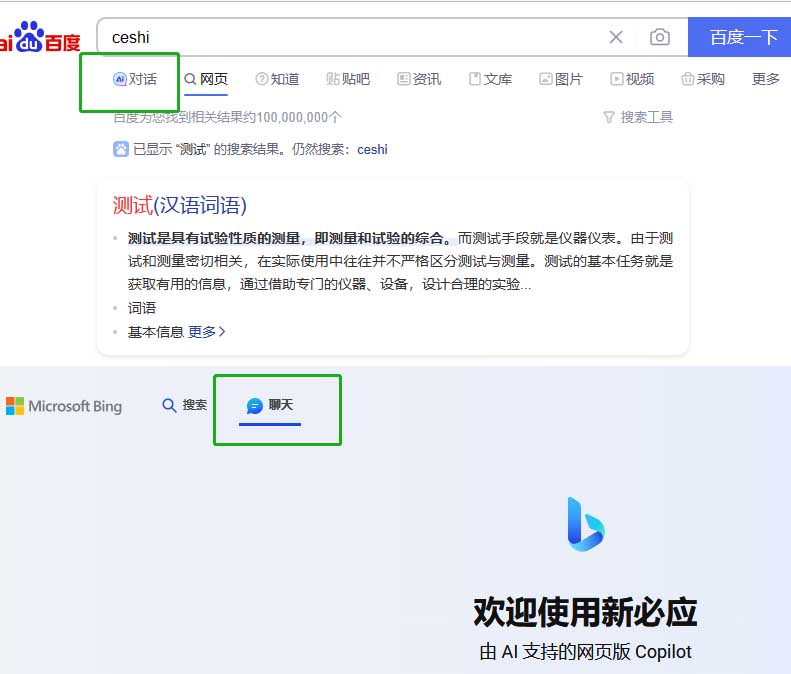
ChatGPT会取代搜索引擎吗?BingChat、GoogleBard与ChatGPT区别
目前暂时不会,ChatGPT为代表的聊天机器人很可能会直接集成到搜索中,而不是取代它。微软已经通过Bing Chat和Bing做到了这一点,它将“聊天”选项卡直接放入Bing搜索的菜单中。Google、百度也分别开始尝试通过其AI生成技术将Google Bard、文心一…...
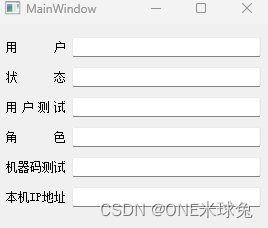
多个QLabel中文字左右对其问题研究
众所周知,关于QLabel 中的文字对其方式,官方提供多种,具体可参考 AlignmentFlag,这里就不详细列举了。 实际开发中有这样一个需求:多个lab中,文字显示不同,长度不一,但想要实现视觉…...
链式二叉树统计结点个数的方法和bug
方法一: 分治:分而治之 int BTreeSize1(BTNode* root) {if (root NULL) return 0;else return BTreeSize(root->left)BTreeSize(root->right)1; } 方法二: 遍历计数:设置一个计数器,对二叉树正常访问&#…...
: memory corruption: 0x0000000001496d90 ***)
C语言-报错集锦-03-malloc(): memory corruption: 0x0000000001496d90 ***
一、报错信息 [2023-8]--[ Debug ]--Push Data To StAccessPath OK. [2023-8]--[ Debug ]--Judge Vertex(0) Is Not Accessed. [2023-8]--[ Debug ]--Judge Vertex(2) Is Accessed. [2023-8]--[ Debug ]--Judge Vertex(3) Is Not Accessed. [2023-8]--[ Debug ]--Judge Vertex…...

现代C++中的从头开始深度学习:【5/8】卷积
一、说明 在上一个故事中,我们介绍了机器学习的一些最相关的编码方面,例如 functional 规划、矢量化和线性代数规划。 现在,让我们通过使用 2D 卷积实现实际编码深度学习模型来开始我们的道路。让我们开始吧。 二、关于本系列 我们将学习如何…...
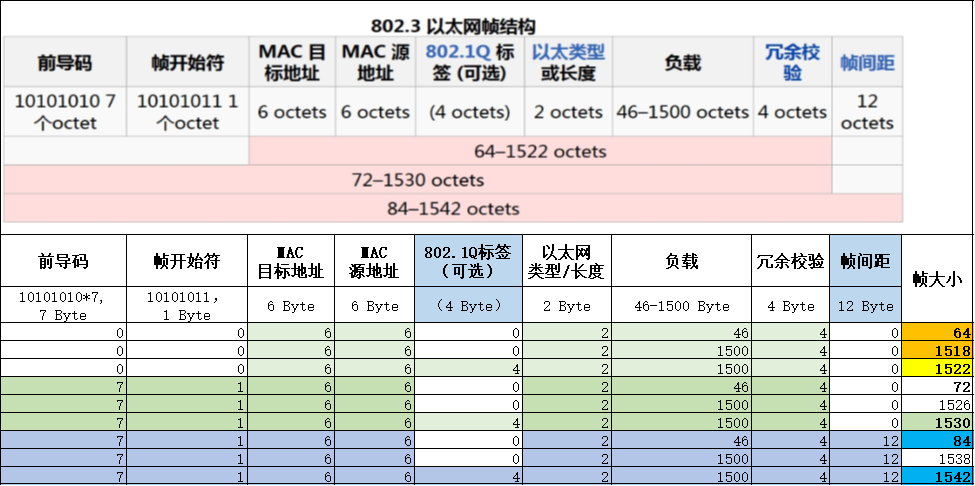
以太网帧格式与吞吐量计算
以太网帧结构 帧大小的定义 以太网单个最大帧 6(目的MAC地址) 6(源MAC地址) 2(帧类型) 1500{IP数据包[IP头(20)DATA(1480)]} 4(CRC校验ÿ…...

vue中install方法
1:语法 vue提供install可供我们开发新的插件及全局注册组件等 install方法第一个参数是vue的构造器,第二个参数是可选的选项对象 export default {install(Vue,option){组件指令混入挂载vue原型} }2:注册组件 一:注册单个组件 1…...

Flutter:文件读取—— video_player、chewie、image_picker、file_picker
前言 简单学习一下几个比较好用的文件读取库 video_player 简介 用于视频播放 官方文档 https://pub-web.flutter-io.cn/packages/video_player 安装 flutter pub add video_player加载网络视频 class _MyHomePageState extends State<MyHomePage> {// 控制器late…...

vim的使用
vim文本编辑器 vim介绍命令模式光标移动选中内容复制内容粘贴内容删除撤销/恢复字符转换 编辑模式末行模式保存/退出查找行号显示文件切换 扩展 vim介绍 vim是Linux自带的文本编辑器,具有命令模式、编辑模式、末行模式三种模式。 模式间的切换: 命令模…...
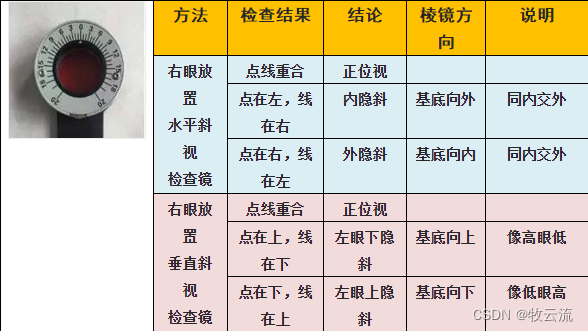
马氏杆法检查斜视
使用 检查水平向斜视时,使用水平向马氏杆检查;重直向斜视时,使用重直问马氏杆;检查旋转斜视时,使用双马氏杆. 检查水平向斜视 双眼屈光不正全矫 双眼同时打开,右眼前加水平向马氏杆,左眼前不加 双眼同时观察点光源&…...
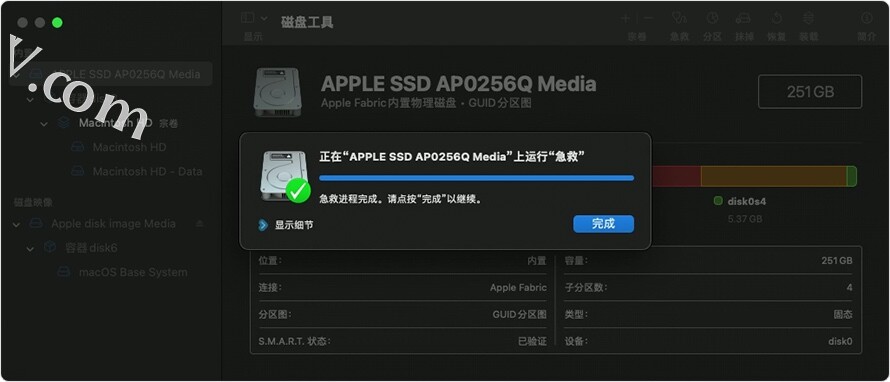
Mac电脑怎么使用“磁盘工具”修复磁盘
我们可以使用“磁盘工具”的“急救”功能来查找和修复磁盘错误。 “磁盘工具”可以查找和修复与 Mac 磁盘的格式及目录结构有关的错误。使用 Mac 时,错误可能会导致意外行为,而重大错误甚至可能会导致 Mac 彻底无法启动。 继续之前,请确保您…...
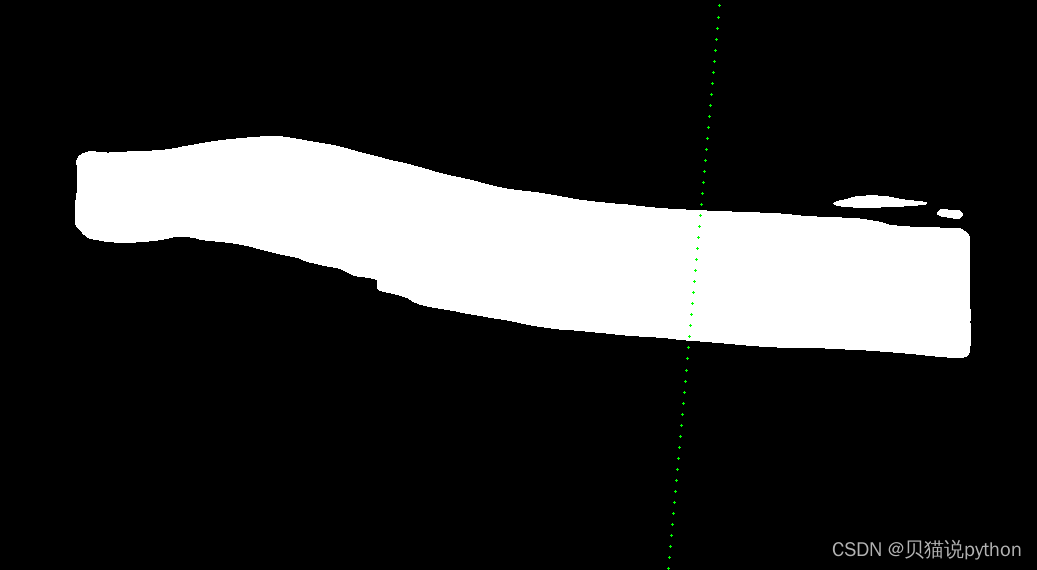
c++画出分割图像,水平线和垂直线
1、pca 找到图像某个区域的垂直线,并画出来 // 1、 斑块的框 血管二值化图,pca 找到垂直血管壁的直线, 还是根据斑块找主轴方向吧// Step 1: 提取斑块左右范围内的血管像素点坐标,std::vector<cv::Point> points;for (int y 0; y <…...
—— enumerate() 函数的用法)
Python 程序设计入门(015)—— enumerate() 函数的用法
Python 程序设计入门(015)—— enumerate() 函数的用法 目录 Python 程序设计入门(015)—— enumerate() 函数的用法一、enumerate() 函数的语法二、为可迭代对象创建索引三、将字符串、列表等转换为字典1、将字符串转换为字典2、…...

__dict__属性
__dict__ 是 Python 中的一个特殊属性,通常存在于大多数 Python 对象中,用于存储该对象的可变属性。 以下是关于 __dict__ 的一些关键点和详细信息: 存储属性:对于大多数自定义的 Python 对象,__dict__ 属性包含了这个…...
k8s之Pod控制器
目录 一、Pod控制器及其功用二、pod控制器的多种类型2.1 pod容器中的有状态和无状态的区别 三、Deployment 控制器四、SatefulSet 控制器4.1 StatefulSet由以下几个部分组成4.2 为什么要有headless?4.3 为什么要有volumeClaimTemplate?4.4 滚动更新4.5 扩…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
