图的遍历DFSBFS-有向图无向图
西江月・证明
即得易见平凡,仿照上例显然。留作习题答案略,读者自证不难。
反之亦然同理,推论自然成立。略去过程Q.E.D.,由上可知证毕。
有向图的遍历可以使用深度优先搜索(DFS)和广度优先搜索(BFS)两种算法来实现。
有向图的遍历
1.DFS遍历有向图的步骤:
- 选择一个起始节点,标记为已访问。
- 访问其邻接节点中第一个未被访问的节点,标记为已访问。
- 以该节点为起始节点,重复步骤2,直到没有未访问的邻接节点。
- 回溯到上一个节点,重复步骤2和步骤3,直到所有节点都被访问。
DFS遍历可以使用递归或栈来实现。
#include<bits/stdc++.h>
using namespace std;// 建立有向图
void build_graph(vector<vector<int>>& graph, int num_edges) {for (int i = 0; i < num_edges; i++) {int from, to;cin >> from >> to;graph[from].push_back(to);}
}// 有向图的深度优先遍历
void dfs(vector<vector<int>>& graph, int node, vector<bool>& visited, stack<int>& result) {visited[node] = true;for (int i = 0; i < graph[node].size(); i++) {int next_node = graph[node][i];if (!visited[next_node]) {dfs(graph, next_node, visited, result);}}result.push(node);
}// 输出拓扑排序结果
void print_topological_order(stack<int>& result) {while (!result.empty()) {cout << result.top() << " ";result.pop();}
}int main() {int num_nodes, num_edges;cin >> num_nodes >> num_edges;// 建立有向图vector<vector<int>> graph(num_nodes);build_graph(graph, num_edges);// 定义visited数组vector<bool> visited(num_nodes, false);// 定义结果栈stack<int> result;// 对每个未被遍历的节点进行深度优先遍历for (int i = 0; i < num_nodes; i++) {if (!visited[i]) {dfs(graph, i, visited, result);}}// 输出拓扑排序结果print_topological_order(result);return 0;
}2.BFS遍历有向图的步骤:
- 选择一个起始节点,标记为已访问,并将其加入队列。
- 从队列中取出第一个节点,访问其邻接节点中第一个未被访问的节点,标记为已访问,并将其加入队列。
- 重复步骤2,直到队列为空。
- 如果还有未访问的节点,选择其中一个作为新的起始节点,重复步骤1~3。
BFS遍历可以使用队列来实现。
#include<bits/stdc++.h>
using namespace std;void bfs(vector<vector<int>>& graph, vector<bool>& visited, int start) {queue<int> q;visited[start] = true;q.push(start);while (!q.empty()) {int curr = q.front();cout << curr << " ";q.pop();for (int neighbor : graph[curr]) {if (!visited[neighbor]) {visited[neighbor] = true;q.push(neighbor);}}}
}int main() {int n = 6; // number of nodes// adjacency list representation of the graphvector<vector<int>> graph(n);graph[0] = {1, 2};graph[1] = {0, 2, 3, 4};graph[2] = {0, 1, 3};graph[3] = {1, 2, 4};graph[4] = {1, 3, 5};graph[5] = {4};// mark all nodes as not visitedvector<bool> visited(n, false);// perform BFS traversal starting from node 0bfs(graph, visited, 0);return 0;
}无向图的遍历
无向图的遍历有两种方法:深度优先搜索(DFS)和广度优先搜索(BFS)。
1. 深度优先搜索(DFS)
深度优先搜索是一种递归的搜索方式,从一个起点出发,沿着一条路径一直往下搜索直到走到尽头,然后回溯到之前的节点,继续搜索其他未被访问的节点。具体步骤如下:
(1)访问起点节点,并将其标记为已访问。
(2)从起点节点出发,搜索与其直接相邻的未被访问的节点。
(3)如果找到了一个未被访问的节点,就继续以该节点为起点递归搜索,直到无法再继续搜索为止。
(4)当所有与当前节点直接相邻的节点都被访问过,回溯到之前的节点,继续搜索其他未被访问的节点。
(5)重复上述步骤,直到所有节点都被访问过。
#include<bits/stdc++.h>
using namespace std;void dfs(int u, vector<bool>& visited, vector<vector<int>>& adjList) {visited[u] = true; // 标记节点u为已访问cout << u << " "; // 输出节点u// 遍历所有与节点u相邻的节点for (int v : adjList[u]) {if (!visited[v]) {dfs(v, visited, adjList); // 递归访问节点v}}
}void dfsTraversal(int n, vector<vector<int>>& adjList) {vector<bool> visited(n + 1, false); // 初始化所有节点为未访问状态for (int i = 1; i <= n; i++) {if (!visited[i]) { // 如果节点i未被访问过,从节点i开始DFS遍历dfs(i, visited, adjList);}}
}int main() {int n, m;cin >> n >> m; // 读入节点数和边数vector<vector<int>> adjList(n + 1); // 邻接表for (int i = 1; i <= m; i++) {int u, v;cin >> u >> v; // 读入一条边的两个端点adjList[u].push_back(v);adjList[v].push_back(u); // 无向图,所以需要两条边}dfsTraversal(n, adjList); // DFS遍历return 0;
}
2. 广度优先搜索(BFS)
广度优先搜索是一种迭代的搜索方式,从一个起点出发,依次访问其所有相邻的节点,并将这些节点加入一个队列中,在队列中按照先进先出的顺序继续访问队列中的节点,直到队列为空为止。具体步骤如下:
(1)访问起点节点,并将其标记为已访问。
(2)将起点节点放入一个队列中。
(3)从队列中取出第一个节点,并访问其所有未被访问的相邻节点,并将这些节点加入队列中。
(4)重复步骤(3),直到队列为空为止。
(5)所有被访问过的节点组成了图的遍历。
#include<bits/stdc++.h>
using namespace std;void bfs(vector<vector<int>>& graph, vector<bool>& visited, int start) {queue<int> q;visited[start] = true;q.push(start);while (!q.empty()) {int curr = q.front();cout << curr << " ";q.pop();for (int neighbor : graph[curr]) {if (!visited[neighbor]) {visited[neighbor] = true;q.push(neighbor);}}}
}int main() {int n = 6; // number of nodes// adjacency list representation of the graphvector<vector<int>> graph(n);graph[0] = {1, 2};graph[1] = {0, 2, 3, 4};graph[2] = {0, 1, 3};graph[3] = {1, 2, 4};graph[4] = {1, 3, 5};graph[5] = {4};// mark all nodes as not visitedvector<bool> visited(n, false);// perform BFS traversal starting from node 0bfs(graph, visited, 0);return 0;
}
相关文章:

图的遍历DFSBFS-有向图无向图
西江月・证明 即得易见平凡,仿照上例显然。留作习题答案略,读者自证不难。 反之亦然同理,推论自然成立。略去过程Q.E.D.,由上可知证毕。 有向图的遍历可以使用深度优先搜索(DFS)和广度优先搜索(…...
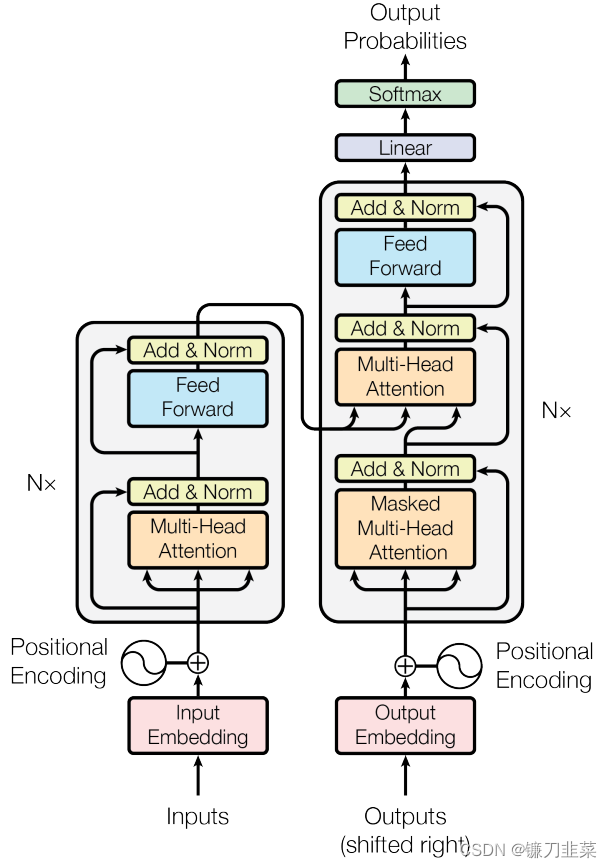
【NLP】深入浅出全面回顾注意力机制
深入浅出全面回顾注意力机制 1. 注意力机制概述2. 举个例子:使用PyTorch带注意力机制的Encoder-Decoder模型3. Transformer架构回顾3.1 Transformer的顶层设计3.2 Encoder与Decoder的输入3.3 高并发长记忆的实现self-attention的矩阵计算形式多头注意力(…...

Linux应用编程的read函数和Linux驱动编程的read函数的区别
Linux应用编程的read函数用于从文件描述符(文件、管道、套接字等)中读取数据。它的原型如下: ssize_t read(int fd, void *buf, size_t count);其中,fd参数是文件描述符,buf是用于存储读取数据的缓冲区,co…...
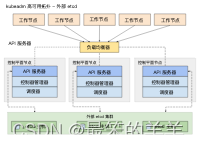
Kubernetes(K8s)从入门到精通系列之十:使用 kubeadm 创建一个高可用 etcd 集群
Kubernetes K8s从入门到精通系列之十:使用 kubeadm 创建一个高可用 etcd 集群 一、etcd高可用拓扑选项1.堆叠(Stacked)etcd 拓扑2.外部 etcd 拓扑 二、准备工作三、建立集群1.将 kubelet 配置为 etcd 的服务管理器。2.为 kubeadm 创建配置文件…...

使用动态规划实现错排问题-2023年全国青少年信息素养大赛Python复赛真题精选
[导读]:超平老师计划推出《全国青少年信息素养大赛Python编程真题解析》50讲,这是超平老师解读Python编程挑战赛真题系列的第15讲。 全国青少年信息素养大赛(原全国青少年电子信息智能创新大赛)是“世界机器人大会青少年机器人设…...

大规模向量检索库Faiss学习总结记录
因为最近要使用到faiss来做检索和查询,所以这里只好抽出点时间来学习下,本文主要是自己最近学习的记录,来源于网络资料查询总结,仅用作个人学习总结记录。 Faiss的全称是Facebook AI Similarity Search,是FaceBook的A…...
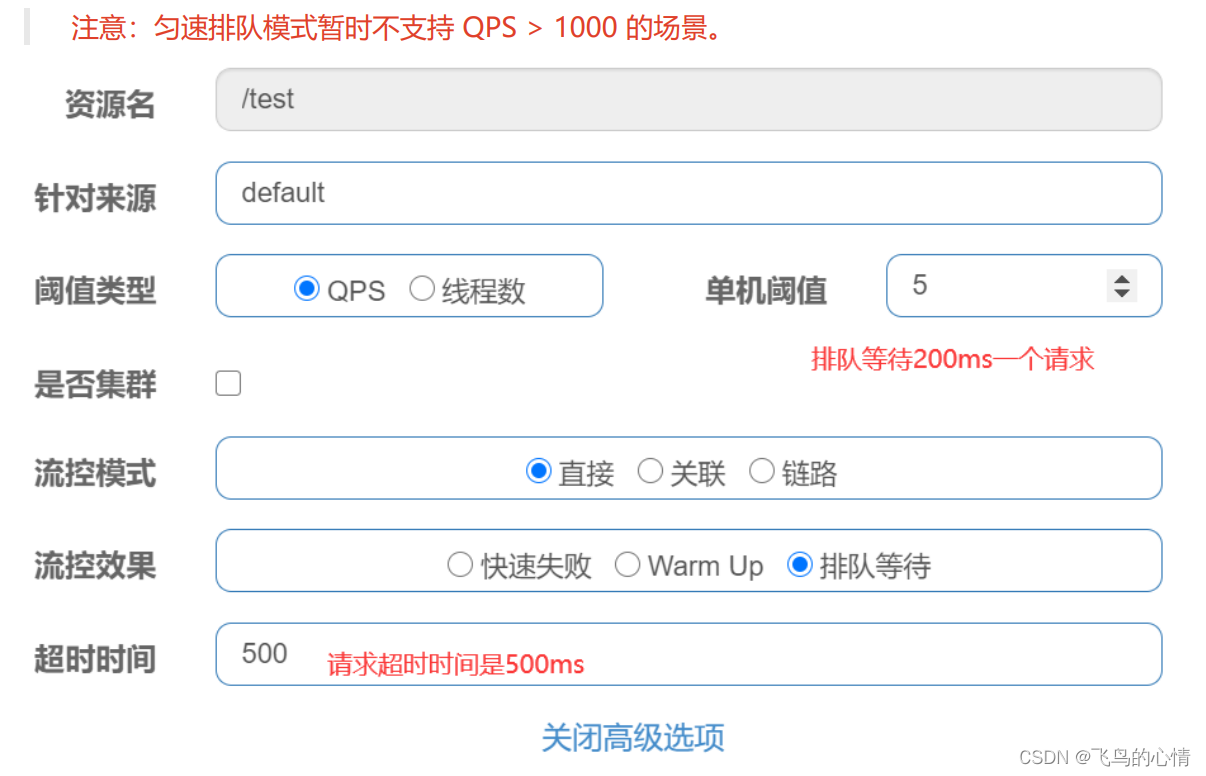
SpringCloudAlibaba之Sentinel(一)流控篇
前言: 为什么使用Sentinel,这是一个高可用组件,为了使我们的微服务高可用而生 我们的服务会因为什么被打垮? 一,流量激增 缓存未预热,线程池被占满 ,无法响应 二,被其他服务拖…...

哪种模式ip更适合你的爬虫项目?
作为一名爬虫程序员,对于数据的采集和抓取有着浓厚的兴趣。当谈到爬虫ip时,你可能会听说过两种常见的爬虫ip类型:Socks5爬虫ip和HTTP爬虫ip。但到底哪一种在你的爬虫项目中更适合呢?本文将帮助你进行比较和选择。 首先,…...
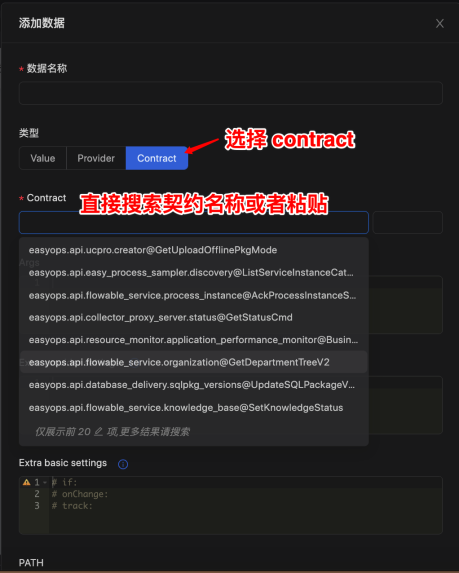
优维低代码实践:对接数据
优维低代码技术专栏,是一个全新的、技术为主的专栏,由优维技术委员会成员执笔,基于优维7年低代码技术研发及运维成果,主要介绍低代码相关的技术原理及架构逻辑,目的是给广大运维人提供一个技术交流与学习的平台。 优维…...

docker 离线模式-部署容器
有网络的情况下下载需要的镜像 比如(下面以tomcat为例子,其他镜像类似) docker pull tomcat打包镜像文件到本地 docker save tomcat -o tomcat.tar将tomcat.tar 上传到内网服务器(无外网环境) 导入镜像 docker load -i tomcat.tar创建容器…...

MDN-HTTP
参考资料 文章目录 HTTP简介HTTP 和 HTTPSHTTP消息典型的HTTP会话HTTP响应状态HTTP安全HTTP CookieHTTP压缩 HTTP简介 HTTP(Hypertext Transfer Protocol)是一种用于在计算机网络中传输超文本和其他资源的应用层协议。他是互联网的基础协议之一&#x…...

【数据库】PostgreSQL中使用`SELECT DISTINCT`和`SUBSTRING`函数实现去重查询
在PostgreSQL中,我们可以使用SELECT DISTINCT和SUBSTRING函数来实现对某个字段进行去重查询。本文将介绍如何使用这两个函数来实现对resource_version字段的去重查询。 1. SELECT DISTINCT语句 SELECT DISTINCT语句用于从表中选择不重复的记录。如果没有指定列名&…...
笔记本WIFI连接无网络【实测有效,不用重启电脑】
笔记本Wifi连接无网络实测有效解决方案 问题描述: 笔记本买来一段时间后,WIFI网络连接开机一段时间还正常连接,但是过一段时间显示网络连接不上,重启电脑太麻烦,选择编写重启网络脚本解决。三步解决问题。 解决方案&a…...
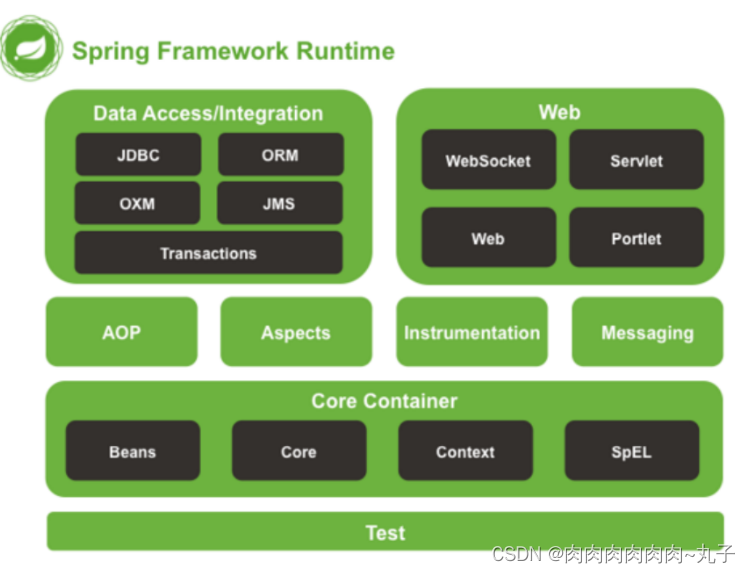
Java课题笔记~ Spring 概述
Spring 框架 一、Spring 概述 1、Spring 框架是什么 Spring 是于 2003 年兴起的一个轻量级的 Java 开发框架,它是为了解决企业应用开发的复杂性而创建的。Spring 的核心是控制反转(IoC)和面向切面编程(AOP)。 Spring…...
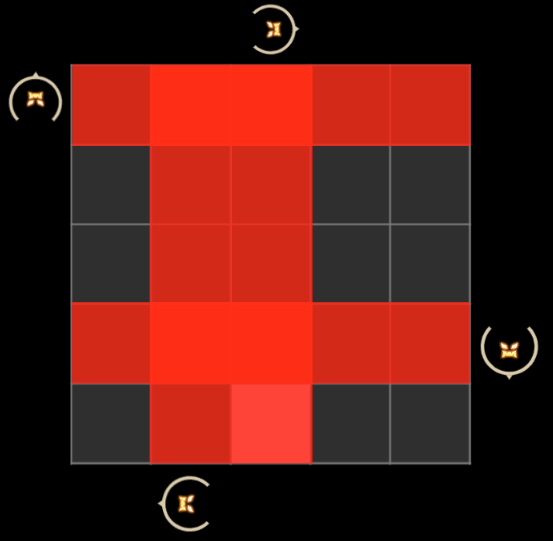
2022 robocom 世界机器人开发者大赛-本科组(国赛)
RC-u1 智能红绿灯 题目描述: RC-u1 智能红绿灯 为了最大化通行效率同时照顾老年人穿行马路,在某养老社区前,某科技公司设置了一个智能红绿灯。 这个红绿灯是这样设计的: 路的两旁设置了一个按钮,老年人希望通行马路时会…...

【雕爷学编程】Arduino动手做(195)---HT16k33 矩阵 8*8点阵屏模块6
37款传感器与模块的提法,在网络上广泛流传,其实Arduino能够兼容的传感器模块肯定是不止37种的。鉴于本人手头积累了一些传感器和执行器模块,依照实践出真知(一定要动手做)的理念,以学习和交流为目的&#x…...

Typescript]基础篇之 tsc 命令解析
[Typescript]基础[TOC]([Typescript]基础篇之 tsc 命令解析 tsc 命令概览编译参数说明--declaration--watch 这里是对 tsc 的一个详细介绍 tsc 命令概览 安装 Typescript 后可以使用 tsc 编译 ts 文件,tsc 命令是否支持其它参数 如果需要查看 tsc 支持的命令,或者…...
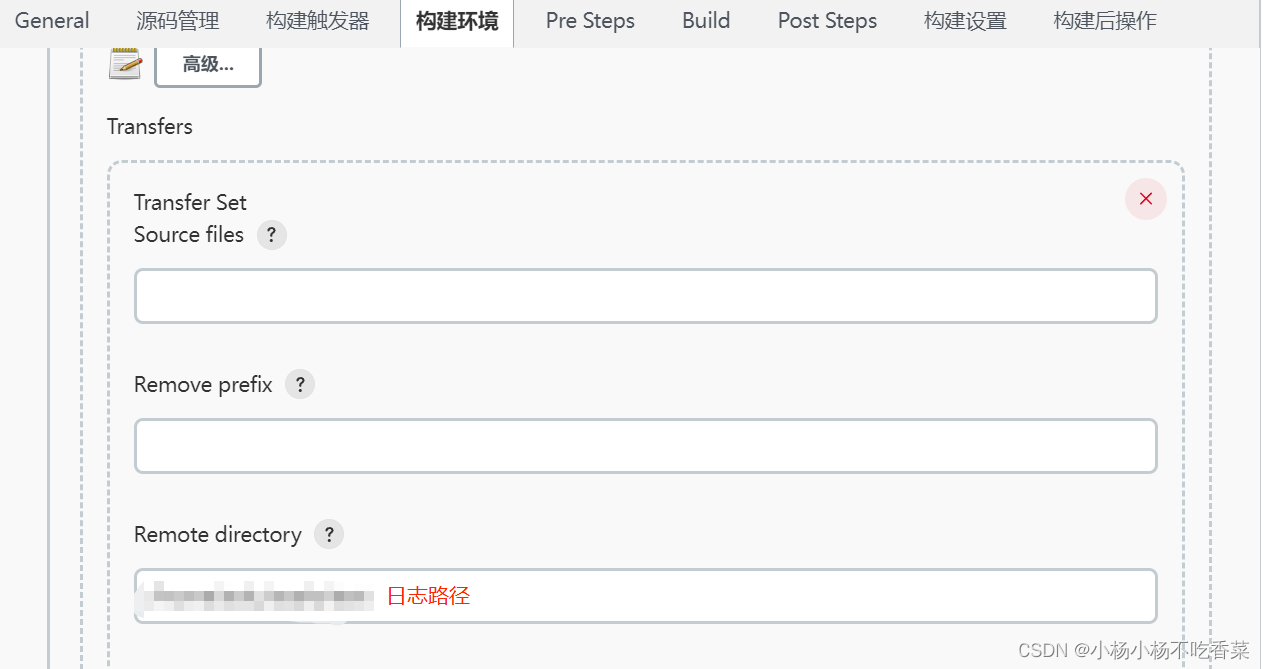
测试人员简单使用Jenkins
一、测试人员使用jenkins干什么? 部署测试环境 二、相关配置说明 一般由开发人员进行具体配置 1.Repository URL:填写git地址 2.填写开发分支,测试人员可通过相应分支进行测试环境的构建部署 当多个版本并行时,开发人员可以通过…...
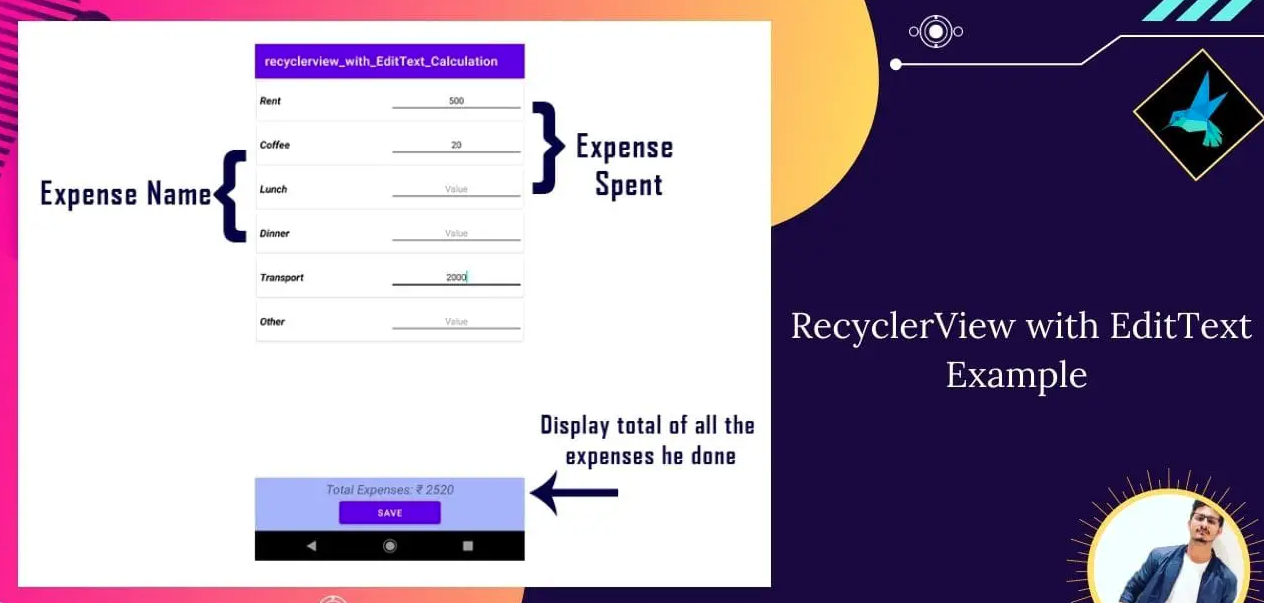
使用RecyclerView构建灵活的列表界面
使用RecyclerView构建灵活的列表界面 1. 引言 在现代移动应用中,列表界面是最常见的用户界面之一,它能够展示大量的数据,让用户可以浏览和操作。无论是社交媒体的动态流、商品展示、新闻列表还是任务清单,列表界面都扮演着不可或…...

linux ubuntu安装mysql
在 Ubuntu 上安装 MySQL 的步骤如下: 更新系统软件包列表: sudo apt update 安装 MySQL 服务器: sudo apt install mysql-server 安装完成,可以使用以下命令检查 MySQL 服务器是否正在运行: sudo systemctl status mysql 如果 MyS…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
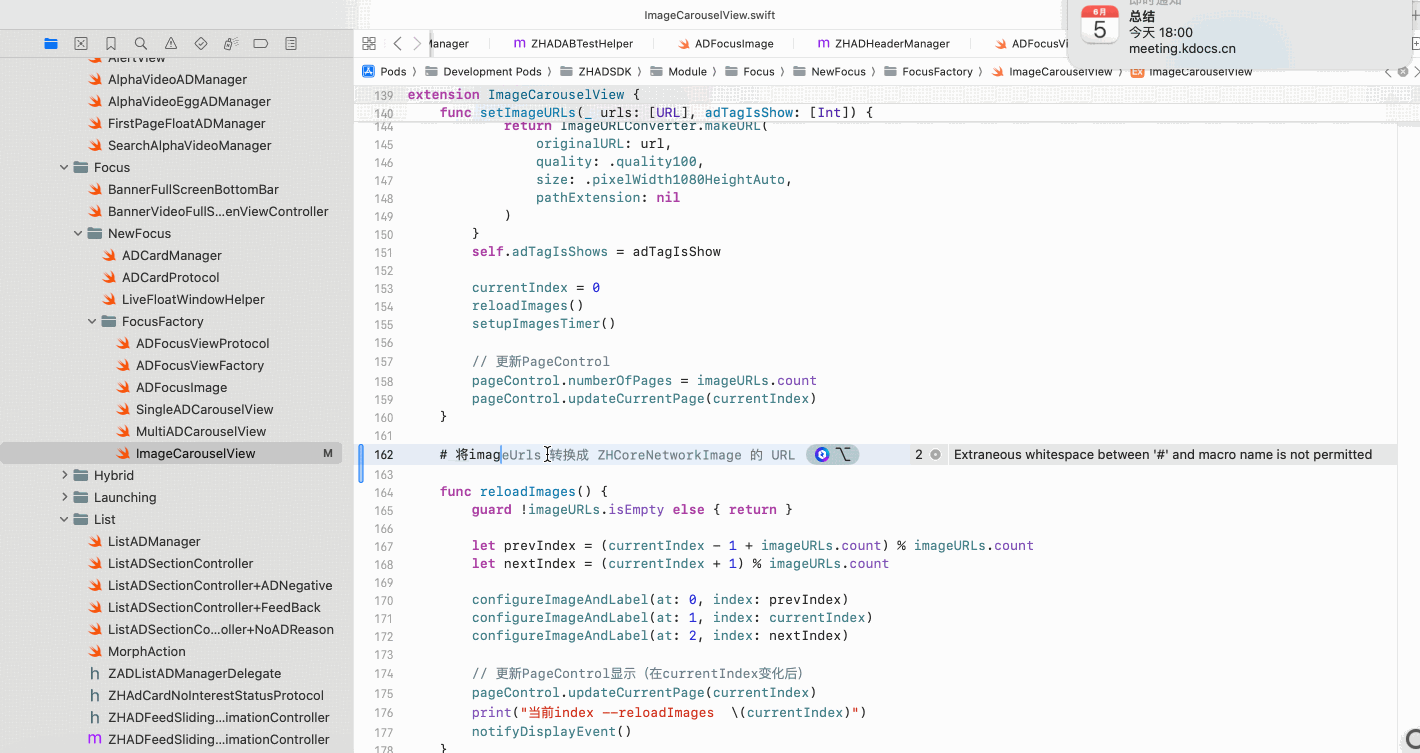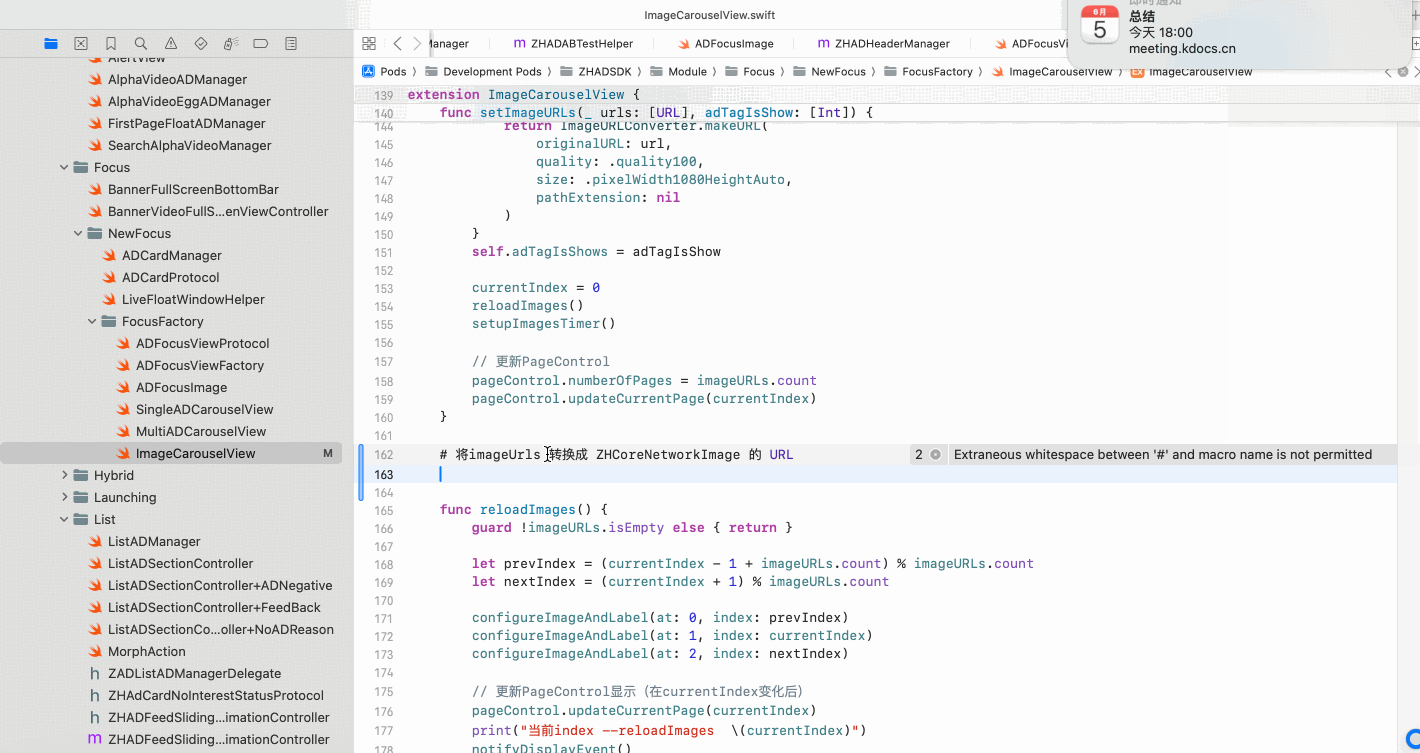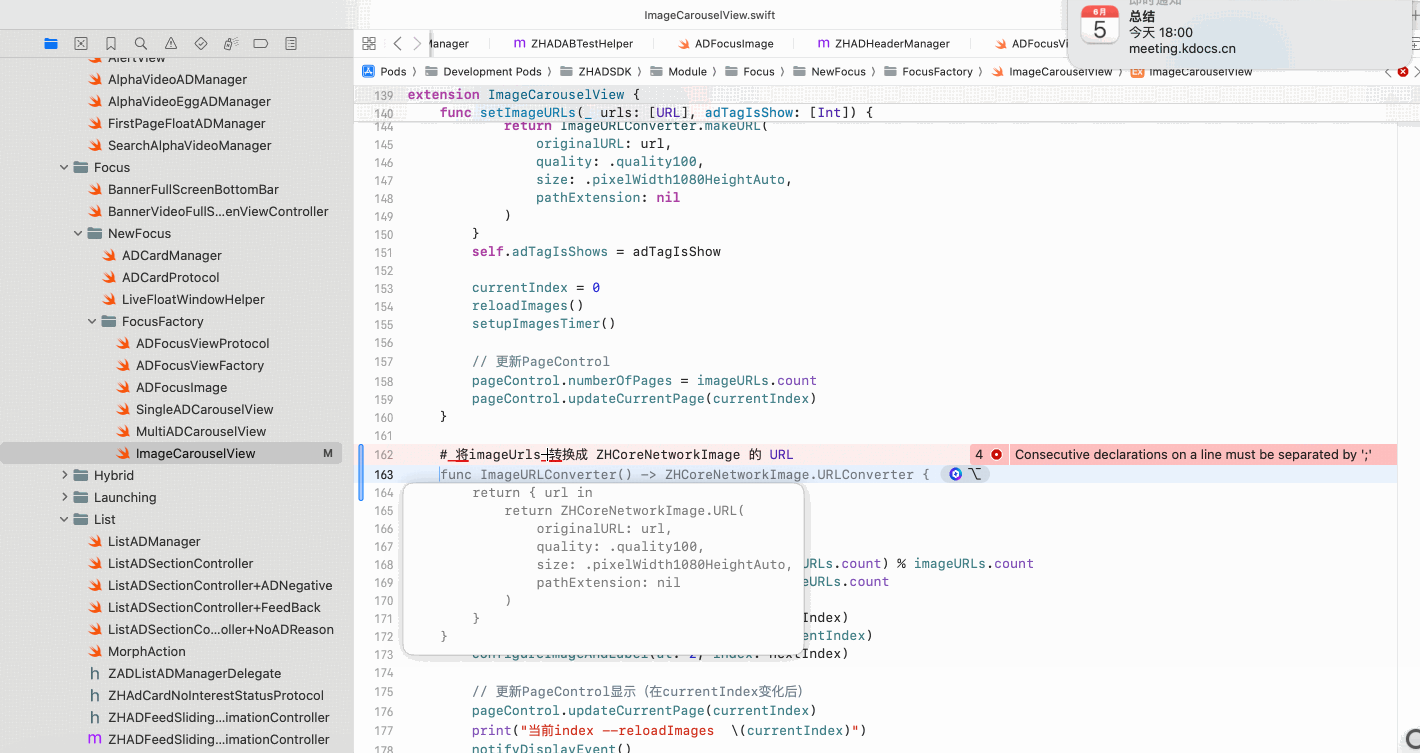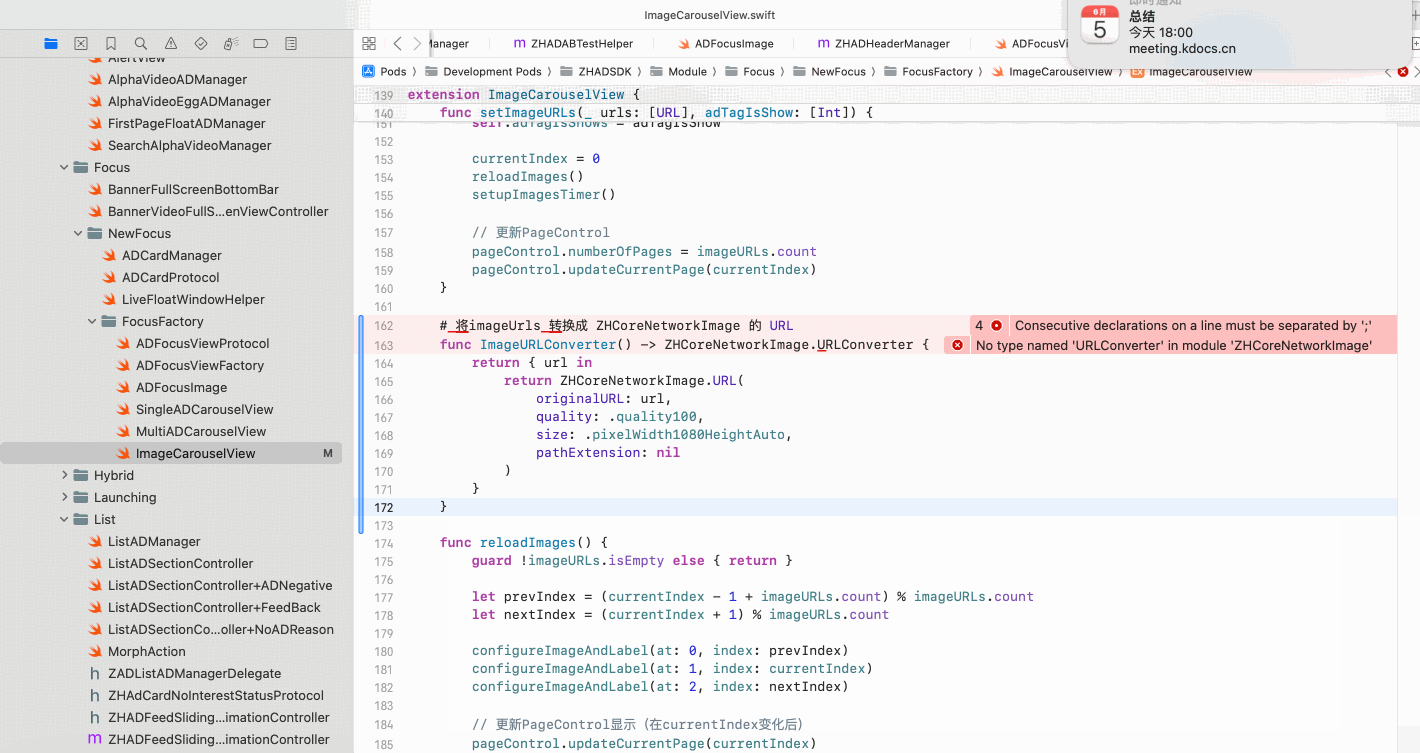
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...
