【学习笔记】NOIP暴零赛3
博弈(game)
观察到博弈过程中胜负态不会发生改变,那么求出从每个棋子出发能走的最长链,然后背包即可。
复杂度O(nm)O(nm)O(nm)。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int mod=998244353;
const int N=305;
int n,m,dp[N],in[N],g[N*N],g2[N*N],vis[N];
ll res;
string s;
queue<int>Q;
vector<int>ve[N];
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n>>m>>s;for(int i=1;i<=m;i++){int u,v;cin>>u>>v,u--,v--;if(u>v)swap(u,v);ve[v].pb(u),in[u]++;}for(int i=0;i<n;i++)if(!in[i])Q.push(i);while(Q.size()){int u=Q.front();Q.pop();for(auto v:ve[u]){if(--in[v]==0)Q.push(v);if(s[u]==s[v])dp[v]=max(dp[v],dp[u]+1),vis[v]=1;else if(s[u]!=s[v]&&!vis[u]&&!dp[u])dp[v]=max(dp[v],1);}}g[0]=g2[0]=1;for(int i=0;i<n;i++){if(s[i]=='W'){for(int j=n*n;j>=dp[i];j--){g[j]=(g[j]+g[j-dp[i]])%mod;}}else{for(int j=n*n;j>=dp[i];j--){g2[j]=(g2[j]+g2[j-dp[i]])%mod;}}}for(int i=1;i<=n*n;i++){g2[i]=(g2[i-1]+g2[i])%mod;}for(int i=1;i<=n*n;i++){res=(res+(ll)g[i]*g2[i-1])%mod;}cout<<res;
}
排列 (perm)
神仙题。
考虑怎么转化这个性质。等价于,不能存在一个区间,里面同时存在(a,b),(b,c)(a,b),(b,c)(a,b),(b,c)而不存在(a,c)(a,c)(a,c)。
由此可以想到传递闭包:每个区间,如果建一个图,就都必须具有传递性。
然后我们发现,只需要每个前缀都有传递性,每个后缀都有传递性就好了。
不要问我怎么想到的,以及证明,国内谜语人太多了,可以去骂写题解的人
也就是说,任取一个iii,设GiG_iGi为考虑前iii条边组成的图,那么GiG_iGi和GiG_iGi的补图都有传递性。
有一个很神奇的结论:满足这样条件的GGG恰好有n!n!n!个,这是因为,任取一个排列ppp,如果a<ba<ba<b并且aaa在ppp中的位置在bbb的后面,那么连边(a,b)(a,b)(a,b),这样构造出来的图一定是满足传递性的,并且这是一个双射。
可能打表反而更实际一些
然后,最无脑的想法是,因为合法的前缀只有n!n!n!个,所以状态数只有O(n!)O(n!)O(n!),也就是说可以直接把整张图的每条边存起来,然后暴力转移。不过既然我们都知道这样的GGG和一个排列ppp构成双射了,那么在ppp中转移则显得合情合理,一个合法的GGG加入一条边(a,b)(a,b)(a,b)后仍然合法,当且仅当GGG对应的排列ppp中aaa恰好在bbb前面的位置,加入边(a,b)(a,b)(a,b)相当于是交换(a,b)(a,b)(a,b)的位置。
复杂度O(n!×n)O(n!\times n)O(n!×n)。
对不起代码咕掉了,因为感受到了出题人的恶意
另外,这题的想法也太聪明了吧。。。
考场上只写了20pts20pts20pts的暴搜,大概是因为被搞心态了所以没想到40pts40pts40pts的无脑状压dpdpdp,不过这种失分还是挺无语的
出题人你还是要有同理心啊
子段和 (seg)
放在t3t3t3其实还是比较水的。
直接用数据结构暴力维护就能做到O(n2logw)O(n^2\log w)O(n2logw),可以得到70pts70pts70pts。
然而没写对拍结果写炸了,警钟长鸣
接下来一步应该容易想到:对于max\maxmax相同的区间,我们每次要取出min\minmin最小的那一个,对于这个过程,我们可以用一个set\text{set}set来维护。考虑堆套set\text{set}set,堆里面每个元素维护区间max\maxmax相同的区间的集合,用set\text{set}set维护这些区间的最小值的位置。这里有一个比较巧妙的想法,就是把堆中的元素存在一个数组里,这样每次从堆中取元素时就不用把它复制一遍了。
复杂度O(nlogn)O(n\log n)O(nlogn)。
后来发现题解的思路确实更加聪明。
考虑给定kkk,怎么求g(k)g(k)g(k)呢,二分答案www,令aaa为给出序列的前缀和,a0=0a_0=0a0=0,每次操作就是对一段后缀−1-1−1,最后要使得∀i<j,aj−ai≤w\forall i<j,a_j-a_i\le w∀i<j,aj−ai≤w。
直接从前往后贪心,维护一个lim\text{lim}lim表示后面的aaa经过操作后都不能超过lim\text{lim}lim。如果ai>lima_i>\text{lim}ai>lim那么就在这里执行ai−lima_i-\text{lim}ai−lim次操作,得到新的aaa。然后令lim:=min(lim,ai+w)\text{lim}:=\min(\text{lim},a_i+w)lim:=min(lim,ai+w)。
正解非常脑洞。考虑直接把所有www的lim\text{lim}lim一起维护,设这个函数为L(w)L(w)L(w),另外维护A(w)A(w)A(w)表示目前的代价。剩下的就是用数据结构大力乱搞。
先贴一个70pts70pts70pts的代码吧。原谅我没有能力刚正解。
毕竟quack也说了这题到这里就差不多了。。。
#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
const int mod=998244353;
int n,p[200005][20],p2[200005][20],Log[200005];
ll a[200005],s[200005],Min[200005][20],Max[200005][20],K,res,inv2=(mod+1)/2;
vector<pair<ll,ll>>v;
int qmin(int l,int r){int k=Log[r-l+1];return (Min[l][k]<Min[r-(1<<k)+1][k])?p[l][k]:p[r-(1<<k)+1][k];
}
int qmax(int l,int r){int k=Log[r-l+1];return (Max[l][k]>Max[r-(1<<k)+1][k])?p2[l][k]:p2[r-(1<<k)+1][k];
}
struct node{int l,r;ll S;bool operator <(const node &a)const{return s[qmax(l,r)]-S<s[qmax(a.l,a.r)]-a.S;}
};
priority_queue<node>q;
vector<node>vec;
ll Sum(ll l,ll r){l%=mod,r%=mod;return (r-l+1)*(l+r)%mod*inv2%mod;
}
void calc(ll &K,ll Max,ll x,ll y){if(K/x>=y){res+=Sum(Max-y+1,Max)*(x%mod)-y;res%=mod,K-=x*y;}else{res+=Sum(Max-K/x+1,Max)*(x%mod)-(K/x),res%=mod;Max-=K/x,K%=x,res+=(K%mod)*(Max%mod),res%=mod,K=0;}
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=2;i<=n;i++)Log[i]=Log[i/2]+1;for(int i=1;i<=n;i++){cin>>a[i],s[i]=max(s[i-1]+a[i],0ll),Min[i][0]=Max[i][0]=s[i],p[i][0]=p2[i][0]=i;}for(int j=1;j<20;j++){for(int i=1;i<=n-(1<<j)+1;i++){Min[i][j]=min(Min[i][j-1],Min[i+(1<<j-1)][j-1]),Max[i][j]=max(Max[i][j-1],Max[i+(1<<j-1)][j-1]);p[i][j]=(Min[i][j]==Min[i][j-1])?p[i][j-1]:p[i+(1<<j-1)][j-1],p2[i][j]=(Max[i][j]==Max[i][j-1])?p2[i][j-1]:p2[i+(1<<j-1)][j-1]; }}q.push({1,n,0});cin>>K;while(q.size()){ll MAX=s[qmax(q.top().l,q.top().r)]-q.top().S,S2(inf);vec.clear();if(!MAX)break;while(q.size()&&s[qmax(q.top().l,q.top().r)]-q.top().S==MAX){int l=q.top().l,r=q.top().r;ll S=q.top().S;q.pop();S2=min(S2,s[qmin(l,r)]-S),vec.pb({l,r,S});}if(q.size())S2=min(S2,MAX-(s[qmax(q.top().l,q.top().r)]-q.top().S));for(int i=0;i<vec.size();i++){int l=vec[i].l,r=vec[i].r,p=qmin(l,r);ll S=vec[i].S;if(s[p]-S-S2==0){if(p>l)q.push({l,p-1,S+S2});if(p<r)q.push({p+1,r,S+S2});}else q.push({l,r,S+S2});}calc(K,MAX,vec.size(),S2);if(!K)break;}if(K){for(int i=1;i<=n;i++)a[i]=min(a[i],0ll);sort(a+1,a+1+n),reverse(a+1,a+1+n);for(int i=2;i<=n;i++){calc(K,a[i-1],i-1,a[i-1]-a[i]);if(!K)break;}if(K){calc(K,a[n],n,inf);}}cout<<(res+mod)%mod;
}
相关文章:

【学习笔记】NOIP暴零赛3
博弈(game) 观察到博弈过程中胜负态不会发生改变,那么求出从每个棋子出发能走的最长链,然后背包即可。 复杂度O(nm)O(nm)O(nm)。 #include<bits/stdc.h> #define ll long long #define pb push_back using namespace std; const int mod9982443…...

Java JSR规范列表
Java JSR规范列表目录概述需求:设计思路实现思路分析1.JSR2.JSR方法3.web service4.Webservice:5.数据处理器拓展实现参考资料和推荐阅读Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,m…...

Java必备小知识点1
Java程序类型: Applications和AppletApplications:是指在计算机操作系统中运行的程序。是完整的程序,能独立运行。被编译后,用普通的Java解释器就可以使其边解释边执行。必定含有一个main方法,程序执行时,首先寻找main方法&#x…...

JavaScript作用域、闭包
文章目录作用域、作用域链作用域作用域链循环中的作用域自由变量、闭包自由变量闭包的定义、表现、应用如何确定在闭包中获取正确的变量总结作用域、作用域链 作用域 编程语言中存储、访问、修改变量当中的值是一项基本能力、存储变量、访问变量必须按照一定的规则࿰…...
 对象)
JavaScript Date(日期) 对象
JavaScript Date 对象是 JavaScript 中用于处理日期和时间的内置对象。它可以用于获取当前时间、设置日期和时间、计算日期和时间之间的差异、以及将日期和时间格式化为各种字符串格式。在本文中,我们将详细介绍 JavaScript Date 对象的作用和在实际工作中的用途。 …...

rust过程宏 proc-macro-workshop解题-4-sorted
名字版本号rust1.69.0OSubuntu 22.04这一大关卡介绍的是属性式过程宏。 第一关:01-parse-enum 还是简单的看我们是否已经实现了一个属性式过程宏的空架子,如果有这个空架子,就直接通过了。 use proc_macro::TokenStream; use proc_macro2; use syn;#[proc_macro_attribut…...
数据结构与算法—队列
队列 队列介绍 有序列表,可以用数组或者链表实现。遵循先进先出原则。 数组实现队列 public class ArrayQueue {public static void main(String[] args) {ArrayQueue queue new ArrayQueue(3);// 接收用户输入char key ;Scanner sc new Scanner(System.in);…...

AcWing3416.时间显示——学习笔记
目录 题目 代码 AC结果 思路 关键步骤 题目 3416. 时间显示 - AcWing题库https://www.acwing.com/problem/content/description/3419/ 代码 import java.util.Scanner;public class Main {public static void main(String[] args){Scanner input new Scanner(System.in…...

贴吧手机端防删图GIF动态图制作解析
贴吧存活 思路技术运气 1:防删图不是存活的绝对因素,除了防删图,还有账号,ip,内容,吧的问题 2:一个图不是每个吧都可以发 3:一个贴不被删不仅仅看图片 4:有时候运气也很…...
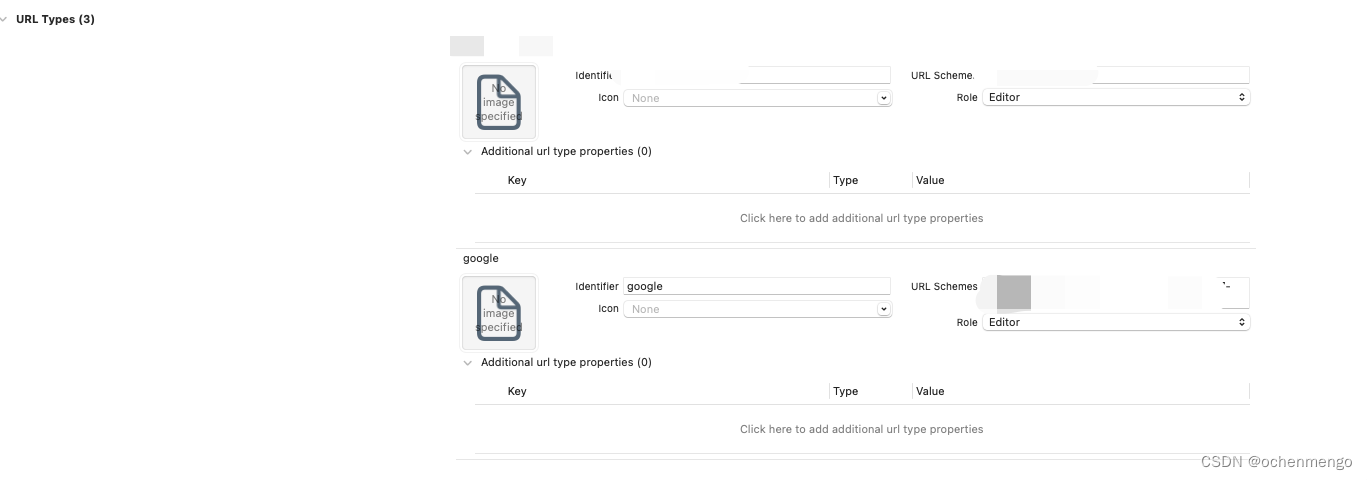
iOS接入Google登录
1.在Google Cloud后台配置客户端ID 首先要在 Google Cloud 中创建一个项目。新创建的Project需要先配置同意屏幕。一共有4步骤需要配置。 1.OAuth 同意屏幕 User Type选择"外部"进行创建。填写必必要的信息,应用名称、用户支持电子邮件地址、开发者电子邮…...

【C语言】大小端字节序问题
一、大小端字节序问题 大小端是由CPU决定的,大小端可以理解为字节顺序,所以大小端全称叫大端字节序、小端字节序。其实大端、小端这两个词是从《格列佛游记》里出来的。《格列佛游记》有一段讲的是吃鸡蛋是从大的那头敲开还是小的那头敲开的问题…...
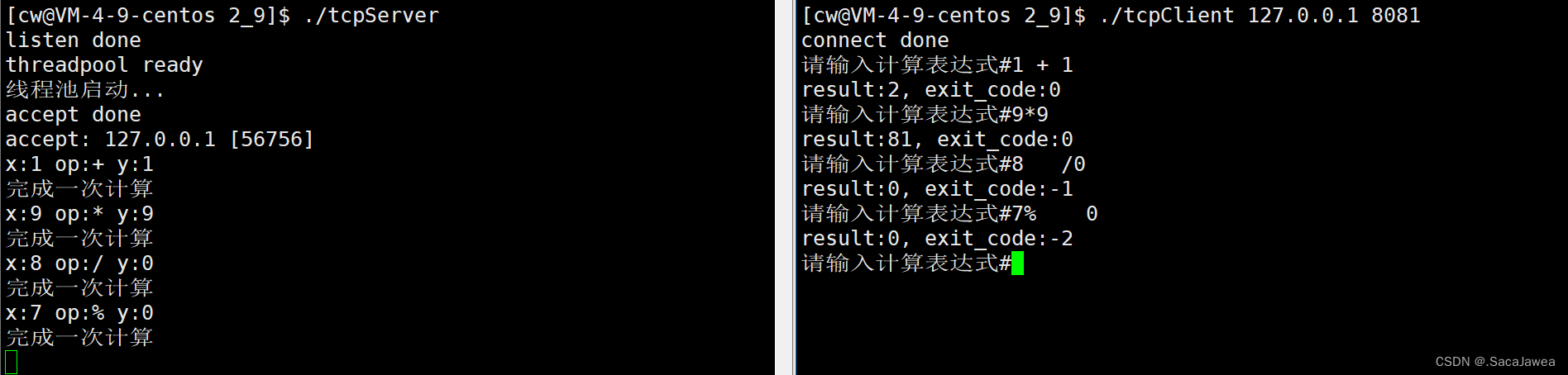
Linux | 网络通信 | 序列化和反序列化的讲解与实现
文章目录为什么要序列化?协议的实现服务端与客户端代码实现为什么要序列化? 由于默认对齐数的不同,不同的平台对相同数据进行内存对齐后,可能得到不同的数据。如果直接将这些数据进行网络传输,对方很可能无法正确的获…...
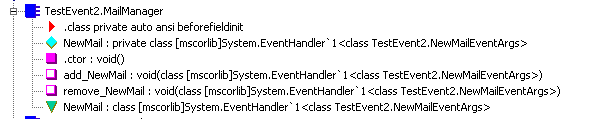
C#的委托原理刨析and事件原理刨析和两者的比较
什么是委托委托是一种引用类型,表示对具有特定参数列表和返回类型的方法的引用。 在实例化委托时,你可以将其实例与任何具有兼容参数和返回类型的方法进行绑定。 你可以通过委托实例调用方法。简单的理解,委托是方法的抽象类,它定…...
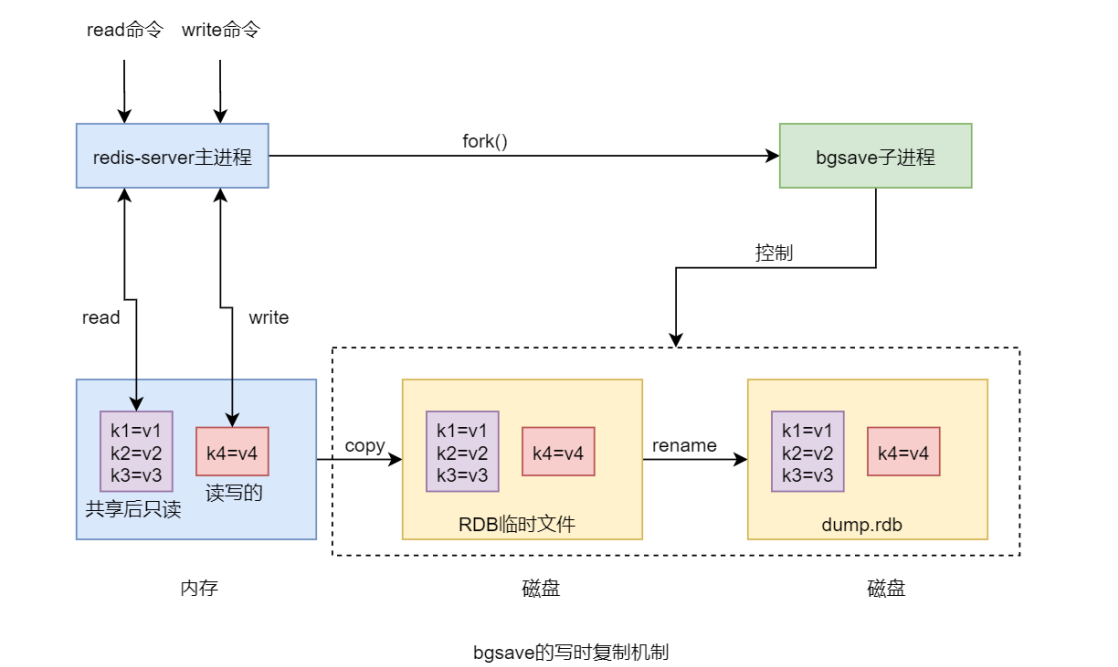
Redis学习【8】之Redis RDB持久化
文章目录Redis 持久化1 持久化基本原理2 RDB(Redis DataBase) 持久化2.1 持久化的执行2.2 手动 save 命令2.3 手动 bgsave 命令2.4 自动条件触发2.5 查看持久化时间3 RDB 优化配置3.1 save3.2 stop-write-on-bgsave-error3.3 rdbcompression3.4 rdbchecksum3.5 sanitize-dump-p…...
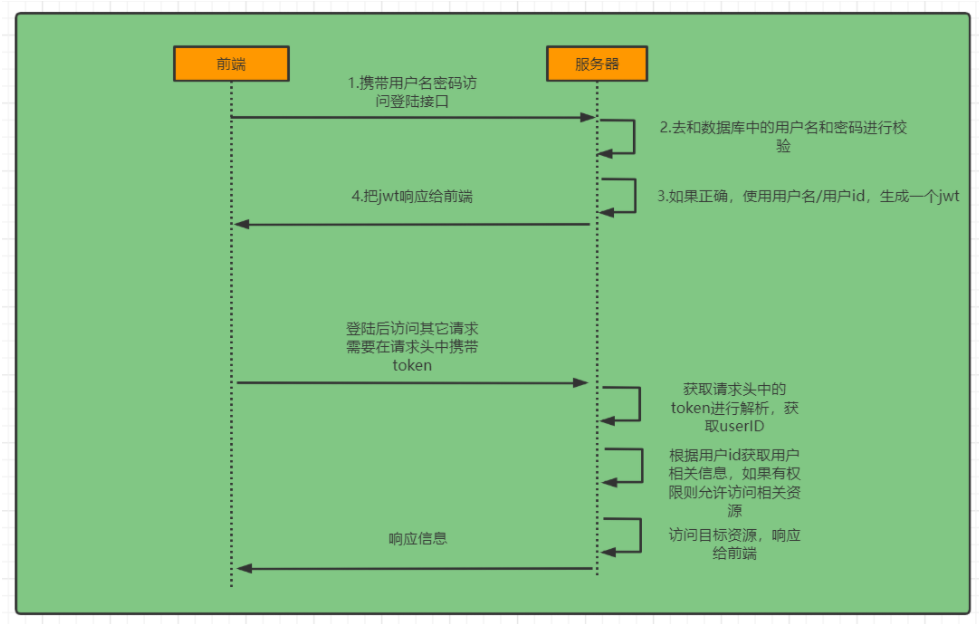
SpringSecurity认证
文章目录登陆校验流程依赖yaml实现建表、工具类、实体类加密器、AuthenticationManager登录逻辑登录过滤器、配置过滤器登出登陆校验流程 认证 登录: ①自定义登录接口 调用ProviderManager的方法进行认证 如果认证通过生成token,根据userId把用…...

Socket套接字
概念 Socket套接字,是由系统提供用于网络通信的技术,是基于TCP/IP协议的网络通信的基本操作单元。基于Socket套接字的网络程序开发就是网络编程。 分类 Socket套接字主要针对传输层协议划分为如下三类: 流套接字:使用传输层TCP…...

mysql详解之innoDB
索引 Mysql由索引组织,所以索引是mysql多重要概念之一。 聚簇索引 InnoDB和MyISAm一样都是采用B树结构,但不同点在于InnoDB是聚簇索引(或聚集索引),将数据行直接放在叶子节点后面。 这里可能存在一个误区࿱…...

电信运营商的新尝试:探索非通信领域的发展
近年来,随着电信运营商竞争的日趋激烈和网络建设的成本不断攀升,许多电信运营商已经开始缩减IT投资。然而,在如此情况下,电信运营商仍然需要寻找新的增长机会。那么,在持续缩减IT投资的情况下,电信运营商可…...

第07章_单行函数
第07章_单行函数 讲师:尚硅谷-宋红康(江湖人称:康师傅) 官网:http://www.atguigu.com 1. 函数的理解 1.1 什么是函数 函数在计算机语言的使用中贯穿始终,函数的作用是什么呢?它可以把我们经…...
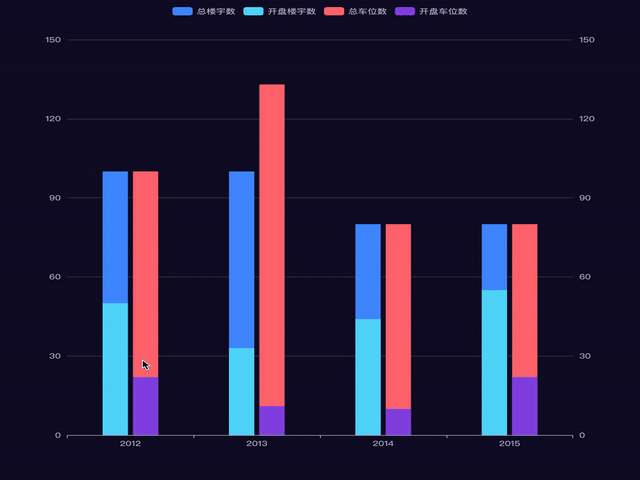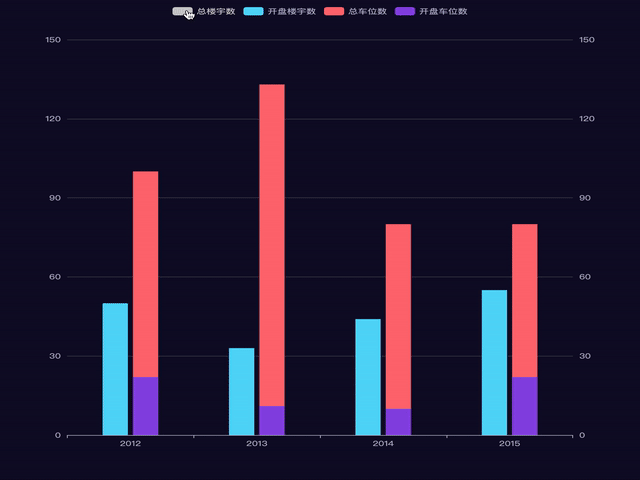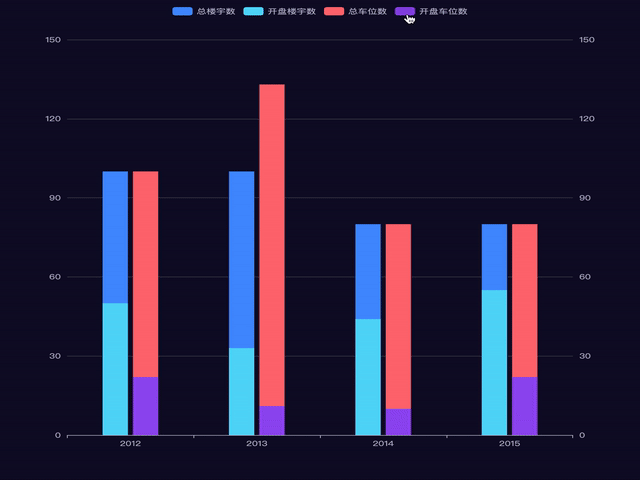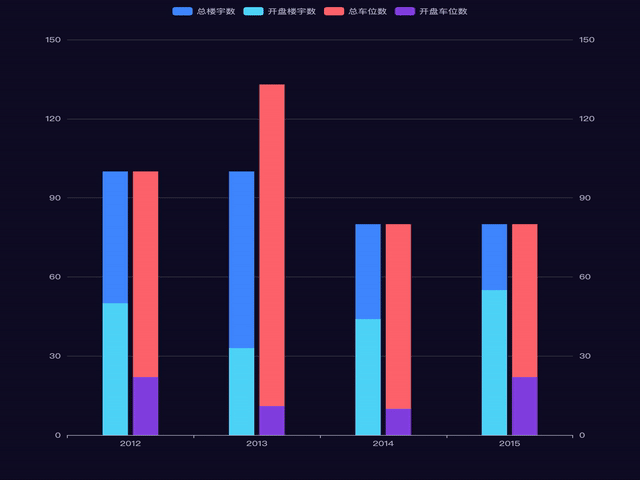
Echarts实现多柱状图重叠重叠效果
有两种重叠效果: 1. 多个柱子重叠为一个 2. 多个柱子重叠为两组 第一种,图例: 这个灰色不是阴影哦, 是柱子. 1. 使用详解 (1) series.Z 折线图组件的所有图形的 z 值。控制图形的前后顺序。 z 值小的图形会被 z 值大的图形覆盖。z 相比 zlevel 优先级更低,而且不会…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
