平面及其方程
一、曲面和交线的定义
空间解析几何中,任何曲面或曲线都看作点的几何轨迹。在这样的意义下,如果曲面SSS与三元方程:
F(x,y,z)=0(1)F(x,y,z)=0\tag{1} F(x,y,z)=0(1)
有下述关系:
- 曲面 SSS 上任一点的坐标都满足方程(1)(1)(1)
- 不在曲面SSS上的点坐标都不满足方程(1)(1)(1)
那么,方程(1)(1)(1)就叫做曲面SSS的方程,而曲面SSS就叫做方程(1)(1)(1)的图形。
上面的概念其实就是在描述数学表达式恰好能表达曲面,不多也不少。那么空间曲线又是如何定义的?
空间曲线可以看作两个曲面 S1S1S1 S2S2S2 的交线,设曲面的交线为 CCC,则交线可以应该满足方程组:
{F(x,y,z)=0G(x,y,z)=0\left\{ \begin{aligned} F(x,y,z)=0\\ G(x,y,z)=0 \end{aligned} \right. {F(x,y,z)=0G(x,y,z)=0
二、平面方程
2.1 点法式方程
确定平面中的一点及其方向就是点法式方程的基本思想。平面中的点没有什么特殊的地方,就是属于平面上的一点, 那么方向应该如何表达合适呢?答案是,平面法向量。平面法向量是一个非零向量[1]垂直与待表示的平面,由线面垂直的定义,在平面上任意向量均与该平面的法向量垂直。
因为过一点有且仅有一条与平面垂直的直线。假设我们在平面 Π\PiΠ 上有一点M0(x0,y0,z0)M_0(x_0,y_0,z_0)M0(x0,y0,z0) 和它的法向量 n⃗=(A,B,C)\vec{n}=(A,B,C)n=(A,B,C) ,这个平面被唯一确定,根据定义:
n⃗⋅M0M→=0\vec{n}\cdot\overrightarrow{M_0M}=0 n⋅M0M=0
因为n⃗=(A,B,C)\vec{n}=(A,B,C)n=(A,B,C) ,M0M→=(x−x0,y−y0,z−z0)\overrightarrow{M_0M}=(x-x_0,y-y_0,z-z_0)M0M=(x−x0,y−y0,z−z0)所以有:
A(x−x0)+B(y−y0)+C(z−z0)=0(2)A(x-x_0)+B(y-y_0)+C(z-z_0)=0\tag{2} A(x−x0)+B(y−y0)+C(z−z0)=0(2)
这就是平面任意一点(xt,yt,zt)(x_t,y_t,z_t)(xt,yt,zt) 都满足的方程,这就是平面的点法式方程,点指的是平面上一点,法指的是非零法向量。
2.2 平面的一般方程
对于一个三元一次方程表示:
Ax+By+Cz+D=0(3)Ax+By+Cz+D=0\tag{3} Ax+By+Cz+D=0(3)
任取满足该方程的一个点,代入方程:
Ax0+By0+Cz0+D=0(4)Ax_0+By_0+Cz_0+D=0\tag{4} Ax0+By0+Cz0+D=0(4)
式子(3)−(4)(3)-(4)(3)−(4):
A(x−x0)+B(y−y0)+C(z−z0)=0(5)A(x-x_0)+B(y-y_0)+C(z-z_0)=0\tag{5} A(x−x0)+B(y−y0)+C(z−z0)=0(5)
我们知道(5)(5)(5)是一个点法式方程。所以:
- 任意 x,y,zx,y,zx,y,z都属于平面
- 不属于平面上的点都不满足(5)(5)(5)
从定义上看,方程(3)(3)(3):
- 任意 x,y,zx,y,zx,y,z都属于平面
- 不属于平面上的点都不满足
这就意味着,Ax+By+Cz+D=0Ax+By+Cz+D=0Ax+By+Cz+D=0 是一个平面方程。它有以下结论:
- 一般方程的 x,y,zx,y,zx,y,z 系数其实就是一个法向量
- 如果 D=0D=0D=0 过原点
- 如果 A=0A=0A=0 法向量为 n⃗=(0,B,C)\vec{n}=(0,B,C)n=(0,B,C) ,法向量垂直 XXX 轴,对应平面平行或包含 XXX 轴
- 如果 B=0B=0B=0 法向量为 n⃗=(A,0,C)\vec{n}=(A,0,C)n=(A,0,C) ,法向量垂直 YYY 轴,对应平面平行或包含 YYY 轴
- 如果 C=0C=0C=0 法向量为 n⃗=(A,B,0)\vec{n}=(A,B,0)n=(A,B,0) ,法向量垂直 ZZZ 轴,对应平面平行或包含 ZZZ 轴
- 如果 A=B=0A=B=0A=B=0 法向量为 n⃗=(0,0,C)\vec{n}=(0,0,C)n=(0,0,C) ,法向量同时垂直 X,YX,YX,Y轴,也就是垂直于对应的XOYXOYXOY平面,对应的平面平行或者包含XOYXOYXOY
- 如果 B=C=0B=C=0B=C=0 法向量为 n⃗=(A,0,0)\vec{n}=(A,0,0)n=(A,0,0) ,法向量同时垂直 Y,ZY,ZY,Z轴,也就是垂直于对应的YOZYOZYOZ平面,对应的平面平行或者包含YOZYOZYOZ
- 如果 A=0=CA=0=CA=0=C 法向量为 n⃗=(0,B,0)\vec{n}=(0,B,0)n=(0,B,0) ,法向量同时垂直 X,ZX,ZX,Z轴,也就是垂直于对应的XOZXOZXOZ平面,对应的平面平行或者包含XOZXOZXOZ
一大串文字,其实总结一句话,看法向量坐标,如果对应分量为0,那么法向量垂直于对应分量,对应平面平行或者包含对应分量。
三、两平面的夹角
从几何上看,平面的夹角是小于或者等于90度的,但在解析几何中,我们更加倾向于用法向量之间的夹角来定义,用向量夹角表示存在一个问题,向量夹角的范围是[0,π][0,\pi][0,π],应该特别注意。
设平面 Π1\Pi_1Π1 和 Π2\Pi_2Π2 的法向量依次为 n1=(A1,B1,C1)\bold{n_1}=(A_1,B_1,C_1)n1=(A1,B1,C1) 和 n2=(A2,B2,C2)\bold{n_2}=(A_2,B_2,C_2)n2=(A2,B2,C2) ,则平面的夹角 θ\thetaθ 应为:(n1,n2^)(\widehat{\bold{n_1},\bold{n_2}})(n1,n2)或者(−n1,n2^)=π−(n1,n2^)(\widehat{\bold{-n_1},\bold{n_2}})=\pi-(\widehat{\bold{n_1},\bold{n_2}})(−n1,n2)=π−(n1,n2),选两个中的锐角或者直角,所以: cosθ=∣(n1,n2^)∣\cos\theta=|(\widehat{\bold{n_1},\bold{n_2}})|cosθ=∣(n1,n2)∣。用向量计算公式则为:
cosθ=∣A1A2+B1B2+C1C2∣A12+B12+C12A22+B22+C22(6)\cos \theta=\frac{|A_1A_2+B_1B_2+C_1C_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}}\tag{6} cosθ=A12+B12+C12A22+B22+C22∣A1A2+B1B2+C1C2∣(6)
从向量垂直和平行的充分必要条件立刻可推得:
- Π1、Π2\Pi_1、\Pi_2Π1、Π2 垂直相当于 A1A2+B1B2+C1C2=0A_1A_2+B_1B_2+C_1C_2=0A1A2+B1B2+C1C2=0
- Π1、Π2\Pi_1、\Pi_2Π1、Π2 平行或重合相当于 A1A2+B1B2+C1C2=0\frac{A_1}{A_2}+\frac{B_1}{B_2}+\frac{C_1}{C_2}=0A2A1+B2B1+C2C1=0
[1] 主要是你是零向量也没啥意思,什么信息都给不了
相关文章:

平面及其方程
一、曲面和交线的定义 空间解析几何中,任何曲面或曲线都看作点的几何轨迹。在这样的意义下,如果曲面SSS与三元方程: F(x,y,z)0(1)F(x,y,z)0\tag{1} F(x,y,z)0(1) 有下述关系: 曲面 SSS 上任一点的坐标都满足方程(1)(1)(1)不在曲…...

7 配置的封装
概述 IPC设备通常有三种配置信息:一是默认配置,存储了设备所有配置项的默认值,默认配置是只读的,不能修改;二是用户配置,存储了用户修改过的所有配置项;三是私有配置,存储了程序内部使用的一些配置项,比如:固件升级的URL、固件升级标志位等。恢复出厂设置的操作,实际…...

03_Docker 入门
03_Docker 入门 文章目录03_Docker 入门3.1 确保 Docker 已经就绪3.2 运行我们的第一个容器3.3 使用第一个容器3.4 容器命名3.5 重新启动已经停止的容器3.6 附着到容器上3.7 创建守护式容器3.8 容器内部都在干些什么3.9 Docker 日志驱动3.10 查看容器内的进程3.11 Docker 统计信…...

Python 为什么要 if __name__ == “__main__“:
各位读者,你们知道以下两个Python文件有什么区别吗? main1.py def main():output Helloprint(output)if __name__ "__main__":main()main2.py output Hello print(output)当我们直接运行 main1.py 与 main2.py 的时候,程序都…...
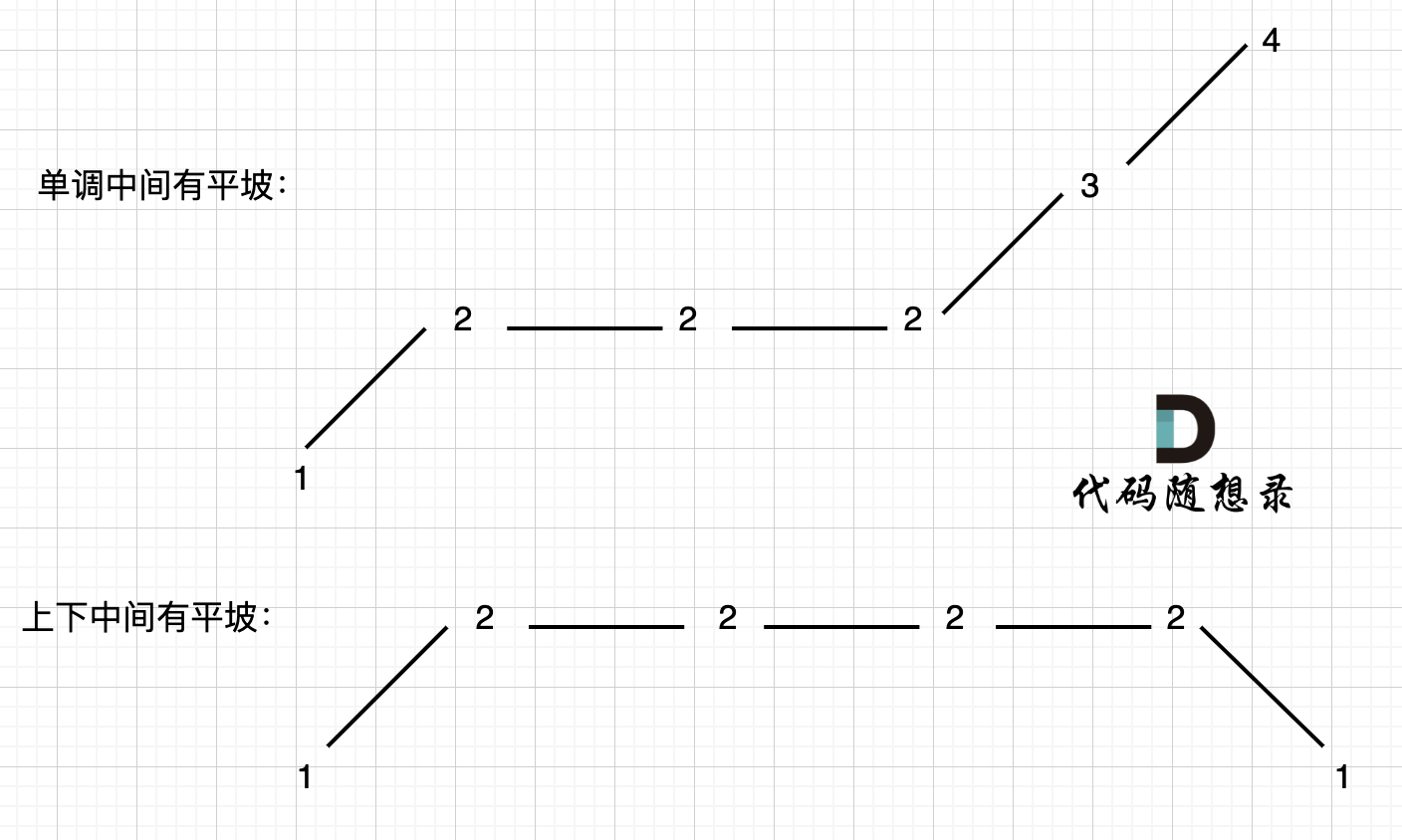
455. 分发饼干、376. 摆动序列、53. 最大子数组和
455.分发饼干 题目描述: 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块…...
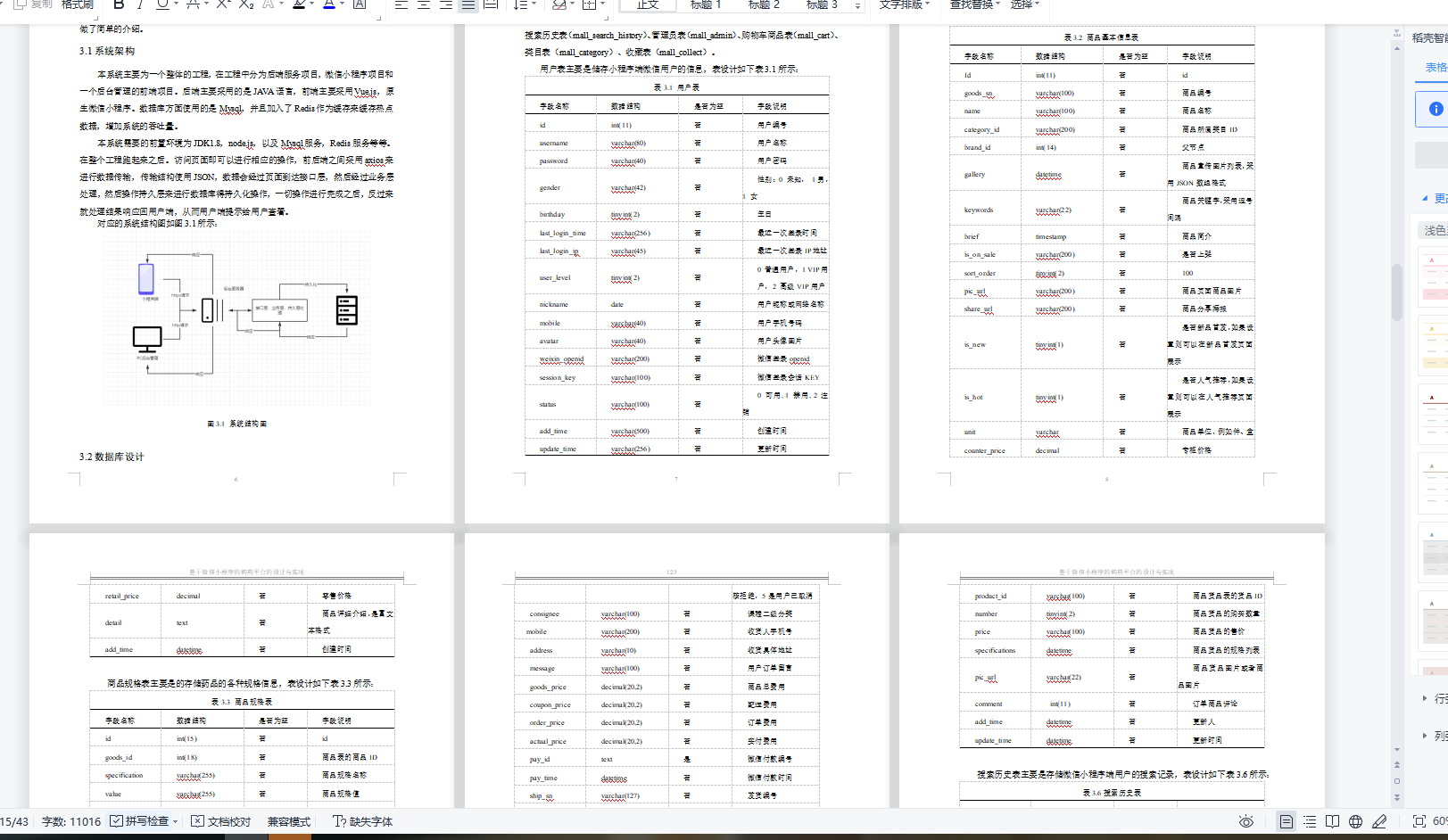
基于Springbot+微信小程序的购药平台的设计与实现
基于Springbot微信小程序的购药平台的设计与实现 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、…...

aws lambda rust的sdk和自定义运行时
rust的aws sdk 参考资料 https://docs.aws.amazon.com/sdk-for-rust/latest/dg/getting-started.htmlhttps://awslabs.github.io/aws-sdk-rust/https://github.com/awslabs/aws-sdk-rusthttps://github.com/awsdocs/aws-doc-sdk-examples/tree/main/rust_dev_preview rus sd…...
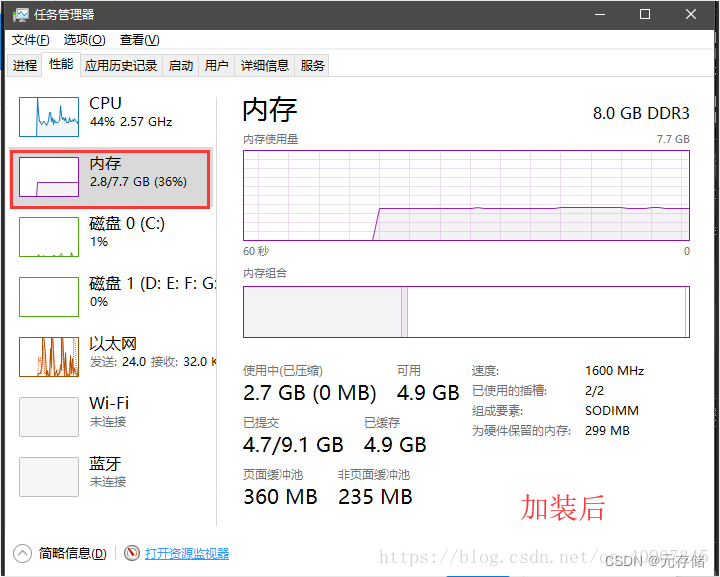
[安装之3] 笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

极客时间左耳听风-高效学习
左耳听风——高效学习篇 P95 | 高效学习:端正学习态度 本人真实⬇️⬇️⬇️⬇️ “ 大部分人都认为自己爱学习,但是: 他们都是只有意识没有行动,他们是动力不足的人。 他们都不知道自己该学什么,他们缺乏方向和目标。…...

MSR寄存器访问
1.介绍 MSR是CPU的一组64位寄存器,每个MSR都有它的地址值(如下图所示),可以分别通过RDMSR 和WRMSR 两条指令进行读和写的操作。 如图中为8个P-state寄存器,地址分别为0xC001 0064 ~ 0xC001 006B,每个寄存…...
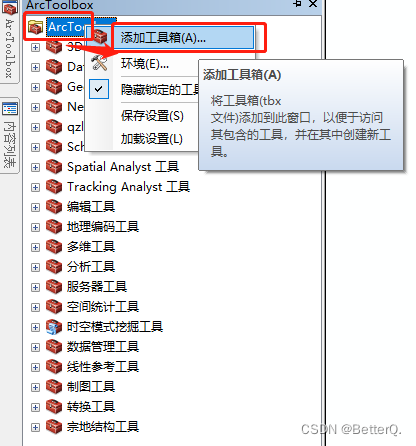
ArcGIS:模型构建器实现批量按掩膜提取影像
用研究区域的矢量数据来裁剪栅格数据集时,一般我们使用ArcGIS中的【按掩膜提取工具】。如果需要裁剪的栅格数据太多,处理起来非常的麻烦,虽然ArcGIS中有批处理的功能,但是还是需要手动选择输入输出数据。 如下图,鼠标…...

算法刷题打卡第94天: 找出给定方程的正整数解
找出给定方程的正整数解 难度:中等 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调…...
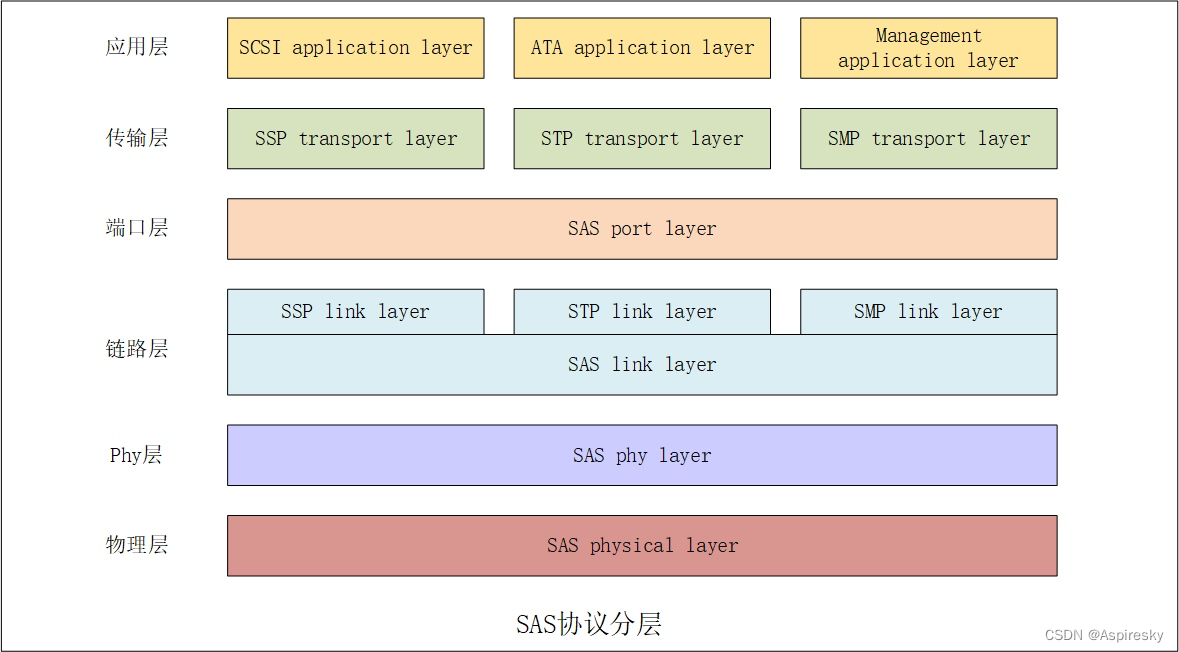
浅析SAS协议(1):基本介绍
文章目录概述SAS协议发展历程SAS技术特性SAS设备拓扑SAS phySAS地址SAS设备类型SAS协议分层参考链接概述 SAS,全称Serial Attached SCSI,即串行连结SCSI,是一种采用了串行总线的高速互连技术。通过物理上使用串行总线连结,在链路…...
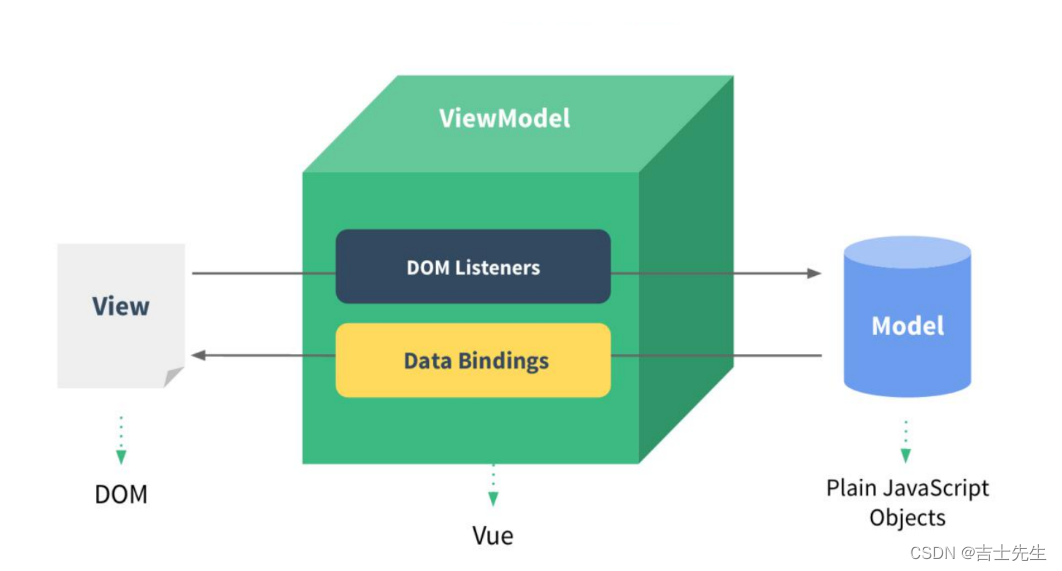
93.【Vue-细刷-02】
Vue-02(十六)、基本列表渲染 (v-for)1.使用v-for遍历数组2.使用v-for遍历对象3.使用v-for遍历字符串(十七)、列表过滤 (filter())1.⭐JS中Change属性的原生状态⭐2.使用watch监听实现3.const {xxx} this 在Vue的作用⭐⭐4.JS箭头函数参数的简写⭐5.使用computed进行计算实现(最…...
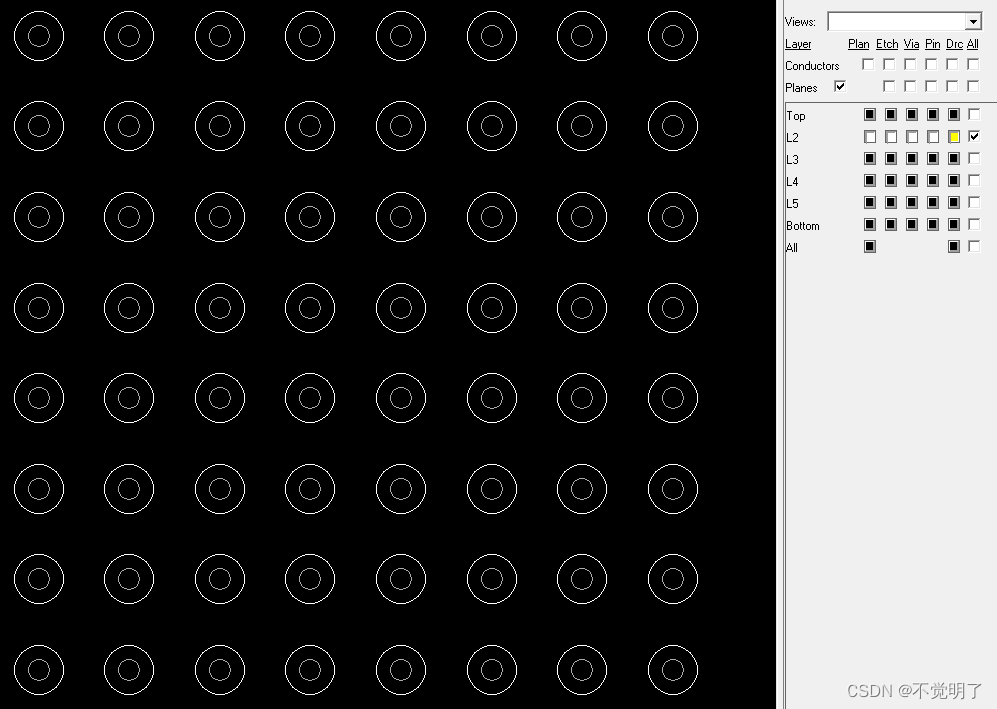
Allegro负片层不显示反盘的原因和解决办法
Allegro负片层不显示反盘的原因和解决办法 在用Allegro做PCB设计的时候,负片设计是较为常用的一种方式,有时会出现打开负片层却看不到反盘的情况,如下图 L2层是负片层 L2层仍然只能看到盘 如何才能看到反盘显示的效果,具体操作如下 首先确定L2层层叠里面设置的是负片...
ACM数论 裴蜀定理(贝祖定理)
一.内容定义 「裴蜀定理」,又称贝祖定理(Bzouts lemma)。是一个关于最大公约数的定理。其内容定义为:对于不全为零的任意整数 a 和 b,记二者的最大公约数为 g 即 gcd(a,b) g,则对于任意整数 x 和 y 都一定…...
解析)
基础篇—CSS Position(定位)解析
CSS Position(定位) position 属性指定了元素的定位类型。 position 属性的五个值: relativefixedabsolutesticky元素可以使用的顶部,底部,左侧和右侧属性定位。然而,这些属性无法工作,除非是先设定position属性。他们也有不同的工作方式,这取决于定位方法。 1、static…...

正则表达式与grep
基本正则表达式BRE集合 匹配字符匹配次数位置锚定 符号作用^尖角号,用于模式的最正常,如“^haha”,匹配以haha单词开头的行$美元符,用于模式的最右侧,如“haha$”,表示haha单词结尾的行^$组合符ÿ…...
开发必备的IDEA 插件!效率提升 50 倍!
日常开发中,面向百度编程的程序员,很多时候,你跟大佬级别的差距,可能不仅仅是知识面的差距,还有就是开发效率的差距。以下是我常用的几个IDEA插件,废话不多说,直接肝干货! 1. Codot…...

aws eks 集群访问ecr仓库拉取镜像的认证逻辑
本文主要讨论三个问题 ecr帮助程序在docker上如何配置eks集群访问ecr仓库的逻辑kubelet授权ecr的源码分析 ecr帮助程序 在docker环境下,可以通过在$HOME/.docker/config.json中指定凭证管理程序 docker login aws同样提供了证书助手,避免手动执行ecr认…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
