电源控制--对数与db分贝

在控制理论中,"db"通常表示分贝(decibel)的缩写。分贝是一种用于度量信号强度、增益或衰减的单位。
在控制系统中,分贝常用于描述信号的增益或衰减。通常,增益以正数的分贝值表示,而衰减以负数的分贝值表示。
在控制系统中,分贝常用于以下方面:
-
增益表示:分贝可以用于表示信号的增益。例如,一个系统的增益为20 dB表示信号的输出是输入的10倍。
-
衰减表示:分贝可以用于表示信号的衰减。例如,一个系统的衰减为-40 dB表示信号的输出是输入的1/100倍。
-
系统性能指标:在控制系统的频率响应分析中,分贝常用于表示系统的增益或衰减随频率变化的情况。频率响应曲线通常以分贝为单位进行绘制,以显示系统在不同频率下的增益或衰减特性。
总而言之,"db"在控制理论中通常表示分贝,用于表示信号的增益、衰减或频率响应特性。
对数是数学中的一种常见运算,具有以下基本且常用的法则:
-
对数乘法法则:
logₐ (xy) = logₐ x + logₐ y
对数乘法法则表明,对数的底数相同的两个数相乘的对数等于这两个数分别取对数后的和。 -
对数除法法则:
logₐ (x/y) = logₐ x - logₐ y
对数除法法则表明,对数的底数相同的两个数相除的对数等于这两个数分别取对数后的差。 -
对数幂法则:
logₐ (x^r) = r * logₐ x
对数幂法则表明,对数的底数相同的一个数的幂的对数等于该数的对数与幂的乘积。 -
换底公式:
log_b x = log_a x / log_a b
换底公式允许我们将一个对数的底数转换为另一个对数的底数,通过将对数的底数转换为常用的对数底数(如自然对数的底数e或常用对数的底数10)来计算。
这些基本的对数运算法则在解决数学问题、进行数值计算和进行函数分析等方面经常被使用。它们帮助简化对数的计算过程,并提供了对数之间的关系和性质的理解。
相关文章:

电源控制--对数与db分贝
在控制理论中,"db"通常表示分贝(decibel)的缩写。分贝是一种用于度量信号强度、增益或衰减的单位。 在控制系统中,分贝常用于描述信号的增益或衰减。通常,增益以正数的分贝值表示,而衰减以负数的…...
)
LeetCode 1749. 任意子数组和的绝对值的最大值(前缀和)
题目: 链接:LeetCode 1749. 任意子数组和的绝对值的最大值 难度:中等 给你一个整数数组 nums 。一个子数组 [numsl, numsl1, …, numsr-1, numsr] 的 和的绝对值 为 abs(numsl numsl1 … numsr-1 numsr) 。 请你找出 nums 中 和的绝对…...
python爬虫相关
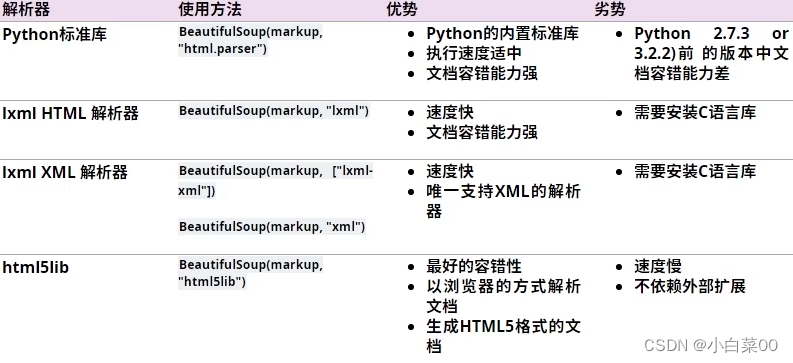
目录 初识爬虫 爬虫分类 网络爬虫原理 爬虫基本工作流程 搜索引擎获取新网站的url robots.txt HTHP协议 Resquests模块 前言: 安装 普通请求 会话请求 response的常用方法 简单案例 aiohttp模块 使用前安装模块 具体案例 数据解析 re解析 bs4…...
PAT(Advanced Level) Practice(with python)——1023 Have Fun with Numbers
Code N int(input()) D_N 2*N # print(Yes)if len(str(D_N))>len(str(N)):print(No) else:for s in str(D_N):if s not in str(N) or str(D_N).count(s)!str(N).count(s):print("No")breakelse:print(Yes) print(D_N)...

springboot vue 初步集成onlyoffice
文章目录 前言一、vue ts1. 安装依赖2. onlyoffice组件实现(待优化)3. 使用组件4. 我的配置文件 二、springboot 回调代码1. 本地存储 三、效果展示踩坑总结问题1问题2 前言 对接onlyoffice,实现文档的预览和在线编辑功能。 一、vue ts …...
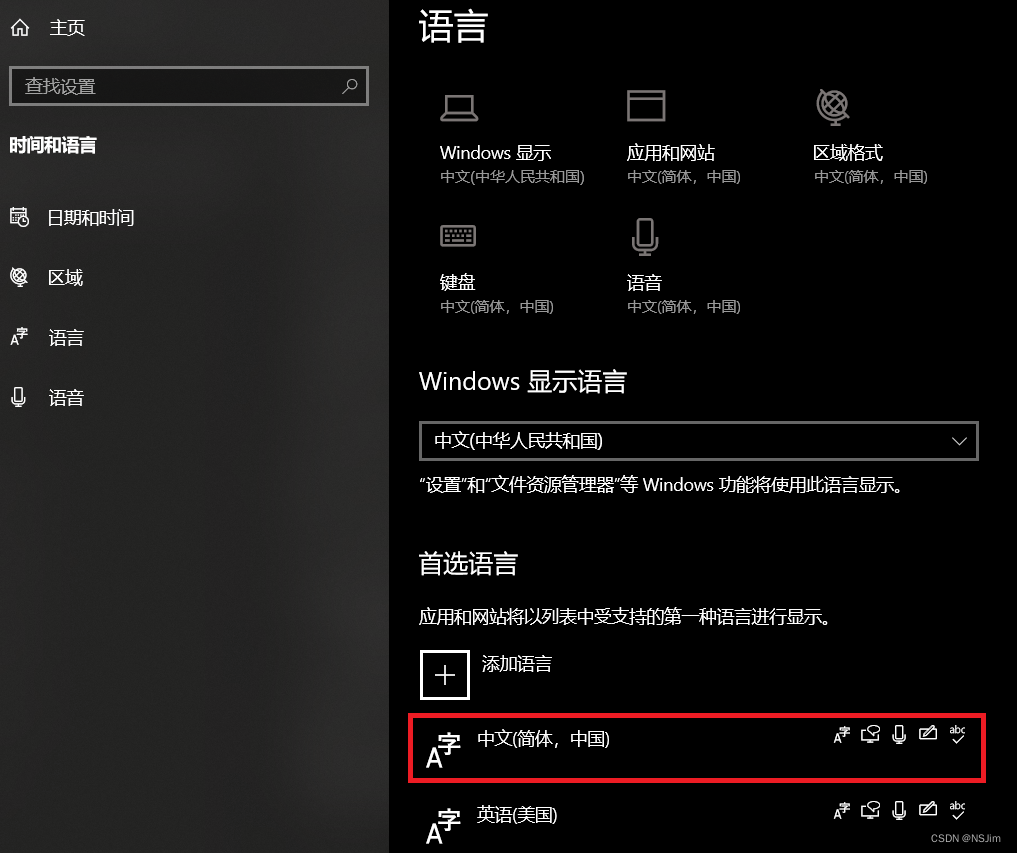
Win10语言设置 - 显示语言和应用语言
前言 Win10的语言设置可以设置显示语言和应用语言。其中,显示语言用于显示系统文字;应用语言用于应用程序显示文字。下文介绍如何设置。 显示语言 打开系统设置,选择时间和语言,如下图: 修改Windows显示语言即可更…...

RxJava的前世【RxJava系列之设计模式】
一. 前言 学习RxJava,少不了介绍它的设计模式。但我看大部分文章,都是先将其用法介绍一通,然后再结合其用法,讲解其设计模式。这样当然有很多好处,但我个人觉得,这种介绍方式,对于没有接触过Rx…...

sql 语句 字段字符串操作
substring_index() 函数 字符串截取 表达式:substring_index(column,str,count) 释义:截取字符串column,str出现从前往后数第count次,之前的所有字符 示例语句:SELECT substring_index(‘www.baidu.com’,‘.’,2) 结…...
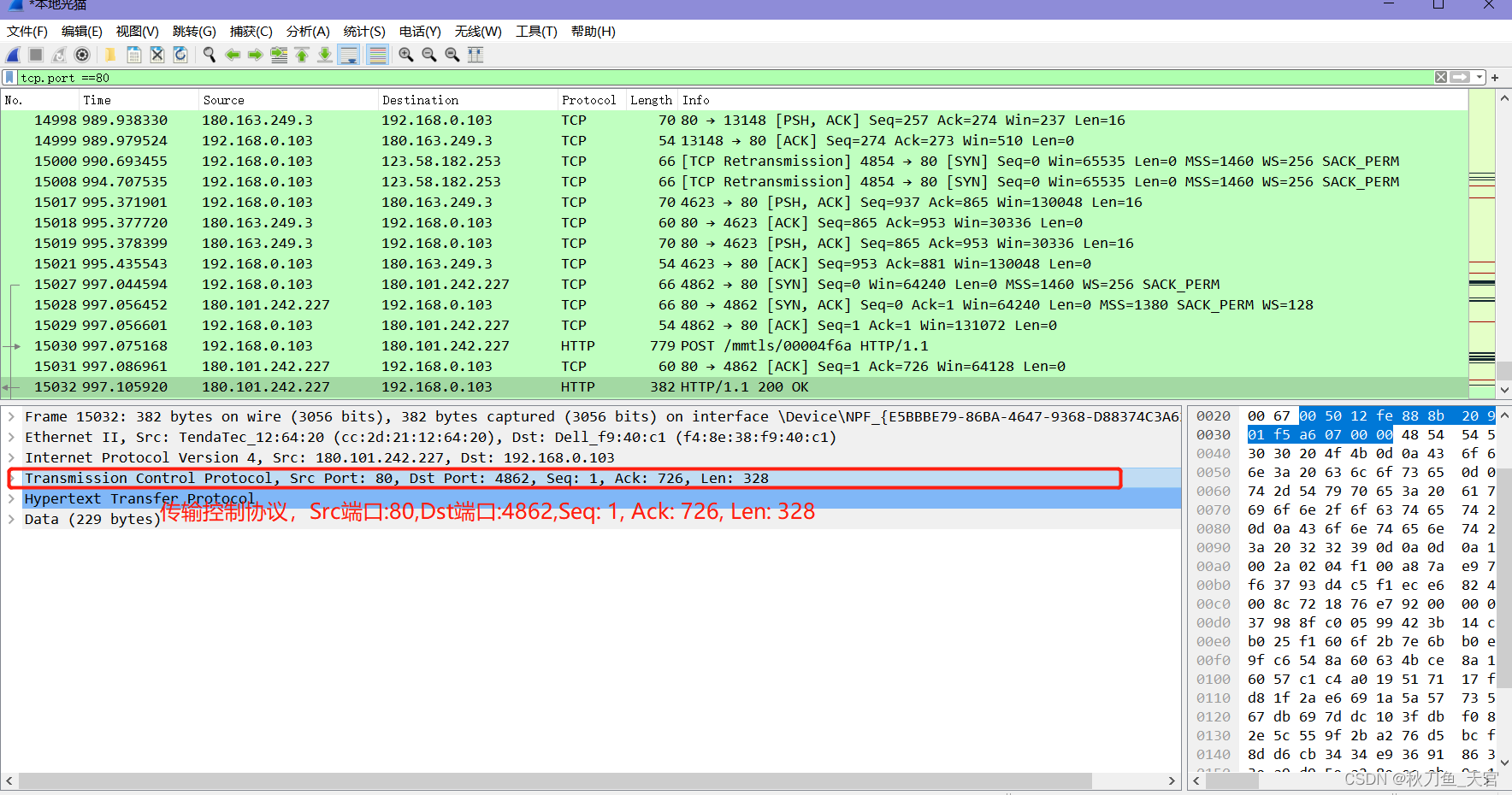
【网络工程】网络流量分析工具 Wireshark
文章目录 第一章:WireShark介绍第二章:WireShark应用第三章:Wireshark 实战 第一章:WireShark介绍 Wireshark (前身 Ethereal):它是一个强大的网络封包分析软件工具 ! 此工具使用WinPCAP作为接口,直接与网卡…...
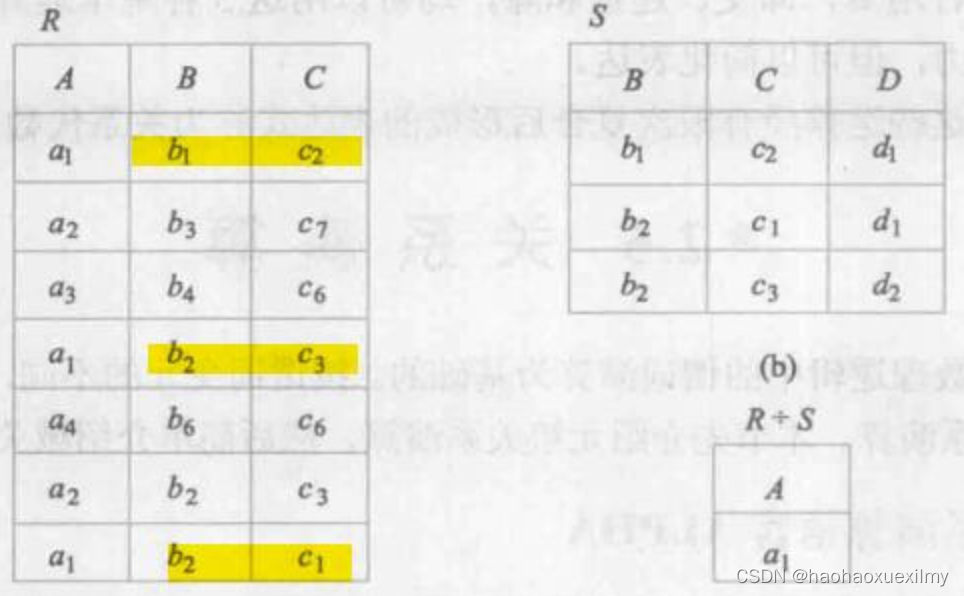
数据库总结
第一章绪论 一、数据库系统概述 1. 数据库的4个基本概念 1.数据:数据库中存储的基本对象,描述事物的符号记录。 2.数据库:长期储存在计算机内、有组织的、可共享的大量数据的集合。较小的冗余度、较高的数据独立性、易扩展性 3.数据库管…...

虹科方案 | 成都大运会进行时,保障大型活动无线电安全需要…
成都大运会 7月28日,备受关注的第31届世界大学生夏季运动会在成都正式开幕。据悉,这是全球首个5G加持的智慧大运会,也是众多成熟信息技术的综合“应用场”。使用基于5G三千兆、云网、8K超高清视频等技术,在比赛现场搭建多路8K摄像…...
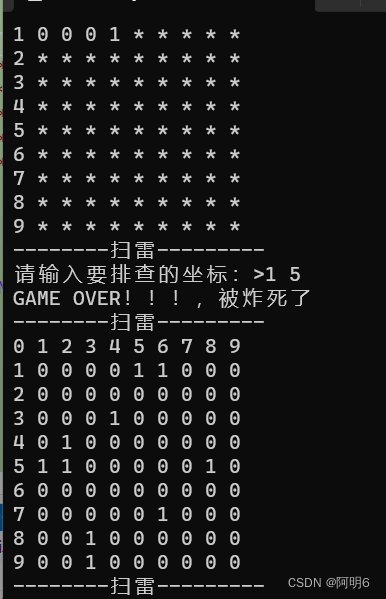
【C语言】扫雷 小游戏
文章目录 一、游戏规则二、 代码逻辑三、游戏实现1. 游戏菜单设计2.设计雷区并随机布置雷(1) 设置雷区(2) 布置雷 3.排查雷 四、源码 一、游戏规则 1. 在9*9的小格子中,任意选取一个坐标(格子),选择后发现,如果没点中雷…...

Jmeter(六) - 从入门到精通 - 建立数据库测试计划(详解教程)
1.简介 在实际工作中,我们经常会听到数据库的性能和稳定性等等,这些有时候也需要测试工程师去评估和测试,因此这篇文章主要介绍了jmeter连接和创建数据库测试计划的过程,在文中通过示例和代码非常详细地介绍给大家,希望对各位小伙…...
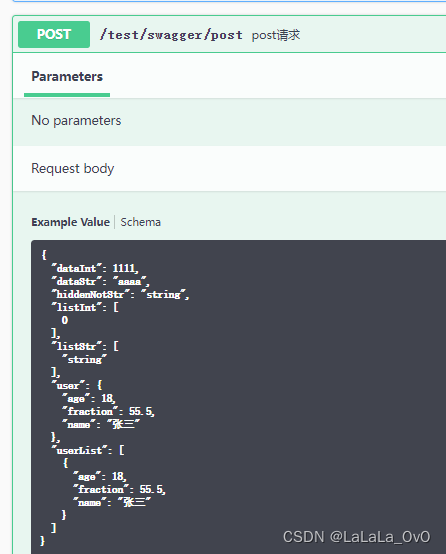
swagger 3.0 学习笔记
引入pom <dependency><groupId>io.springfox</groupId><artifactId>springfox-boot-starter</artifactId><version>3.0.0</version></dependency>配置 import io.swagger.models.auth.In; import io.swagger.v3.oas.annotati…...

07 |「异步任务」
前言 实践是最好的学习方式,技术也如此。 文章目录 前言一、进程与线程1、进程2、线程 二、实现 一、进程与线程 1、进程 进程(Process)是操作系统分配资源的基本单位,它是一个执行中的程序实例;每个进程都有自己独立的内存空间,不同进程的内存是相互独…...

LoRaWan网关设计之入门指南
快速开始 以下是在目标平台本身上构建和运行 LoRaWan网关 的三步快速入门指南。 第 1 步:克隆 网关源码库 git clone https://github.com/lorabasics/basicstation.git...
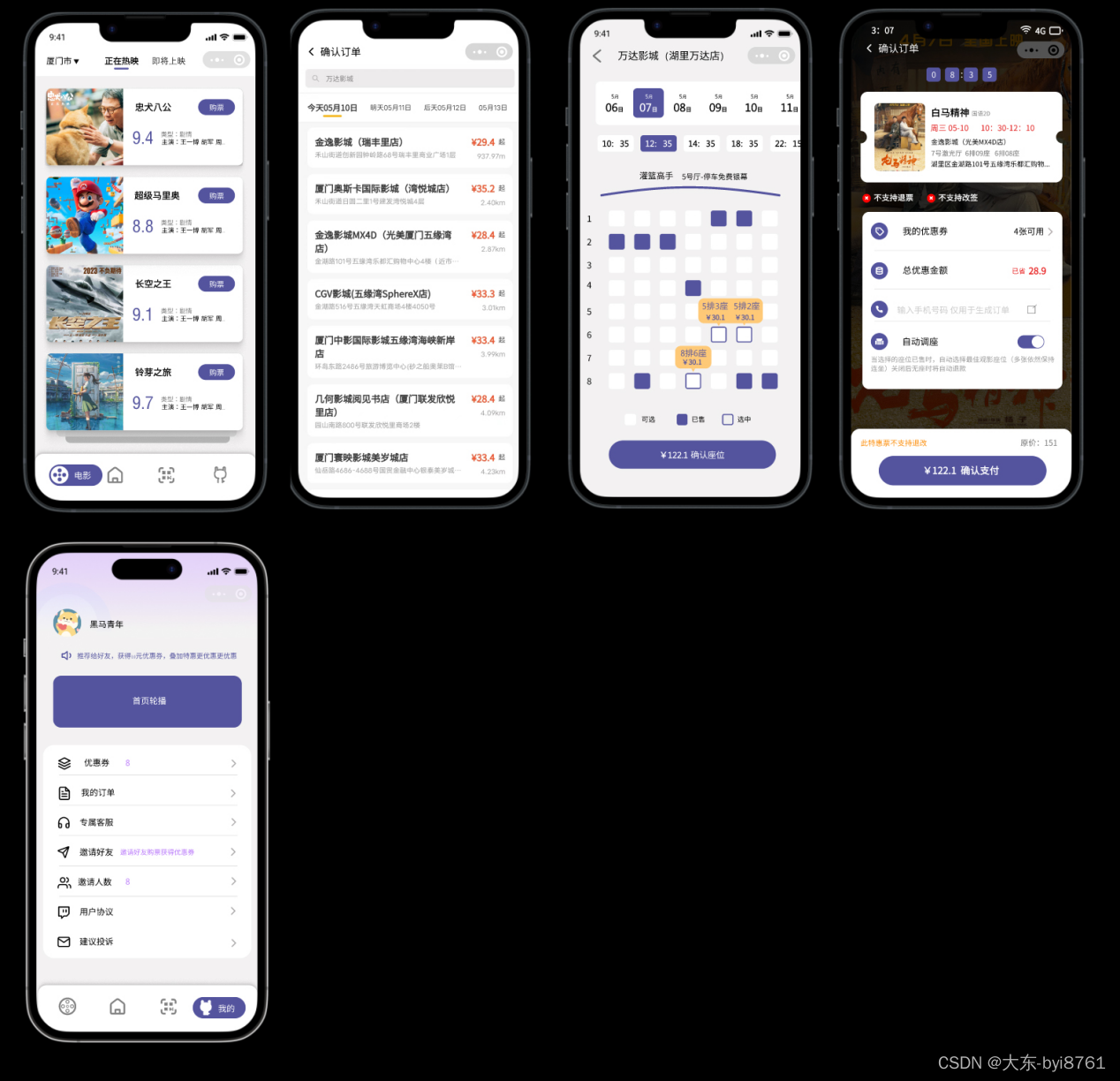
互联网电影购票选座后台管理系统源码开发
搭建一个互联网电影购票选座后台管理系统需要进行以下步骤: 1. 需求分析:首先要明确系统的功能和需求,包括电影列表管理、场次管理、座位管理、订单管理等。 2. 技术选型:选择适合的技术栈进行开发,包括后端开发语言…...

[ K8S ] yaml文件讲解
目录 查看 api 资源版本标签写一个yaml文件demo创建资源对象查看创建的pod资源创建service服务对外提供访问并测试//创建资源对象查看创建的service写yaml太累怎么办? Kubernetes 支持 YAML 和 JSON 格式管理资源对象 JSON 格式:主要用于 api 接口之间消…...
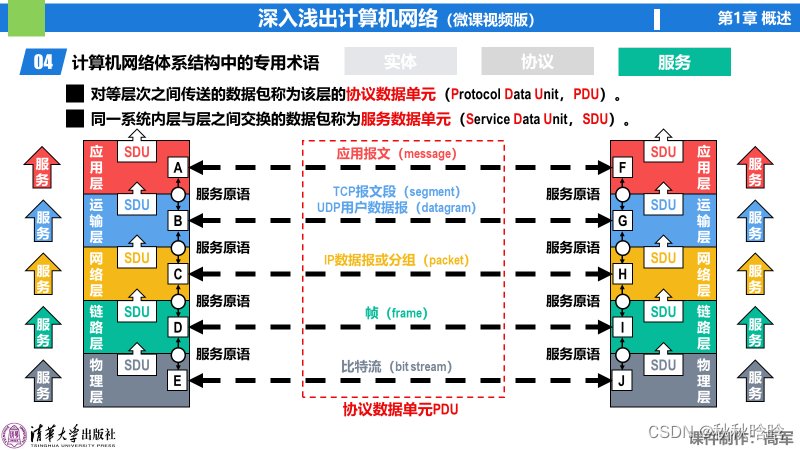
【《深入浅出计算机网络》学习笔记】第1章 概述
内容来自b站湖科大教书匠《深入浅出计算机网络》视频和《深入浅出计算机网络》书籍 目录 1.1 信息时代的计算机网络 1.1.1 计算机网络的各类应用 1.1.2 计算机网络带来的负面问题 1.2 因特网概述 1.2.1 网络、互联网与因特网的区别与关系 1.2.1.1 网络 1.2.1.2 互联网 …...
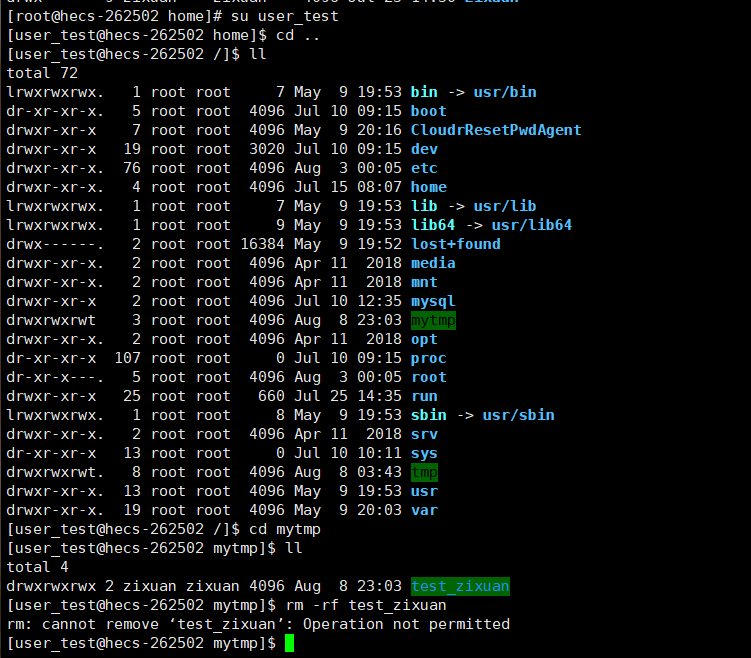
二、Linux中权限、shell命令及运行原理
shell命令及运行原理 我们使用Linux时,并不是直接访问操作系统,为什么不是直接访问操作系统呢? 如果用户直接访问操作系统,不仅使用难度大,而且不安全,容易把系统文件损坏。 那么我们通常是如何访问操作系统…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
