Segment Anything(SAM) 计算过程
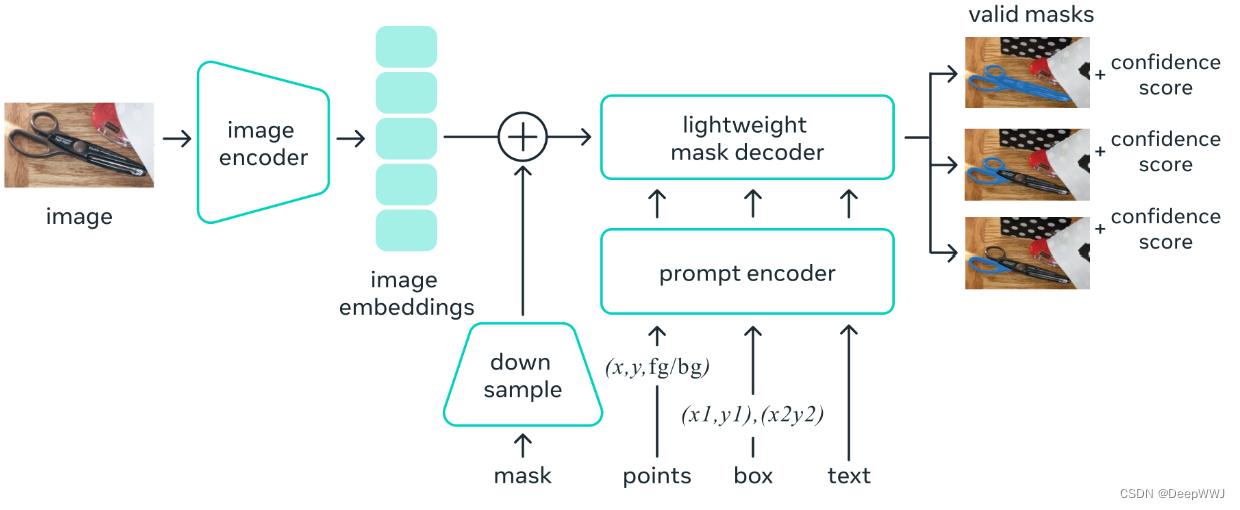
- 给定输入图像 I ∈ R 3 × H × W I \in R^{3 \times H \times W} I∈R3×H×W。
- 给定需要的prompts:
- M ∈ R 1 × H × W M \in R^{1 \times H \times W} M∈R1×H×W,代表图片的前背景信息。
- P ∈ R N × 2 P \in R^{N \times 2} P∈RN×2,其中 N N N 是点的个数,2 代表坐标。
- B ∈ R 4 B \in R^{4} B∈R4,4 代表左上角与右下角点的坐标。
- T T T 代表一段文本,暂时还未开放。
- I I I 输入到image encoder中提取特征,得到image embeddings: f I = V I T ( I ) , f I ∈ R c × h × w f^{I}=VIT(I),f^{I} \in R^{c \times h \times w} fI=VIT(I),fI∈Rc×h×w c , h , w c,h,w c,h,w 分别是特征维度与特征的空间高,宽。
- 得到稠密编码 f D ∈ R c × h × w f^{D} \in R^{c \times h \times w} fD∈Rc×h×w。如果有 M M M,将其输入到卷积网络中卷它,如果没有的话,直接复制no_mask_embed向量填充。
- 得到稀疏编码 f S ∈ R K × c f^{S} \in R^{K \times c} fS∈RK×c。
- 对于点 P P P,进行位置编码,得到 f P ∈ R N × c f^P \in R^{N \times c} fP∈RN×c (每个点映射为一个 c c c 维向量),并且 f P f^P fP 中不同区域(填充部分,前景,背景)要添加对应的编码加以区分。
- 对于框 B B B,首先重塑为两个点,然后使用与点相同的方式进行点编码,最后两个点加上对应的坐上角与右下角的编码,最终得到 f B ∈ R 2 × c f^B \in R^{2 \times c} fB∈R2×c。
- 最后将 f P f^P fP 与 f B f^B fB 拼接起来作为稀疏编码,最后的稀疏编码可能只包含点编码或框编码,但实质都是点编码,只是框编码会额外加两个可学习编码加以区分,即三种情况: K = N ∣ K = 2 ∣ K = N + 2 K =N|K=2|K=N+2 K=N∣K=2∣K=N+2
- f k e y = f I + f D , f k e y ∈ R c × h × w f^{key}=f^{I}+f^{D},f^{key} \in R^{c \times h \times w} fkey=fI+fD,fkey∈Rc×h×w 作为mask decoder的 key
- 加入各种token输入到mask decoder中,作为 query。iou_token: f i o u ∈ R 1 × c f^{iou} \in R^{1 \times c} fiou∈R1×c,mask_tokens: f m a s k ∈ R 4 × c f^{mask} \in R^{4 \times c} fmask∈R4×c (3个mask+1个背景)。 f q u e r y = C a t ( f i o u , f m a s k , f S ) , f q u e r y ∈ R ( 5 + K ) × c f^{query}=Cat(f^{iou},f^{mask},f^S),f^{query} \in R^{(5 + K) \times c} fquery=Cat(fiou,fmask,fS),fquery∈R(5+K)×c f k e y , f q u e r y = M a s k D e c o d e r ( f k e y , f q u e r y , f p e ) f^{key},f^{query}=MaskDecoder(f^{key},f^{query},f^{pe}) fkey,fquery=MaskDecoder(fkey,fquery,fpe) f p e f^{pe} fpe是位置编码
- 最终得到 f k e y ∈ R c × h × w f^{key} \in R^{c \times h \times w} fkey∈Rc×h×w, f q u e r y ∈ R ( 5 + K ) × c f^{query} \in R^{(5 + K) \times c} fquery∈R(5+K)×c。
- 随后 f k e y f^{key} fkey 进行反卷积,还原到图像尺寸 H H H, W W W(实际会进行一些采样)。
- f q u e r y f^{query} fquery 的第一个表示iou,后三个表示mask,对后三个进行线性映射。
- 前两步结果求向量积,得到mask预测。 f i o u = f q u e r y [ : , 0 , : ] f^{iou}=f^{query}[:,0,:] fiou=fquery[:,0,:] f m a s k = f q u e r y [ : , 1 : 4 , : ] f^{mask}=f^{query}[:,1:4,:] fmask=fquery[:,1:4,:] f m a s k = M L P ( f m a s k ) , f m a s k ∈ R 3 × c f^{mask}=MLP(f^{mask}),f^{mask} \in R^{3 \times c} fmask=MLP(fmask),fmask∈R3×c f m a s k = M a t M u l ( f m a s k , f k e y ) , f m a s k ∈ R 3 × H × W f^{mask}=MatMul(f^{mask}, f^{key}),f^{mask} \in R^{3 \times H \times W} fmask=MatMul(fmask,fkey),fmask∈R3×H×W f i o u = M L P ( f i o u ) , f i o u ∈ R 3 f^{iou}=MLP(f^{iou}),f^{iou} \in R^{3} fiou=MLP(fiou),fiou∈R3
- 最终模型得到 3 个 mask 以及 3 个置信度。
相关文章:

Segment Anything(SAM) 计算过程
给定输入图像 I ∈ R 3 H W I \in R^{3 \times H \times W} I∈R3HW。给定需要的prompts: M ∈ R 1 H W M \in R^{1 \times H \times W} M∈R1HW,代表图片的前背景信息。 P ∈ R N 2 P \in R^{N \times 2} P∈RN2,其中 N N N 是点的个数…...

Nacos配置文件读取源码解析
Nacos配置文件读取 本篇文章是探究,springboot启动时nacos是如何将配置中心的配置读取到springboot环境中的 PropertySourceLocator org.springframework.cloud.bootstrap.config.PropertySourceLocator 是 springcloud 定义的一个顶级接口,用来定义所…...

Linux0.11内核源码解析-fcntl.c/iotcl.c/stat.c
fcntl fcntl.c实现了文件控制系统调用fcntl和两个文件句柄描述符的复制系统调用dup()和dup2()。 dup返回当前值最小的未用句柄,dup2返回指定新句柄的数值,句柄的复制操作主要用在文件的标准输入、输出重定向和管道方面。 dupfd 复制文件句柄ÿ…...

OpenStack简介
OpenStack简介 目录 OpenStack简介 1、云计算模式2、云计算 虚拟化 openstack之间的关系?3、OpenStack 中有哪些组件?4、计算节点负责虚拟机运行5、网络节点负责对外网络与内网之间的通信 5.1 网络节点仅包含Neutron服务5.2 网络节点包含三个网络端口6、…...
二分法的应用
文章目录 什么是二分法🎮二分查找的优先级二分查找的步骤💥图解演示🧩 代码演示🫕python程序实现🐈⬛C程序实现🐕🦺C程序实现🐯Java程序实现🐳 非常规类二分查找&…...

ChatGPT在大规模数据处理和信息管理中的应用如何?
ChatGPT作为一种强大的自然语言处理模型,在大规模数据处理和信息管理领域有着广泛的应用潜力。它可以利用其文本生成、文本理解和问答等能力,为数据分析、信息提取、知识管理等任务提供智能化的解决方案。以下将详细介绍ChatGPT在大规模数据处理和信息管…...
【算法篇C++实现】五大常规算法
文章目录 🚀一、分治法⛳(一)算法思想⛳(二)相关代码 🚀二、动态规划算法⛳(一)算法思想⛳(二)相关代码 🚀三、回溯算法⛳(一…...

MySQL和钉钉单据接口对接
MySQL和钉钉单据接口对接 数据源系统:钉钉 钉钉(DingTalk)是阿里巴巴集团打造的企业级智能移动办公平台,是数字经济时代的企业组织协同办公和应用开发平台。钉钉将IM即时沟通、钉钉文档、钉闪会、钉盘、Teambition、OA审批、智能人事、钉工牌…...

layui的基本使用-日期控件的业务场景使用入门实战案例一
效果镇楼; 1 前端UI层面; <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport&…...
【2.1】Java微服务:详解Hystrix
✅作者简介:大家好,我是 Meteors., 向往着更加简洁高效的代码写法与编程方式,持续分享Java技术内容。 🍎个人主页:Meteors.的博客 💞当前专栏: Java微服务 ✨特色专栏: 知识分享 &am…...
Apache2.4源码安装与配置
环境准备 openssl-devel pcre-devel expat-devel libtool gcc libxml2-devel 这些包要提前安装,否则httpd编译安装时候会报错 下载源码、解压缩、软连接 1、wget下载[rootnode01 ~]# wget https://downloads.apache.org/httpd/httpd-2.4.57.tar.gz --2023-07-20 …...
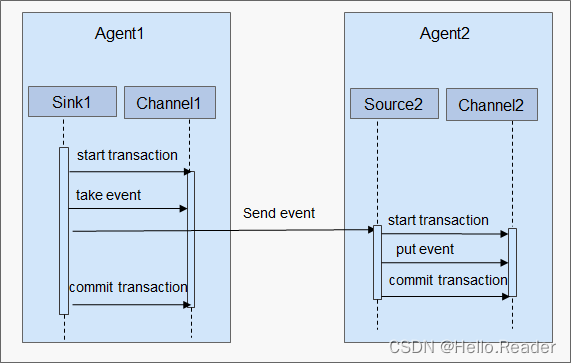
Flume原理剖析
一、介绍 Flume是一个高可用、高可靠,分布式的海量日志采集、聚合和传输的系统。Flume支持在日志系统中定制各类数据发送方,用于收集数据;同时,Flume提供对数据进行简单处理,并写到各种数据接受方(可定制&…...
)
【leetcode】202. 快乐数(easy)
编写一个算法来判断一个数 n 是不是快乐数。 「快乐数」 定义为: 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果这个过程 结果为 1,…...
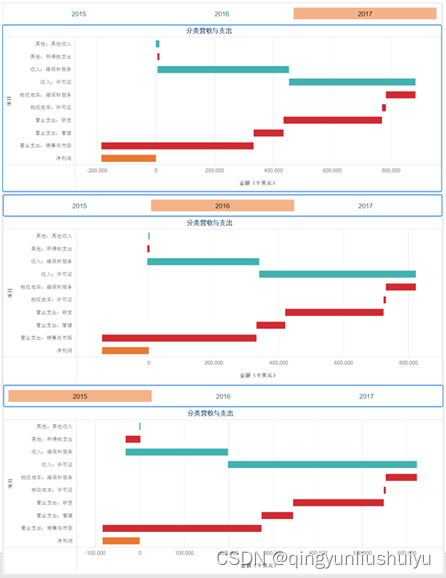
如何用瀑布图分析公司年报
原创: MicroStrategy微策略中国 , Jiping Sun 微策略企业级数据分析与移动应用9月21日2018年 摘要:利用达析报告开箱即用的瀑布图来展示各个度量值如何增加或减少。下载MicroStrategy Desktop 10.11以上版本,自己动手创建瀑布图。 瀑布图是由…...
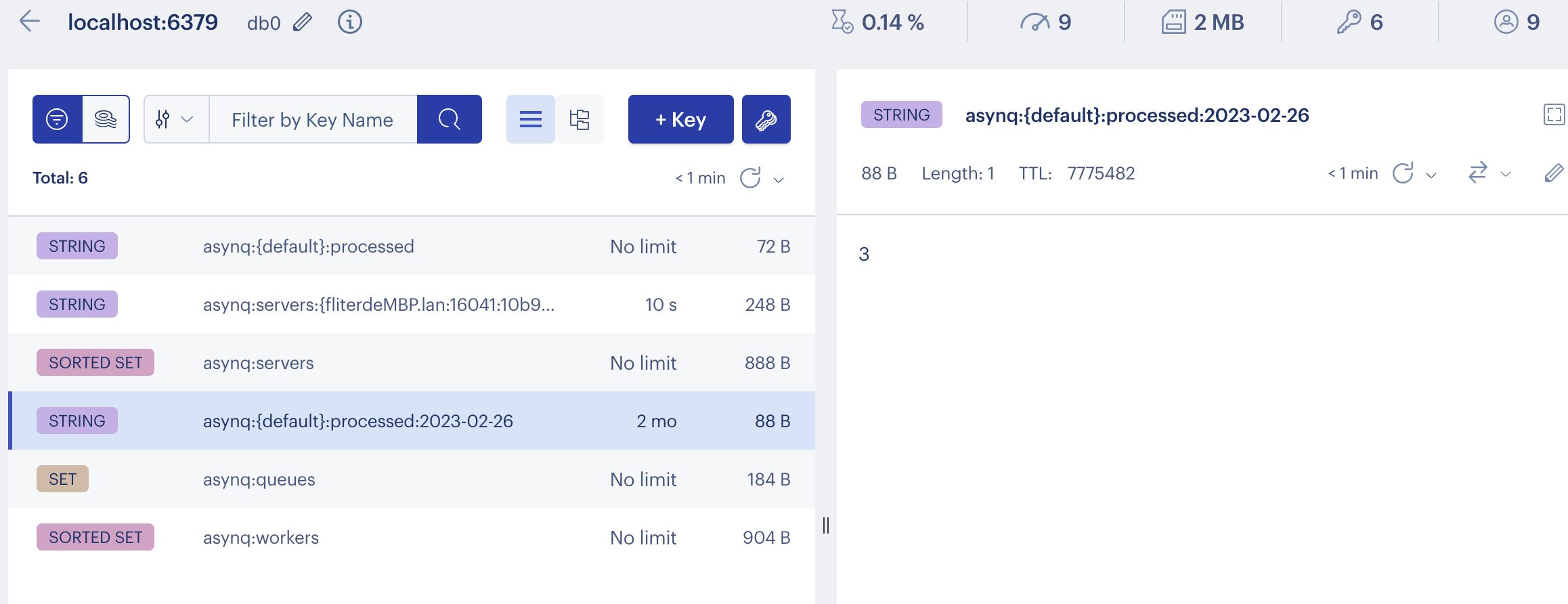
Asynq: 基于Redis实现的Go生态分布式任务队列和异步处理库
Asynq[1]是一个Go实现的分布式任务队列和异步处理库,基于redis,类似Ruby的sidekiq[2]和Python的celery[3]。Go生态类似的还有machinery[4]和goworker 同时提供一个WebUI asynqmon[5],可以源码形式安装或使用Docker image, 还可以和Prometheus…...

保证率计算公式 正态分布
在正态分布中,如果我们要计算一个给定区间内的保证率,可以使用下面的计算公式: 找到给定保证率对应的标准正态分布的z值。可以使用标准正态分布表或计算器进行查询。例如,对于95%的保证率,对应的z值为1.96。 使用z值和…...
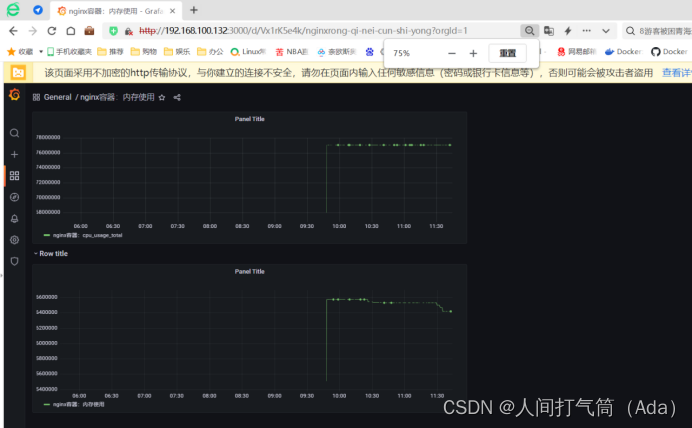
docker容器监控:Cadvisor+InfluxDB+Grafana的安装部署
目录 CadvisorInfluxDBGrafan安装部署 1、安装docker-ce 2、阿里云镜像加速器 3、下载组件镜像 4、创建自定义网络 5、创建influxdb容器 6、创建Cadvisor 容器 7、查看Cadvisor 容器: (1)准备测试镜像 (2)通…...

论文讲解——TPU-MLIR: A Compiler For TPU Using MLIR
论文讲解——TPU-MLIR: A Compiler For TPU Using MLIR https://arxiv.org/pdf/2210.15016.pdf概览模型转换TranslationCanonicalizeLoweringLayerGroup BufferizationCalibration QuantizationCorrectness Check相关资料 https://arxiv.org/pdf/2210.15016.pdf 本文将对TPU…...
基于最新导则下生态环评报告编制技术暨报告篇、制图篇、指数篇、综合应用篇系统性实践技能提升
查看原文>>>基于最新导则下生态环评报告编制技术暨报告篇、制图篇、指数篇、综合应用篇系统性实践技能提升 目录 专题一、生态环评报告编制规范 专题二、土地利用图 专题三、植被类型及植被覆盖度图 专题四、物种适宜生境分布图 专题五、生物多样性测定 专题六…...

NGZORRO:动态表单/模型驱动 的相关问题
官网的demo的[nzFor]"control.controlInstance",似乎是靠[formControlName]"control.controlInstance"来关联的。 <form nz-form [formGroup]"validateForm" (ngSubmit)"submitForm()"><nz-form-item *ngFor&quo…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
