LeetCode 350. 两个数组的交集 II
原题链接
难度:easy\color{Green}{easy}easy
题目描述
给你两个整数数组 nums1nums1nums1 和 nums2nums2nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]
提示:
- 1<=nums1.length,nums2.length<=10001 <= nums1.length, nums2.length <= 10001<=nums1.length,nums2.length<=1000
- 0<=nums1[i],nums2[i]<=10000 <= nums1[i], nums2[i] <= 10000<=nums1[i],nums2[i]<=1000
** 进阶 :**
- 如果给定的数组已经排好序呢?你将如何优化你的算法?
- 如果 nums1nums1nums1 的大小比 nums2nums2nums2 小,哪种方法更优?
- 如果 nums2nums2nums2 的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
算法
(排序双指针) O(n+m)O(n+m)O(n+m)
- 排序。
- 双指针遍历两个数组,如果 ·
nums1小,1的下标右移,nums2小2右移。 - 如果相等,加入目标数组,直到退出循环。
复杂度分析
-
时间复杂度:O(m+n)O(m + n)O(m+n)。
-
空间复杂度 : O(min(m+n))O(min(m + n))O(min(m+n))
C++ 代码
class Solution {
public:vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {sort(nums1.begin(), nums1.end());sort(nums2.begin(), nums2.end());vector<int> res;int left = 0, right = 0;while (left < nums1.size() && right < nums2.size()) {if (nums1[left] < nums2[right])left ++;else if (nums1[left] == nums2[right]) {res.push_back(nums1[left]);left ++, right ++;} else {right ++;}}return res; }
};
算法2
(集合)
- 使用数据结构
unordered_multiset存储nums1中的每个元素。 - 遍历数组
nums2,如果在 集合中,把该值加入答案,并且在集合中删除该值。
复杂度分析
- 时间复杂度:O(n)O(n)O(n)。
C++ 代码
class Solution {
public:vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {unordered_multiset<int> S;vector<int> res;for (int x : nums1) S.insert(x);for (int x : nums2)if (S.count(x)){res.push_back(x);S.erase(S.find(x));}return res;}
};
相关文章:

LeetCode 350. 两个数组的交集 II
原题链接 难度:easy\color{Green}{easy}easy 题目描述 给你两个整数数组 nums1nums1nums1 和 nums2nums2nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现…...

Python可以解码吗,解码打码是如何实现的
前言 咳咳,进来的铁汁都是抱着学习的心态进来看的吧,咱今天不讲解解码,咱来说说python如何来实现打码功能~ 这一个个进来的 都是标题党吧哈哈哈 有兴趣的可以继续看看哦 最近重温了一档综艺节目 至于叫什么 这里就不细说了 老是看着看着就…...
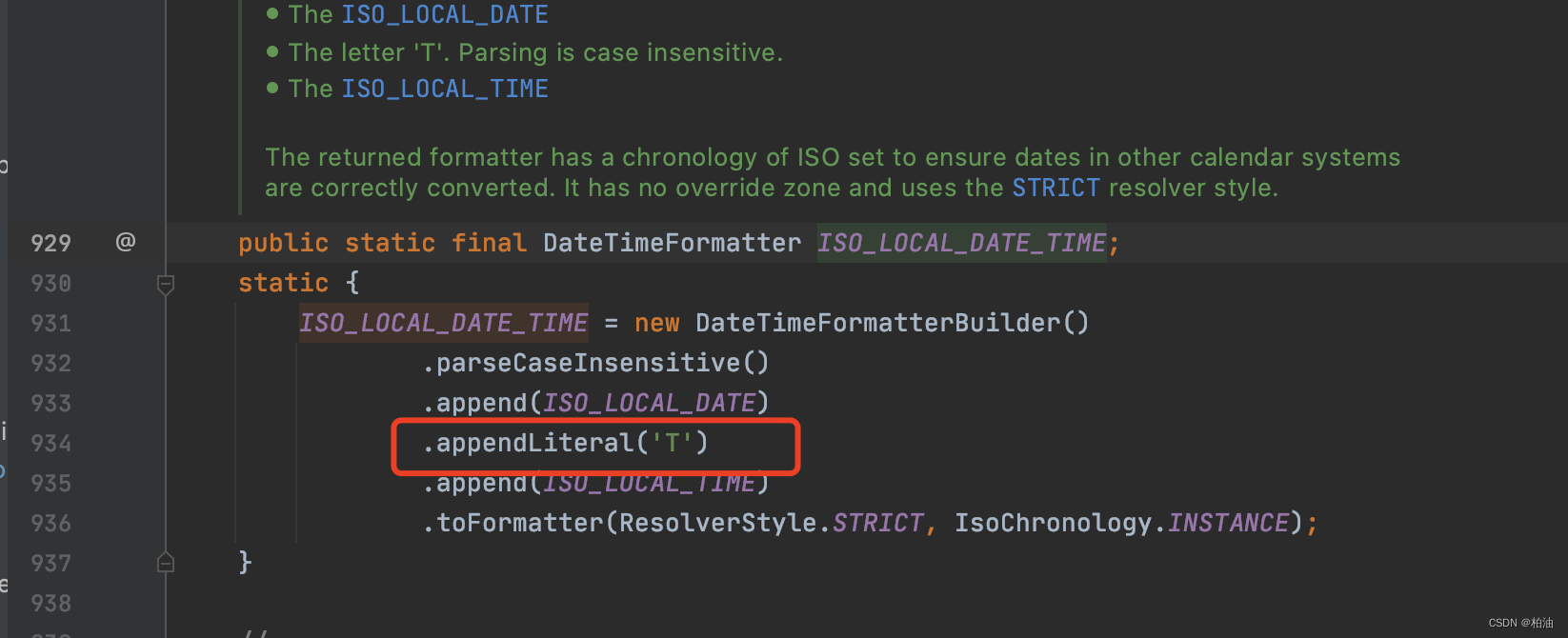
Jackson 序列化:Cannot deserialize value of type `java.time.LocalDateTime`
问题描述 使用 jackson 反序列化异常如下: Caused by: com.fasterxml.jackson.databind.exc.InvalidFormatException: Cannot deserialize value of type java.time.LocalDateTime from String “2023-02-13 19:43:01”: Failed to deserialize java.time.LocalDat…...
_习题)
机试_3_数据结构(一)_习题
数据结构(一)——练习题 学习完第三章-数据结构(一)之后,当然要做相应地练习啦~ 注:上述习题都可以在牛客进行测试。 例如,第2题链接:计算表达式_牛客题霸_牛客网 (nowcoder.com)…...

《Hadoop篇》------HDFS与MapReduce
目录 一、HDFS角色职责总结 二、CheckPoint机制 三、Mapreduce序列化 四、Mapper 4.1、官方介绍 4.2、Split计算 4.3、Split和block对应关系 4.4、启发式算法 五、MapTask整体的流程 六、压缩算法 6.1、压缩算法适用场景 6.2、压缩算法选择 6.2.1、Gzip压缩 6.2…...

网络爬虫简介
前言 没什么可以讲的所以就介绍爬虫吧 介绍 网络爬虫(英语:web crawler),也叫网路蜘蛛(spider),是一种用来自动浏览万维网的网络机器人。其目的一般为编纂网络索引。 网路搜索引擎等站点通过…...
通过4个月的自动化学习,现在我也拿到了25K的offer
毕业后的5年,是拉开职场差距的关键时期。有人通过这5年的努力,实现了大厂高薪,有人在这5年里得到贵人的赏识,实现了职级的快速拔升,还有人在这5年里逐渐掉队,成了职场里隐身一族,归于静默。 而…...

分库分表了解
数据切分根据其切分类型,可以分为两种方式:垂直(纵向)切分和水平(横向)切分一:垂直(纵向)切分【基于表或字段划分,表结构不同】1:垂直分库根据业务…...
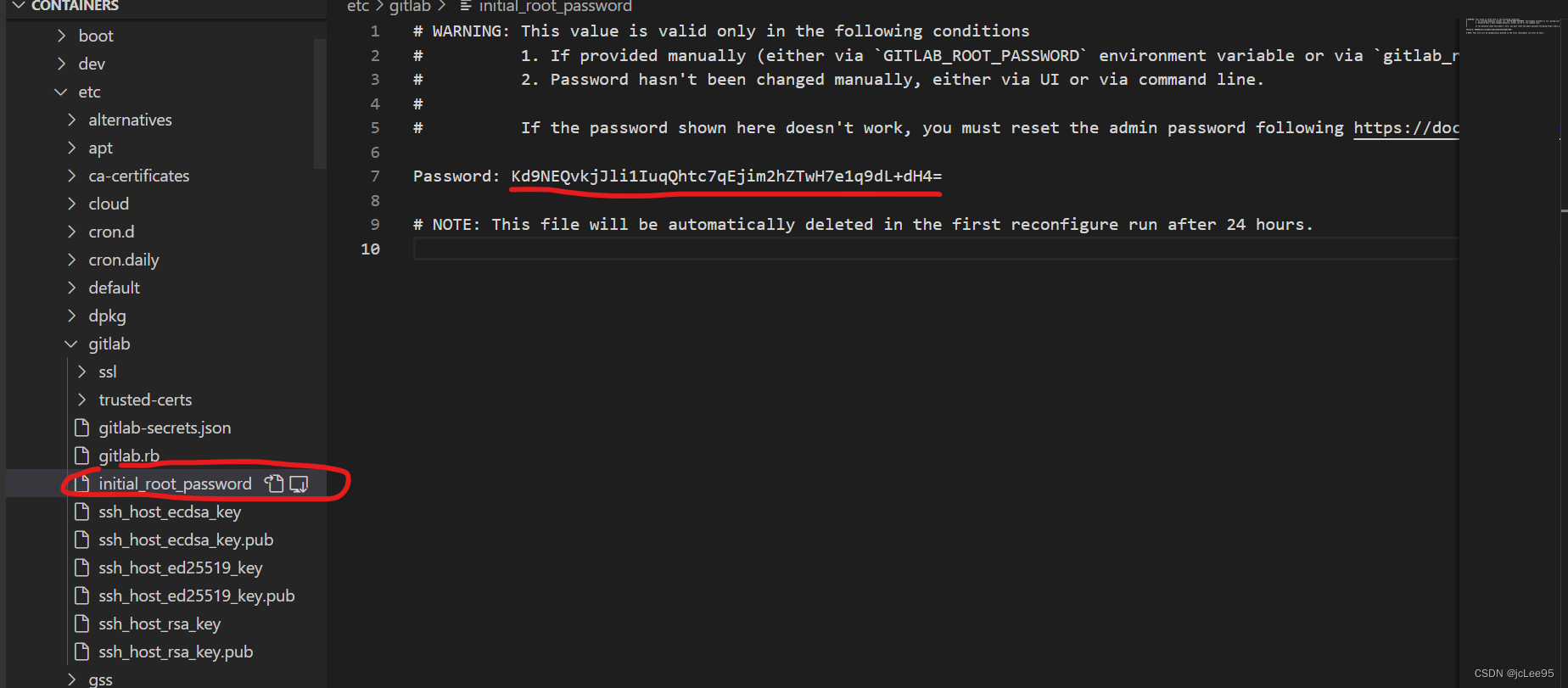
docker中 gitlab 安装、配置和初始化
小笔记:gitlab配置文件 /etc/gitlab/gitlab.rb 配置项jcLee95 的CSDN博客:https://blog.csdn.net/qq_28550263?spm1001.2101.3001.5343 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/1…...

有哪些好用的C++Json库?
文章目录RapidJSONJSON for Modern CBoost.PropertyTreeJanssonPicoJSONC REST SDKnlohmann json(ky用的这个)jsoncpp(cw用的这个)RapidJSON RapidJSON是一个快速、高效的C JSON解析器和生成器,支持SAX和DOM两种解析模…...

Docker 快速上手学习入门教程
目录 1、docker 的基础概念 2、怎样打包和运行一个应用程序? 3、如何对 docker 中的应用程序进行修改? 4、如何对创建的镜像进行共享? 5、如何使用 volumes 名称对容器中的数据进行存储?// 数据挂载 6、另一种挂载方式&…...
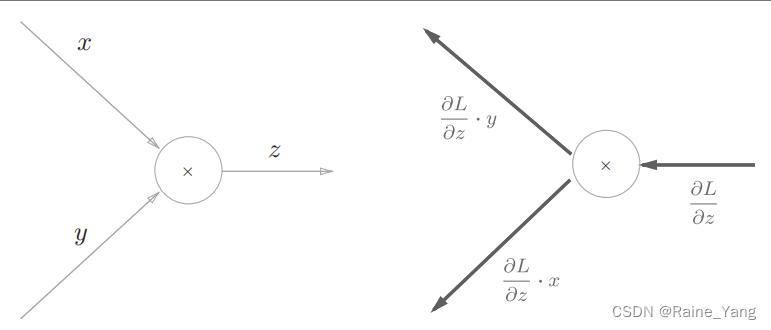
深度学习笔记:误差反向传播(1)
1 计算图 计算图使用图(由节点和边构成的图)来表达算式。 如图,我们用节点代表运算符号,用边代表传入的参数,即可算出购买苹果和橘子的总价格。 2 计算图的局部计算 局部计算意味着每个节点只处理和其相关的运算&…...
锁相环(1)
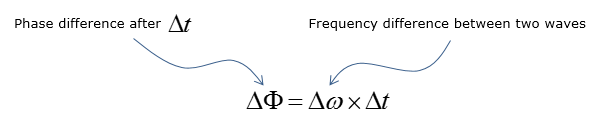
PLL代表相位锁定环。顾名思义,如下图所示,PLL是一种具有反馈循环的电路,可将反馈信号的相/频率保持与参考输入信号的相/频率相同(锁定)。 如下图所示,如果参考输入和反馈输入之间存在相位差,则…...

2023金三银四跳槽必会Java核心知识点笔记整理
现在互联网大环境不好,互联网公司纷纷裁员并缩减 HC,更多程序员去竞争更少的就业岗位,整的 IT 行业越来越卷。身为 Java 程序员的我们就更不用说了,上班 8 小时需要做好本职工作,下班后还要不断提升技能、技术栈&#…...

二十四节气—雨水,好雨知时节,当春乃发生。
雨水,是二十四节气之第2个节气。 雨水节气不仅表明降雨的开始及雨量增多,而且表示气温的升高,意味着进入气象意义的春天。 雨水节是一个非常富有想象力和人情味的节气,在这一天,不管下不下雨都充满着一种雨意蒙蒙的诗…...

为什么要使用数据库?
随着互联网技术的高速发展,预计2020 年底全世界网民的数量将达到 50 亿。网民数量的增加带动了网上购物、微博,网络视频等产业的发展。那么,随之而来的就是庞大的网络数据量。 大量的数据正在不断产生,那么如何安全有效地存储、检…...

【原创】java+swing+mysql图书管理系统设计与实现
图书管理系统是一个比较常见的系统,今天我们主要介绍如何使用javaswiingmysql去开发一个cs架构的图书管理系统,方便学生进行图书借阅。 功能分析: 宿舍报修管理系统的使用角色,一般分为管理员和学生,管理员主要进行学…...

图论 —— 强连通分量
概念 连通图 无向图 G G G 中,若对任意两点 V i , V j V_i, V_j V<...
:物理层和链路层,通道复用,MAC地址,CSMA/CD协议,PPP点对点协议)
计算机网络(二):物理层和链路层,通道复用,MAC地址,CSMA/CD协议,PPP点对点协议
文章目录一、物理层主机之间的通信方式通道复用技术常见的宽带接入技术二、链路层MAC地址和IP地址分别有什么作用为什么有了MAC地址之后还需要IP地址为什么有了IP地址还需要MAC地址以太网中的CSMA/CD协议数据链路层上的三个基本问题PPP协议一、物理层 主机之间的通信方式 单工…...

英语基础-定语从句的特殊用法及写作应用
1. 定语从句的引导词省略的情况 1. that 引导定语从句,从句中缺宾语/表语,that可省略; This is the book that he likes. I like the shirt that you gave me. We do not agree on the plan that you make. China is not the country th…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
