AES加密(1):AES基础知识和计算过程
从产品代码的安全角度考虑,我们需要对代码、数据进行加密。加密的算法有很多种,基于速度考虑,我们一般使用对称加密算法,其中有一种常见的对称加密算法:AES(Advanced Encryption Standard)。在一些高端的MCU,如I.MX RT1176中,AES直接集成到了硬件中,它有一个OTFAD实时解密引擎,可以将保存在NOR Flash中使用AES加密的代码边解密边运行,可见AES加密的可靠性和重要性。所以本节就来介绍一下AES加密算法的原理。
文章目录
- 1 简介
- 2 AES算法
- 2.1 AES如何工作
- 2.2 AES计算步骤
- 2.3 实例
- 3 总结
1 简介
AES加密算法(也称为Rijndael算法)是一种对称分块密码算法,以块为单位对数据进行加密,一个块的大小为128位。而AES的密钥则可以为128、192和256位。不同的密钥长度对应着不同的加密轮数:128位为10轮、192位为12轮、256位为14轮。AES基于替代-置换网络,也称为SP网络。它由一系列链接操作组成,包括将输入替换为特定的输出(替代)以及涉及位排序(置换)的其他操作。
AES有如下特点:
SP网络:与DES算法中的Feistel密码结构不同,它采用了SP网络结构。- 密钥扩展:在第一阶段,它仅采用一个密钥,然后扩展为用于各个轮次的多个密钥
- 字节数据:AES加密算法对字节数据进行操作,而不是位数据。在加密过程中,将128位块大小视为16个字节。
- 密钥长度:要执行的轮次取决于用于加密数据的密钥长度。128位密钥长度有十轮,192位密钥长度有12轮,256位密钥长度有14轮。
2 AES算法
2.1 AES如何工作
要理解AES的工作方式,首先需要了解它是如何在多个步骤之间传输数据的。由于单个块是16字节,因此我们用一个4x4矩阵(也叫状态数组)保存数据,每个单元保存1个字节的信息。

对于128位的密钥,加密过程中需要执行16轮操作。每一轮操作都需要使用一个不同的轮密钥。轮密钥是通过对初始密钥进行一系列变换生成的,这个在后面的例子中详细介绍。根据AES标准规定,对于128位密钥,需生成10个轮密钥,用于不同轮次的AES加密操作。
2.2 AES计算步骤
流程图如下:
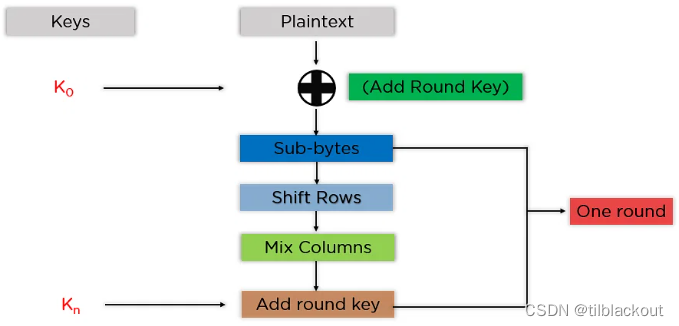
这些步骤需要依次对每个块进行操作。成功加密每个块后,将它们组合在一起形成最终的密文。具体步骤如下:
(1)添加轮密钥(Add Round Key)
使用生成的第一个密钥(K0),通过与状态数组中存储的块数据进行异或运算。将得到的状态数组作为下一步的输入。
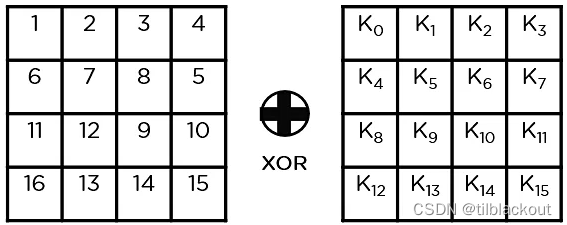
(2)字节替换(Sub-Bytes)
在这个步骤中,将状态数组的每个字节转换为十六进制,分为两个4位的数。通过一个替代盒(S-Box)映射生成最终状态数组的新值,其中高四位(行数)和低四位(列数)作为索引,在S-Box中查找对应的字节进行替换。
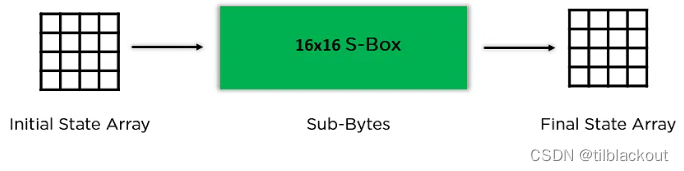
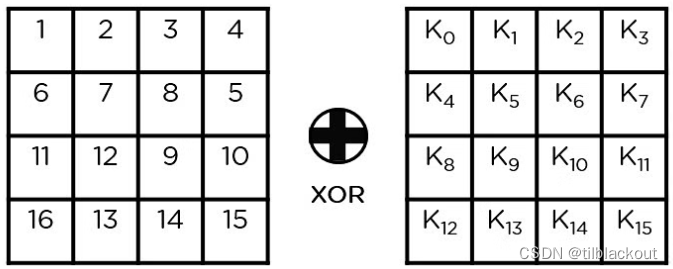
(3)行移位(Shift Rows)
它交换行元素之间的位置。第一行不动,第二行循环左移1位,第三行循环左移2位,第四行循环左移3位。
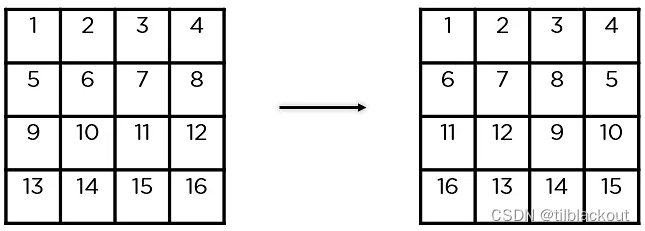
(4)列混合变换(Mix Columns)
将一个预定义的常数矩阵与状态数组中的每一列进行乘法运算,从而得到下一状态数组中的新列。通过对状态数组中的所有列都执行与相同常数矩阵的乘法运算,最终得到下一步的状态数组。这个步骤在最后一轮中不执行。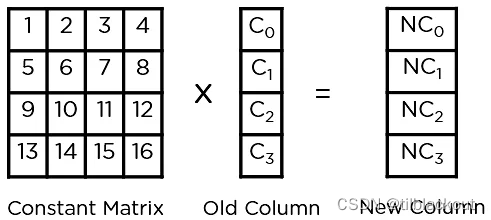
- 注意:这里的运算并不是传统的矩阵乘法,这个在后面的例子中讲解
(5)添加轮密钥(Add Round Key)
将轮次对应的密钥与前一步得到的状态数组进行异或运算。如果这是最后一轮,则得到的状态数组将成为特定块的密文;否则,它将作为下一轮的新状态数组输入。
2.3 实例
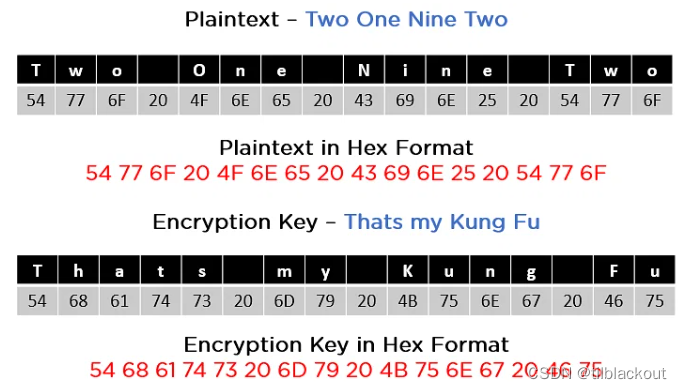
假设明文为Two One Nine Two,而加密密钥为Thats my Kung fu,我们需要使用它们的16进制来进行计算,它们的长度都是128bit,如下图所示:
接着我们生成接下来10轮的扩展密钥(轮密钥):

所有的轮密钥都是从Round 0密钥进行扩展的,首先将每一列从0开始索引:

我们根据以下公式可以一列一列地求出后面的轮密钥:
如果这个索引不是4的倍数,则 W i = W i − 4 ⊕ W i − 1 W_i=W_{i-4} \oplus W_{i-1} Wi=Wi−4⊕Wi−1。
如果索引是4的倍数,则 W i = W i − 4 ⊕ T ( W i − 1 ) W_i=W_{i-4} \oplus T(W_{i-1}) Wi=Wi−4⊕T(Wi−1)。其中T函数包括:
①字循环:假设 W i − 1 W_{i-1} Wi−1从上到下为 [ a 1 , a 2 , a 3 , a 4 ] [a_1,a_2,a_3,a_4] [a1,a2,a3,a4],则字循环后为 [ a 2 , a 3 , a 4 , a 1 ] [a_2,a_3,a_4,a_1] [a2,a3,a4,a1]
②字节代换:将字循环的结果使用S盒进行字节代换
③轮常量异或:将字循环的结果、字节代换的结果和轮常量三者进行异或得到最终的 T ( W i − 1 ) T(W_{i-1}) T(Wi−1),其中轮常量是一个固定的10×4的矩阵
(1)添加轮密钥(Add Round Key)
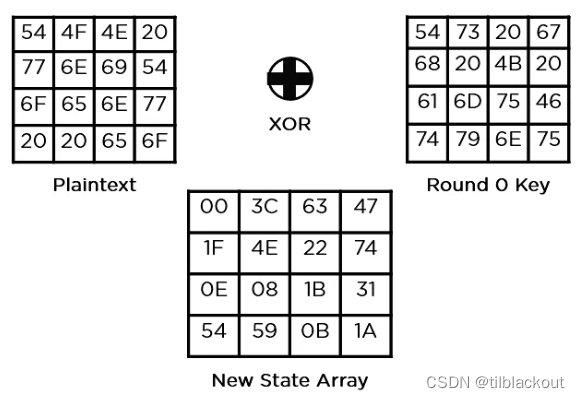
(2)字节替换(Sub-Bytes):通过一个16x16的S-Box进行字节替换
这里就不列出S-Box的原型了,假设最终的结果如下:
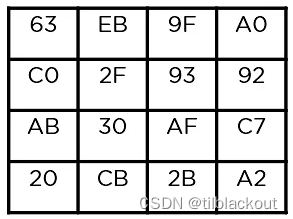
(3)行移位(Shift Rows)
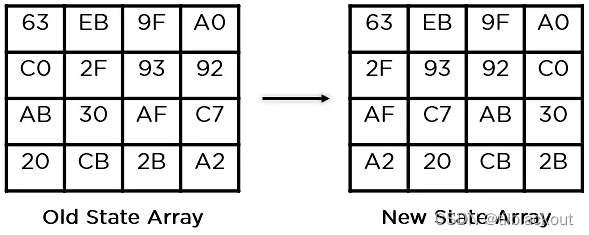
(4)列混合变换(Mix Columns)
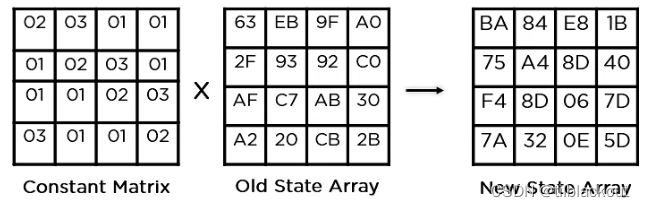
这里以得出状态矩阵的第一个元素0xBA为例,看看是怎么计算得到的:
res = ( 2 × 0 x 63 ) + ( 3 × 0 x 2 F ) + 0 x A F + 0 x A 2 = 0 x B A \text { res }=(2\times0\text{x}63)+(3 \times0\text{x}2 F)+0\text{x}A F+0\text{x}A 2=0\text{x}B A res =(2×0x63)+(3×0x2F)+0xAF+0xA2=0xBA
根据AES的规定,这里有两个地方需要转化:第一个加法需要转为异或运算,第二个乘法的运算的转换有些复杂,规则如下:
( 00000010 ) × ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = { ( a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 ) , a 7 = 0 ( a 6 a 5 a 4 a 3 a 2 a 1 a 0 0 ) ⊕ ( 00011011 ) , a 7 = 1 ( 00000011 ) × ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = [ ( 00000010 ) ⊕ ( 00000001 ) ] × ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) = [ ( 00000010 ) × ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) ] ⊕ ( a 7 a 6 a 5 a 4 a 3 a 2 a 1 a 0 ) \begin{aligned} & (00000010) \times\left(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0\right)=\left\{\begin{array}{c} \left(a_6 a_5 a_4 a_3 a_2 a_1 a_0 0\right), a_7=0 \\ \left(a_6 a_5 a_4 a_3 a_2 a_1 a_0 0\right) \oplus(00011011), a_7=1 \end{array}\right. \\ & (00000011) \times\left(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0\right)=[(00000010) \oplus(00000001)] \times\left(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0\right) \\ & =\left[(00000010) \times\left(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0\right)\right] \oplus\left(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0\right) \end{aligned} (00000010)×(a7a6a5a4a3a2a1a0)={(a6a5a4a3a2a1a00),a7=0(a6a5a4a3a2a1a00)⊕(00011011),a7=1(00000011)×(a7a6a5a4a3a2a1a0)=[(00000010)⊕(00000001)]×(a7a6a5a4a3a2a1a0)=[(00000010)×(a7a6a5a4a3a2a1a0)]⊕(a7a6a5a4a3a2a1a0)
乘法运算需要将数转化为二进制,上图中第一个公式为2乘以一个uint8的数的规则。第二行为3乘以一个uint8的数的规则,实际上就是根据乘法分配率转变为第一个公式。
我们现在就来计算一下上面的两个乘法:
2 × 0 x 63 = ( 00000010 ) b × ( 01100011 ) b = ( 11000110 ) b = 0 × C 6 3 × 0 x 2 F = [ ( 00000010 ) b × ( 00101111 ) b ] ⊕ ( 0010111 ) b = ( 01011110 ) b ⊕ ( 00101111 ) b = ( 01110001 ) b = 0 × 71 res = 0 x C 6 ⊕ 0 x 71 ⊕ 0 x A F ⊕ 0 x A 2 = 0 x B A \begin{aligned} & 2\times0\text{x}63=(00000010) b\times(01100011) b=(11000110) b=0 \times C 6 \\ & 3\times0\text{x}2 F=\left[(00000010) b\times(00101111) b\right]\oplus(0010111) b=(01011110) b\oplus(00101111) b=(01110001) b=0 \times 71 \\ & \text { res }=0\text{x}C 6\oplus0 \text{x}71\oplus 0\text{x}A F{ }\oplus 0\text{x}A 2=0 \text{x}B A \end{aligned} 2×0x63=(00000010)b×(01100011)b=(11000110)b=0×C63×0x2F=[(00000010)b×(00101111)b]⊕(0010111)b=(01011110)b⊕(00101111)b=(01110001)b=0×71 res =0xC6⊕0x71⊕0xAF⊕0xA2=0xBA
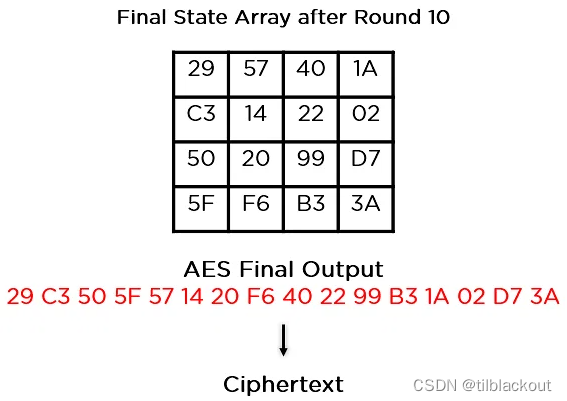
(5)添加轮密钥(Add Round Key):这一步异或上前面的Round 1密钥
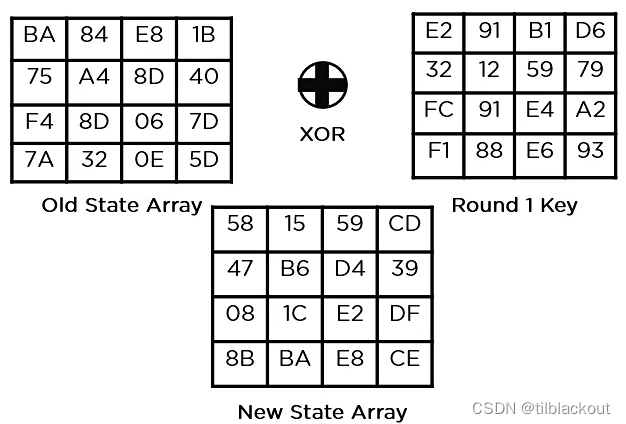
这个状态数组将成为下一轮的输入,根据密钥的长度,重复上述步骤,直到完成第10轮,就得到了最终的密文。
3 总结
AES算法用于加密与解密数据,在计算机领域中具有高度的安全性和效率。AES算法的数据块大小为128位,密钥长度可以是128位、192位或256位。算法在加密过程中使用了不同的轮数,这些轮数也根据密钥长度的不同而有所变化。本文对AES加密的原理做了一个简单的介绍,并举了一个简单的例子。和我之前写的CRC、MD5的博客一样,有了原理后一定要在代码中实现,这才是理论的意义,这也能帮我们更深入地理解代码。所以下一节,我将深入地剖析一下AES的代码实现。
相关文章:

AES加密(1):AES基础知识和计算过程
从产品代码的安全角度考虑,我们需要对代码、数据进行加密。加密的算法有很多种,基于速度考虑,我们一般使用对称加密算法,其中有一种常见的对称加密算法:AES(Advanced Encryption Standard)。在一些高端的MCU࿰…...
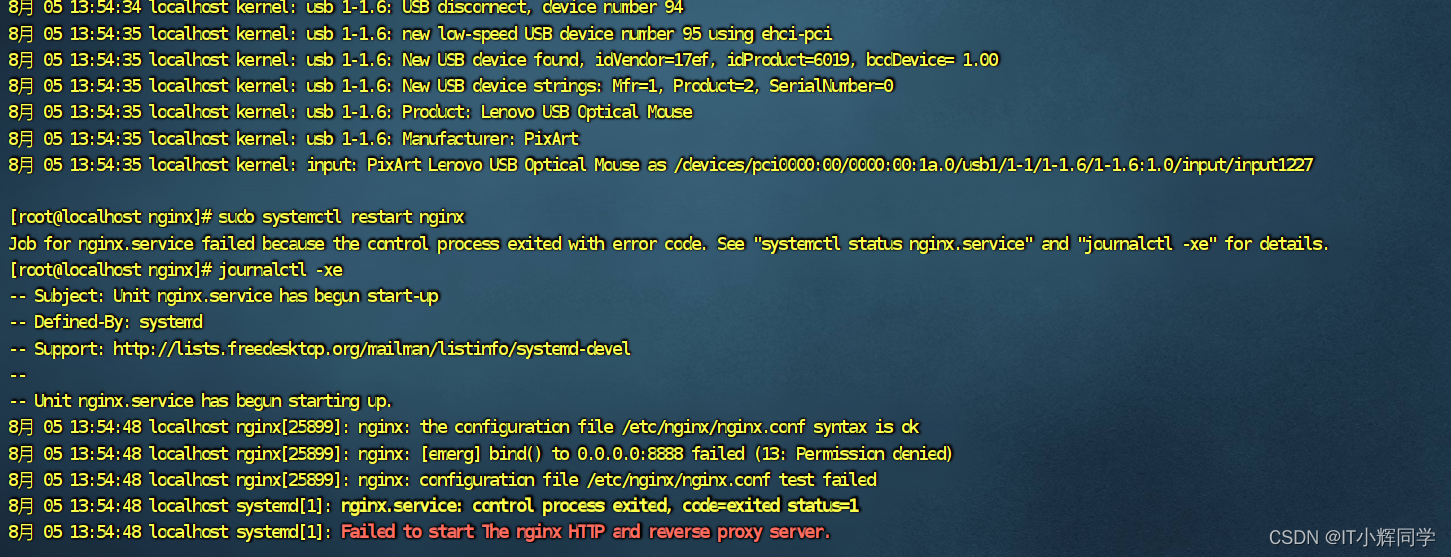
Nginx启动报错- Failed to start The nginx HTTP and reverse proxy server
根据日志,仍然出现 “bind() to 0.0.0.0:8888 failed (13: Permission denied)” 错误。这意味着 Nginx 仍然无法绑定到 8888 端口,即使使用 root 权限。 请执行以下操作来进一步排查问题: 确保没有其他进程占用 8888 端口:使用以…...

五、web应用程序技术——web功能
文章目录 一、服务器端功能1.1 SQL1.2 XML1.3 web服务 二、客户端功能2.1 HTML2.2 超链接2.3 表单2.4 CSS2.5 JavaScript2.6 文档对象模型2.7 Ajax2.8 JSON2.9 同源策略2.10浏览器拓展技术 一、服务器端功能 早期的web站点由各种静态资源组成,如HTML页面与图片。当用…...
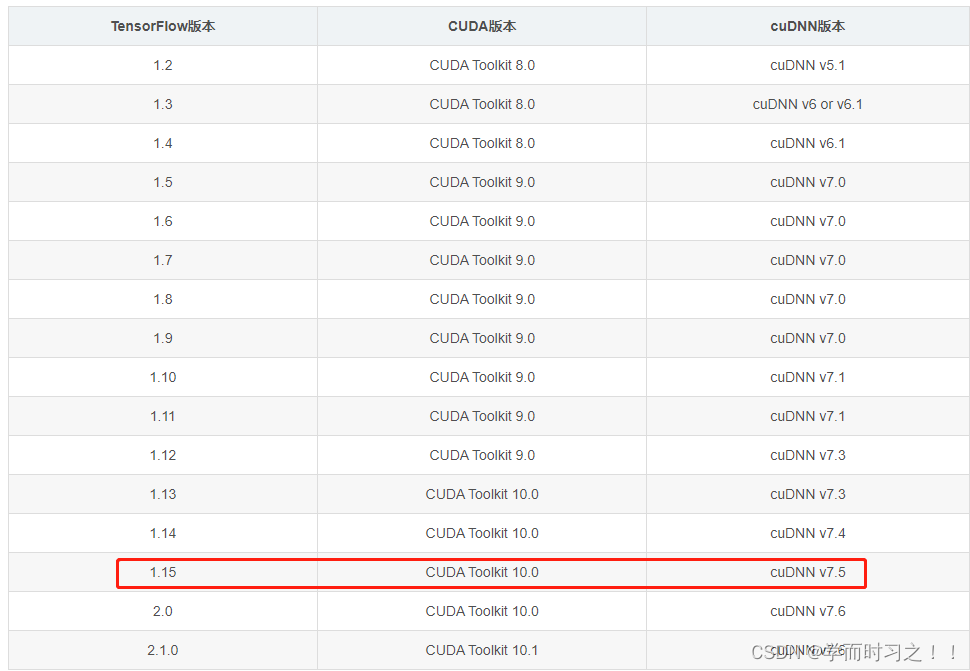
AutoDL服务器的镜像版本太高,配置python3.7 tensorflow1.15版本的框架的步骤
1.选择一个实例,进入后端界面 2. 更新bashrc中的环境变量 conda init bash && source /root/.bashrc查看虚拟环境 conda info --envs可以看到此时有一个base的虚拟环境 但是它的python版本为3.8.10,无法安装tensorflow1.15,所以我们要创建一个…...

c++ boost库之scoped_ptr,shared_ptr,weak_ptr智能指针
头文件: #include <boost/smart_ptr.hpp> #include <boost/make_shared.hpp> #include <boost/shared_ptr.hpp> 1. scoped_ptr & scoped_array 只能在本作用域内使用,不希望被转让; 效率等同原始指针; scoped_ptr<string> sp(new string("t…...
)
【leetcode】383. 赎金信(easy)
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字符只能在 ransomNote 中使用一次。 class Solution {public boolea…...
CTF-记一次PWN练习
PWN是一个黑客语法的俚语词,自"own"这个字引申出来的,这个词的含意在于,玩家在整个游戏对战中处在胜利的优势,或是说明竞争对手处在完全惨败的情形下,这个词习惯上在网络游戏文化主要用于嘲笑竞争对手在整个…...

《golang设计模式》第一部分·创建型模式-04-工厂方法模式(Factory Method)
文章目录 1 概述2.1 角色2.2 类图 2 代码示例2. 1 设计2.2 代码2.3 类图 3. 简单工厂3.1 角色3.2 类图3.3 代码示例3.3.1 设计3.3.2 代码3.3.3 类图 1 概述 工厂方法类定义产品对象创建接口,但由子类实现具体产品对象的创建。 2.1 角色 Product(抽象产…...
redis的配置和使用、redis的数据结构以及缓存遇见的常见问题
目录 1.缓存 2.redis不仅仅可以做缓存,只不过说他的大部分场景,是做缓存。本地缓存重启后缓存里的东西就没有了,但是redis有。 3.redis有几个特性:查询快,但是是放到内存里的〈断电或者重启,数据就丢了),…...

在Ubuntu系统下修改limits.conf不生效
文章目录 前言尝试过程总结 前言 最近遇到的一个问题,在Ubuntu系统下修改/etc/security/limits.conf不生效,查了多种资料都说不用重启,但是我改完就是不生效,多次尝试之后发现Ubuntu系统有毒。 尝试过程 通过 ulimit -n 命令可…...

selenium 选项 chrome_options
当前环境: Windows 10 Python 3.7 selenium 3.141.0 Google Chrome 115.0.5790.110 (64 位) 一种方法: from selenium import webdriverif __name__ __main__:# chrome 选项配置chrome_options webdriver.ChromeOptions(…...
)
自然语言处理(Natural Language Processing,NLP)
自然语言处理(Natural Language Processing,NLP)是人工智能领域的一个重要分支,旨在使计算机能够理解、处理和生成人类自然语言。NLP 的目标是让计算机能够像人类一样有效地理解和交流,从而实现更自然、更智能的人机交互。 NLP的理解概括&…...
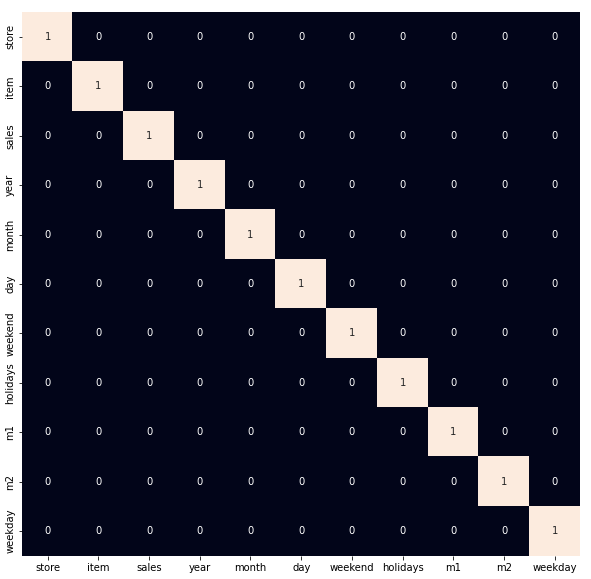
基于机器学习的库存需求预测 -- 机器学习项目基础篇(12)
在本文中,我们将尝试实现一个机器学习模型,该模型可以预测在不同商店销售的不同产品的库存量。 导入库和数据集 Python库使我们可以轻松地处理数据,并通过一行代码执行典型和复杂的任务。 Pandas -此库有助于以2D阵列格式加载数据帧&#…...
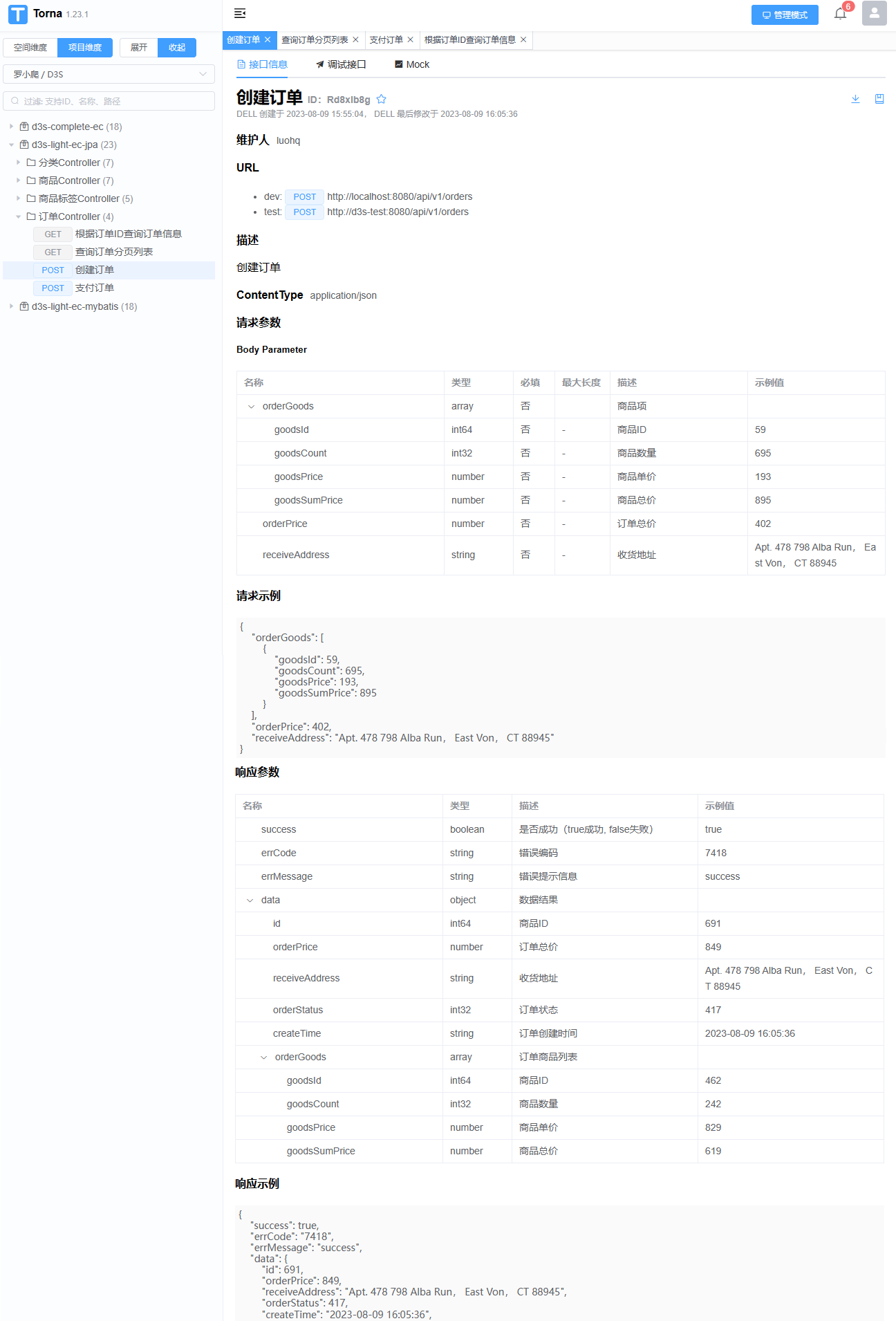
【D3S】集成smart-doc并同步配置到Torna
目录 一、引言二、maven插件三、smart-doc.json配置四、smart-doc-maven-plugin相关命令五、推送文档到Torna六、通过Maven Profile简化构建 一、引言 D3S(DDD with SpringBoot)为本作者使用DDD过程中开发的框架,目前已可公开查看源码&#…...
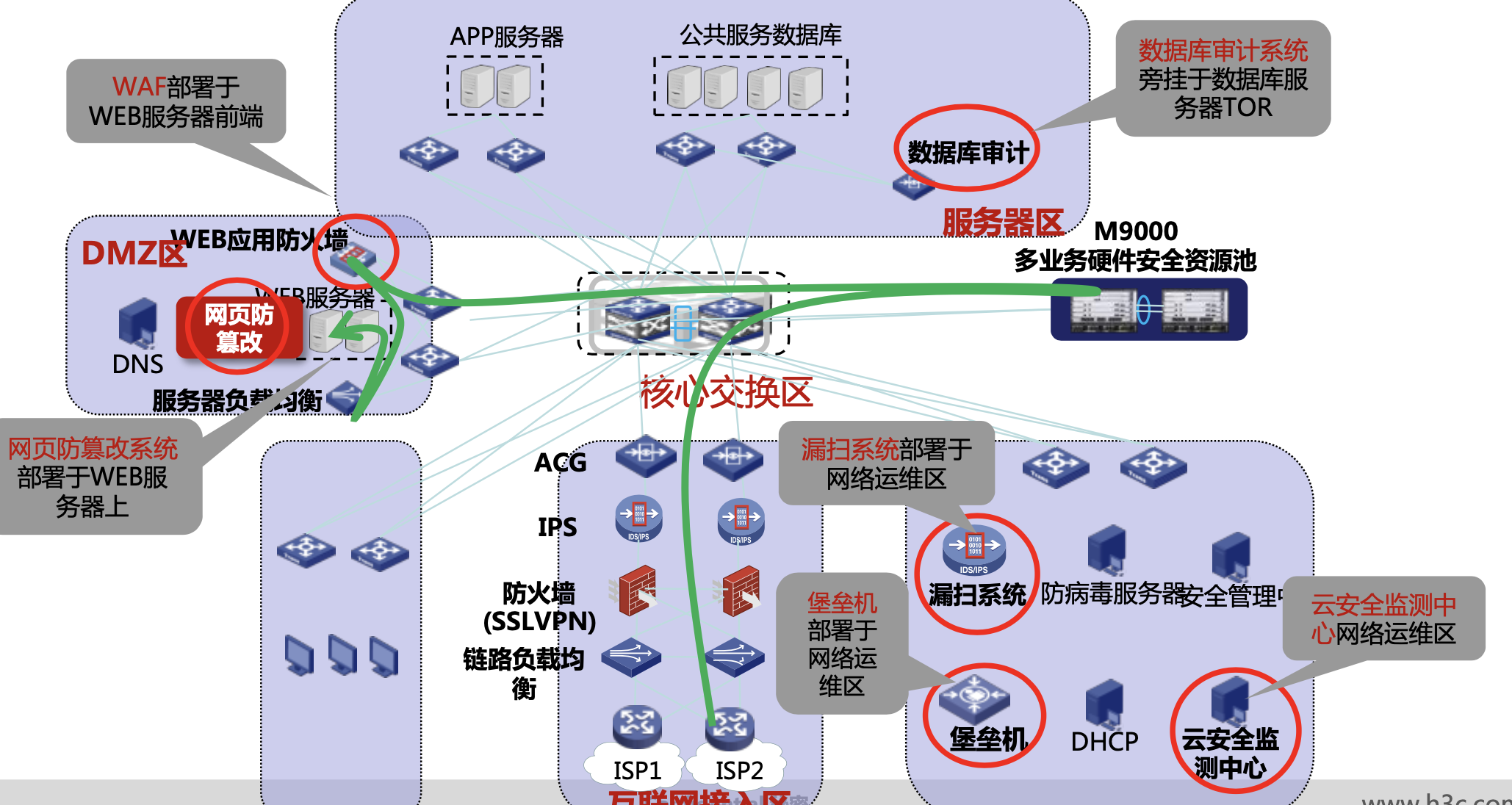
网络安全设备及部署
什么是等保定级? 之前了解了下等保定级,接下里做更加深入的探讨 文章目录 一、网路安全大事件1.1 震网病毒1.2 海康威视弱口令1.3 物联网Mirai病毒1.4 专网 黑天安 事件1.5 乌克兰停电1.6 委内瑞拉电网1.7 棱镜门事件1.8 熊猫烧香 二、法律法规解读三、安…...
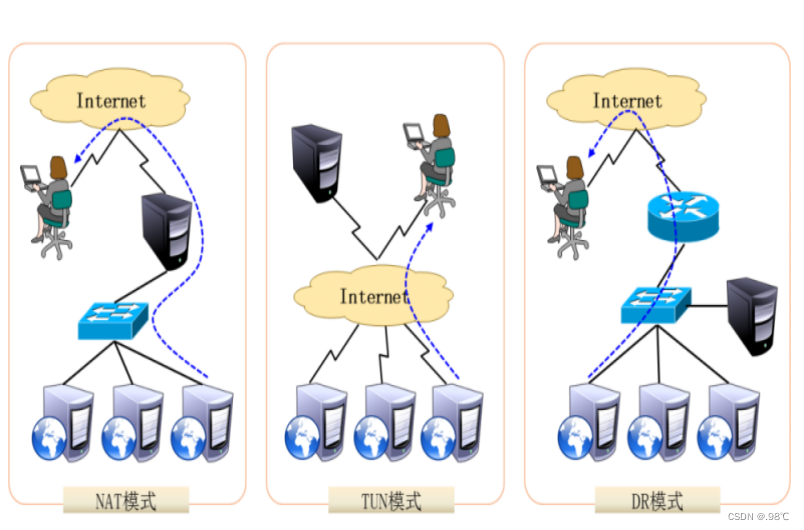
LVS集群
目录 1、lvs简介: 2、lvs架构图: 3、 lvs的工作模式: 1) VS/NAT: 即(Virtual Server via Network Address Translation) 2)VS/TUN :即(Virtual Server v…...
从入门到精通系列之十二:安装和设置 kubectl)
Kubernetes(K8s)从入门到精通系列之十二:安装和设置 kubectl
Kubernetes K8s从入门到精通系列之十二:安装和设置 kubectl 一、kubectl二、在 Linux 系统中安装并设置 kubectl1.准备工作2.用 curl 在 Linux 系统中安装 kubectl3.用原生包管理工具安装 三、验证 kubectl 配置四、kubectl 的可选配置和插件1.启用 shell 自动补全功…...
探索 TypeScript 元组的用例
元组扩展了数组数据类型的功能。使用元组,我们可以轻松构造特殊类型的数组,其中元素相对于索引或位置是固定类型的。由于 TypeScript 的性质,这些元素类型在初始化时是已知的。使用元组,我们可以定义可以存储在数组中每个位置的数…...

Pytorch使用NN神经网络模型实现经典波士顿boston房价预测问题
Pytorch使用多层神经网络模型实现经典波士顿boston房价预测问题 波士顿房价数据集介绍 波士顿房价数据集是一个经典的机器学习数据集,用于预测波士顿地区房屋的中位数价格。该数据集包含了506个样本,每个样本有13个特征,包括城镇的各种指标&…...
微服务间消息传递
微服务间消息传递 微服务是一种软件开发架构,它将一个大型应用程序拆分为一系列小型、独立的服务。每个服务都可以独立开发、部署和扩展,并通过轻量级的通信机制进行交互。 应用开发 common模块中包含服务提供者和服务消费者共享的内容provider模块是…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
