AcWing 1564:哈希 ← 只具有正增量的二次探测法
【题目来源】
https://www.acwing.com/problem/content/1566/
【题目描述】
将一个由若干个不同正整数构成的整数序列插入到一个哈希表中,然后输出输入数字的位置。
哈希函数定义为 H(key)=key%TSize,其中 TSize 是哈希表的最大大小。
利用只具有正增量的二次探测法来解决冲突。
注意,哈希表的大小最好是素数,如果用户给出的最大大小不是素数,则必须将表大小重新定义为大于用户给出的大小的最小素数。
【输入格式】
第一行包含两个整数 MSize 和 N,分别表示用户定义的表的大小以及输入数字的数量。
第二行包含 N 个不同的正整数,数字之间用空格隔开。
【输出格式】
在一行中,输出每个输入数字的相应位置(索引从 0 开始),数字之间用空格隔开,行尾不得有多余空格。
如果无法插入某个数字,则输出 -。
【数据范围】
1≤MSize≤10^4,
1≤N≤MSize,
输入数字均在 [1,10^5] 范围内。
【输入样例】
4 4
10 6 4 15
【输出样例】
0 1 4 -
【算法分析】
本算法涉及多个细节,分述如下:
** 散列表(哈希表)
散列表,即哈希表,是根据给定关键字(Key)来计算出该关键字在表中存储地址的数据结构。也就是说,散列表建立了关键字与存储地址之间的一种直接映射关系。将关键字映射到表中记录的地址,这加快了查找速度。
模拟实现散列表的代码,详见:https://blog.csdn.net/hnjzsyjyj/article/details/132179868
** 二次探测法
本题陈述表示采用“只具有正增量的二次探测法”解决冲突。
所谓“只具有正增量的二次探测法”,即 p=(H(key)+di*di) mod m 。其中:
m 为哈希表长度;
di 为增量序列 1^2,2^2,3^2,…,k^2(k≤m-1);
H(key) 为哈希函数,常采用“除留余数法”构造,即 H(key)=key%p 。除留余数法,方便编程实现。一般情况下,常选 p 为小于哈希表长度 m 的最大质数。
求小于给定数的最大素数代码,参见:https://blog.csdn.net/hnjzsyjyj/article/details/127699346
** 大于给定数的最小素数
由于本题有段陈述“哈希表的大小最好是素数,如果用户给出的最大大小不是素数,则必须将表大小重新定义为大于用户给出的大小的最小素数”,所以需要判断给定的数 MSize 是否为素数,若不是,则需要求大于给定的数 MSize 的最小素数。
求大于给定数的最小素数的代码详见:
https://blog.csdn.net/hnjzsyjyj/article/details/132182788
#include <bits/stdc++.h>
using namespace std;bool isPrime(int n) {if(n==1) return false;for(int i=2; i<=sqrt(n); i++) {if(n%i==0) return false;}return true;
}int getPrime(int n) { //Get least prime bigger than nfor(int i=n+1; ;i++) {if(isPrime(i)) {return i;break;}}
}int main(){int n;cin>>n;cout<<getPrime(n)<<endl;return 0;
}/*
in:100
out:101in:1000
out:1009
*/
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=1e4+5;
int h[maxn];
int msize,n;bool isPrime(int x) {if(x==1) return false;for(int i=2; i<=sqrt(x); i++) {if(x%i==0) return false;}return true;
}int getPrime(int x) { //Get least prime bigger than nfor(int i=x+1; ; i++) {if(isPrime(i)) {return i;break;}}
}int find(int x) {int t=x%msize;for(int k=0; k<msize; k++) { //二次探测法int p=(t+k*k)%msize;if(!h[p]) return p;}return -1;
}int main() {scanf("%d %d",&msize,&n);if(!isPrime(msize)) msize=getPrime(msize);for(int i=0; i<n; i++) {int x;scanf("%d",&x);int t=find(x);if(t==-1) printf("-");else {h[t]=x;printf("%d",t);}if(i!=n-1) printf(" ");}return 0;
}/*
in:
4 4
10 6 4 15out:
0 1 4 -
*/
【参考文献】
https://blog.csdn.net/qq_43733499/article/details/120093683
https://www.acwing.com/solution/content/55930/
相关文章:

AcWing 1564:哈希 ← 只具有正增量的二次探测法
【题目来源】https://www.acwing.com/problem/content/1566/【题目描述】 将一个由若干个不同正整数构成的整数序列插入到一个哈希表中,然后输出输入数字的位置。 哈希函数定义为 H(key)key%TSize,其中 TSize 是哈希表的最大大小。 利用只具有正增量的二…...
什么是媒体代发布?媒体代发布注意事项
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 媒体代发布是指将新闻稿或其他宣传内容委托给专业的媒体代理机构或公司进行发布和推广的活动。这些机构通常拥有丰富的媒体资源、人脉和经验,能够更好地将信息传递给目标受众…...

docker版jxTMS使用指南:使用jxTMS采集数据之二
本文是如何用jxTMS进行数据采集的第二部分,整个系列的文章请查看:docker版jxTMS使用指南:4.4版升级内容 docker版本的使用,请查看:docker版jxTMS使用指南 4.0版jxTMS的说明,请查看:4.0版升级内…...

系列六、Springboot操作RocketMQ
一、同步消息 1.1、发送&接收简单消息 1.1.1、发送简单消息 /*** 测试发送简单消息*/ Test public void sendSimpleMessage() {SendResult result rocketMQTemplate.syncSend("BOOT_TOPIC_SIMPLE", "我是一个简单消息");// 往[BOOT_TOPIC_SIMPLE]主…...

【jupyter异常错误】Kernel started:No module named ipykernel_launcher
尝试过的方案 pip install ipykernel 执行之后提示已经安装,但是执行代码依然报错 解决方案 python -m pip install ipykernel -U --force-reinstall 相当于是强制重新安装 安装成功后没有报错 注:根本原因应该是原来安装的包存在问题,虽然检测出来已经存在…...

使用langchain与你自己的数据对话(五):聊天机器人
之前我已经完成了使用langchain与你自己的数据对话的前四篇博客,还没有阅读这四篇博客的朋友可以先阅读一下: 使用langchain与你自己的数据对话(一):文档加载与切割使用langchain与你自己的数据对话(二):向量存储与嵌入使用langc…...

爬虫与搜索引擎优化:通过Python爬虫提升网站搜索排名
作为一名专业的爬虫程序员,我深知网站的搜索排名对于业务的重要性。在如今竞争激烈的网络世界中,如何让自己的网站在搜索引擎结果中脱颖而出,成为关键。今天,和大家分享一些关于如何通过Python爬虫来提升网站的搜索排名的技巧和实…...

2024软考系统架构设计师论文写作要点
一、写作注意事项 系统架构设计师的论文题目对于考生来说,是相对较难的题目。一方面,考生需要掌握论文题目中的系统架构设计的专业知识;另一方面,论文的撰写需要结合考生自身的项目经历。因此,如何将自己的项目经历和专业知识有机…...

【Maven】依赖范围、依赖传递、依赖排除、依赖原则、依赖继承
【Maven】依赖范围、依赖传递、依赖排除、依赖原则、依赖继承 依赖范围 依赖传递 依赖排除 依赖原则 依赖继承 依赖范围 在Maven中,依赖范围(Dependency Scope)用于控制依赖项在编译、测试和运行时的可见性和可用性。通过指定适当的依赖…...
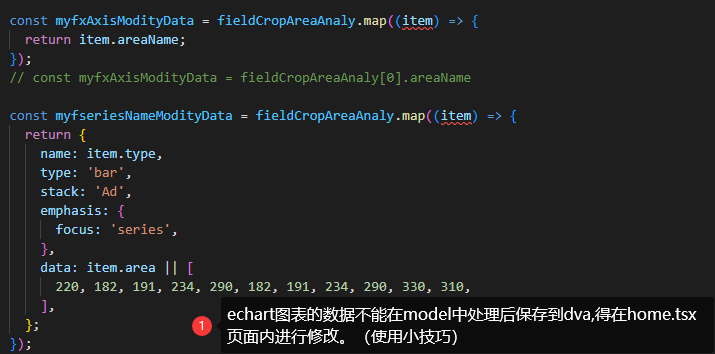
数组slice、splice字符串substr、split
一、定义 这篇文章主要对数组操作的两种方法进行介绍和使用,包括:slice、splice。对字符串操作的两种方法进行介绍和使用,包括:substr、split (一)、数组 slice:可以操作的数据类型有:数组字符串 splice:数组 操作数组…...

程序漏洞:安全威胁的隐患
在当今数字化时代,计算机程序是现代社会的核心基石。然而,随着技术的进步,程序漏洞也成为了一个不可忽视的问题。程序漏洞可能导致数据泄露、系统崩溃、恶意攻击和经济损失等一系列问题。本文将深入探讨程序漏洞的定义、分类、影响和预防措施…...

0基础学C#笔记09:希尔排序法
文章目录 前言一、希尔排序的思想二、使用步骤总结 前言 希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它…...

DOCKER的容器
1. 什么是Container(容器) 要有Container首先要有Image,也就是说Container是通过image创建的。 Container是在原先的Image之上新加的一层,称作Container layer,这一层是可读可写的(Image是只读的࿰…...
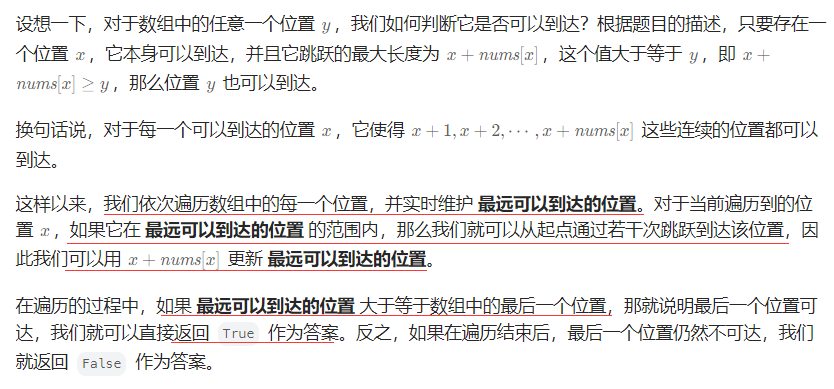
跳跃游戏——力扣55
文章目录 题目描述解法一 贪心题目描述 解法一 贪心 bool canJump(vector<int>& nums){int n=nums....
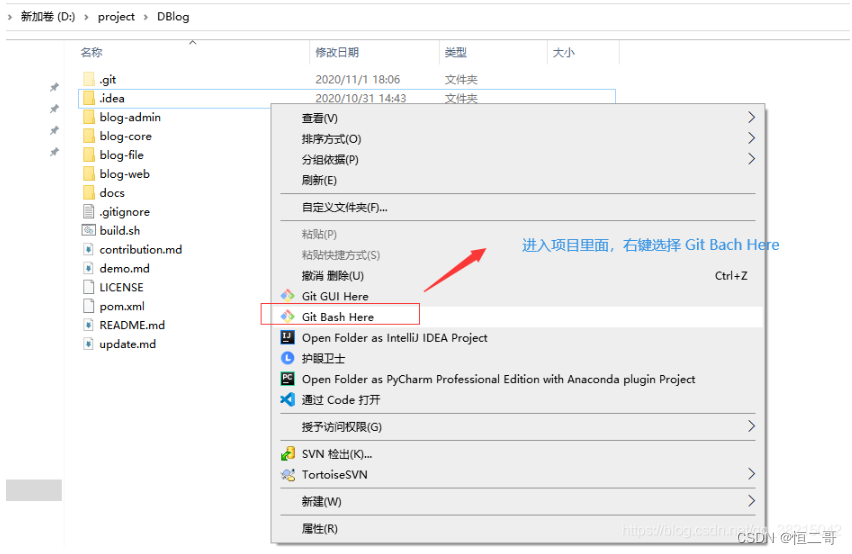
将本地项目上传至gitee的详细步骤
将本地项目上传至gitee的详细步骤 1.在gitee上创建以自己项目名称命名的空项目2.进入想上传的项目的文件夹,然后右键点击3. 初始化本地环境,把该项目变成可被git管理的仓库4.添加该项目下的所有文件5.使用如下命令将文件添加到仓库中去6.将本地代码库与远…...

iOS开发-导航栏UINavigationBar隐藏底部线及透明度
iOS 导航栏UINavigationBar隐藏底部线及透明度 苹果官方给出的解释: 如果你不调用方法设置一张背景图片的话,那就给你默认一张,然后同时还有一张阴影图片被默认设置上去,这就是导航栏上1px黑线的由来。 解决办法: 方…...

题目:2520.统计能整除数字的位数
题目来源: leetcode题目,网址:2520. 统计能整除数字的位数 - 力扣(LeetCode) 解题思路: 逐位判断即可。 解题代码: class Solution {public int countDigits(int num) {int res0;int ori…...
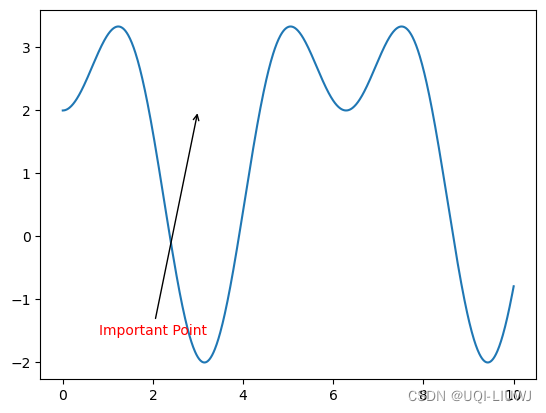
matplotlib 笔记 注释annotate
在图中的特定位置添加文本注释、箭头和连接线,以便更清晰地解释图形中的数据或信息 主要参数 text文本内容xy箭头指向的目标点的坐标xytext注释文本的坐标arrowprops 一个字典,指定注释箭头的属性,如颜色、箭头样式等 没有arrowprops的时候…...

Windows 无法安装到这个硬盘。选中的磁盘具有MBR分区。在EFI系统上,Windows只能安装到GPT磁盘
Windows无法安装到这个磁盘,选中的磁盘具有MBR分区表的解决方法 - 知乎 (zhihu.com) Windows无法安装到这个磁盘 选中的磁盘具有MBR分区表 - 知乎 (zhihu.com) 选中的磁盘具有MBR分区表,在EFI系统上,windows只能安装到GPT磁盘_选中的磁盘具有mbr分区表…...
学C的第三十三天【C语言文件操作】
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十二天【动态内存管理】_高高的胖子的博客-CSDN博客 1 . 为什么要使用文件 以前面写的通讯录为例,当通讯录运行起来的时候,可以给通讯录中增加、删…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
