scipy spatial transform Rotation库的源代码
前几日研究scipy的旋转,不知道具体里面怎么实现的,因此搜索一番。
发现Rotation在scipy的表达是用四元数的
https://github.com/jgagneastro/coffeegrindsize/edit/master/App/dist/coffeegrindsize.app/Contents/Resources/lib/python3.7/scipy/spatial/transform/rotation.py
from __future__ import division, print_function, absolute_import
import re
import warnings
import numpy as np
import scipy.linalg
from scipy._lib._util import check_random_state
_AXIS_TO_IND = {'x': 0, 'y': 1, 'z': 2}
def _elementary_basis_vector(axis):
b = np.zeros(3)
b[_AXIS_TO_IND[axis]] = 1
return b
def _compute_euler_from_dcm(dcm, seq, extrinsic=False):
# The algorithm assumes intrinsic frame transformations. For representation
# the paper uses transformation matrices, which are transpose of the
# direction cosine matrices used by our Rotation class.
# Adapt the algorithm for our case by
# 1. Instead of transposing our representation, use the transpose of the
# O matrix as defined in the paper, and be careful to swap indices
# 2. Reversing both axis sequence and angles for extrinsic rotations
if extrinsic:
seq = seq[::-1]
if dcm.ndim == 2:
dcm = dcm[None, :, :]
num_rotations = dcm.shape[0]
# Step 0
# Algorithm assumes axes as column vectors, here we use 1D vectors
n1 = _elementary_basis_vector(seq[0])
n2 = _elementary_basis_vector(seq[1])
n3 = _elementary_basis_vector(seq[2])
# Step 2
sl = np.dot(np.cross(n1, n2), n3)
cl = np.dot(n1, n3)
# angle offset is lambda from the paper referenced in [2] from docstring of
# `as_euler` function
offset = np.arctan2(sl, cl)
c = np.vstack((n2, np.cross(n1, n2), n1))
# Step 3
rot = np.array([
[1, 0, 0],
[0, cl, sl],
[0, -sl, cl],
])
res = np.einsum('...ij,...jk->...ik', c, dcm)
dcm_transformed = np.einsum('...ij,...jk->...ik', res, c.T.dot(rot))
# Step 4
angles = np.empty((num_rotations, 3))
# Ensure less than unit norm
positive_unity = dcm_transformed[:, 2, 2] > 1
negative_unity = dcm_transformed[:, 2, 2] < -1
dcm_transformed[positive_unity, 2, 2] = 1
dcm_transformed[negative_unity, 2, 2] = -1
angles[:, 1] = np.arccos(dcm_transformed[:, 2, 2])
# Steps 5, 6
eps = 1e-7
safe1 = (np.abs(angles[:, 1]) >= eps)
safe2 = (np.abs(angles[:, 1] - np.pi) >= eps)
# Step 4 (Completion)
angles[:, 1] += offset
# 5b
safe_mask = np.logical_and(safe1, safe2)
angles[safe_mask, 0] = np.arctan2(dcm_transformed[safe_mask, 0, 2],
-dcm_transformed[safe_mask, 1, 2])
angles[safe_mask, 2] = np.arctan2(dcm_transformed[safe_mask, 2, 0],
dcm_transformed[safe_mask, 2, 1])
if extrinsic:
# For extrinsic, set first angle to zero so that after reversal we
# ensure that third angle is zero
# 6a
angles[~safe_mask, 0] = 0
# 6b
angles[~safe1, 2] = np.arctan2(
dcm_transformed[~safe1, 1, 0] - dcm_transformed[~safe1, 0, 1],
dcm_transformed[~safe1, 0, 0] + dcm_transformed[~safe1, 1, 1]
)
# 6c
angles[~safe2, 2] = -np.arctan2(
dcm_transformed[~safe2, 1, 0] + dcm_transformed[~safe2, 0, 1],
dcm_transformed[~safe2, 0, 0] - dcm_transformed[~safe2, 1, 1]
)
else:
# For instrinsic, set third angle to zero
# 6a
angles[~safe_mask, 2] = 0
# 6b
angles[~safe1, 0] = np.arctan2(
dcm_transformed[~safe1, 1, 0] - dcm_transformed[~safe1, 0, 1],
dcm_transformed[~safe1, 0, 0] + dcm_transformed[~safe1, 1, 1]
)
# 6c
angles[~safe2, 0] = np.arctan2(
dcm_transformed[~safe2, 1, 0] + dcm_transformed[~safe2, 0, 1],
dcm_transformed[~safe2, 0, 0] - dcm_transformed[~safe2, 1, 1]
)
# Step 7
if seq[0] == seq[2]:
# lambda = 0, so we can only ensure angle2 -> [0, pi]
adjust_mask = np.logical_or(angles[:, 1] < 0, angles[:, 1] > np.pi)
else:
# lambda = + or - pi/2, so we can ensure angle2 -> [-pi/2, pi/2]
adjust_mask = np.logical_or(angles[:, 1] < -np.pi / 2,
angles[:, 1] > np.pi / 2)
# Dont adjust gimbal locked angle sequences
adjust_mask = np.logical_and(adjust_mask, safe_mask)
angles[adjust_mask, 0] += np.pi
angles[adjust_mask, 1] = 2 * offset - angles[adjust_mask, 1]
angles[adjust_mask, 2] -= np.pi
angles[angles < -np.pi] += 2 * np.pi
angles[angles > np.pi] -= 2 * np.pi
# Step 8
if not np.all(safe_mask):
warnings.warn("Gimbal lock detected. Setting third angle to zero since"
" it is not possible to uniquely determine all angles.")
# Reverse role of extrinsic and intrinsic rotations, but let third angle be
# zero for gimbal locked cases
if extrinsic:
angles = angles[:, ::-1]
return angles
def _make_elementary_quat(axis, angles):
quat = np.zeros((angles.shape[0], 4))
quat[:, 3] = np.cos(angles / 2)
quat[:, _AXIS_TO_IND[axis]] = np.sin(angles / 2)
return quat
def _compose_quat(p, q):
product = np.empty((max(p.shape[0], q.shape[0]), 4))
product[:, 3] = p[:, 3] * q[:, 3] - np.sum(p[:, :3] * q[:, :3], axis=1)
product[:, :3] = (p[:, None, 3] * q[:, :3] + q[:, None, 3] * p[:, :3] +
np.cross(p[:, :3], q[:, :3]))
return product
def _elementary_quat_compose(seq, angles, intrinsic=False):
result = _make_elementary_quat(seq[0], angles[:, 0])
for idx, axis in enumerate(seq[1:], start=1):
if intrinsic:
result = _compose_quat(
result,
_make_elementary_quat(axis, angles[:, idx]))
else:
result = _compose_quat(
_make_elementary_quat(axis, angles[:, idx]),
result)
return result
class Rotation(object):
"""Rotation in 3 dimensions.
This class provides an interface to initialize from and represent rotations
with:
- Quaternions
- Direction Cosine Matrices
- Rotation Vectors
- Euler angles
The following operations on rotations are supported:
- Application on vectors
- Rotation Composition
- Rotation Inversion
- Rotation Indexing
Indexing within a rotation is supported since multiple rotation transforms
can be stored within a single `Rotation` instance.
To create `Rotation` objects use ``from_...`` methods (see examples below).
``Rotation(...)`` is not supposed to be instantiated directly.
Methods
-------
__len__
from_quat
from_dcm
from_rotvec
from_euler
as_quat
as_dcm
as_rotvec
as_euler
apply
__mul__
inv
__getitem__
random
match_vectors
See Also
--------
Slerp
Notes
-----
.. versionadded: 1.2.0
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
A `Rotation` instance can be initialized in any of the above formats and
converted to any of the others. The underlying object is independent of the
representation used for initialization.
Consider a counter-clockwise rotation of 90 degrees about the z-axis. This
corresponds to the following quaternion (in scalar-last format):
>>> r = R.from_quat([0, 0, np.sin(np.pi/4), np.cos(np.pi/4)])
The rotation can be expressed in any of the other formats:
>>> r.as_dcm()
array([[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
>>> r.as_rotvec()
array([0. , 0. , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90., 0., 0.])
The same rotation can be initialized using a direction cosine matrix:
>>> r = R.from_dcm(np.array([
... [0, -1, 0],
... [1, 0, 0],
... [0, 0, 1]]))
Representation in other formats:
>>> r.as_quat()
array([0. , 0. , 0.70710678, 0.70710678])
>>> r.as_rotvec()
array([0. , 0. , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90., 0., 0.])
The rotation vector corresponding to this rotation is given by:
>>> r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))
Representation in other formats:
>>> r.as_quat()
array([0. , 0. , 0.70710678, 0.70710678])
>>> r.as_dcm()
array([[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
>>> r.as_euler('zyx', degrees=True)
array([90., 0., 0.])
The ``from_euler`` method is quite flexible in the range of input formats
it supports. Here we initialize a single rotation about a single axis:
>>> r = R.from_euler('z', 90, degrees=True)
Again, the object is representation independent and can be converted to any
other format:
>>> r.as_quat()
array([0. , 0. , 0.70710678, 0.70710678])
>>> r.as_dcm()
array([[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
>>> r.as_rotvec()
array([0. , 0. , 1.57079633])
It is also possible to initialize multiple rotations in a single instance
using any of the `from_...` functions. Here we initialize a stack of 3
rotations using the ``from_euler`` method:
>>> r = R.from_euler('zyx', [
... [90, 0, 0],
... [0, 45, 0],
... [45, 60, 30]], degrees=True)
The other representations also now return a stack of 3 rotations. For
example:
>>> r.as_quat()
array([[0. , 0. , 0.70710678, 0.70710678],
[0. , 0.38268343, 0. , 0.92387953],
[0.39190384, 0.36042341, 0.43967974, 0.72331741]])
Applying the above rotations onto a vector:
>>> v = [1, 2, 3]
>>> r.apply(v)
array([[-2. , 1. , 3. ],
[ 2.82842712, 2. , 1.41421356],
[ 2.24452282, 0.78093109, 2.89002836]])
A `Rotation` instance can be indexed and sliced as if it were a single
1D array or list:
>>> r.as_quat()
array([[0. , 0. , 0.70710678, 0.70710678],
[0. , 0.38268343, 0. , 0.92387953],
[0.39190384, 0.36042341, 0.43967974, 0.72331741]])
>>> p = r[0]
>>> p.as_dcm()
array([[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
>>> q = r[1:3]
>>> q.as_quat()
array([[0. , 0.38268343, 0. , 0.92387953],
[0.39190384, 0.36042341, 0.43967974, 0.72331741]])
Multiple rotations can be composed using the ``*`` operator:
>>> r1 = R.from_euler('z', 90, degrees=True)
>>> r2 = R.from_rotvec([np.pi/4, 0, 0])
>>> v = [1, 2, 3]
>>> r2.apply(r1.apply(v))
array([-2. , -1.41421356, 2.82842712])
>>> r3 = r2 * r1 # Note the order
>>> r3.apply(v)
array([-2. , -1.41421356, 2.82842712])
Finally, it is also possible to invert rotations:
>>> r1 = R.from_euler('z', [90, 45], degrees=True)
>>> r2 = r1.inv()
>>> r2.as_euler('zyx', degrees=True)
array([[-90., 0., 0.],
[-45., 0., 0.]])
These examples serve as an overview into the `Rotation` class and highlight
major functionalities. For more thorough examples of the range of input and
output formats supported, consult the individual method's examples.
"""
def __init__(self, quat, normalized=False, copy=True):
self._single = False
quat = np.asarray(quat, dtype=float)
if quat.ndim not in [1, 2] or quat.shape[-1] != 4:
raise ValueError("Expected `quat` to have shape (4,) or (N x 4), "
"got {}.".format(quat.shape))
# If a single quaternion is given, convert it to a 2D 1 x 4 matrix but
# set self._single to True so that we can return appropriate objects
# in the `to_...` methods
if quat.shape == (4,):
quat = quat[None, :]
self._single = True
if normalized:
self._quat = quat.copy() if copy else quat
else:
self._quat = quat.copy()
norms = scipy.linalg.norm(quat, axis=1)
zero_norms = norms == 0
if zero_norms.any():
raise ValueError("Found zero norm quaternions in `quat`.")
# Ensure norm is broadcasted along each column.
self._quat[~zero_norms] /= norms[~zero_norms][:, None]
def __len__(self):
"""Number of rotations contained in this object.
Multiple rotations can be stored in a single instance.
Returns
-------
length : int
Number of rotations stored in object.
"""
return self._quat.shape[0]
@classmethod
def from_quat(cls, quat, normalized=False):
"""Initialize from quaternions.
3D rotations can be represented using unit-norm quaternions [1]_.
Parameters
----------
quat : array_like, shape (N, 4) or (4,)
Each row is a (possibly non-unit norm) quaternion in scalar-last
(x, y, z, w) format.
normalized : bool, optional
If False, input quaternions are normalized to unit norm before
being stored. If True, quaternions are assumed to already have
unit norm and are stored as given. Default is False.
Returns
-------
rotation : `Rotation` instance
Object containing the rotations represented by input quaternions.
References
----------
.. [1] https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Initialize a single rotation:
>>> r = R.from_quat([1, 0, 0, 0])
>>> r.as_quat()
array([1., 0., 0., 0.])
>>> r.as_quat().shape
(4,)
Initialize multiple rotations in a single object:
>>> r = R.from_quat([
... [1, 0, 0, 0],
... [0, 0, 0, 1]
... ])
>>> r.as_quat()
array([[1., 0., 0., 0.],
[0., 0., 0., 1.]])
>>> r.as_quat().shape
(2, 4)
It is also possible to have a stack of a single rotation:
>>> r = R.from_quat([[0, 0, 0, 1]])
>>> r.as_quat()
array([[0., 0., 0., 1.]])
>>> r.as_quat().shape
(1, 4)
By default, quaternions are normalized before initialization.
>>> r = R.from_quat([0, 0, 1, 1])
>>> r.as_quat()
array([0. , 0. , 0.70710678, 0.70710678])
If unit norms are ensured, skip the normalization step.
>>> r = R.from_quat([0, 0, 1, 0], normalized=True)
>>> r.as_quat()
array([0., 0., 1., 0.])
"""
return cls(quat, normalized)
@classmethod
def from_dcm(cls, dcm):
"""Initialize from direction cosine matrices.
Rotations in 3 dimensions can be represented using 3 x 3 proper
orthogonal matrices [1]_. If the input is not proper orthogonal,
an approximation is created using the method described in [2]_.
Parameters
----------
dcm : array_like, shape (N, 3, 3) or (3, 3)
A single matrix or a stack of matrices, where ``dcm[i]`` is the i-th
matrix.
Returns
-------
rotation : `Rotation` instance
Object containing the rotations represented by the input direction
cosine matrices.
References
----------
.. [1] https://en.wikipedia.org/wiki/Rotation_matrix#In_three_dimensions
.. [2] F. Landis Markley, "Unit Quaternion from Rotation Matrix",
Journal of guidance, control, and dynamics vol. 31.2, pp.
440-442, 2008.
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Initialize a single rotation:
>>> r = R.from_dcm([
... [0, -1, 0],
... [1, 0, 0],
... [0, 0, 1]])
>>> r.as_dcm().shape
(3, 3)
Initialize multiple rotations in a single object:
>>> r = R.from_dcm([
... [
... [0, -1, 0],
... [1, 0, 0],
... [0, 0, 1],
... ],
... [
... [1, 0, 0],
... [0, 0, -1],
... [0, 1, 0],
... ]])
>>> r.as_dcm().shape
(2, 3, 3)
If input matrices are not special orthogonal (orthogonal with
determinant equal to +1), then a special orthogonal estimate is stored:
>>> a = np.array([
... [0, -0.5, 0],
... [0.5, 0, 0],
... [0, 0, 0.5]])
>>> np.linalg.det(a)
0.12500000000000003
>>> r = R.from_dcm(a)
>>> dcm = r.as_dcm()
>>> dcm
array([[-0.38461538, -0.92307692, 0. ],
[ 0.92307692, -0.38461538, 0. ],
[ 0. , 0. , 1. ]])
>>> np.linalg.det(dcm)
1.0000000000000002
It is also possible to have a stack containing a single rotation:
>>> r = R.from_dcm([[
... [0, -1, 0],
... [1, 0, 0],
... [0, 0, 1]]])
>>> r.as_dcm()
array([[[ 0., -1., 0.],
[ 1., 0., 0.],
[ 0., 0., 1.]]])
>>> r.as_dcm().shape
(1, 3, 3)
"""
is_single = False
dcm = np.asarray(dcm, dtype=float)
if dcm.ndim not in [2, 3] or dcm.shape[-2:] != (3, 3):
raise ValueError("Expected `dcm` to have shape (3, 3) or "
"(N, 3, 3), got {}".format(dcm.shape))
# If a single dcm is given, convert it to 3D 1 x 3 x 3 matrix but set
# self._single to True so that we can return appropriate objects in
# the `to_...` methods
if dcm.shape == (3, 3):
dcm = dcm.reshape((1, 3, 3))
is_single = True
num_rotations = dcm.shape[0]
decision_matrix = np.empty((num_rotations, 4))
decision_matrix[:, :3] = dcm.diagonal(axis1=1, axis2=2)
decision_matrix[:, -1] = decision_matrix[:, :3].sum(axis=1)
choices = decision_matrix.argmax(axis=1)
quat = np.empty((num_rotations, 4))
ind = np.nonzero(choices != 3)[0]
i = choices[ind]
j = (i + 1) % 3
k = (j + 1) % 3
quat[ind, i] = 1 - decision_matrix[ind, -1] + 2 * dcm[ind, i, i]
quat[ind, j] = dcm[ind, j, i] + dcm[ind, i, j]
quat[ind, k] = dcm[ind, k, i] + dcm[ind, i, k]
quat[ind, 3] = dcm[ind, k, j] - dcm[ind, j, k]
ind = np.nonzero(choices == 3)[0]
quat[ind, 0] = dcm[ind, 2, 1] - dcm[ind, 1, 2]
quat[ind, 1] = dcm[ind, 0, 2] - dcm[ind, 2, 0]
quat[ind, 2] = dcm[ind, 1, 0] - dcm[ind, 0, 1]
quat[ind, 3] = 1 + decision_matrix[ind, -1]
quat /= np.linalg.norm(quat, axis=1)[:, None]
if is_single:
return cls(quat[0], normalized=True, copy=False)
else:
return cls(quat, normalized=True, copy=False)
@classmethod
def from_rotvec(cls, rotvec):
"""Initialize from rotation vectors.
A rotation vector is a 3 dimensional vector which is co-directional to
the axis of rotation and whose norm gives the angle of rotation (in
radians) [1]_.
Parameters
----------
rotvec : array_like, shape (N, 3) or (3,)
A single vector or a stack of vectors, where `rot_vec[i]` gives
the ith rotation vector.
Returns
-------
rotation : `Rotation` instance
Object containing the rotations represented by input rotation
vectors.
References
----------
.. [1] https://en.wikipedia.org/wiki/Axis%E2%80%93angle_representation#Rotation_vector
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Initialize a single rotation:
>>> r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))
>>> r.as_rotvec()
array([0. , 0. , 1.57079633])
>>> r.as_rotvec().shape
(3,)
Initialize multiple rotations in one object:
>>> r = R.from_rotvec([
... [0, 0, np.pi/2],
... [np.pi/2, 0, 0]])
>>> r.as_rotvec()
array([[0. , 0. , 1.57079633],
[1.57079633, 0. , 0. ]])
>>> r.as_rotvec().shape
(2, 3)
It is also possible to have a stack of a single rotaton:
>>> r = R.from_rotvec([[0, 0, np.pi/2]])
>>> r.as_rotvec().shape
(1, 3)
"""
is_single = False
rotvec = np.asarray(rotvec, dtype=float)
if rotvec.ndim not in [1, 2] or rotvec.shape[-1] != 3:
raise ValueError("Expected `rot_vec` to have shape (3,) "
"or (N, 3), got {}".format(rotvec.shape))
# If a single vector is given, convert it to a 2D 1 x 3 matrix but
# set self._single to True so that we can return appropriate objects
# in the `as_...` methods
if rotvec.shape == (3,):
rotvec = rotvec[None, :]
is_single = True
num_rotations = rotvec.shape[0]
norms = np.linalg.norm(rotvec, axis=1)
small_angle = (norms <= 1e-3)
large_angle = ~small_angle
scale = np.empty(num_rotations)
scale[small_angle] = (0.5 - norms[small_angle] ** 2 / 48 +
norms[small_angle] ** 4 / 3840)
scale[large_angle] = (np.sin(norms[large_angle] / 2) /
norms[large_angle])
quat = np.empty((num_rotations, 4))
quat[:, :3] = scale[:, None] * rotvec
quat[:, 3] = np.cos(norms / 2)
if is_single:
return cls(quat[0], normalized=True, copy=False)
else:
return cls(quat, normalized=True, copy=False)
@classmethod
def from_euler(cls, seq, angles, degrees=False):
"""Initialize from Euler angles.
Rotations in 3 dimensions can be represented by a sequece of 3
rotations around a sequence of axes. In theory, any three axes spanning
the 3D Euclidean space are enough. In practice the axes of rotation are
chosen to be the basis vectors.
The three rotations can either be in a global frame of reference
(extrinsic) or in a body centred frame of refernce (intrinsic), which
is attached to, and moves with, the object under rotation [1]_.
Parameters
----------
seq : string
Specifies sequence of axes for rotations. Up to 3 characters
belonging to the set {'X', 'Y', 'Z'} for intrinsic rotations, or
{'x', 'y', 'z'} for extrinsic rotations. Extrinsic and intrinsic
rotations cannot be mixed in one function call.
angles : float or array_like, shape (N,) or (N, [1 or 2 or 3])
Euler angles specified in radians (`degrees` is False) or degrees
(`degrees` is True).
For a single character `seq`, `angles` can be:
- a single value
- array_like with shape (N,), where each `angle[i]`
corresponds to a single rotation
- array_like with shape (N, 1), where each `angle[i, 0]`
corresponds to a single rotation
For 2- and 3-character wide `seq`, `angles` can be:
- array_like with shape (W,) where `W` is the width of
`seq`, which corresponds to a single rotation with `W` axes
- array_like with shape (N, W) where each `angle[i]`
corresponds to a sequence of Euler angles describing a single
rotation
degrees : bool, optional
If True, then the given angles are assumed to be in degrees.
Default is False.
Returns
-------
rotation : `Rotation` instance
Object containing the rotation represented by the sequence of
rotations around given axes with given angles.
References
----------
.. [1] https://en.wikipedia.org/wiki/Euler_angles#Definition_by_intrinsic_rotations
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Initialize a single rotation along a single axis:
>>> r = R.from_euler('x', 90, degrees=True)
>>> r.as_quat().shape
(4,)
Initialize a single rotation with a given axis sequence:
>>> r = R.from_euler('zyx', [90, 45, 30], degrees=True)
>>> r.as_quat().shape
(4,)
Initialize a stack with a single rotation around a single axis:
>>> r = R.from_euler('x', [90], degrees=True)
>>> r.as_quat().shape
(1, 4)
Initialize a stack with a single rotation with an axis sequence:
>>> r = R.from_euler('zyx', [[90, 45, 30]], degrees=True)
>>> r.as_quat().shape
(1, 4)
Initialize multiple elementary rotations in one object:
>>> r = R.from_euler('x', [90, 45, 30], degrees=True)
>>> r.as_quat().shape
(3, 4)
Initialize multiple rotations in one object:
>>> r = R.from_euler('zyx', [[90, 45, 30], [35, 45, 90]], degrees=True)
>>> r.as_quat().shape
(2, 4)
"""
num_axes = len(seq)
if num_axes < 1 or num_axes > 3:
raise ValueError("Expected axis specification to be a non-empty "
"string of upto 3 characters, got {}".format(seq))
intrinsic = (re.match(r'^[XYZ]{1,3}$', seq) is not None)
extrinsic = (re.match(r'^[xyz]{1,3}$', seq) is not None)
if not (intrinsic or extrinsic):
raise ValueError("Expected axes from `seq` to be from ['x', 'y', "
"'z'] or ['X', 'Y', 'Z'], got {}".format(seq))
if any(seq[i] == seq[i+1] for i in range(num_axes - 1)):
raise ValueError("Expected consecutive axes to be different, "
"got {}".format(seq))
seq = seq.lower()
angles = np.asarray(angles, dtype=float)
if degrees:
angles = np.deg2rad(angles)
is_single = False
# Prepare angles to have shape (num_rot, num_axes)
if num_axes == 1:
if angles.ndim == 0:
# (1, 1)
angles = angles.reshape((1, 1))
is_single = True
elif angles.ndim == 1:
# (N, 1)
angles = angles[:, None]
elif angles.ndim == 2 and angles.shape[-1] != 1:
raise ValueError("Expected `angles` parameter to have shape "
"(N, 1), got {}.".format(angles.shape))
elif angles.ndim > 2:
raise ValueError("Expected float, 1D array, or 2D array for "
"parameter `angles` corresponding to `seq`, "
"got shape {}.".format(angles.shape))
else: # 2 or 3 axes
if angles.ndim not in [1, 2] or angles.shape[-1] != num_axes:
raise ValueError("Expected `angles` to be at most "
"2-dimensional with width equal to number "
"of axes specified, got {} for shape".format(
angles.shape))
if angles.ndim == 1:
# (1, num_axes)
angles = angles[None, :]
is_single = True
# By now angles should have shape (num_rot, num_axes)
# sanity check
if angles.ndim != 2 or angles.shape[-1] != num_axes:
raise ValueError("Expected angles to have shape (num_rotations, "
"num_axes), got {}.".format(angles.shape))
quat = _elementary_quat_compose(seq, angles, intrinsic)
return cls(quat[0] if is_single else quat, normalized=True, copy=False)
def as_quat(self):
"""Represent as quaternions.
Rotations in 3 dimensions can be represented using unit norm
quaternions [1]_. The mapping from quaternions to rotations is
two-to-one, i.e. quaternions ``q`` and ``-q``, where ``-q`` simply
reverses the sign of each component, represent the same spatial
rotation.
Returns
-------
quat : `numpy.ndarray`, shape (4,) or (N, 4)
Shape depends on shape of inputs used for initialization.
References
----------
.. [1] https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Represent a single rotation:
>>> r = R.from_dcm([
... [0, -1, 0],
... [1, 0, 0],
... [0, 0, 1]])
>>> r.as_quat()
array([0. , 0. , 0.70710678, 0.70710678])
>>> r.as_quat().shape
(4,)
Represent a stack with a single rotation:
>>> r = R.from_quat([[0, 0, 0, 1]])
>>> r.as_quat().shape
(1, 4)
Represent multiple rotaions in a single object:
>>> r = R.from_rotvec([[np.pi, 0, 0], [0, 0, np.pi/2]])
>>> r.as_quat().shape
(2, 4)
"""
if self._single:
return self._quat[0].copy()
else:
return self._quat.copy()
def as_dcm(self):
"""Represent as direction cosine matrices.
3D rotations can be represented using direction cosine matrices, which
are 3 x 3 real orthogonal matrices with determinant equal to +1 [1]_.
Returns
-------
dcm : ndarray, shape (3, 3) or (N, 3, 3)
Shape depends on shape of inputs used for initialization.
References
----------
.. [1] https://en.wikipedia.org/wiki/Rotation_matrix#In_three_dimensions
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Represent a single rotation:
>>> r = R.from_rotvec([0, 0, np.pi/2])
>>> r.as_dcm()
array([[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
>>> r.as_dcm().shape
(3, 3)
Represent a stack with a single rotation:
>>> r = R.from_quat([[1, 1, 0, 0]])
>>> r.as_dcm()
array([[[ 0., 1., 0.],
[ 1., 0., 0.],
[ 0., 0., -1.]]])
>>> r.as_dcm().shape
(1, 3, 3)
Represent multiple rotations:
>>> r = R.from_rotvec([[np.pi/2, 0, 0], [0, 0, np.pi/2]])
>>> r.as_dcm()
array([[[ 1.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[ 0.00000000e+00, 2.22044605e-16, -1.00000000e+00],
[ 0.00000000e+00, 1.00000000e+00, 2.22044605e-16]],
[[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]]])
>>> r.as_dcm().shape
(2, 3, 3)
"""
x = self._quat[:, 0]
y = self._quat[:, 1]
z = self._quat[:, 2]
w = self._quat[:, 3]
x2 = x * x
y2 = y * y
z2 = z * z
w2 = w * w
xy = x * y
zw = z * w
xz = x * z
yw = y * w
yz = y * z
xw = x * w
num_rotations = len(self)
dcm = np.empty((num_rotations, 3, 3))
dcm[:, 0, 0] = x2 - y2 - z2 + w2
dcm[:, 1, 0] = 2 * (xy + zw)
dcm[:, 2, 0] = 2 * (xz - yw)
dcm[:, 0, 1] = 2 * (xy - zw)
dcm[:, 1, 1] = - x2 + y2 - z2 + w2
dcm[:, 2, 1] = 2 * (yz + xw)
dcm[:, 0, 2] = 2 * (xz + yw)
dcm[:, 1, 2] = 2 * (yz - xw)
dcm[:, 2, 2] = - x2 - y2 + z2 + w2
if self._single:
return dcm[0]
else:
return dcm
def as_rotvec(self):
"""Represent as rotation vectors.
A rotation vector is a 3 dimensional vector which is co-directional to
the axis of rotation and whose norm gives the angle of rotation (in
radians) [1]_.
Returns
-------
rotvec : ndarray, shape (3,) or (N, 3)
Shape depends on shape of inputs used for initialization.
References
----------
.. [1] https://en.wikipedia.org/wiki/Axis%E2%80%93angle_representation#Rotation_vector
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Represent a single rotation:
>>> r = R.from_euler('z', 90, degrees=True)
>>> r.as_rotvec()
array([0. , 0. , 1.57079633])
>>> r.as_rotvec().shape
(3,)
Represent a stack with a single rotation:
>>> r = R.from_quat([[0, 0, 1, 1]])
>>> r.as_rotvec()
array([[0. , 0. , 1.57079633]])
>>> r.as_rotvec().shape
(1, 3)
Represent multiple rotations in a single object:
>>> r = R.from_quat([[0, 0, 1, 1], [1, 1, 0, 1]])
>>> r.as_rotvec()
array([[0. , 0. , 1.57079633],
[1.35102172, 1.35102172, 0. ]])
>>> r.as_rotvec().shape
(2, 3)
"""
quat = self._quat.copy()
# w > 0 to ensure 0 <= angle <= pi
quat[quat[:, 3] < 0] *= -1
angle = 2 * np.arctan2(np.linalg.norm(quat[:, :3], axis=1), quat[:, 3])
small_angle = (angle <= 1e-3)
large_angle = ~small_angle
num_rotations = len(self)
scale = np.empty(num_rotations)
scale[small_angle] = (2 + angle[small_angle] ** 2 / 12 +
7 * angle[small_angle] ** 4 / 2880)
scale[large_angle] = (angle[large_angle] /
np.sin(angle[large_angle] / 2))
rotvec = scale[:, None] * quat[:, :3]
if self._single:
return rotvec[0]
else:
return rotvec
def as_euler(self, seq, degrees=False):
"""Represent as Euler angles.
Any orientation can be expressed as a composition of 3 elementary
rotations. Once the axis sequence has been chosen, Euler angles define
the angle of rotation around each respective axis [1]_.
The algorithm from [2]_ has been used to calculate Euler angles for the
rotation about a given sequence of axes.
Euler angles suffer from the problem of gimbal lock [3]_, where the
representation loses a degree of freedom and it is not possible to
determine the first and third angles uniquely. In this case,
a warning is raised, and the third angle is set to zero. Note however
that the returned angles still represent the correct rotation.
Parameters
----------
seq : string, length 3
3 characters belonging to the set {'X', 'Y', 'Z'} for intrinsic
rotations, or {'x', 'y', 'z'} for extrinsic rotations [1]_.
Adjacent axes cannot be the same.
Extrinsic and intrinsic rotations cannot be mixed in one function
call.
degrees : boolean, optional
Returned angles are in degrees if this flag is True, else they are
in radians. Default is False.
Returns
-------
angles : ndarray, shape (3,) or (N, 3)
Shape depends on shape of inputs used to initialize object.
The returned angles are in the range:
- First angle belongs to [-180, 180] degrees (both inclusive)
- Third angle belongs to [-180, 180] degrees (both inclusive)
- Second angle belongs to:
- [-90, 90] degrees if all axes are different (like xyz)
- [0, 180] degrees if first and third axes are the same
(like zxz)
References
----------
.. [1] https://en.wikipedia.org/wiki/Euler_angles#Definition_by_intrinsic_rotations
.. [2] Malcolm D. Shuster, F. Landis Markley, "General formula for
extraction the Euler angles", Journal of guidance, control, and
dynamics, vol. 29.1, pp. 215-221. 2006
.. [3] https://en.wikipedia.org/wiki/Gimbal_lock#In_applied_mathematics
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Represent a single rotation:
>>> r = R.from_rotvec([0, 0, np.pi/2])
>>> r.as_euler('zxy', degrees=True)
array([90., 0., 0.])
>>> r.as_euler('zxy', degrees=True).shape
(3,)
Represent a stack of single rotation:
>>> r = R.from_rotvec([[0, 0, np.pi/2]])
>>> r.as_euler('zxy', degrees=True)
array([[90., 0., 0.]])
>>> r.as_euler('zxy', degrees=True).shape
(1, 3)
Represent multiple rotations in a single object:
>>> r = R.from_rotvec([
... [0, 0, np.pi/2],
... [0, -np.pi/3, 0],
... [np.pi/4, 0, 0]])
>>> r.as_euler('zxy', degrees=True)
array([[ 90., 0., 0.],
[ 0., 0., -60.],
[ 0., 45., 0.]])
>>> r.as_euler('zxy', degrees=True).shape
(3, 3)
"""
if len(seq) != 3:
raise ValueError("Expected 3 axes, got {}.".format(seq))
intrinsic = (re.match(r'^[XYZ]{1,3}$', seq) is not None)
extrinsic = (re.match(r'^[xyz]{1,3}$', seq) is not None)
if not (intrinsic or extrinsic):
raise ValueError("Expected axes from `seq` to be from "
"['x', 'y', 'z'] or ['X', 'Y', 'Z'], "
"got {}".format(seq))
if any(seq[i] == seq[i+1] for i in range(2)):
raise ValueError("Expected consecutive axes to be different, "
"got {}".format(seq))
seq = seq.lower()
angles = _compute_euler_from_dcm(self.as_dcm(), seq, extrinsic)
if degrees:
angles = np.rad2deg(angles)
return angles[0] if self._single else angles
def apply(self, vectors, inverse=False):
"""Apply this rotation to a set of vectors.
If the original frame rotates to the final frame by this rotation, then
its application to a vector can be seen in two ways:
- As a projection of vector components expressed in the final frame
to the original frame.
- As the physical rotation of a vector being glued to the original
frame as it rotates. In this case the vector components are
expressed in the original frame before and after the rotation.
In terms of DCMs, this application is the same as
``self.as_dcm().dot(vectors)``.
Parameters
----------
vectors : array_like, shape (3,) or (N, 3)
Each `vectors[i]` represents a vector in 3D space. A single vector
can either be specified with shape `(3, )` or `(1, 3)`. The number
of rotations and number of vectors given must follow standard numpy
broadcasting rules: either one of them equals unity or they both
equal each other.
inverse : boolean, optional
If True then the inverse of the rotation(s) is applied to the input
vectors. Default is False.
Returns
-------
rotated_vectors : ndarray, shape (3,) or (N, 3)
Result of applying rotation on input vectors.
Shape depends on the following cases:
- If object contains a single rotation (as opposed to a stack
with a single rotation) and a single vector is specified with
shape ``(3,)``, then `rotated_vectors` has shape ``(3,)``.
- In all other cases, `rotated_vectors` has shape ``(N, 3)``,
where ``N`` is either the number of rotations or vectors.
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Single rotation applied on a single vector:
>>> vector = np.array([1, 0, 0])
>>> r = R.from_rotvec([0, 0, np.pi/2])
>>> r.as_dcm()
array([[ 2.22044605e-16, -1.00000000e+00, 0.00000000e+00],
[ 1.00000000e+00, 2.22044605e-16, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]])
>>> r.apply(vector)
array([2.22044605e-16, 1.00000000e+00, 0.00000000e+00])
>>> r.apply(vector).shape
(3,)
Single rotation applied on multiple vectors:
>>> vectors = np.array([
... [1, 0, 0],
... [1, 2, 3]])
>>> r = R.from_rotvec([0, 0, np.pi/4])
>>> r.as_dcm()
array([[ 0.70710678, -0.70710678, 0. ],
[ 0.70710678, 0.70710678, 0. ],
[ 0. , 0. , 1. ]])
>>> r.apply(vectors)
array([[ 0.70710678, 0.70710678, 0. ],
[-0.70710678, 2.12132034, 3. ]])
>>> r.apply(vectors).shape
(2, 3)
Multiple rotations on a single vector:
>>> r = R.from_rotvec([[0, 0, np.pi/4], [np.pi/2, 0, 0]])
>>> vector = np.array([1,2,3])
>>> r.as_dcm()
array([[[ 7.07106781e-01, -7.07106781e-01, 0.00000000e+00],
[ 7.07106781e-01, 7.07106781e-01, 0.00000000e+00],
[ 0.00000000e+00, 0.00000000e+00, 1.00000000e+00]],
[[ 1.00000000e+00, 0.00000000e+00, 0.00000000e+00],
[ 0.00000000e+00, 2.22044605e-16, -1.00000000e+00],
[ 0.00000000e+00, 1.00000000e+00, 2.22044605e-16]]])
>>> r.apply(vector)
array([[-0.70710678, 2.12132034, 3. ],
[ 1. , -3. , 2. ]])
>>> r.apply(vector).shape
(2, 3)
Multiple rotations on multiple vectors. Each rotation is applied on the
corresponding vector:
>>> r = R.from_euler('zxy', [
... [0, 0, 90],
... [45, 30, 60]], degrees=True)
>>> vectors = [
... [1, 2, 3],
... [1, 0, -1]]
>>> r.apply(vectors)
array([[ 3. , 2. , -1. ],
[-0.09026039, 1.11237244, -0.86860844]])
>>> r.apply(vectors).shape
(2, 3)
It is also possible to apply the inverse rotation:
>>> r = R.from_euler('zxy', [
... [0, 0, 90],
... [45, 30, 60]], degrees=True)
>>> vectors = [
... [1, 2, 3],
... [1, 0, -1]]
>>> r.apply(vectors, inverse=True)
array([[-3. , 2. , 1. ],
[ 1.09533535, -0.8365163 , 0.3169873 ]])
"""
vectors = np.asarray(vectors)
if vectors.ndim > 2 or vectors.shape[-1] != 3:
raise ValueError("Expected input of shape (3,) or (P, 3), "
"got {}.".format(vectors.shape))
single_vector = False
if vectors.shape == (3,):
single_vector = True
vectors = vectors[None, :]
dcm = self.as_dcm()
if self._single:
dcm = dcm[None, :, :]
n_vectors = vectors.shape[0]
n_rotations = len(self)
if n_vectors != 1 and n_rotations != 1 and n_vectors != n_rotations:
raise ValueError("Expected equal numbers of rotations and vectors "
", or a single rotation, or a single vector, got "
"{} rotations and {} vectors.".format(
n_rotations, n_vectors))
if inverse:
result = np.einsum('ikj,ik->ij', dcm, vectors)
else:
result = np.einsum('ijk,ik->ij', dcm, vectors)
if self._single and single_vector:
return result[0]
else:
return result
def __mul__(self, other):
"""Compose this rotation with the other.
If `p` and `q` are two rotations, then the composition of 'q followed
by p' is equivalent to `p * q`. In terms of DCMs, the composition can
be expressed as `p.as_dcm().dot(q.as_dcm())`.
Parameters
----------
other : `Rotation` instance
Object containing the rotaions to be composed with this one. Note
that rotation compositions are not commutative, so ``p * q`` is
different from ``q * p``.
Returns
-------
composition : `Rotation` instance
This function supports composition of multiple rotations at a time.
The following cases are possible:
- Either ``p`` or ``q`` contains a single rotation. In this case
`composition` contains the result of composing each rotation in
the other object with the single rotation.
- Both ``p`` and ``q`` contain ``N`` rotations. In this case each
rotation ``p[i]`` is composed with the corresponding rotation
``q[i]`` and `output` contains ``N`` rotations.
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Composition of two single rotations:
>>> p = R.from_quat([0, 0, 1, 1])
>>> q = R.from_quat([1, 0, 0, 1])
>>> p.as_dcm()
array([[ 0., -1., 0.],
[ 1., 0., 0.],
[ 0., 0., 1.]])
>>> q.as_dcm()
array([[ 1., 0., 0.],
[ 0., 0., -1.],
[ 0., 1., 0.]])
>>> r = p * q
>>> r.as_dcm()
array([[0., 0., 1.],
[1., 0., 0.],
[0., 1., 0.]])
Composition of two objects containing equal number of rotations:
>>> p = R.from_quat([[0, 0, 1, 1], [1, 0, 0, 1]])
>>> q = R.from_rotvec([[np.pi/4, 0, 0], [-np.pi/4, 0, np.pi/4]])
>>> p.as_quat()
array([[0. , 0. , 0.70710678, 0.70710678],
[0.70710678, 0. , 0. , 0.70710678]])
>>> q.as_quat()
array([[ 0.38268343, 0. , 0. , 0.92387953],
[-0.37282173, 0. , 0.37282173, 0.84971049]])
>>> r = p * q
>>> r.as_quat()
array([[ 0.27059805, 0.27059805, 0.65328148, 0.65328148],
[ 0.33721128, -0.26362477, 0.26362477, 0.86446082]])
"""
if not(len(self) == 1 or len(other) == 1 or len(self) == len(other)):
raise ValueError("Expected equal number of rotations in both "
"or a single rotation in either object, "
"got {} rotations in first and {} rotations in "
"second object.".format(
len(self), len(other)))
result = _compose_quat(self._quat, other._quat)
if self._single and other._single:
result = result[0]
return self.__class__(result, normalized=True, copy=False)
def inv(self):
"""Invert this rotation.
Composition of a rotation with its inverse results in an identity
transformation.
Returns
-------
inverse : `Rotation` instance
Object containing inverse of the rotations in the current instance.
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Inverting a single rotation:
>>> p = R.from_euler('z', 45, degrees=True)
>>> q = p.inv()
>>> q.as_euler('zyx', degrees=True)
array([-45., 0., 0.])
Inverting multiple rotations:
>>> p = R.from_rotvec([[0, 0, np.pi/3], [-np.pi/4, 0, 0]])
>>> q = p.inv()
>>> q.as_rotvec()
array([[-0. , -0. , -1.04719755],
[ 0.78539816, -0. , -0. ]])
"""
quat = self._quat.copy()
quat[:, -1] *= -1
if self._single:
quat = quat[0]
return self.__class__(quat, normalized=True, copy=False)
def __getitem__(self, indexer):
"""Extract rotation(s) at given index(es) from object.
Create a new `Rotation` instance containing a subset of rotations
stored in this object.
Parameters
----------
indexer : index, slice, or index array
Specifies which rotation(s) to extract. A single indexer must be
specified, i.e. as if indexing a 1 dimensional array or list.
Returns
-------
rotation : `Rotation` instance
Contains
- a single rotation, if `indexer` is a single index
- a stack of rotation(s), if `indexer` is a slice, or and index
array.
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
>>> r = R.from_quat([
... [1, 1, 0, 0],
... [0, 1, 0, 1],
... [1, 1, -1, 0]])
>>> r.as_quat()
array([[ 0.70710678, 0.70710678, 0. , 0. ],
[ 0. , 0.70710678, 0. , 0.70710678],
[ 0.57735027, 0.57735027, -0.57735027, 0. ]])
Indexing using a single index:
>>> p = r[0]
>>> p.as_quat()
array([0.70710678, 0.70710678, 0. , 0. ])
Array slicing:
>>> q = r[1:3]
>>> q.as_quat()
array([[ 0. , 0.70710678, 0. , 0.70710678],
[ 0.57735027, 0.57735027, -0.57735027, 0. ]])
"""
return self.__class__(self._quat[indexer], normalized=True)
@classmethod
def random(cls, num=None, random_state=None):
"""Generate uniformly distributed rotations.
Parameters
----------
num : int or None, optional
Number of random rotations to generate. If None (default), then a
single rotation is generated.
random_state : int, RandomState instance or None, optional
Accepts an integer as a seed for the random generator or a
RandomState object. If None (default), uses global `numpy.random`
random state.
Returns
-------
random_rotation : `Rotation` instance
Contains a single rotation if `num` is None. Otherwise contains a
stack of `num` rotations.
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
Sample a single rotation:
>>> R.random(random_state=1234).as_euler('zxy', degrees=True)
array([-110.5976185 , 55.32758512, 76.3289269 ])
Sample a stack of rotations:
>>> R.random(5, random_state=1234).as_euler('zxy', degrees=True)
array([[-110.5976185 , 55.32758512, 76.3289269 ],
[ -91.59132005, -14.3629884 , -93.91933182],
[ 25.23835501, 45.02035145, -121.67867086],
[ -51.51414184, -15.29022692, -172.46870023],
[ -81.63376847, -27.39521579, 2.60408416]])
"""
random_state = check_random_state(random_state)
if num is None:
sample = random_state.normal(size=4)
else:
sample = random_state.normal(size=(num, 4))
return Rotation.from_quat(sample)
@classmethod
def match_vectors(cls, a, b, weights=None, normalized=False):
"""Estimate a rotation to match two sets of vectors.
Find a rotation between frames A and B which best matches a set of unit
vectors `a` and `b` observed in these frames. The following loss
function is minimized to solve for the direction cosine matrix
:math:`C`:
.. math::
L(C) = \\frac{1}{2} \\sum_{i = 1}^{n} w_i \\lVert \\mathbf{a}_i -
C \\mathbf{b}_i \\rVert^2 ,
where :math:`w_i`'s are the `weights` corresponding to each vector.
The rotation is estimated using Markley's SVD method [1]_.
Parameters
----------
a : array_like, shape (N, 3)
Vector components observed in initial frame A. Each row of `a`
denotes a vector.
b : array_like, shape (N, 3)
Vector components observed in another frame B. Each row of `b`
denotes a vector.
weights : array_like shape (N,), optional
Weights describing the relative importance of the vectors in
`a`. If None (default), then all values in `weights` are assumed to
be equal.
normalized : bool, optional
If True, assume input vectors `a` and `b` to have unit norm. If
False, normalize `a` and `b` before estimating rotation. Default
is False.
Returns
-------
estimated_rotation : `Rotation` instance
Best estimate of the rotation that transforms `b` to `a`.
sensitivity_matrix : ndarray, shape (3, 3)
Scaled covariance of the attitude errors expressed as the small
rotation vector of frame A. Multiply with harmonic mean [3]_ of
variance in each observation to get true covariance matrix. The
error model is detailed in [2]_.
References
----------
.. [1] F. Landis Markley,
"Attitude determination using vector observations: a fast
optimal matrix algorithm", Journal of Astronautical Sciences,
Vol. 41, No.2, 1993, pp. 261-280.
.. [2] F. Landis Markley,
"Attitude determination using vector observations and the
Singular Value Decomposition", Journal of Astronautical
Sciences, Vol. 38, No.3, 1988, pp. 245-258.
.. [3] https://en.wikipedia.org/wiki/Harmonic_mean
"""
a = np.asarray(a)
if a.ndim != 2 or a.shape[-1] != 3:
raise ValueError("Expected input `a` to have shape (N, 3), "
"got {}".format(a.shape))
b = np.asarray(b)
if b.ndim != 2 or b.shape[-1] != 3:
raise ValueError("Expected input `b` to have shape (N, 3), "
"got {}.".format(b.shape))
if a.shape != b.shape:
raise ValueError("Expected inputs `a` and `b` to have same shapes"
", got {} and {} respectively.".format(
a.shape, b.shape))
if b.shape[0] == 1:
raise ValueError("Rotation cannot be estimated using a single "
"vector.")
if weights is None:
weights = np.ones(b.shape[0])
else:
weights = np.asarray(weights)
if weights.ndim != 1:
raise ValueError("Expected `weights` to be 1 dimensional, got "
"shape {}.".format(weights.shape))
if weights.shape[0] != b.shape[0]:
raise ValueError("Expected `weights` to have number of values "
"equal to number of input vectors, got "
"{} values and {} vectors.".format(
weights.shape[0], b.shape[0]))
weights = weights / np.sum(weights)
if not normalized:
a = a / scipy.linalg.norm(a, axis=1)[:, None]
b = b / scipy.linalg.norm(b, axis=1)[:, None]
B = np.einsum('ji,jk->ik', weights[:, None] * a, b)
u, s, vh = np.linalg.svd(B)
C = np.dot(u, vh)
zeta = (s[0]+s[1]) * (s[1]+s[2]) * (s[2]+s[0])
if np.abs(zeta) <= 1e-16:
raise ValueError("Three component error vector has infinite "
"covariance. It is impossible to determine the "
"rotation uniquely.")
kappa = s[0]*s[1] + s[1]*s[2] + s[2]*s[0]
sensitivity = ((kappa * np.eye(3) + np.dot(B, B.T)) /
(zeta * a.shape[0]))
return cls.from_dcm(C), sensitivity
class Slerp(object):
"""Spherical Linear Interpolation of Rotations.
The interpolation between consecutive rotations is performed as a rotation
around a fixed axis with a constant angular velocity [1]_. This ensures
that the interpolated rotations follow the shortest path between initial
and final orientations.
Parameters
----------
times : array_like, shape (N,)
Times of the known rotations. At least 2 times must be specified.
rotations : `Rotation` instance
Rotations to perform the interpolation between. Must contain N
rotations.
Methods
-------
__call__
See Also
--------
Rotation
Notes
-----
.. versionadded:: 1.2.0
References
----------
.. [1] https://en.wikipedia.org/wiki/Slerp#Quaternion_Slerp
Examples
--------
>>> from scipy.spatial.transform import Rotation as R
>>> from scipy.spatial.transform import Slerp
Setup the fixed keyframe rotations and times:
>>> key_rots = R.random(5, random_state=2342345)
>>> key_times = [0, 1, 2, 3, 4]
Create the interpolator object:
>>> slerp = Slerp(key_times, key_rots)
Interpolate the rotations at the given times:
>>> times = [0, 0.5, 0.25, 1, 1.5, 2, 2.75, 3, 3.25, 3.60, 4]
>>> interp_rots = slerp(times)
The keyframe rotations expressed as Euler angles:
>>> key_rots.as_euler('xyz', degrees=True)
array([[ 14.31443779, -27.50095894, -3.7275787 ],
[ -1.79924227, -24.69421529, 164.57701743],
[146.15020772, 43.22849451, -31.34891088],
[ 46.39959442, 11.62126073, -45.99719267],
[-88.94647804, -49.64400082, -65.80546984]])
The interpolated rotations expressed as Euler angles. These agree with the
keyframe rotations at both endpoints of the range of keyframe times.
>>> interp_rots.as_euler('xyz', degrees=True)
array([[ 14.31443779, -27.50095894, -3.7275787 ],
[ 4.74588574, -32.44683966, 81.25139984],
[ 10.71094749, -31.56690154, 38.06896408],
[ -1.79924227, -24.69421529, 164.57701743],
[ 11.72796022, 51.64207311, -171.7374683 ],
[ 146.15020772, 43.22849451, -31.34891088],
[ 68.10921869, 20.67625074, -48.74886034],
[ 46.39959442, 11.62126073, -45.99719267],
[ 12.35552615, 4.21525086, -64.89288124],
[ -30.08117143, -19.90769513, -78.98121326],
[ -88.94647804, -49.64400082, -65.80546984]])
"""
def __init__(self, times, rotations):
if len(rotations) == 1:
raise ValueError("`rotations` must contain at least 2 rotations.")
times = np.asarray(times)
if times.ndim != 1:
raise ValueError("Expected times to be specified in a 1 "
"dimensional array, got {} "
"dimensions.".format(times.ndim))
if times.shape[0] != len(rotations):
raise ValueError("Expected number of rotations to be equal to "
"number of timestamps given, got {} rotations "
"and {} timestamps.".format(
len(rotations), times.shape[0]))
self.times = times
self.timedelta = np.diff(times)
if np.any(self.timedelta <= 0):
raise ValueError("Times must be in strictly increasing order.")
self.rotations = rotations[:-1]
self.rotvecs = (self.rotations.inv() * rotations[1:]).as_rotvec()
def __call__(self, times):
"""Interpolate rotations.
Compute the interpolated rotations at the given `times`.
Parameters
----------
times : array_like, 1D
Times to compute the interpolations at.
Returns
-------
interpolated_rotation : `Rotation` instance
Object containing the rotations computed at given `times`.
"""
# Clearly differentiate from self.times property
compute_times = np.asarray(times)
if compute_times.ndim != 1:
raise ValueError("Expected times to be specified in a 1 "
"dimensional array, got {} "
"dimensions.".format(compute_times.ndim))
# side = 'left' (default) excludes t_min.
ind = np.searchsorted(self.times, compute_times) - 1
# Include t_min. Without this step, index for t_min equals -1
ind[compute_times == self.times[0]] = 0
if np.any(np.logical_or(ind < 0, ind > len(self.rotations) - 1)):
raise ValueError("Interpolation times must be within the range "
"[{}, {}], both inclusive.".format(
self.times[0], self.times[-1]))
alpha = (compute_times - self.times[ind]) / self.timedelta[ind]
return (self.rotations[ind] *
Rotation.from_rotvec(self.rotvecs[ind] * alpha[:, None]))
相关文章:

scipy spatial transform Rotation库的源代码
前几日研究scipy的旋转,不知道具体里面怎么实现的,因此搜索一番。 发现Rotation在scipy的表达是用四元数的 https://github.com/jgagneastro/coffeegrindsize/edit/master/App/dist/coffeegrindsize.app/Contents/Resources/lib/python3.7/scipy/spatia…...
JAVA文件操作
JAVA文件操作 文章目录JAVA文件操作1.属性2.构造方法3.方法3.1创建文件3.2 文件删除3.3创建目录3.4文件名3.5 文件重命名3.6查看文件的可读性 Java中通过 java.io.file类来对文件(目录)进行抽象的描述。注意, 有File对象时,不代表真实存在该文件。1.属…...

字符串匹配 - 模式预处理:BM 算法 (Boyer-Moore)
各种文本编辑器的"查找"功能(CtrlF),大多采用Boyer-Moore算法,效率非常高。算法简介在 1977 年,Robert S. Boyer (Stanford Research Institute) 和 J Strother Moore (Xerox Palo Alto Research Center) 共…...

RV1126笔记三十:freetype显示矢量字体
若该文为原创文章,转载请注明原文出处。 在前面介绍了使用取模软件,可以自定义OSD,这种做法相对不灵活,也无法变更,适用大部分场景。 如果使用opencv需要移植opencv,芯片资源相对要相比好,而且移植比freetype复杂。 这里记录下如何使用freetype显示矢量字体,使用fre…...

polkit pkexec 本地提权漏洞修复方案
polkit pkexec 本地提权漏洞 漏洞细节,polkit pkexec 中对命令行参数处理有误,导致参数注入,能够导致本地提权。 解决建议 1、无法升级软件修复包的,可使用以下命令删除pkexec的SUID-bit权限来规避漏洞风险: chmod 0…...

es-06聚合查询
聚合查询 概念 聚合(aggs)不同于普通查询,是目前学到的第二种大的查询分类,第一种即“query”,因此在代码中的第一层嵌套由“query”变为了“aggs”。用于进行聚合的字段必须是exact value,分词字段不可进行…...

面试知识点准备与总结——(并发篇)
目录线程有哪些状态线程池的核心参数sleep和wait的区别lock 与 synchronized 的异同volatile能否保证线程安全悲观锁和乐观锁的区别Hashtable 与 ConcurrentHashMap 的区别ConcurrentHashMap1.7和1.8的区别ThreadLocal的理解ThreadLocalMap中的key为何要设置为弱引用线程有哪些…...
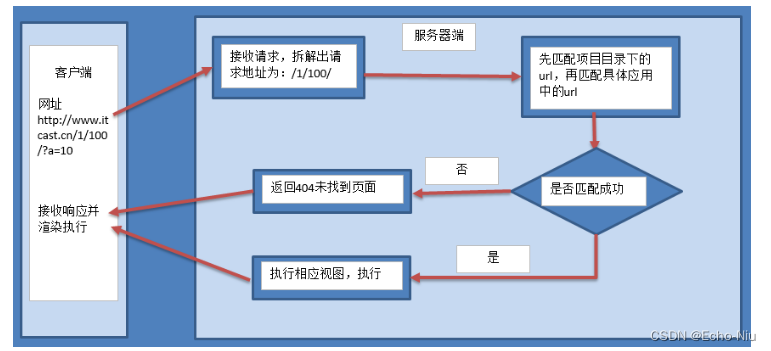
Django框架之模型视图-URLconf
URLconf 浏览者通过在浏览器的地址栏中输入网址请求网站对于Django开发的网站,由哪一个视图进行处理请求,是由url匹配找到的 配置URLconf 1.settings.py中 指定url配置 ROOT_URLCONF 项目.urls2.项目中urls.py 匹配成功后,包含到应用的urls…...
操作系统闲谈06——进程管理
操作系统闲谈06——进程管理 一、进程调度 01 时间片轮转 给每一个进程分配一个时间片,然后时间片用完了,把cpu分配给另一个进程 时间片通常设置为 20ms ~ 50ms 02 先来先服务 就是维护了一个就绪队列,每次选择最先进入队列的进程&#…...

DaVinci 偏好设置:用户 - UI 设置
偏好设置 - 用户/ UI 设置Preferences - User/ UI Settings工作区选项Workspace Options语言Language指定 DaVinci Resolve 软件界面所使用的语言。目前支持英语、简体中文、日语、西班牙语、葡萄牙语、法语、俄语、泰语和越南语等等。启动时重新加载上一个工作项目Reload last…...
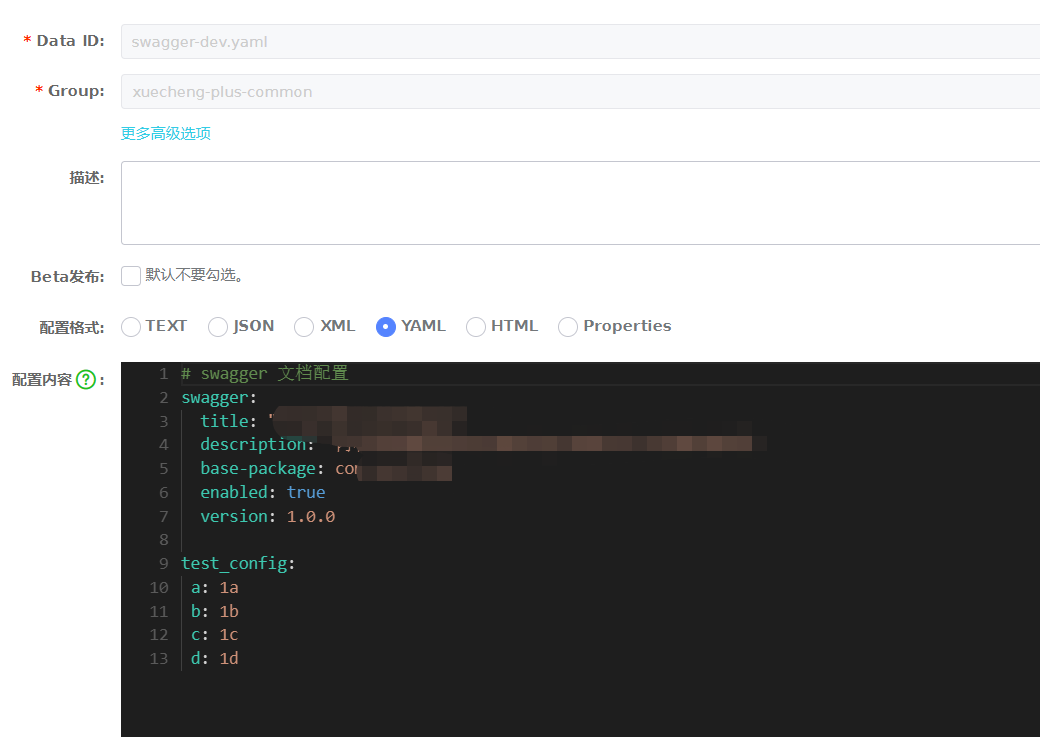
Nacos超简单-管理配置文件
优点理论什么的就不说了,按照流程开始配配置吧。登录Centos,启动Naocs,使用sh /data/soft/restart.sh将自动启动Nacos。访问:http://192.168.101.65:8848/nacos/账号密码:nacos/nacos分为两部分,第一部分准…...
基于微信小程序的中国各地美食推荐平台小程序
文末联系获取源码 开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.…...

如何优雅的导出函数
在开发过程中,经常会引用外部函数。方法主要有两种: 方法一:包含头文件并制定lib位置 优点:使用简单缺点:lib和vs版本有关,不同的版本和编译模式可能导致编译失败 方法二:GetProcAddress 优…...

c++多重继承
1.概论多重继承是否有必要吗?这个问题显然是一个哲学问题,正确的解答方式是根据情况来看,有时候需要,有时候不需要,这显然是一句废话,有点像上马克思主义哲学或者中庸思。但是这个问题和那些思想一样&#…...
15_FreeRtos计数信号量优先级翻转互斥信号量
目录 计数型信号量 计数型信号量相关API函数 计数型信号量实验源码 优先级翻转简介 优先级翻转实验源码 互斥信号量 互斥信号量相关API函数 互斥信号量实验源码 计数型信号量 计数型信号量相当于队列长度大于1的队列,因此计数型信号量能够容纳多个资源,这在…...
二叉树(一)
二叉树(一)1.树的概念2.树的相关概念3.树的表示4.树在实际中的运用5.二叉树概念及结构6.特殊的二叉树7.二叉树的性质🌟🌟hello,各位读者大大们你们好呀🌟🌟 🚀🚀系列专栏…...
【SCL】1200案例:天塔之光数码管显示液体混合水塔水位
使用scl编写天塔之光&数码管显示&液体混合&水塔水位 文章目录 目录 文章目录 前言 一、案例1:天塔之光 1.控制要求 2.编写程序 3.效果 二、案例2:液体混合 1.控制要求 2.编写程序 三、案例3:数码管显示 1.控制要求 2.编写程序 3…...
5.1配置IBGP和EBGP
5.2.1实验1:配置IBGP和EBGP 实验目的 熟悉IBGP和EBGP的应用场景掌握IBGP和EBGP的配置方法 实验拓扑 实验拓扑如图5-1所示: 图5-1:配置IBGP和EBGP 实验步骤 IP地址的配置 R1的配置 <Huawei>system-view Enter system view, return …...
c++中超级详细的一些知识,新手快来
目录 2.文章内容简介 3.理解虚函数表 3.1.多态与虚表 3.2.使用指针访问虚表 4.对象模型概述 4.1.简单对象模型 4.2.表格驱动模型 4.3.非继承下的C对象模型 5.继承下的C对象模型 5.1.单继承 5.2.多继承 5.2.1一般的多重继承(非菱形继承) 5.2…...

[答疑]经营困难时期谈建模和伪创新-长点心和长点良心
leonll 2022-11-26 9:53 我们今年真是太难了……(此处删除若干字)……去年底就想着邀请您来给我们讲课,现在也没有实行。我想再和我们老大提,您觉得怎么说个关键理由,这样的形势合适引进UML开发流程? UML…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
