【CSAPP】整数表示
文章目录
- 整型数据类型
- 无符号数的编码
- 补码编码
- 确定大小的整数类型
- 练习1
- 练习2
- 有符号数和无符号数之间的转换
- 练习
- C语言中的有符号数与无符号数
- 练习
- 扩展一个数字的位表示
- 练习1
- 练习2
- 截断数字
- 练习
- 关于有符号数与无符号数的建议
- 练习1
- 练习2
使用 位编码整数有两种不同的方式:
- 只能表示非负数(零、正数),即无符号数的编码。
- 既能表示非负数,也能表示负数,即有符号数的编码、补码编码。
下表是一些数学术语,用于精确定义和描述计算机如何编码和操作整数。
| 符号 | 类型 | 含义 |
|---|---|---|
| B2TwB2T_wB2Tw | 函数 | 二进制转补码 |
| B2UwB2U_wB2Uw | 函数 | 二进制转无符号数 |
| U2BwU2B_wU2Bw | 函数 | 无符号数转二进制 |
| U2TwU2T_wU2Tw | 函数 | 无符号数转补码 |
| T2BwT2B_wT2Bw | 函数 | 补码转二进制 |
| T2UwT2U_wT2Uw | 函数 | 补码转无符号数 |
| TMinwTMin_wTMinw | 常数 | 最小补码值 |
| TMaxwTMax_wTMaxw | 常数 | 最大补码值 |
| UMaxwUMax_wUMaxw | 常数 | 最大无符号数 |
| +wt+^{t}_{w}+wt | 操作 | 补码加法 |
| +wu+^{u}_{w}+wu | 操作 | 无符号数加法 |
| ∗wt*^{t}_{w}∗wt | 操作 | 补码乘法 |
| ∗wu*^{u}_{w}∗wu | 操作 | 无符号数乘法 |
| −wt-^{t}_{w}−wt | 操作 | 补码取反 |
| −wu-^{u}_{w}−wu | 操作 | 无符号数取反 |
下标
w表示整数的位数。
整型数据类型
C语言支持多种整型数据类型——表示有限范围的整数。每种类型都可以用关键字指定大小,如char、short、long,同时还可以用unsigned表示是无符号的。
无符号数永远是>=0的。有符号数既能表示负数,又能表示非负数,在“典型”实现中,负数的表示范围比非负数大1(不对称)。
C语言标准定义了每种数据类型必须能够表示的最小取值范围。对有些数据类型则要求正数和负数的取值范围是对称的。
C/C++支持无符号数和有符号数,Java只支持有符号数。
无符号数的编码
假设一个整数有w位,其编码为[xw−1,xw−2,...,x0][x_{w-1}, x_{w-2}, ... , x_0][xw−1,xw−2,...,x0],写作位向量x⃗\vec xx。在这个编码中,每个位xix_ixi取值为0或1。
原理:无符号数的编码定义。
对向量x⃗=[xw−1,xw−2,...,x0]\vec x = [x_{w-1}, x_{w-2}, ... , x_0]x=[xw−1,xw−2,...,x0],有
B2Uw(x⃗)=˙∑i=0w−1xi2i\begin{align} B2U_w(\vec x) \.=\displaystyle\sum_{i=0}^{w-1}x_i2^i \end{align} B2Uw(x)=˙i=0∑w−1xi2i
=˙\.==˙表示左边被定义为等于右边。
函数 B2Uw(x⃗)B2U_w(\vec x)B2Uw(x)将一个长度为w的0、1串映射为非负整数,函数的返回值就是该编码的无符号数值。
x⃗\vec xx所能表示的最小值为[0, 0, ..., 0],w个0,该编码对应的无符号数值为0;最大值是[1, 1, ..., 1],w个1,该编码对应的无符号数值为 UMaxw=˙B2Uw([1,1,...,1])=∑i=0i=w−12i=2w−1UMax_w \.= B2U_w([1, 1, ..., 1]) = \displaystyle\sum_{i=0}^{i=w-1}2^{i} = 2^w - 1UMaxw=˙B2Uw([1,1,...,1])=i=0∑i=w−12i=2w−1。
因此,函数B2UwB2U_wB2Uw能够被定义为一个映射:{0,1}w→{0,1,2,...,2w−1}\{0, 1\}^w \to \{0, 1, 2, ..., 2^{w}-1\}{0,1}w→{0,1,2,...,2w−1}。
原理:无符号数编码是唯一的。
函数B2UwB2U_wB2Uw是一个双射。
对函数 B2Uw(x⃗)B2U_w(\vec x)B2Uw(x)而言,给定一个位向量x⃗\vec xx,有唯一对应的无符号数值。
对函数 U2Bw(y)U2B_w(y)U2Bw(y)而言,给定一个无符号数值yyy,有唯一对应的位向量x⃗\vec xx。
补码编码
最常见的有符号数的计算机表示方法是补码编码。在这个定义中,将最高有效位解释为负权。
原理:补码编码定义。
对向量x⃗=[xw−1,xw−2,...,x0]\vec x = [x_{w-1}, x_{w-2}, ... , x_0]x=[xw−1,xw−2,...,x0],有
B2Tw(x⃗)=˙−xw−12w−1+∑i=0w−2xi2i\begin{align} B2T_w(\vec x) \.=-x_{w-1}2^{w-1} + \displaystyle\sum_{i=0}^{w-2}x_i2^i \end{align} B2Tw(x)=˙−xw−12w−1+i=0∑w−2xi2i
最高有效位xw−1x_{w-1}xw−1也称为符号位,它的权重为−2w−1-2^{w-1}−2w−1。xw−1x_{w-1}xw−1为1时,该值是负数;为0时,该值是非负数。
x⃗\vec xx所能表示的最小值为[1, 0, ..., 0],值为TMinw=˙−2w−1TMin_w\.=-2^{w-1}TMinw=˙−2w−1;最大值为[0, 1, ..., 1],值为TMaxw=2w−1−1TMax_w=2^{w-1}-1TMaxw=2w−1−1。
因此,函数B2TwB2T_wB2Tw能够被定义为一个映射:{0,1}w→{−2w−1,−2w−1+1,...,2w−1−2,2w−1−1}\{0, 1\}^w \to \{-2^{w-1}, -2^{w-1} + 1, ..., 2^{w-1}-2, 2^{w-1}-1\}{0,1}w→{−2w−1,−2w−1+1,...,2w−1−2,2w−1−1}。
原理:补码编码是唯一的。
函数B2TwB2T_wB2Tw是一个双射。
对函数 B2Tw(x⃗)B2T_w(\vec x)B2Tw(x)而言,给定一个位向量x⃗\vec xx,有唯一对应的有符号数值。
对函数 T2Bw(y)T2B_w(y)T2Bw(y)而言,给定一个有符号数值yyy,有唯一对应的位向量x⃗\vec xx。
相同的位向量 x⃗\vec xx 在不同的语境下有不同的含义。
如果 x⃗\vec xx 是[1, 1, ..., 1]的串,无符号数值语境下表示UMax,有符号数值语境下表示-1。
如果 x⃗\vec xx 是[1, 0, ..., 0]的串,无符号数值下表示正数 2w−12^{w-1}2w−1,有符号数值下表示负数 −2w−1-2^{w-1}−2w−1
最高位为0的情况下,无符号数值和有符号数值相等。
C语言标准并没有要求采用补码形式表示有符号数,但几乎所有的机器都是这么做的。如果程序员希望代码具有最大的可移植性,那么就该假定有符号数是采用补码编码的。
补码:对于非负数
x,用2w−x2^w - x2w−x的值表示-x。
反码:对于非负数x,用2w−1−x2^w - 1 - x2w−1−x的值表示-x。
确定大小的整数类型
ISO C99标准定义了确定大小的整数类型。如int32_t和uint64_t。无论在哪台机器上,它们都分别表示32位的有符号数和64位的无符号数。标准也定义了诸如INT32_MAX、INT32_MIN、UINT64_MAX这样的宏,表示对应整数类型值的范围。标准也定义了诸如PRId32、PRIu64这样的宏,表示格式化打印相应的整型变量时的宽度。
相比于
C/C++,Java标准定义更明确一些:仅支持有符号数、整型的表示范围确定、采用补码编码。
练习1
位向量 x⃗\vec xx 的长度w = 4,填写下表。
| 位向量 x | B2U | B2T | |
| 十六进制 | 二进制 | ||
| 0xE | [1110] | 14 | -2 |
| 0x0 | [0000] | 0 | 0 |
| 0x5 | [0101] | 5 | 5 |
| 0x8 | [1000] | 8 | -8 |
| 0xD | [1101] | 13 | -3 |
| 0xF | [1111] | 15 | -1 |
练习2
将下列使用32位补码表示的16进制数转换成等价的10进制数。
- 0x2e0
736 - -0x58
-88 - 0x28
40 - -0x30
-48 - 0x78
120 - 0x88
136 - 0x1f8
504 - 0xc0
192 - -0x48
-72
有符号数和无符号数之间的转换
相同位宽的有符号数和无符号数之间强制类型转换的结果是底层位值不变,但改变了解释这些位的方式。比如把short类型的-12345转换成unsigned short会得到53191,事实上这两个数的底层位值是一模一样的。再比如把UINT_MAX强转为有符号数会得到-1,UINT_MAX和-1的底层位值都是[1, 1, ..., 1]。
因此,我们可以通过分析二进制表示,完成有符号数和无符号数之间的转换。
原理:从有符号数转无符号数。
对于位宽为w的有符号数xxx,二进制表示为位向量 x⃗\vec xx,满足TMinw<=x<=TMaxwTMin_w <=x<= TMax_wTMinw<=x<=TMaxw,有:
T2Uw(x)=˙B2Uw(T2Bw(x))=x+xw−12w={x+2w,x<0x,x>=0\begin{align} T2U_w(x)\.=B2U_w(T2B_w(x))= x+x_{w-1}2^w= \begin{cases} x+2^w, \quad &x<0 \\ x, \quad &x>=0 \end{cases} \end{align} T2Uw(x)=˙B2Uw(T2Bw(x))=x+xw−12w={x+2w,x,x<0x>=0
有符号数的最高位权值是−2w−1-2^{w-1}−2w−1,无符号数的最高位权值是2w−12^{w-1}2w−1,两者相差2w2^{w}2w。所以当最高位为
1(x<0x<0x<0)时,无符号数值比有符号数值大2w2^{w}2w。
原理:从无符号数转有符号数。
对于位宽为w的无符号数xxx,二进制表示为位向量 x⃗\vec xx,满足0<=x<=UMaxw0<=x<= UMax_w0<=x<=UMaxw,有:
U2Tw(x)=˙B2Tw(U2Bw(x))=x−xw−12w={x,x<=TMaxwx−2w,x>TMaxw\begin{align} U2T_w(x)\.=B2T_w(U2B_w(x))=x-x_{w-1}2^w= \begin{cases} x, \quad &x<=TMax_w \\ x-2^w, \quad &x>TMax_w \end{cases} \end{align} U2Tw(x)=˙B2Tw(U2Bw(x))=x−xw−12w={x,x−2w,x<=TMaxwx>TMaxw
当最高位为
1(x>TMaxwx>TMax_wx>TMaxw)时,有符号数比无符号数小2w2^w2w。
练习
补充下面的表格。
| xxx | T2U4(x)T2U_4(x)T2U4(x) |
|---|---|
| -8 | 8 |
| -3 | 13 |
| -2 | 14 |
| -1 | 15 |
| 0 | 0 |
| 5 | 5 |
C语言中的有符号数与无符号数
在C语言中,声明一个常量时,默认是有符号的,如123、0xAB。要创建无符号常量,需要加上后缀字符u或U,如123u、0xABu。
可以显示转换,如:
int i;
unsigned int u;i = (int)u;
u = (unsigned int)i;
可以隐式转换,如:
int i;
unsigned int u;i = u;
u = i;
或
int i;
unsigned int u;printf("%u\n", i);
printf("%d\n", u);
当执行一个运算时,如果它的一个运算数是有符号的,另一个运算数是无符号的,那么C语言会隐式地将有符号参数转换为无符号数,再进行无符号数之间的运算。
练习
假设在采取补码运算的32位机器上执行以下运算,填写运算的类型和结果。
| 表达式 | 类型 | 求值 |
|---|---|---|
| -2147483647-1 == 2147483648U | 无符号 | 1 |
| -2147483647-1 < 2147483647 | 有符号 | 1 |
| -2147483647-1U < 2147483647 | 无符号 | 0 |
| -2147483647-1 < -2147483647 | 有符号 | 1 |
| -2147483647-1U < -2147483647 | 无符号 | 1 |
扩展一个数字的位表示
要将一个无符号整数转换为一个更大的数据类型,只需要简单地在高位加0,这种运算被称为无符号数的零扩展。
要将一个有符号整数转换为一个更大地数据类型,需要在高位加符号位,这种运算被称为补码的符号扩展。
当数据扩展和有无符号转换同时出现时,C标准要求先扩展、后进行有无符号转换。
short sx = -12345;
unsigned int uy = sx; // 等价于unsigned int uy = (unsigned int)(int)sx;
// uy的十六进制表示为0xFFFFCFC7
如果先做符号转换、再扩展,那
uy的十六进制表示为0x0000CFC7,就无法正确表示原值sx的符号位。
练习1
下面各个补码对应的有符号数值是多少?
- [1011]
−23+21+20=−5-2^3+2^1+2^0=-5−23+21+20=−5 - [11011]
−24+23+21+20=−5-2^4+2^3+2^1+2^0=-5−24+23+21+20=−5 - [111011]
−25+24+23+21+20=−5-2^5+2^4+2^3+2^1+2^0=-5−25+24+23+21+20=−5
后两个有符号数分别是第一个有符号数符号扩展
1位和2位的结果。符号扩展不会改变补码表示的数值大小。
练习2
考虑下面的C函数:
int fun1(unsigned word)
{return (int)((word << 24) >> 24);
}int fun2(unsigned word)
{return ((int)word << 24) >> 24;
}
填写下表。
| www | fun1(w)fun1(w)fun1(w) | fun2(w)fun2(w)fun2(w) |
|---|---|---|
| 0x00000076 | 0x00000076 | 0x00000076 |
| 0x87654321 | 0x00000021 | 0x00000021 |
| 0x000000C9 | 0x000000C9 | 0xFFFFFFC9 |
| 0xEDCBA987 | 0x00000087 | 0xFFFFFF87 |
截断数字
当将一个w位的数截断为一个k位的数时,会丢弃高w-k位,并对低k位做新的解释。截断一个数可能会改变它的值(即溢出)。
练习
将一个4位数值截断为一个3位数值,填写下表。
| 十六进制 | 无符号(十进制) | 补码(十进制) | |||
| 原始值 | 截断值 | 原始值 | 截断值 | 原始值 | 截断值 |
| 0x0 | 0x0 | 0 | 0 | 0 | 0 |
| 0x2 | 0x2 | 2 | 2 | 2 | 2 |
| 0x9 | 0x1 | 9 | 1 | -7 | 1 |
| 0xB | 0x3 | 11 | 3 | -5 | 3 |
| 0xF | 0x7 | 15 | 7 | -1 | -1 |
关于有符号数与无符号数的建议
整数的扩展和截断、有符号数和无符号数之间的隐式转换,会导致程序错误或漏洞。而这些不符合预期的行为有时很难被程序员发现。避免这些错误的方法有:
- 整数运算时,统一符号。
- 如果涉及到整数类型的变化,使用强制转换代替隐式转换,方便程序员发现问题。
练习1
考虑下面的代码,当length等于0时,预期结果是0.0。但实际上,运行时会造成一个内存错误。为什么?该如何修改代码?
float sum_elements(float a[], unsigned length)
{float result = 0;for (int i = 0; i <= length - 1; ++i) {result += a[i];}return result;
}
length是无符号数,i是有符号数,程序执行i <= length - 1时,程序会按无符号数执行该运算。
当length = 0时,在无符号数的语境下,length - 1等于UINT_MAX,i的值永远小于UINT_MAX,所以程序会访问未知内存,导致运行时错误。
解决办法是:
- 把
length的类型改为int。当length = 0时,在有符号数的语境下,length - 1等于-1,i的值是0,程序立即返回0.0。 - 把
i <= length - 1改为i < length。
练习2
下面的代码用来判断一个字符串是否比另一个更长。在头文件stdio.h中,size_t是无符号整型。
// 库函数
size_t strlen(const char *s);// 用户代码
int strlonger(char *s, char *t)
{return strlen(s) - strlen(t) > 0;
}
- 在什么情况下,这个函数会产生不正确的结果?为什么?
如果strlen(s)小于strlen(t),strlen(s) - strlen(t)的预期结果应该是个负数,strlen(s) - strlen(t) > 0的预期结果应该是0。
但strlen(s)和strlen(t)的返回值都是无符号数,strlen(s) - strlen(t)的结果也是无符号数,无符号数一定是>=0的。因此程序会返回1,而不是0,和预期不符。 - 如何修改代码,使其正确。
把return strlen(s) - strlen(t) > 0;改为return strlen(s) > strlen(t);
相关文章:

【CSAPP】整数表示
文章目录整型数据类型无符号数的编码补码编码确定大小的整数类型练习1练习2有符号数和无符号数之间的转换练习C语言中的有符号数与无符号数练习扩展一个数字的位表示练习1练习2截断数字练习关于有符号数与无符号数的建议练习1练习2使用 位编码整数有两种不同的方式:…...
Python基础2
1. python函数定义 函数定义语法: def 函数名(传入参数): 函数体 return 返回值 —————————————— 参数如果不需要,可以省略返回值如果不需要,可以省略函数必须先定义在使用 注意ÿ…...

【项目立项管理】
项目立项管理 很杂,可以根据左边的列表查看自己不会的 。。。 立项管理主要是解决项目的组织战略符合性问题 开发所需的成本和资源属于经济可行性 承建方组织资源和项目的匹配程度 内部立项目的: 为项目进行资源分配,确定项目绩效目标&am…...

【验证码的识别】—— 极验验证码的识别
前言 (结尾有彩蛋欧) 目前,许多网站采取各种各样的措施来反爬虫,其中一个措施便是使用验证码。随着技术的发展,验证码的花样越来越多。验证码最初是几个数字组合的简单的图形验证码,后来加入了英文字母和混…...
 | 机试题算法思路 【2023】)
华为OD机试 -旋转骰子(Python) | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 卡片组成的最大数字(Python) | 机试题算法思路 华为OD机试 - 网上商城优惠活动(一)(Python) | 机试题算法思路 华为OD机试 - 统计匹配的二元组个数(Python) | 机试题算法思路 华为OD机试 - 找到它(Python) | 机试题算法思路 华为OD机试…...

C生万物 | 模拟实现库函数strcpy之梅开n度
文章目录【梅开一度】:观察库函数strcpy()的实现【梅开二度】:模仿实现strcpy()【梅开三度】:优化简练代码【梅开四度】:assert()断言拦截【梅开五度】:const修饰常量指针【梅开六度】:还可以有返回值哦&am…...
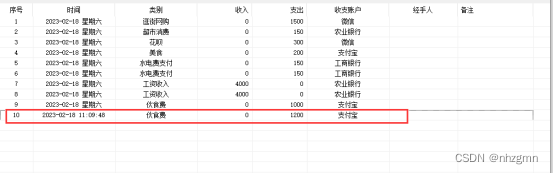
家庭理财,轻松记账修改收支记录这样操作
我们在记账的时候难免会出现记错或者想修改的地方,又或者是想将之前太久没有用的记账记录删除掉,今天,小编就教大家如何修改收支记录,一起接着往下看吧! 第一步,运行【晨曦记账本】在软件主界面中ÿ…...
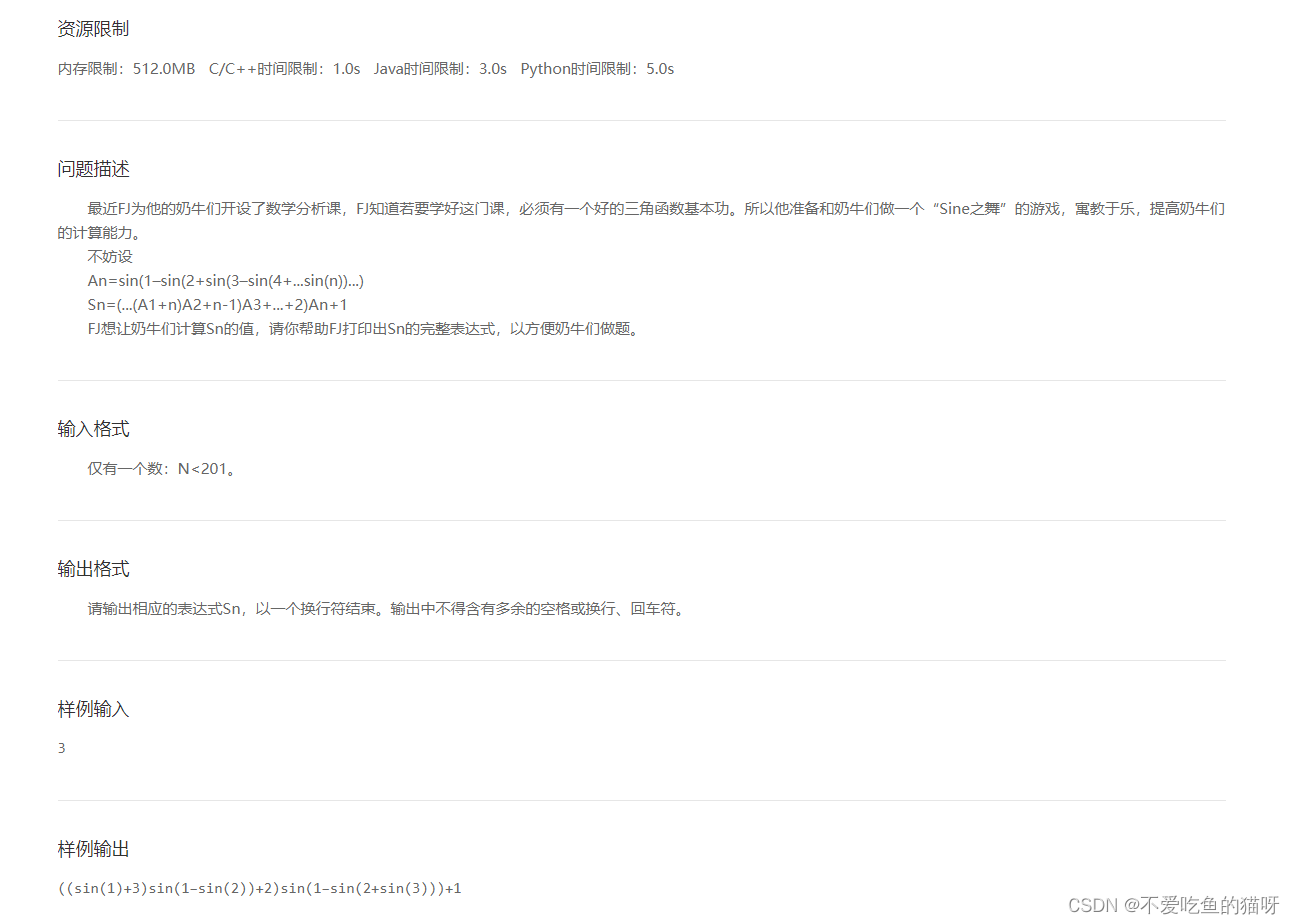
河南工程学院2.17蓝桥杯培训
乘法口诀数列:https://www.acwing.com/problem/content/3466/ 剪绳子:https://www.acwing.com/problem/content/68Sin SinSine之舞:http://lx.lanqiao.cn/problem.page?gpidD5272 数列:https://www.acwing.com/problem/content/…...

【JavaSE】数据类型与变量
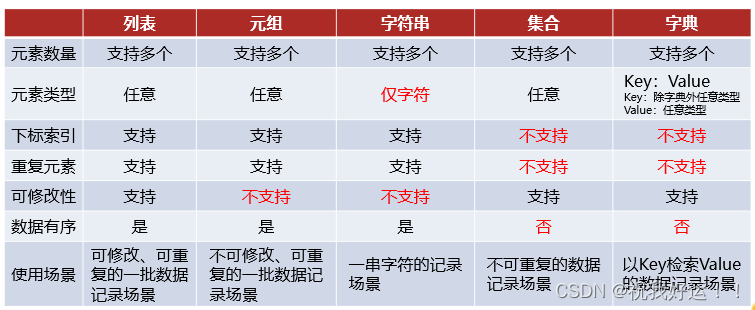
JAVA之父:詹姆斯高斯林 (James Gosling) 前言: 大家好,我是程序猿爱打拳。今天我给大家讲解的是Java基础中的数据类型。主要讲解的是各个类型的应用场景以及注意事项。 目录 1.数据类型 2.常量与变量 2.1常量 2.2变…...

生成模型技术发展过程
生成模型生成模型和判别模型的差异生成模型的目标是在给定了数据集D,并且假设这个数据集的底层分布(underlying distribution)是Pdata,我们希望够近似出这个数据分布。如果我们能够学习到一个好的生成模型,我们就能用这个生成模型为下游任务做…...
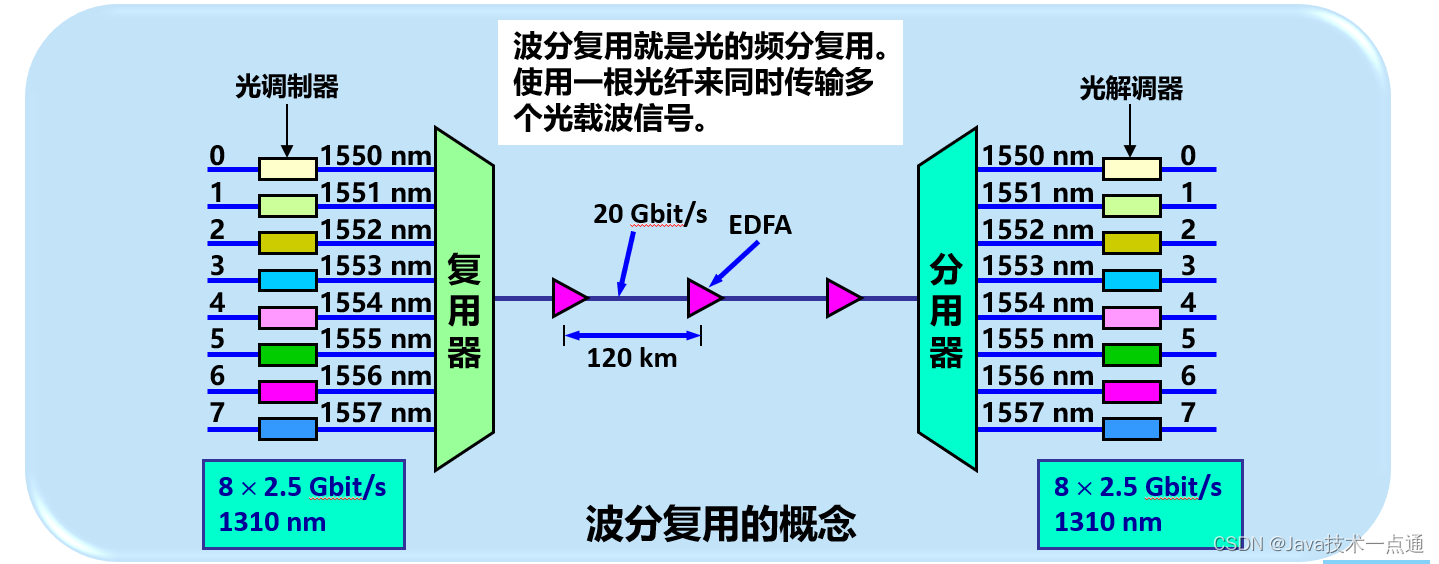
计算机网络第2章(物理层)学习笔记
❤ 作者主页:欢迎来到我的技术博客😎 ❀ 个人介绍:大家好,本人热衷于Java后端开发,欢迎来交流学习哦!( ̄▽ ̄)~* 🍊 如果文章对您有帮助,记得关注、点赞、收藏、…...

4564: 保留尾部*
描述规定输入的字符串中只包含字母和*号,除了尾部的*号之外,请将字符串中其他*号全部删除。输入输入数据包括一串字符串,只包含字母和*,总长度不超过80。输出输出按要求删除*后的字符串。样例输入*******A*BC*DEF*G****样例输出AB…...
安卓项目搭建grpc环境
本篇文章使用的IDE是Android Studio。这里先吐槽一句,安卓项目搭建grpc环境,不管是引入插件还是引入第三方库,对于版本的要求都极为苛刻,一旦版本不匹配就会报错,所以对于版本的搭配一定要注意。 下面介绍的这个版本搭…...
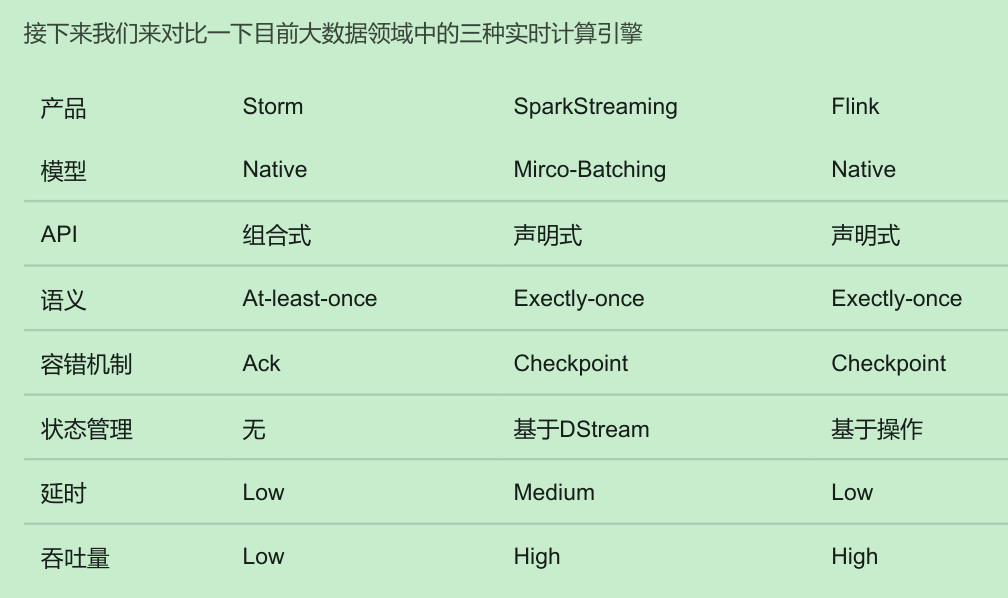
Flink01: 基本介绍
一、什么是Flink 1. Flink是一个开源的分布式,高性能,高可用,准确的流处理框架 (1)分布式:表示flink程序可以运行在很多台机器上, (2)高性能:表示Flink处理性…...

设计模式之单例模式
文章の目录一、什么是单例模式二、如何实现单例模式1、利用JavaScript中的全局对象2、静态成员改造参考写在最后一、什么是单例模式 单例模式也称为单体模式,保证一个类仅有一个实例,并提供一个访问它的全局访问点。 举个栗子:一个班级只有一…...

[oeasy]python0086_ASCII_出现背景_1963年_DEC_PDP系列主机_VT系列终端
编码进化 回忆上次内容 上次 回顾了 字符编码的新陈代谢 ibm 曾经的EBCDIC 由于 字符不连续导致 后续 出现无数问题 随着 网络的发展 数据交换的 需要原来的小隐患现在 产生了 巨大问题 Bemer 联合各方巨头 想要推出 字符连续的编码集 这新编码集 具体长什么样 呢࿱…...
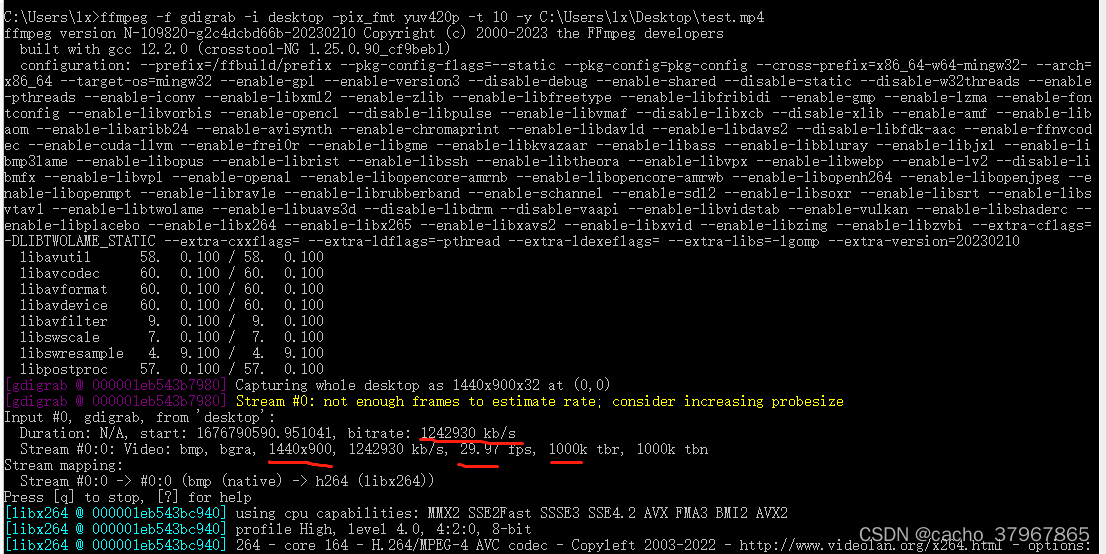
基于FFmpeg实现的无声音屏幕录制
UI自动化测试时,有时需要进行录屏操作,这时我们是不需要声音的,我们可以通过FFmpeg进行简单的录制工作。 以下是在windows10环境下,基于FFmpeg实现的简单录制: Ffmpeg简介: 功能:有非常强大的…...
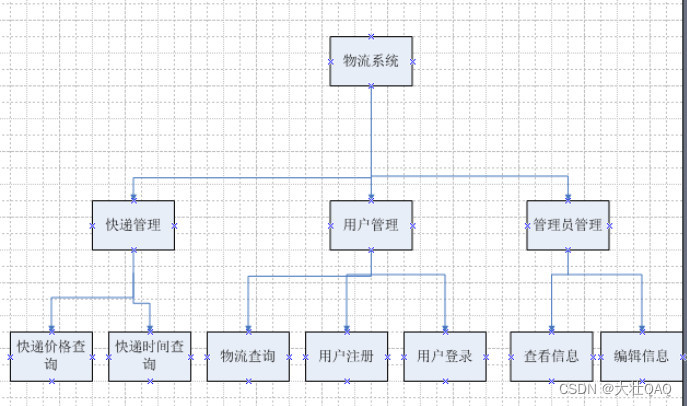
【项目精选】基于JSP物流信息网(论文+源码+视频)
点击下载源码 近年来,随着时代的进步,社会随之不断发展,经济也快速发展起来了,人民的消费水平在不断地提高,平常的实体店消费已经不能满足人们的需求;在者,互联网技术的不断发展也为电子商务的兴…...
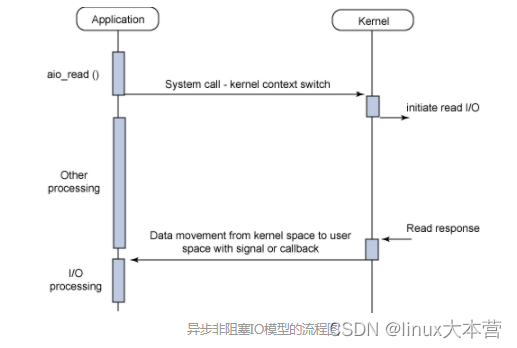
linux异步IO编程实例分析
在Direct IO模式下,异步是非常有必要的(因为绕过了pagecache,直接和磁盘交互)。linux Native AIO正是基于这种场景设计的,具体的介绍见:KernelAsynchronousI/O (AIO)SupportforLinux。下面我们就来分析一下…...
)
日常英语口语练习-情景交际场景25(三)
登山踏青m: hey Carol, what are you doing this weekend?o: im going hiking /haikiŋ/登山with my husband and our hiking clubm: you have a hiking culb?o: yes, we do, we have 30 to 40 people of all ages and skill levelsm: thats great, do you gus do…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
