[保研/考研机试] KY26 10进制 VS 2进制 清华大学复试上机题 C++实现
题目链接:
10进制 VS 2进制![]() http://www.nowcoder.com/share/jump/437195121691738172415
http://www.nowcoder.com/share/jump/437195121691738172415
描述
对于一个十进制数A,将A转换为二进制数,然后按位逆序排列,再转换为十进制数B,我们称B为A的二进制逆序数。 例如对于十进制数173,它的二进制形式为10101101,逆序排列得到10110101,其十进制数为181,181即为173的二进制逆序数。
输入描述:
一个1000位(即10^999)以内的十进制数。
输出描述:
输入的十进制数的二进制逆序数。
示例1
输入:
173输出:
181思路:
- 输入一个十进制数
s。 - 使用大整数除法函数
divide将s不断除以 2,得到二进制数的各个位,存放在向量binary中,顺序是按位逆序排列的。 - 初始化一个字符串
res为 "0",用于存放最终的结果。 - 遍历
binary中的每一位,将res乘以 2(相当于左移一位),然后加上当前位的值,得到二进制逆序数的十进制表示。 - 输出最终的二进制逆序数。
注意:代码中使用了字符串来表示大整数,通过模拟除法、乘法和加法操作,实现了对二进制逆序数的计算和转换。
源代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;// 例题6.3 KY26 10进制 VS 2进制 // 字符串表示的大整数除法
string divide(string str, int x) {int reminder = 0; // 余数for (int i = 0; i < str.size(); i++) {int current = reminder * 10 + str[i] - '0'; // 当前位的数值str[i] = current / x + '0'; // 更新当前位的值为商的字符表示reminder = current % x; // 更新余数}int pos = 0;while (str[pos] == '0') {pos++; // 移除前导零}return str.substr(pos); // 返回除法结果,移除前导零
}string multiple(string str, int x) {int carry = 0; // 进位for (int i = str.size() - 1; i >= 0; i--) {int current = x * (str[i] - '0') + carry; // 当前位的计算结果str[i] = current % 10 + '0'; // 更新当前位的值为计算结果的个位carry = current / 10; // 更新进位}if (carry != 0) {str = "1" + str; // 处理最终的进位}return str;
}string Add(string str, int x) {int carry = x; // 初始进位为 xfor (int i = str.size() - 1; i >= 0; i--) {int current = (str[i] - '0') + carry; // 当前位的计算结果str[i] = current % 10 + '0'; // 更新当前位的值为计算结果的个位carry = current / 10; // 更新进位}if (carry != 0) {str = "1" + str; // 处理最终的进位}return str;
}int main() {string s;cin >> s; // 输入十进制数vector<int> binary; // 用于存放二进制逆序的每一位while (s.size() != 0) {int last = s[s.size() - 1] - '0'; // 取最后一位binary.push_back(last % 2); // 将最后一位的余数(二进制的最低位)存入 vectors = divide(s, 2); // 将十进制数除以 2,得到下一轮迭代的数值}// 将得到的 binary 中的按位逆序排列的二进制数转换为十进制数string res = "0"; // 初始化结果为 0for (int i = 0; i < binary.size(); i++) {res = multiple(res, 2); // 将结果乘以 2,相当于左移一位res = Add(res, binary[i]); // 加上当前位的值}cout << res << endl; // 输出最终的二进制逆序数return 0;
}
提交结果:
相关文章:

[保研/考研机试] KY26 10进制 VS 2进制 清华大学复试上机题 C++实现
题目链接: 10进制 VS 2进制http://www.nowcoder.com/share/jump/437195121691738172415 描述 对于一个十进制数A,将A转换为二进制数,然后按位逆序排列,再转换为十进制数B,我们称B为A的二进制逆序数。 例如对于十进制…...
JSP-学习笔记
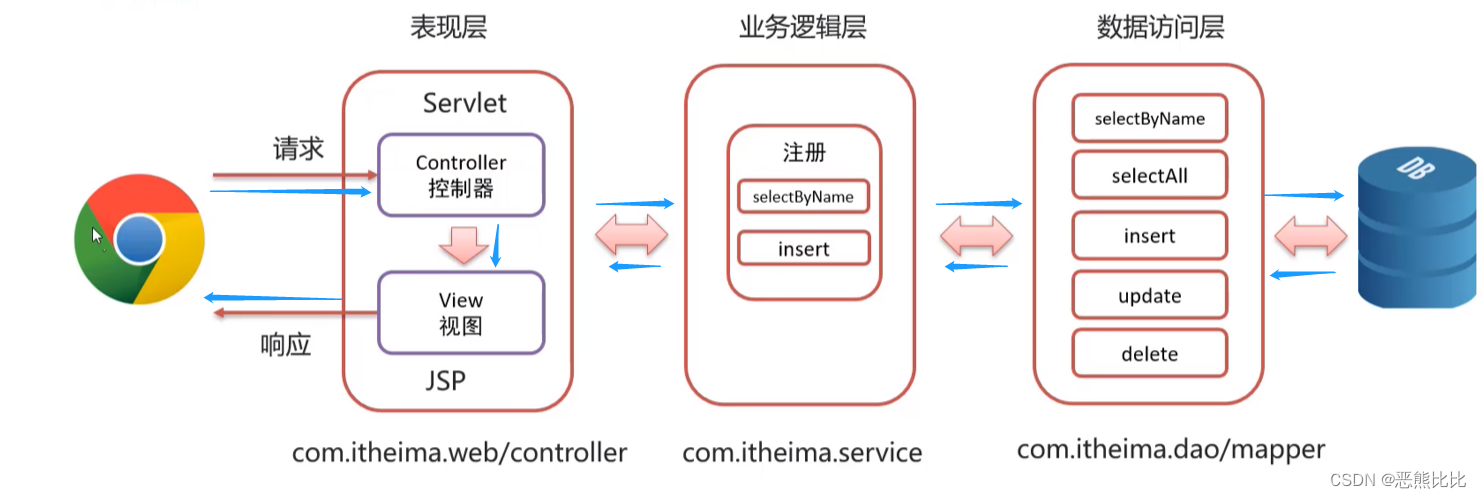
文章目录 1.JSP介绍2 JSP快速入门3 JSP 脚本3.1 JSP脚本案例3.2 JSP缺点 4 EL表达式4.1 快速入门案例 5. JSTL标签6. MVC模式和三层架构6.1 MVC6.2 三层架构 7. 案例-基于MVC和三层架构实现商品表的增删改查 1.JSP介绍 概念 JSP(JavaServer Pages)是一种…...
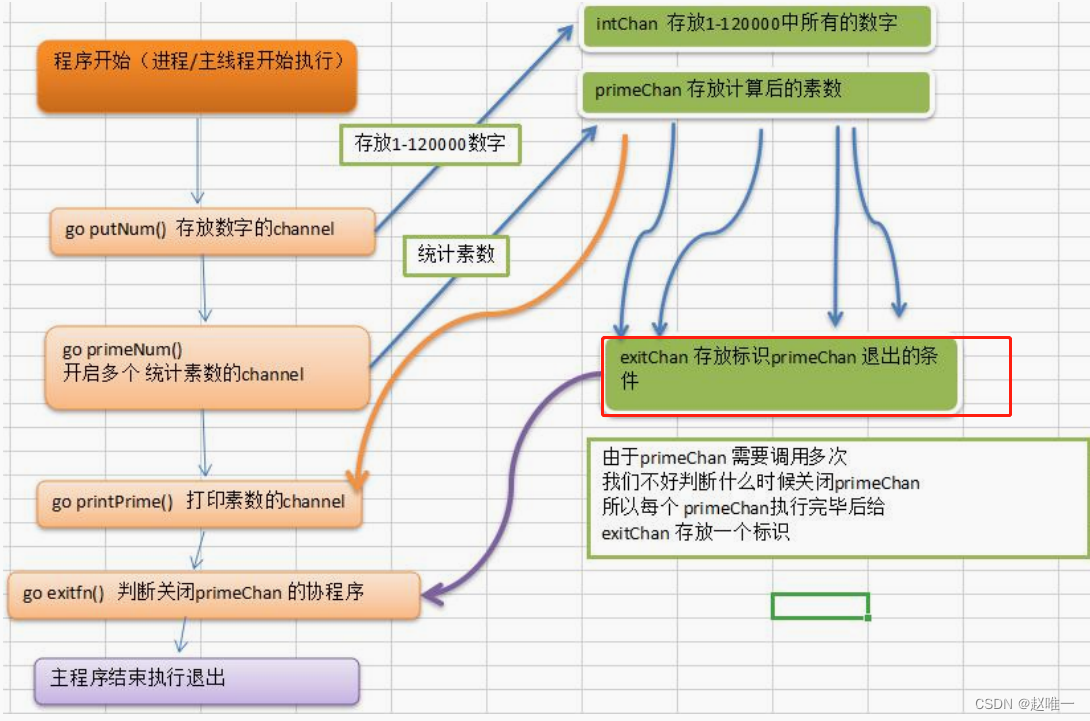
Golang协程,通道详解
进程、线程以及并行、并发 关于进程和线程 进程(Process)就是程序在操作系统中的一次执行过程,是系统进行资源分配和调度的基本单位,进程是一个动态概念,是程序在执行过程中分配和管理资源的基本单位,每一…...

unity 之 Vector 数据类型
文章目录 Vector 1Vector 2Vector 3Vector 4 Vector 1 在Unity中,Vector1 并不是一个常见的向量类型。 如果您需要表示标量(单个值)或者只需要一维的数据,通常会直接使用浮点数(float)或整数(in…...

私密数据采集:隧道爬虫IP技术的保密性能力探究
作为一名专业的爬虫程序员,今天要和大家分享一个关键的技术,它能够为私密数据采集提供保密性能力——隧道爬虫IP技术。如果你在进行敏感数据采集任务时需要保护数据的私密性,那么这项技术将是你的守护神。 在进行私密数据采集任务时ÿ…...

使用git rebase 之后的如何恢复到原始状态
我们常常喜欢使用git rebase去切换分支提交代码,操作流程就是: 先切换分支:比如当前是master 我们修改了一堆代码产生一个commit id :5555555567777 那么我们常常比较懒就直接切换了:git checkout dev 然后呢?使用命令git rebase 5555555567777,想把这笔修改提交到d…...

matlab相机标定知识整理
matlab相机标定知识整理 单目相机标定 单目相机标定 内参矩阵:cameraParams.Intrinsics.K 或者 cameraParams.K旋转矩阵:cameraParams.RotationMatrices 有待确定 cameraParams.RotationVectors平移矩阵:cameraParams.TranslationVectors径向…...

win11安装ubuntu 子系统安装过程及注意事项
第一步 :安装系统必须组件 由于子系统是系统自带组件,需要安装软件支持 第二步:应用商店安装 ubuntu 编辑 编辑 这个时候打开会报错 第三步,运行linux子系统 选择Windows PowerShell 以管理员身份运行) 输入&#…...
,dim=1)解析)
torch.cat((A,B),dim=1)解析
官方说明torch.cat 引用自:Pytorch中的torch.cat()函数 torch.cat(tensors, dim0, *, outNone) → Tensor # 连接给定维数的给定序列的序列张量。所有张量要么具有相同的形状(除了连接维度),要么为空。示例 输入: import torch a torch.Tens…...

apache配置安全证书https踩坑记录
apache配置安全证书有如下几步 一、申请证书 这个网上有很多免费的,我用的是阿里云的服务器,在阿里云后台就可以申请免费证书。 二、上传证书 申请好证书后,根据服务器用的什么软件,是apache还是ngnix,下载相应的证书…...
SQL Server Express 自动备份方案
文章目录 SQL Server Express 自动备份方案前言方案原理SQL Server Express 自动备份1.创建存储过程2.设定计划任务3.结果检查sqlcmd 参数说明SQL Server Express 自动备份方案 前言 对于许多小型企业和个人开发者来说,SQL Server Express是一个经济实惠且强大的数据库解决方…...

Docker资源控制
目录 一、CPU 资源控制 1.设置CPU使用率上限 2.设置CPU资源占用比(设置多个容器时才有效) 3.设置容器绑定指定的CPU 二、对内存使用的限制 三、对磁盘IO配额控制(blkio)的限制 一、CPU 资源控制 cgroups,是一个非常强…...
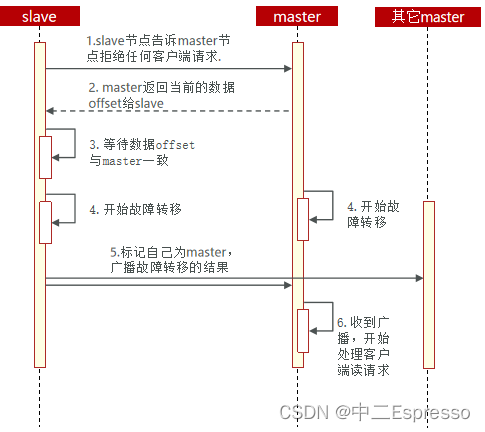
微服务中间件-分布式缓存Redis
分布式缓存 a.Redis持久化1) RDB持久化1.a) RDB持久化-原理 2) AOF持久化3) 两者对比 b.Redis主从1) 搭建主从架构2) 数据同步原理(全量同步)3) 数据同步原理(增量同步) c.Redis哨兵1) 哨兵的作用2) 搭建Redis哨兵集群3) RedisTem…...

java面试强基(16)
目录 clone方法的保护机制 Java中由SubString方法是否会引起内存泄漏? Java中提供了哪两种用于多态的机制? 程序计数器(线程私有) 如何判断对象是否是垃圾? clone方法的保护机制 clone0方法的保护机制在Object中是被声明为 protected的。以User…...
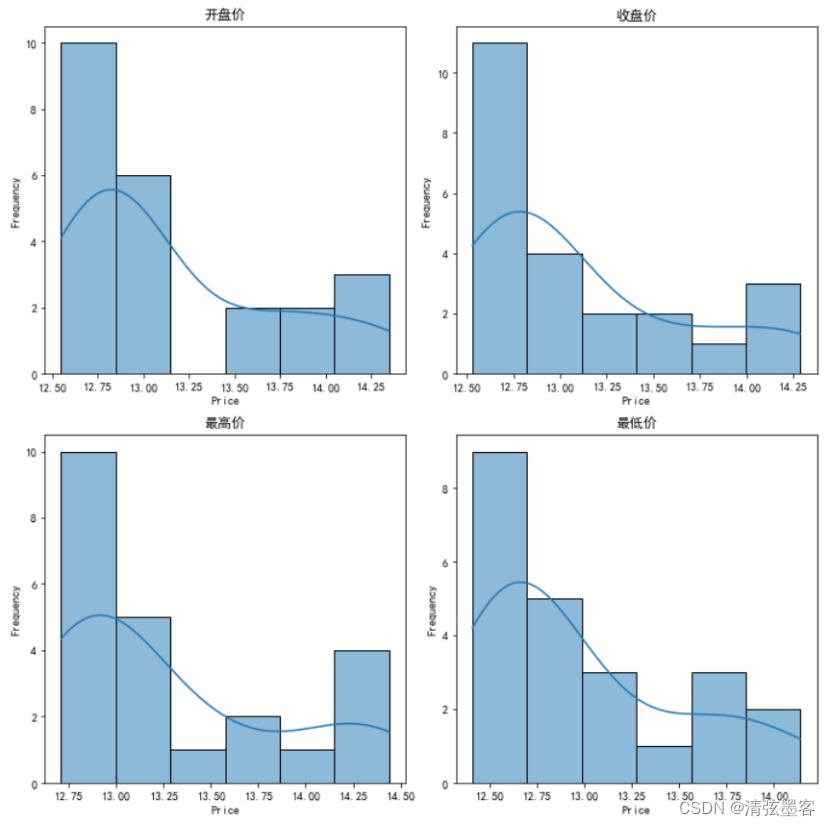
Python可视化在量化交易中的应用(13)_Seaborn直方图
Seaborn中带核密度的直方图的绘制方法 seaborn中绘制直方图使用的是sns.histlot()函数: sns.histplot(data,x,y,hue,weights,stat‘count’,bins‘auto’,binwidth,binrange,discrete,cumulative,common_bins,common_norm,multiple‘layer’,element‘bars’,fill,…...

NOIP 2006 普及组 第二题 开心的金明
开心的金明 说明 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。 更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超…...

「UG/NX」Block UI 指定点SpecifyPoint
✨博客主页何曾参静谧的博客📌文章专栏「UG/NX」BlockUI集合📚全部专栏「UG/NX」NX二次开发「UG/NX」BlockUI集合「VS」Visual Studio「QT」QT5程序设计「C/C+&#...

Linux Shell如果ping失败就重启网卡(详解)
直接上脚本 -------------------------------------------------------------------------- #vi /tmp/ping_check.sh #!/bin/bash IP="1.1.1.1" PacketLoss=`ping -c 4 -w 4 1.1.1.1 | grep packet loss | awk -F packet loss {print $1} | awk {print $NF}|se…...
每天一道leetcode:剑指 Offer 13. 机器人的运动范围(中等广度优先遍历剪枝)
今日份题目: 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0]的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之…...

TypeError: a bytes-like object is required, not ‘str‘
raceback (most recent call last): File "D:\pycharmcode\client.py", line 12, in <module> tcp_socket.send(send_data) TypeError: a bytes-like object is required, not str 使用socket进行ubuntu与windows通信时,发送数据时报了以上错…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...
