动态规划专题精讲1
致前行的人:
要努力,但不要着急,繁花锦簇,硕果累累都需要过程!

前言:
本篇文章为大家带来一种重要的算法题,就是动态规划类型相关的题目,动态规划类的题目在笔试和面试中是考察非常高频的一类,要想掌握这一类的题目就需要在掌握正确的学习方法的前提下做大量的练习,下面为大家介绍几道动态规划中比较经典的题目,每一道题目都有非常详细的思路实现,看完相信大家一定会有收获的!
1.动态规划概念:
动态规划,英⽂:Dynamic Programming,简称DP,如果某⼀问题有很多重叠⼦问题,使⽤动态规划是最有效的,动态规划中每⼀个状态⼀定是由上⼀个状态推导出来的
2.动态规划解题步骤
1. 确定dp数组(dp table)以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组
3.动态规划应该如何调试
找问题的最好⽅式就是把dp数组打印出来,看看究竟是不是按照⾃⼰思路推导的,做动规的题⽬,写代码之前⼀定要把状态转移在dp数组的上具体情况模拟⼀遍,⼼中有数,确定最后推出的是想要的结果。
然后再写代码,如果代码没通过就打印dp数组,看看是不是和⾃⼰预先推导的哪⾥不⼀样。如果打印出来和⾃⼰预先模拟推导是⼀样的,那么就是⾃⼰的递归公式、初始化或者遍历顺序有问题了。如果和⾃⼰预先模拟推导的不⼀样,那么就是代码实现细节有问题。
4.动态规划经典题目
斐波那契数 oj链接
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
思路:
按照动规五部曲依次推导
这⾥我们要⽤⼀个⼀维dp数组来保存递归的结果
1. 确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2. 确定递推公式
为什么这是⼀道⾮常简单的⼊门题⽬呢?
因为题⽬已经把递推公式直接给我们了:状态转移⽅程 dp[i] = dp[i - 1] + dp[i - 2];
3. dp数组如何初始化
题⽬中把如何初始化也直接给我们了,如下:
dp[0] = 0;
dp[1] = 1;
4. 确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍
历的顺序⼀定是从前到后遍历的
5. 举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导⼀下,当N为10的时候,dp数组应
该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是⼀致的。
以上我们⽤动规的⽅法分析完了,C++代码如下:
class Solution {
public:int fib(int n) {if(n <= 1)return n;vector<int> dp(n+1);dp[0] = 0;dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};时间复杂度:O(n)
空间复杂度:O(n)
爬楼梯oj链接
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
思路:
爬到第⼀层楼梯有⼀种⽅法,爬到⼆层楼梯有两种⽅法。那么第⼀层楼梯再跨两步就到第三层 ,第⼆层楼梯再跨⼀步就到第三层。
所以到第三层楼梯的状态可以由第⼆层楼梯 和 到第⼀层楼梯状态推导出来,那么就可以想到动态规划了。
动规五部曲:
定义⼀个⼀维数组来记录不同楼层的状态
1. 确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种⽅法
2. 确定递推公式
如果可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个⽅向推出来。
⾸先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种⽅法,那么再⼀步跳⼀个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种⽅法,那么再⼀步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候,⼀定要时刻想着dp[i]的定义,否则容易跑偏。这体现出确定dp数组以及下标的含义的重要性!
3. dp数组如何初始化
在回顾⼀下dp[i]的定义:爬到第i层楼梯,有dp[i]中⽅法。
那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但都基本是直接奔着答案去解释的。
例如强⾏安慰⾃⼰爬到第0层,也有⼀种⽅法,什么都不做也就是⼀种⽅法即:dp[0] = 1,相当于直接站在楼顶。
但总有点牵强的成分。
那还这么理解呢:我就认为跑到第0层,⽅法就是0啊,⼀步只能⾛⼀个台阶或者两个台阶,然⽽楼层是0,直接站楼顶上了,就是不⽤⽅法,dp[0]就应该是0.
其实这么争论下去没有意义,⼤部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1。
从dp数组定义的⾓度上来说,dp[0] = 0 也能说得通。
需要注意的是:题⽬中说了n是⼀个正整数,题⽬根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,这个初始化⼤家应该都没有争议的。
所以我的原则是:不考虑dp[0]如果初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4. 确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序⼀定是从前向后遍历的
5. 举例推导dp数组
举例当n为5的时候,dp table(dp数组)应该是这样的

如果代码出问题了,就把dp table 打印出来,看看究竟是不是和⾃⼰推导的⼀样。此时⼤家应该发现了,这不就是斐波那契数列么!唯⼀的区别是,没有讨论dp[0]应该是什么,因为dp[0]在本题没有意义!
以上五部分析完之后,C++代码如下:
class Solution {
public:int climbStairs(int n) {if(n <= 1)return n;vector<int> dp(n+1);dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};时间复杂度:O(n)
空间复杂度:O(n)
使用最小花费爬楼梯oj链接
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
思路:
使用动规五部曲:
1. 确定dp数组以及下标的含义
到达第i个台阶所花费的最少体⼒为dp[i]
2. 确定递推公式
题目描述中说,可以选择向上一次爬一个台阶或者一次爬两个台阶,所以到达第i阶台阶,可以通过第i-1阶台阶到达或者是通过第i-1阶台阶到达,然后在根据题目描述求的是达到顶楼所需要花费的最小体力,所以递推公式可以推导出:
dp[i] = min(dp[i-1]+cost[i-1] + dp[i-2]+cost[i-2])
3. dp数组如何初始化
题目描述说,可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯,也就是说到下标为0的台阶和到下标为1的台阶是不需要花费体力的,所以应该初始化为:
dp[0] = 0; dp[1] = 0;
4. 确定遍历顺序
本题的遍历顺序很简单,从前往后依次遍历就可以了
5.打印dp数组:

以上分析完毕,整体C++代码如下:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int>dp(cost.size()+1);dp[0] = 0;dp[1] = 0;for(int i = 2; i <= cost.size(); i++){dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};时间复杂度:O(n)
空间复杂度:O(n)
不同路径oj链接
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
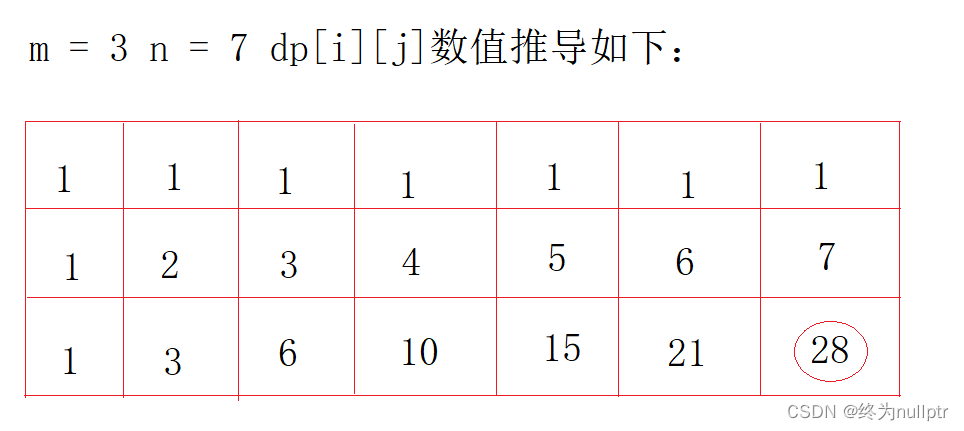
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:输入:m = 7, n = 3
输出:28
示例 4:输入:m = 3, n = 3
输出:6
思路:
机器⼈从(0 , 0) 位置触发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1. 确定dp数组以及下标的含义
dp[i][j] :表⽰从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2. 确定递推公式
根据题目中的描述机器人每次只能向下或者向右移动一步,所以到达dp[i][j]的路径总数是到达dp[i-1][j]的路径总数加上到达dp[i][j-1]的路径总数之和,所以递推公式应该为:dp[i][j] = dp[i-1][j] + dp[i][j-1]
3.dp数组的初始化
⾸先dp[i][0]⼀定都是1,因为从(0, 0)的位置到(i, 0)的路径只有⼀条,那么dp[0][j]也同理。
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;4. 确定遍历顺序
这⾥要看⼀下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上⽅和左⽅推导⽽来,那么从左到右⼀层⼀层遍历就可以了。
5. 举例推导dp数组
如图所示:
以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>>dp;dp.resize(m);for (int i = 0; i < dp.size(); i++){dp[i].resize(n, 0);}//初始化第一列:for (int i = 0; i < m; i++){dp[i][0] = 1;}//初始化第一行:for (int j = 0; j < n; j++){dp[0][j] = 1;}for (int i = 1; i < m; i++){for (int j = 1; j < n; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};时间复杂度:O(m * n)
空间复杂度:O(m * n)
不同路径2oj链接
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:
输入:obstacleGrid = [[0,1],[0,0]]
输出:1
思路:
通过动规五部曲来进行分析:
1. 确定dp数组(dp table)以及下标的含义
dp[i][j] :表⽰从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2. 确定递推公式
递推公式和62.不同路径⼀样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这⾥需要注意⼀点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}3. dp数组如何初始化
因为从(0, 0)的位置到(i, 0)的路径只有⼀条,所以dp[i][0]⼀定为1,dp[0][j]也同理。但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是⾛不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。

下标(0, j)的初始化情况同理。所以本题初始化代码为:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;注意代码⾥for循环的终⽌条件,⼀旦遇到obstacleGrid[i][0] == 1的情况就停⽌dp[i][0]的赋值1的操作,dp[0][j]同理
4. 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,⼀定是从左到右⼀层⼀层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]⼀定是有数值。
代码如下:
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}5. 举例推导dp数组

动规五部分分析完毕,对应C++代码如下:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>>dp;dp.resize(m);for(int i = 0; i < dp.size(); i++){dp[i].resize(n,0);}//初始化第一行:for(int i = 0; i < n; i++){if(obstacleGrid[0][i] == 1)break;dp[0][i] = 1; }//初始化第一列:for(int j = 0; j < m; j++){if(obstacleGrid[j][0] == 1)break;dp[j][0] = 1;}for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){if(obstacleGrid[i][j] == 1)continue;dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
};时间复杂度O(n * m) n m 分别为obstacleGrid 长度和宽度
空间复杂度O(n * m)
整数拆分oj链接
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
思路:
使用动规五部曲进行分析:
1. 确定dp数组(dp table)以及下标的含义
dp[i]:分拆数字i,可以得到的最⼤乘积为dp[i]。
2. 确定递推公式
可以想 dp[i]最⼤乘积是怎么得到的呢?其实可以从1遍历j,然后有两种渠道得到dp[i].
⼀个是j * (i - j) 直接相乘。
⼀个是j * dp[i - j],相当于是拆分(i - j)
那么从1遍历j,⽐较(i - j) * j和dp[i - j] * j 取最⼤的。
递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
3. dp的初始化
dp[0] dp[1]应该初始化多少呢?
有的题解⾥会给出dp[0] = 1,dp[1] = 1的初始化,但解释⽐较牵强,主要还是因为这么初始化可以把题⽬过了。
严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
拆分0和拆分1的最⼤乘积是多少?这是⽆解的。
这⾥我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最⼤乘积是1,这个没有任何异议!
4. 确定遍历顺序
确定遍历顺序,先来看看递归公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));dp[i] 是依靠 dp[i - j]的状态,所以遍历i⼀定是从前向后遍历,先有dp[i - j]再有dp[i]。枚举j的时候,是从1开始的。i是从3开始,这样dp[i - j]就是dp[2]正好可以通过我们初始化
的数值求出来。
所以遍历顺序为
for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}5. 举例推导dp数组
举例当n为10 的时候,dp数组⾥的数值,如下:

以上动规五部曲分析完毕,C++代码如下:
class Solution {
public:int integerBreak(int n){vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n; i++){for (int j = 1; j < i - 1; j++){dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));}}return dp[n];}
};时间复杂度:O(n^2)
空间复杂度:O(n)
不同的二叉搜索树oj链接
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3 输出:5示例 2:
输入:n = 1 输出:1
思路:
这道题⽬描述很简短,但估计⼤部分同学看完都是懵懵的状态,这得怎么统计呢?面对这道题,我们应该画画图,看看有没有什么规律

n为3,可以有5颗二叉搜索树:

来看看n为3的时候,有哪⼏种情况。
当1为头结点的时候,其右⼦树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是⼀样的啊!
(可能有同学问了,这布局不⼀样啊,节点数值都不⼀样。别忘了我们就是求不同树的数量,并不⽤把搜索树都列出来,所以不⽤关⼼其具体数值的差异)
当3为头结点的时候,其左⼦树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是⼀样的啊!
当2位头结点的时候,其左右⼦树都只有⼀个节点,布局是不是和n为1的时候只有⼀棵树的布局也是⼀样的啊!
发现到这⾥,其实我们就找到的重叠⼦问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种⽅式。
思考到这⾥,这道题⽬就有眉⽬了。
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右⼦树有2个元素的搜索树数量 * 左⼦树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右⼦树有1个元素的搜索树数量 * 左⼦树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右⼦树有0个元素的搜索树数量 * 左⼦树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
如图所示:

此时我们已经找到的递推关系了,那么可以⽤动规五部曲在系统分析⼀遍。
1. 确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的⼆叉搜索树的个数为dp[i]。
2. 确定递推公式
在上⾯的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左⼦树节点数量] *dp[以j为头结点右⼦树节点数量]
j相当于是头结点的元素,从1遍历到i为⽌。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左⼦树节点数量,i-j 为以j为头结点右⼦树节点数量
3. dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。那么dp[0]应该是多少呢?
从定义上来讲,空节点也是⼀颗⼆叉树,也是⼀颗⼆叉搜索树,这是可以说得通的。
4. 确定遍历顺序
⾸先⼀定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i⾥⾯每⼀个数作为头结点的状态,⽤j来遍历。
代码如下:
for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}
}5. 举例推导dp数组
n为5时候的dp数组状态如图:

综上分析完毕,C++代码如下:
class Solution {
public:int numTrees(int n) {vector<int>dp(n+1);dp[0] = 1;for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){dp[i] += dp[j-1]*dp[i-j];}}return dp[n];}
};时间复杂度O(n^2)
空间复杂度O(n)
相关文章:

动态规划专题精讲1
致前行的人: 要努力,但不要着急,繁花锦簇,硕果累累都需要过程! 前言: 本篇文章为大家带来一种重要的算法题,就是动态规划类型相关的题目,动态规划类的题目在笔试和面试中是考察非常高…...
PPO(proximal policy optimization)算法
博客写到一半发现有篇讲的很清楚,直接化缘了 https://www.jianshu.com/p/9f113adc0c50 Policy gradient 强化学习的目标:学习到一个策略πθ(a∣s)\pi\theta(a|s)πθ(a∣s)来最大化期望回报。 一种直接的方法就是在策略空间中直接搜索来得到最优策略&…...

ElasticSearch基本使用
title: ElasticSearch基本使用 date: 2022-08-29 00:00:00 tags: ElasticSearch基本使用 categories:ElasticSearch 基本概念 随着ES版本的升级,文中有些概念可能已经废弃。 索引词(term) 一个能够被索引的精确值,区分大小写,可以通过term查…...
windows微软商店下载应用失败/下载故障的解决办法;如何在网页上下载微软商店的应用
一、问题背景 设置惠普打印机时,需要安装hp smart,但是官方只提供微软商店这一下载渠道。 点击安装HP Smart,确定进入微软商店下载。 完全加载不出来,可能是因为开了代理。 把代理关了,就能正常打开了。 但是点击“…...
MySQL进阶篇之InnoDB存储引擎
06、InnoDB引擎 6.1、逻辑存储结构 表空间(Tablespace) 表空间在MySQL中最终会生成ibd文件,一个mysql实例可以对应多个表空间,用于存储记录、索引等数据。 段(Segment) 段,分为数据段&#x…...

商标侵权行为的种类有哪些
商标侵权行为的种类有哪些 1、商标侵权行为的种类有以下七种: (1)未经商标注册人的许可,在同一种商品上使用与其注册商标相同的商标的; (2)未经商标注册人的许可,在同一种商品上使用与其注册商标近似的商标,或者在类似商品上使…...
Similarity-Preserving KD(ICCV 2019)原理与代码解析
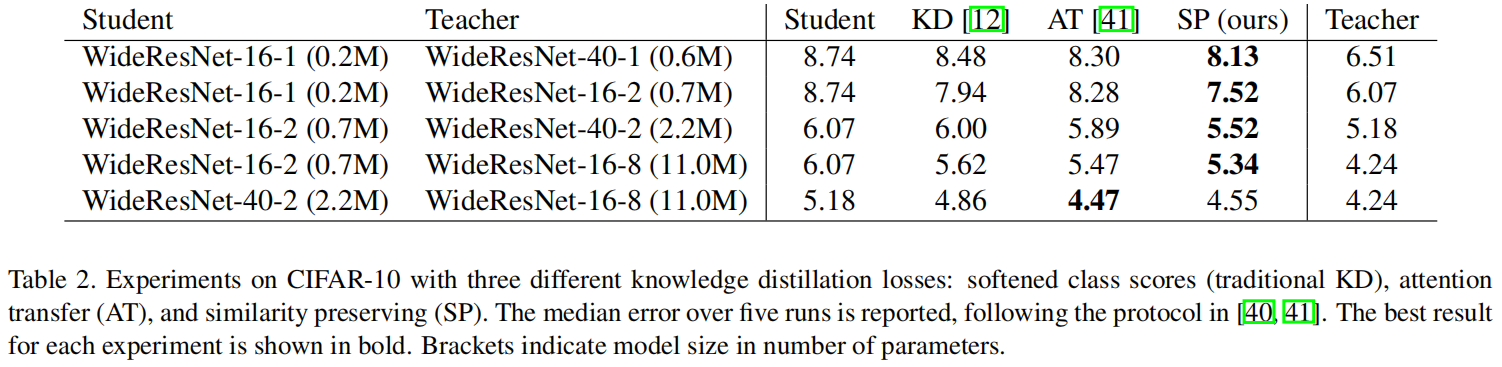
paper:Similarity-Preserving Knowledge Distillationcode:https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/SP.py背景本文的灵感来源于作者观察到在一个训练好的网络中,语义上相似的输入倾向于引起相似的…...
在Linux和Windows上安装seata-1.6.0
记录:381场景:在CentOS 7.9操作系统上,安装seata-1.6.0。在Windows上操作系统上,安装seata-1.6.0。Seata,一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。版本:JDK…...

兼职任务平台收集(二)分享给有需要的朋友们
互联网时代,给人们带来了很大的便利。信息交流、生活缴费、足不出户购物、便捷出行、线上医疗、线上教育等等很多。可以说,网络的时代会一直存在着。很多人也在互联网上赚到了第一桶金,这跟他们的努力和付出是息息相关的。所谓一份耕耘&#…...
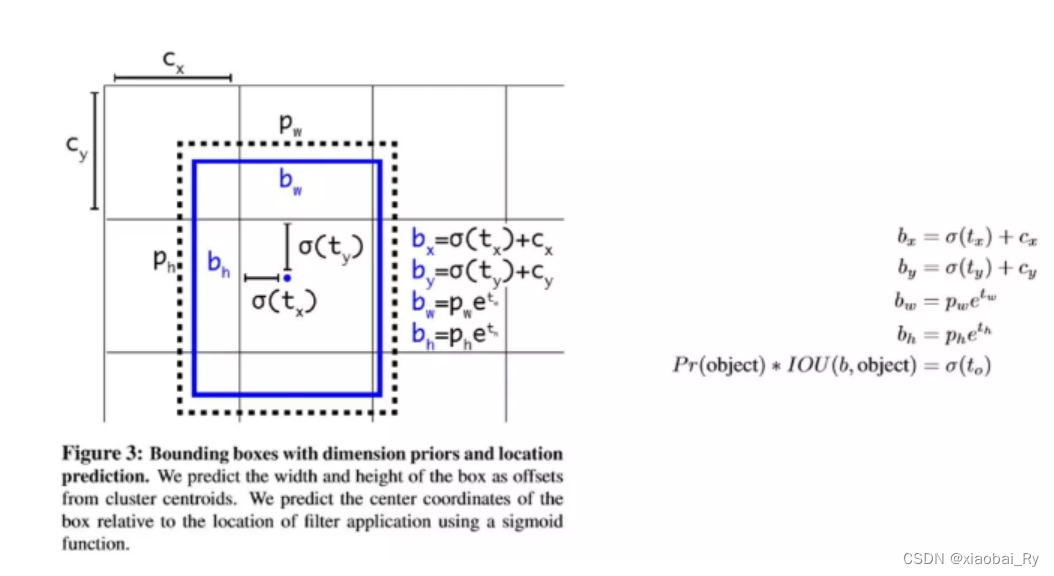
目标检测三大数据格式VOC,YOLO,COCO的详细介绍
注:本文仅供学习,未经同意请勿转载 说明:该博客来源于xiaobai_Ry:2020年3月笔记 对应的PDF下载链接在:待上传 目录 目标检测常见数据集总结 V0C数据集(Annotation的格式是xmI) A. 数据集包含种类: B. V0C2007和V0C2012的区别…...
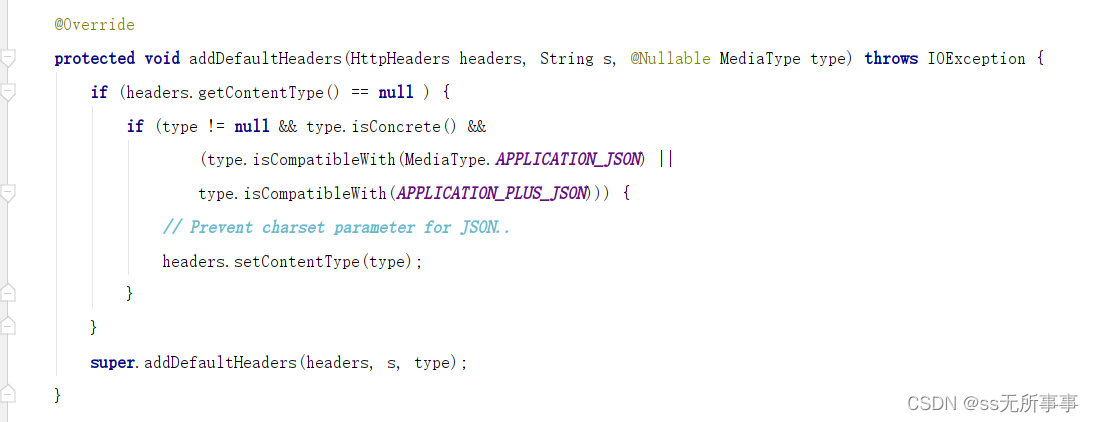
SpringBoot实现统一返回接口(除AOP)
起因 关于使用AOP去实现统一返回接口在之前的博客中我们已经实现了,但我突然突发奇想,SpringBoot中异常类的统一返回好像是通过RestControllerAdvice 这个注解去完成的,那我是否也可以通过这个注解去实现统一返回接口。 正文 这个方法主要…...

ChatGpt - 基于人工智能检索进行论文写作
摘要 ChatGPT 是一款由 OpenAI 训练的大型语言模型,可用于各种自然语言处理任务,包括论文写作。使用 ChatGPT 可以帮助作者提高论文的语言流畅度、增强表达能力和提高文章质量。在写作过程中,作者可以使用 ChatGPT 生成自然语言的段落、句子、单词或者短语,作为启发式的写…...

实例三:MATLAB APP design-多项式函数拟合
一、APP 界面设计展示 注:在左侧点击数据导入,选择自己的数据表,如果数据导入成功,在右侧的空白框就会显示数据导入成功。在多项式项数右侧框中输入项数,例如2、3、4等,点击计算按钮,右侧坐标框就会显示函数图像,在平均相对误差下面的空白框显示平均相对误差。...

springboot多种方式注入bean获取Bean
springboot动态注入bean1、创建Bean(demo)2、动态注入Bean3、通过注解注入Bean4、通过config配置注入Bean5、通过Import注解导入6、使用FactoryBean接口7、实现BeanDefinitionRegistryPostProcessor接口1、创建Bean(demo) Data public class Demo(){private String name;publi…...

Markdown及其语法详细介绍(全面)
文章目录一、基本语法1.标题2.段落和换行3.强调4.列表5.链接6.图片7.引用8.代码9.分割线10表格二、扩展语法1.标题锚点标题 {#anchor}2.脚注3.自动链接4.任务列表5.删除线6.表情符号7.数学公式三、Markdown 应用1.文档编辑2.博客写作3.代码笔记四、常见的工具和平台支持 Markdo…...
在Linux和Windows上安装sentinel-1.8.5
记录:380场景:在CentOS 7.9操作系统上,安装sentinel-1.8.5。在Windows上操作系统上,安装sentinel-1.8.5。Sentinel是面向分布式、多语言异构化服务架构的流量治理组件。版本:JDK 1.8 sentinel-1.8.5 CentOS 7.9官网地址…...
)
面试攻略,Java 基础面试 100 问(十)
StringBuffer、StringBuilder、String区别 线程安全 StringBuffer:线程安全,StringBuilder:线程不安全。 因为 StringBuffer 的所有公开方法都是 synchronized 修饰的,而 StringBuilder 并没有 synchronized 修饰。 StringBuf…...
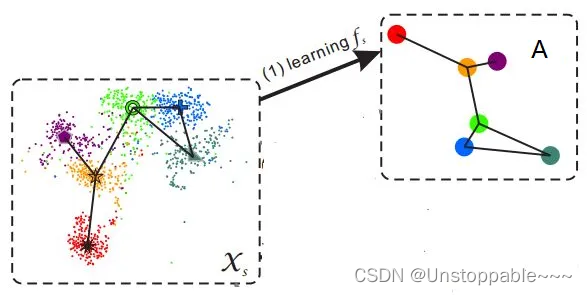
Zero-shot(零次学习)简介
zero-shot基本概念 首先通过一个例子来引入zero-shot的概念。假设我们已知驴子和马的形态特征,又已知老虎和鬣狗都是又相间条纹的动物,熊猫和企鹅是黑白相间的动物,再次的基础上,我们定义斑马是黑白条纹相间的马科动物。不看任何斑…...

51单片机简易电阻电感电容RLC测量仪仿真设计
51单片机简易电阻电感电容RLC测量仪仿真( proteus仿真程序讲解视频) 仿真图proteus7.8及以上 程序编译器:keil 4/keil 5 编程语言:C语言 设计编号:S0040 51单片机简易电阻电感电容RLC测量仪仿真51单片机最小系统的相关知识复位…...

[软件工程导论(第六版)]第6章 详细设计(课后习题详解)
文章目录1 假设只有SEQUENCE和DO-WHILE两种控制结构,怎样利用它们完成 IF THEN ELSE操作?2 假设只允许使用SEQUENCE和IF-THEN-ELSE两种控制结构,怎样利用它们完成DO WHILE操作?3 画出下列伪码程序的程序流程图和盒图:4…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...