二叉树OJ(一)二叉树的最大深度 二叉搜索树与双向链表 对称的二叉树
二叉树的最大深度
二叉树中和为某一值的路径(一)
二叉搜索树与双向链表
对称的二叉树
二叉树的最大深度
描述
求给定二叉树的最大深度,
深度是指树的根节点到任一叶子节点路径上节点的数量。
最大深度是所有叶子节点的深度的最大值。
(注:叶子节点是指没有子节点的节点。)
【递归】
class Solution {
public:int maxDepth(TreeNode* root) {// write code hereif(root==nullptr)return 0;int left = maxDepth(root->left);int right = maxDepth(root->right);return left>right?left+1:right+1;}
};【非递归】层序遍历(使用队列存储结点)
class Solution {
public:int maxDepth(TreeNode* root) {// write code hereif(root == nullptr)return 0;int res = 0;queue<TreeNode*> q;q.push(root);while(!q.empty()){int size = q.size();while(size--){TreeNode* cur = q.front();q.pop();if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}res++;}return res;}
};
二叉树中和为某一值的路径(一)
描述
给定一个二叉树root和一个值 sum ,判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点,不能从子节点到父节点
4.总节点数目为n
例如:
给出如下的二叉树, sum=22 sum=22,
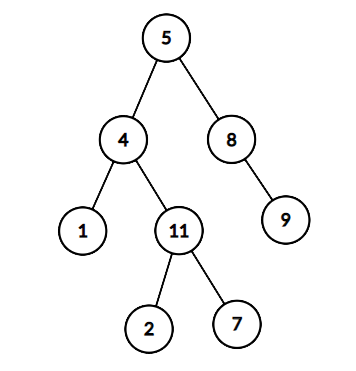
返回true,因为存在一条路径 5→4→11→25→4→11→2的节点值之和为 22
class Solution {
public:bool flag = false;void dfs(TreeNode* root, int sum){if(root==nullptr)return;sum-=root->val;if(sum==0 && root->left==nullptr && root->right==nullptr){flag = true; // 如果为根节点并且sum==0那么存在路径return;}dfs(root->left, sum);dfs(root->right, sum);}bool hasPathSum(TreeNode* root, int sum) {dfs(root, sum);return flag;}
};
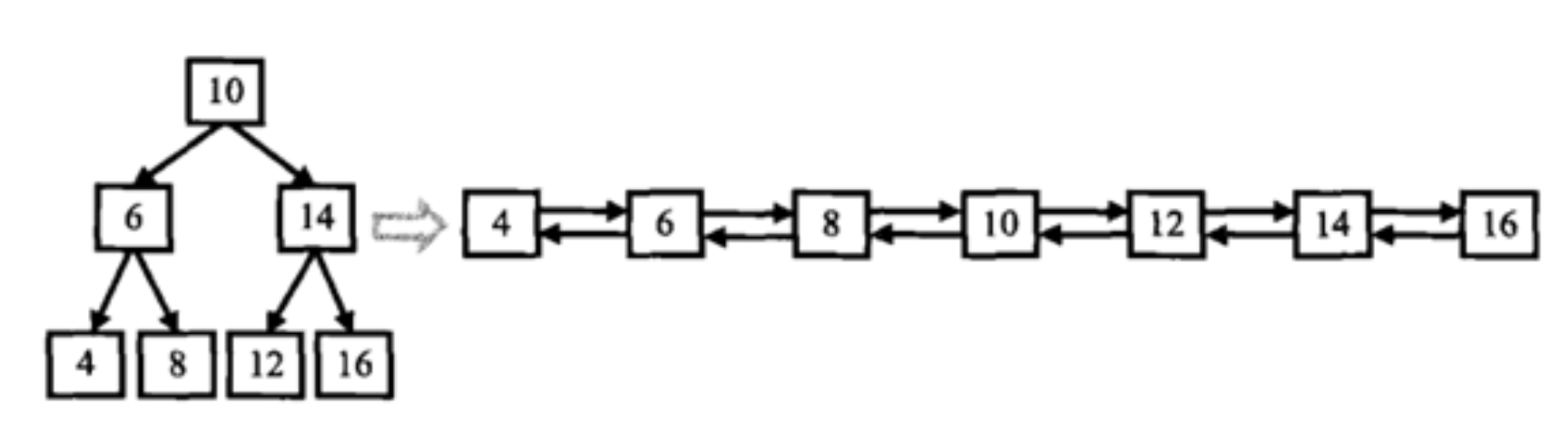
二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示
数据范围:输入二叉树的节点数 0≤n≤10000≤n≤1000,二叉树中每个节点的值 0≤val≤10000≤val≤1000
要求:空间复杂度O(1)O(1)(即在原树上操作),时间复杂度 O(n)O(n)注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构4.你不用输出双向链表,程序会根据你的返回值自动打印输出
class Solution {
public:vector<TreeNode*> res;void Inoder(TreeNode* root){if(root == NULL)return;Inoder(root->left);res.push_back(root);Inoder(root->right);}TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree==NULL)return NULL;Inoder(pRootOfTree);for(int i = 0; i < res.size()-1; ++i){res[i]->right = res[i+1];res[i+1]->left = res[i];}return res[0];}
};
对称的二叉树
描述
给定一棵二叉树,判断其是否是自身的镜像(即:是否对称)
例如: 下面这棵二叉树是对称的
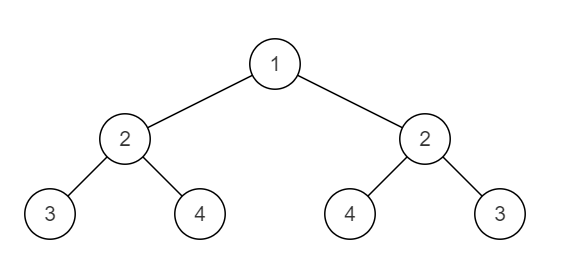
下面这棵二叉树不对称。
数据范围:节点数满足 0≤n≤10000≤n≤1000,节点上的值满足 ∣val∣≤1000∣val∣≤1000
要求:空间复杂度 O(n)O(n),时间复杂度 O(n)O(n)
备注:
你可以用递归和迭代两种方法解决这个问题
【递归解法】
class Solution {
public:bool recursion(TreeNode* p, TreeNode* q){if(p==nullptr && q==nullptr)return true;else if(p==nullptr || q==nullptr)return false;else if(q->val != p->val)return false;return recursion(p->left, q->right) && recursion(p->right, q->left);}bool isSymmetrical(TreeNode* root) {if(root==nullptr)return true;return recursion(root, root);}
};【非递归】
class Solution {
public:bool isSymmetrical(TreeNode* root) {if(root==nullptr)return true;queue<TreeNode*> q1;queue<TreeNode*> q2;q1.push(root->left);q2.push(root->right);while(!q1.empty() && !q2.empty()){TreeNode* left = q1.front();TreeNode* right = q2.front();q1.pop();q2.pop();if(left==nullptr && right==nullptr)continue;if(left==nullptr || right==nullptr || left->val != right->val)return false;q1.push(left->left);q1.push(left->right);q2.push(right->right);q2.push(right->left);}return true;}
};相关文章:

二叉树OJ(一)二叉树的最大深度 二叉搜索树与双向链表 对称的二叉树
二叉树的最大深度 二叉树中和为某一值的路径(一) 二叉搜索树与双向链表 对称的二叉树 二叉树的最大深度 描述 求给定二叉树的最大深度, 深度是指树的根节点到任一叶子节点路径上节点的数量。 最大深度是所有叶子节点的深度的最大值。 (注:…...

使用Fairseq进行Bart预训练
文章目录前言环境流程介绍数据部分分词部分预处理部分训练部分遇到的问题问题1可能遇到的问题问题1问题2前言 本文是使用 fairseq 做 Bart 预训练任务的踩坑记录huggingface没有提供 Bart 预训练的代码 facebookresearch/fairseq: Facebook AI Research Sequence-to-Sequence…...
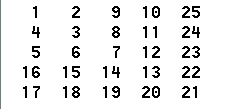
n阶数字回转方阵 ← 模拟法
【问题描述】 请编程输出如下数字回旋方阵。 【算法代码】 #include <bits/stdc.h> using namespace std;const int maxn100; int z[maxn][maxn];void matrix(int n) {int num2;z[0][0]1;int i0,j1;while(i<n && j<n) {while(i<j) z[i][j]num;while(j&…...

【人工智能AI】二、NoSQL 基础知识《NoSQL 企业级基础入门与进阶实战》
写一篇介绍 NoSQL 基础知识的技术文章,分5个章节,每个章节细分到3级目录,重点介绍一下NoSQL 数据模型,NoSQL 数据库架构,NoSQL 数据库特性等,不少于2000字。 NoSQL 基础知识 NoSQL(Not Only SQ…...

Camera Rolling Shutter和Global Shutter的区别
卷帘快门(Rolling Shutter)与全局快门(Global Shutter)的区别 什么是快门 快门是照相机用来控制感光片有效曝光时间的机构。 快门是照相机的一个重要组成部分,它的结构、形式及功能是衡量照相机档次的一个重要因素。 …...

模版之AnyType
title: 模版之AnyType date: 2023-02-19 21:49:53 permalink: /pages/54a0bf/ categories: 通用领域编程语言C tags:C元编程 author: name: zhengzhibing link: https://azmddy.top/pages/54a0bf/ 模版之AnyType 在研究C的编译期反射时,发现了AnyType很有意思。 首…...

【汇编】一、环境搭建(一只 Assember 的成长史)
嗨~你好呀! 我是一名初二学生,热爱计算机,码龄两年。最近开始学习汇编,希望通过 Blog 的形式记录下自己的学习过程,也和更多人分享。 这篇文章主要讲述汇编环境的搭建过程。 话不多说~我们开始吧! 系统环…...

【博客628】k8s pod访问集群外域名原理以及主机开启了systemd-resolved的不同情况
k8s pod访问集群外域名原理以及使用了systemd-resolved的不同情况 1、不同情况下的linux主机访问外部域名原理 没有使用systemd-resolved的linux主机上访问外部域名一般是按照以下步骤来的: 从dns缓存里查找域名与ip的映射关系 从/etc/hosts里查找域名与ip的映射…...

测试3.测试方法的分类
3.测试分类 系统测试包括回归测试和冒烟测试 回归测试:修改了旧的代码后,重新测试功能是否正确,有没有引入新的错误或导致其它代码产生错误 冒烟测试:目的是确认软件基本功能正常,可以进行后续的正式测试工作 按是否…...
Android 基础知识4-2.9 FrameLayout(帧布局)详解
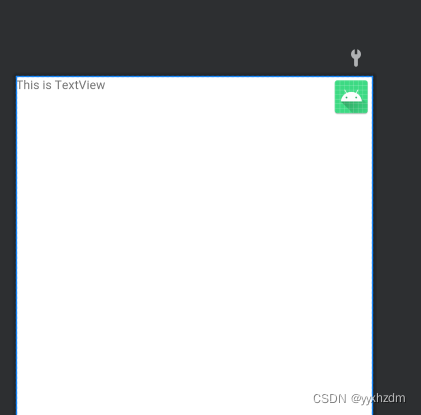
一、FrameLayout(帧布局)概述 FrameLayout又称作帧布局,它相比于LinearLayout和RelativeLayout要简单很多,因为它的应用场景也少了很多。这种布局没有方便的定位方式,所有的控件都会默认摆放在布局的左上角。 示例1代…...

Go语言xorm框架
xorm xorm是一个简单而强大的Go语言ORM库通过它可以使数据库操作非常简便。 官网: https://xorm.io/ 中文文档: https://gitea.com/xorm/xorm/src/branch/master/README_CN.md 特性 支持 Struct 和数据库表之间的灵活映射,并支持自动同步事务支持同时支持原始SQL…...

19_微信小程序之优雅实现侧滑菜单
19_微信小程序之优雅实现侧滑菜单一.先上效果图 要实现这样一个效果,布局其实很简单,整体布局是一个横向滚动的scroll-view,难点在于怎么控制侧滑菜单的回弹,以及寻找回弹的边界条件? 此篇文章主要是基于uni-app来实现的…...

JSP中JDBC与javaBean学习笔记
本博文源于博主偷偷复习期末的java web,博文主要讲述JDBC API与JavaBean,涉及driver,driver Manager\connection、statement接口、PreparedStatement接口、ResultSet接口,JavaBean包含一些标记介绍。 1.JDBC API JDBC由一组接口和类组成&am…...

编译Android系统源码推荐的电脑配置
工欲善其事,必先利其器。 看到很多客户,搞Android产品开发,用的电脑配置是惨不忍睹。 这些老板脑子有坑吗... ------------ 编译Android9推荐电脑配置: 处理器:酷睿i7 5代系列 8线程以上 内存: 8GB以上…...

加油站会员管理小程序实战开发教程10
上一篇我们介绍了计算距离及到店导航的功能,本篇我们介绍一下今日油价的功能。 如果要按日显示最新的数据,那么我们首先需要有数据源来存放每日的油价数据。这里涉及数据源的时候要考虑你的数据是只录入一条,还是每日录入一条。 录入一条呢,比较简单,但有个问题是如果我…...

shell编程之条件判断和流程控制
typora-copy-images-to: pictures typora-root-url: …\pictures 文章目录typora-copy-images-to: pictures typora-root-url: ..\..\pictures本节课程目标一、条件判断语法结构2. 条件判断相关参数㈠ 判断文件类型㈡ 判断文件权限㈢ 判断文件新旧㈣ 判断整数㈤ 判断字符串㈥ 多…...

第一次接触jquery
文章目录一.关于jqurey二.什么是jqurey三.上课实例1.表格 2.鼠标移动效果 3隐藏和显示效果代码如下注意一.关于jqurey 简而言之:jQuery 是一个 JavaScript 库。 jQuery 极大地简化了 JavaScript 编程。 二.什么是jqurey jQuery 是一个 JavaScript 函数库。 jQu…...

Vue中 引入使用 babel-polyfill 兼容低版本浏览器
注意:本文主要介绍的 vue-cli 版本:3.x, 4.x; 最近在项目中使用 webpack 打包后升级,用户反馈使用浏览器(chrome 45)访问白屏。经过排查发现:由于 chrome 45 无法兼容 ES6 语法导致的…...
ArcGIS Enterprise on Kubernetes 11.0安装示例
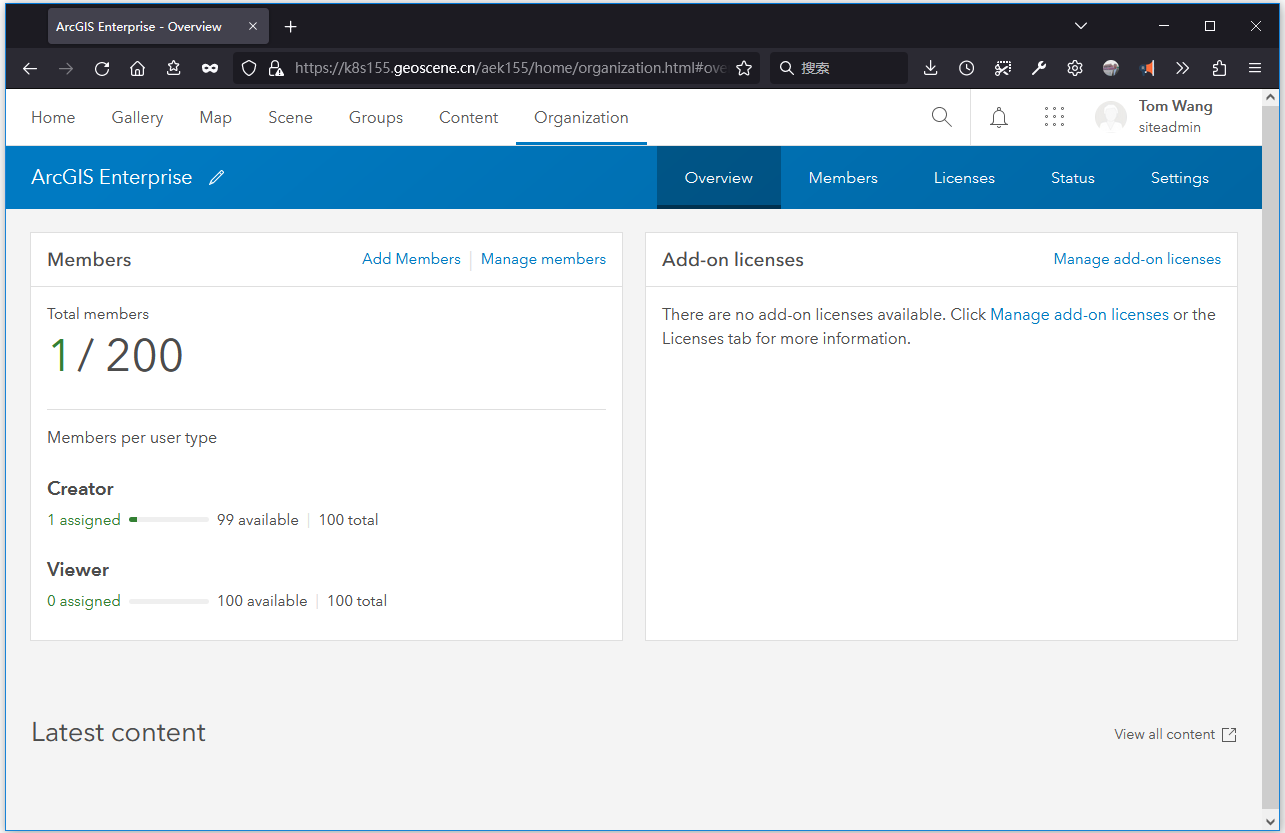
博客主页:https://tomcat.blog.csdn.net 博主昵称:农民工老王 主要领域:Java、Linux、K8S 期待大家的关注💖点赞👍收藏⭐留言💬 目录安装前置条件基本安装解压文件生成秘钥执行安装脚本配置DNS方法一方法二…...
js 防抖函数 节流函数
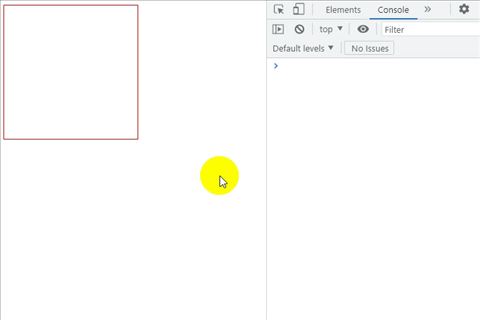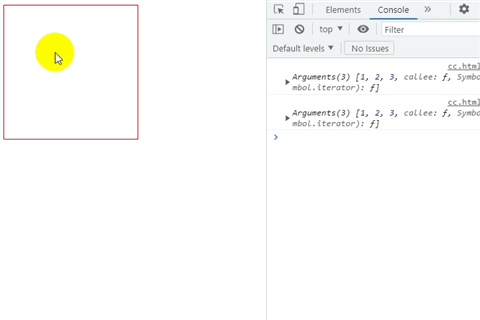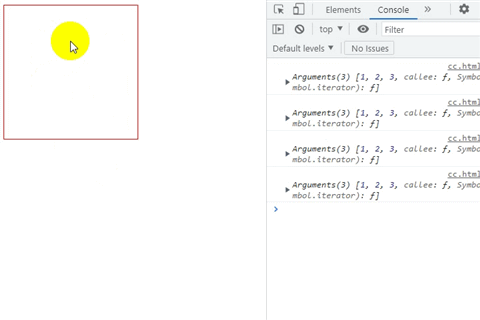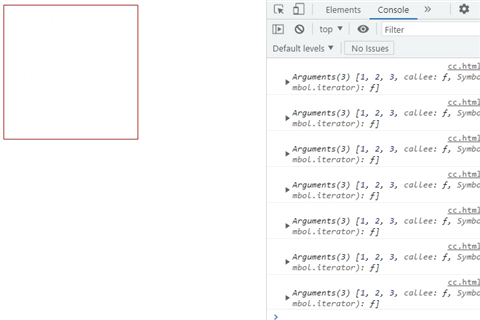
某些事件中(如 onresize onscroll onkeydown onkeyup onmousemove …),会连续触发函数的执行,如果函数执行一些耗时的操作(如请求数据…),会影响性能,也有可能造成服务器压力。这时可以用 防抖函数 或 节流函数解决这种问题。 防…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...