第四章,向量组,2-矩阵等价与向量组等价的关系
第四章,向量组,2-矩阵等价与向量组等价的关系
- 矩阵乘法与线性表示
- 矩阵等价与向量组等价
玩转线性代数(23)线性组合与线性表示的应用的笔记,相关证明以及例子见原文
矩阵乘法与线性表示
设有 A m ∗ n B n ∗ l = C m ∗ l A_{m*n}B_{n*l}=C_{m*l} Am∗nBn∗l=Cm∗l,那么A、B矩阵的行、列向量组与C的行、列向量组之间有什么关系呢?
先看C的行向量组, C = A B C=AB C=AB,根据初等变换的知识,A在B左边,说明是对B进行的行变换(此时的行变换不一定是初等行变换,也不一定是可逆的),将B的行变成了C的行,故C的行向量组可以由B的行向量组来线性表示,如下:
( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ) ( b 1 T b 2 T ⋮ b n T ) = ( c 1 T c 2 T ⋮ c m T ) \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \begin{pmatrix} b_1^T\\ b_2^T\\ \vdots \\ b_n^T\\ \end{pmatrix}=\begin{pmatrix} c_1^T\\ c_2^T\\ \vdots \\ c_m^T\\ \end{pmatrix} a11a21⋮am1a12a22⋮am2⋯⋯⋮⋯a1na2n⋮amn b1Tb2T⋮bnT = c1Tc2T⋮cmT
同理,C的列向量组可由A的列向量组线性表示
( c 1 c 2 ⋯ c l ) = ( a 1 a 2 ⋯ a n ) ( b 11 b 12 ⋯ b 1 n b 21 b 22 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ b n 1 b n 2 ⋯ b n l ) \begin{pmatrix} c_1 & c_2 & \cdots & c_l \end{pmatrix}= \begin{pmatrix} a_1 & a_2 & \cdots & a_n \end{pmatrix} \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nl} \\ \end{pmatrix} (c1c2⋯cl)=(a1a2⋯an) b11b21⋮bn1b12b22⋮bn2⋯⋯⋮⋯b1nb2n⋮bnl
矩阵等价与向量组等价
矩阵等价是两个矩阵可经过初等变换来相互转化;两个向量组等价是指它们可以相互线性表示。两个向量组等价的判断条件也已经清楚,就是 R ( A ) = R ( B ) = R ( A , B ) R(A)=R(B)=R(A,B) R(A)=R(B)=R(A,B)
矩阵等价有行等价、列等价和等价有一种形式,如何判断两个矩阵等价?首先矩阵是同型矩阵,其次矩阵A与B的秩相等。因为若 R ( A ) = R ( B ) R(A)=R(B) R(A)=R(B),则A与B的标准形是相同的,即
A ∼ F = ( E r 0 0 0 ) A\sim F=\begin{pmatrix} E_r & 0\\ 0 & 0 \end{pmatrix} A∼F=(Er000),同时 B ∼ F = ( E r 0 0 0 ) B\sim F=\begin{pmatrix} E_r & 0\\ 0 & 0 \end{pmatrix} B∼F=(Er000)
根据等价矩阵的传递性知, A ∼ B A\sim B A∼B。
由此可知,对两个向量组 A : a 1 , a 2 , ⋯ , a m , B : b 1 , b 2 , ⋯ , b l A:a_1,a_2,\cdots,a_m, B:b_1,b_2,\cdots,b_l A:a1,a2,⋯,am,B:b1,b2,⋯,bl和两个矩阵 A = ( a 1 , a 2 , ⋯ , a m ) , B : ( b 1 , b 2 , ⋯ , b l ) A=(a_1,a_2,\cdots,a_m), B:(b_1,b_2,\cdots,b_l) A=(a1,a2,⋯,am),B:(b1,b2,⋯,bl),向量组A与B等价 ⇒ \Rightarrow ⇒矩阵A与B等价,反之不成立。
若矩阵A与B等价,可以推出的结论:
(1)若 A ∼ r B A^r_{\sim}B A∼rB,则存在可逆矩阵P,使PA=B,即B=PA,所以B的行向量组可由A的行向量组线性表示,同时有 A = P − 1 B A=P^{-1}B A=P−1B,所以A的行向量组也可以由B的行向量组线性表示,说明A与B的行向量组等价;
(2)若 A ∼ c B A^c_{\sim}B A∼cB,A与B的列向量组是等价的。
其实线性表示与线性组合这些概念也可以用到方程组上.对方程组A的各个方程作线性运算所得到的一个方程就称为方程组A的一个线性组合;若其中一个方程可以写成其它方程的线性组合,则称该方程可由其它方程线性表示,若方程组B的每个方程都可由方程组A的线性表示,就称方程组B能由方程组A线性表示,这时方程组A 的解一定是方程组B的解;若方程组A与方程组B能相互线性表示,就称这两个方程组等价,等价的方程组一定同解
为什么方程组B能由方程组A线性表示,方程组A 的解一定是方程组B的解?
理解:方程组B能由方程组A线性表示,即若 x ∈ A x\in A x∈A一定有 x ∈ B x\in B x∈B,所以A的解都是B的解,B的解集合范围大。
相关文章:

第四章,向量组,2-矩阵等价与向量组等价的关系
第四章,向量组,2-矩阵等价与向量组等价的关系 矩阵乘法与线性表示矩阵等价与向量组等价 玩转线性代数(23)线性组合与线性表示的应用的笔记,相关证明以及例子见原文 矩阵乘法与线性表示 设有 A m ∗ n B n ∗ l C m ∗ l A_{m*n}B_{n*l}C_{m…...
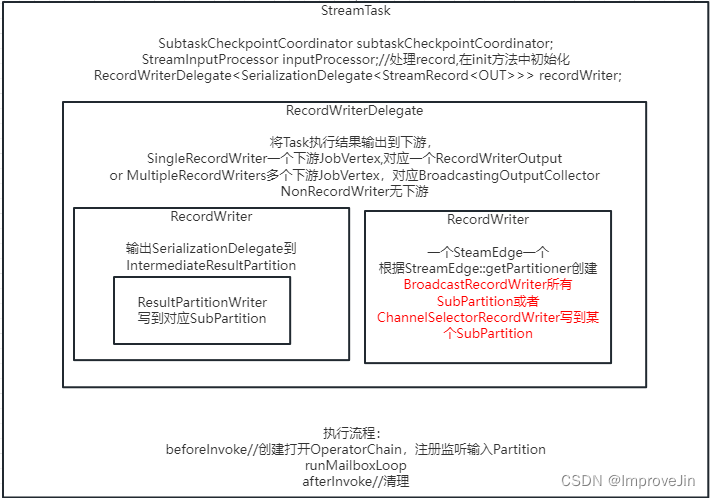
Flink源码之StreamTask启动流程
每个ExecutionVertex分配Slot后,JobMaster就会向Slot所在的TaskExecutor提交RPC请求执行Task,接口为TaskExecutorGateway::submitTask CompletableFuture<Acknowledge> submitTask(TaskDeploymentDescriptor tdd, JobMasterId jobMasterId, RpcTi…...
)
【BASH】回顾与知识点梳理(三十)
【BASH】回顾与知识点梳理 三十 三十. 进程的观察30.1 ps :将某个时间点的进程运作情况撷取下来仅观察自己的 bash 相关进程: ps -l观察系统所有进程: ps aux 30.2 top:动态观察进程的变化30.3 pstree 该系列目录 --> 【BASH】…...
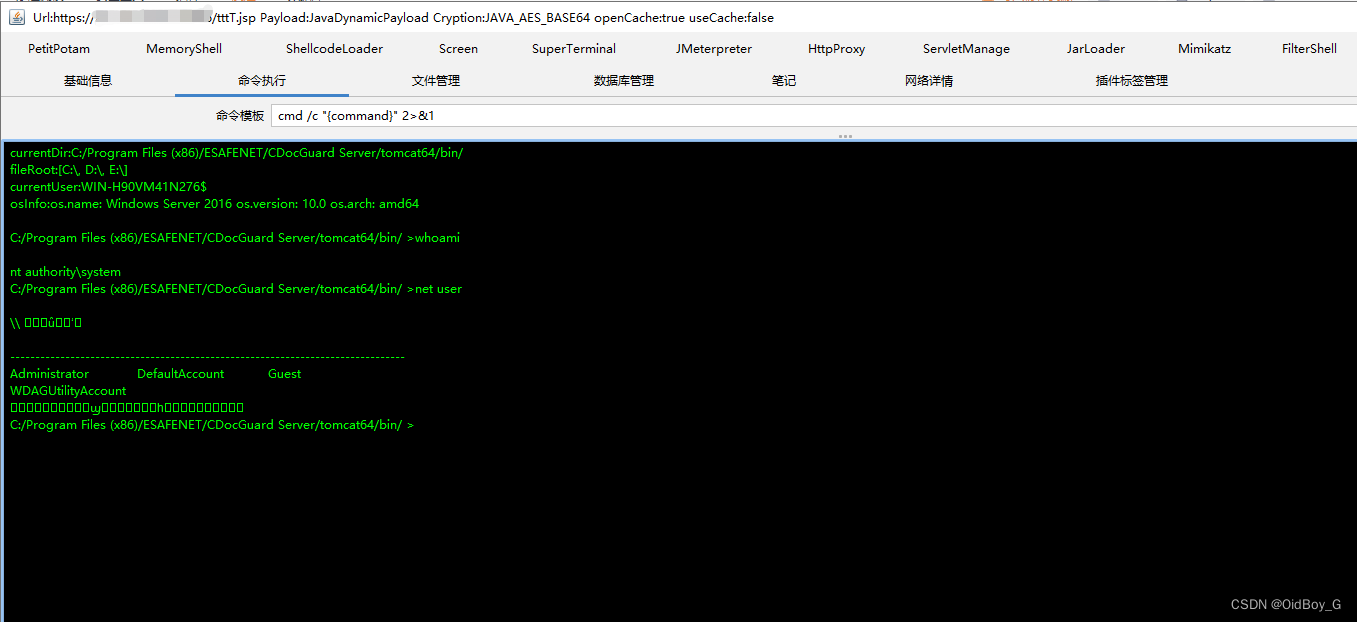
亿赛通电子文档安全管理系统任意文件上传漏洞复现
0x01 产品简介 亿赛通电子文档安全管理系统(简称:CDG)是一款电子文档安全加密软件,该系统利用驱动层透明加密技术,通过对电子文档的加密保护,防止内部员工泄密和外部人员非法窃取企业核心重要数据资产&…...
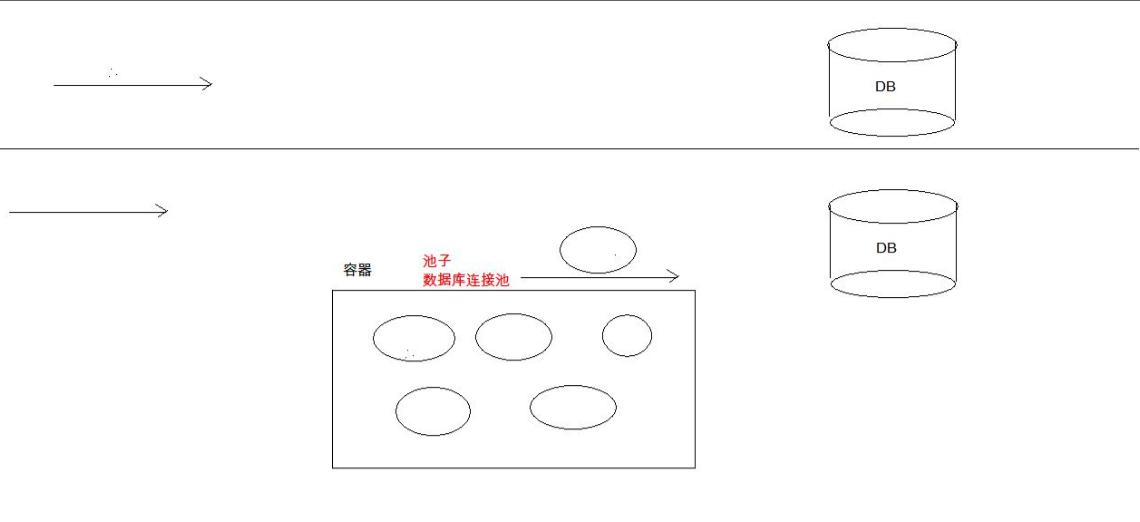
java:数据库连接池
概念 举个例子来说吧,假设我们开了一家餐馆,客人来了,我们就请一个服务员,使用完后再把他开除了,下个客人再来了,我们再请一个,使用完再开除。 这是不是我们现在使用 JDBC 连接数据库的场景&a…...
-条形图(一))
可视化绘图技巧100篇基础篇(三)-条形图(一)
目录 前言 适用场景 图例 条形图分类 多系列条形图 单系列条形图...
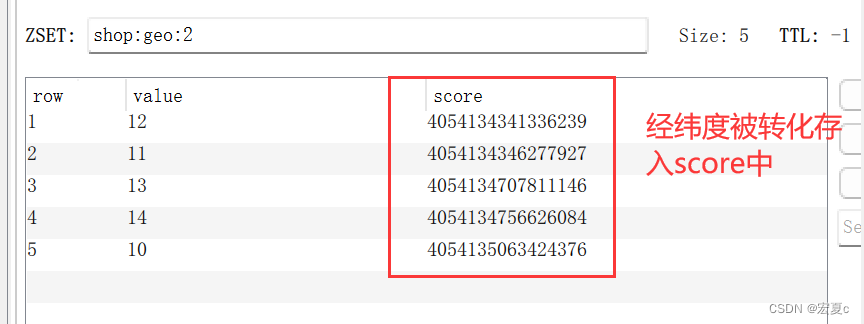
如何使用Redis实现附近商家查询
导读 在日常生活中,我们经常能看见查询附近商家的功能。 常见的场景有,比如你在点外卖的时候,就可能需要按照距离查询附近几百米或者几公里的商家。 本文将介绍如何使用Redis实现按照距离查询附近商户的功能,并以SpringBoot项目…...
于vue3+vite+element pro + pnpm开源项目
河码桌面是一个基于vue3viteelement pro pnpm 创建的monorepo项目,项目采用的是类操作系统的web界面,操作起来简单又方便,符合用户习惯,又没有操作系统的复杂! 有两个两个分支,一个是web版本,…...
18-组件化开发 根组件
组件化开发 & 根组件: 1. 组件化:一个页面可以拆分成一个个组件,每个组件有着自己独立的结构、样式、行为. 好处:便于维护,利于复用->提升开发效率 组件分类: 普通组件 , 根组件 2. 根组件:整个应用最上层的组件,包裹所有普通小组件…...

springboot集成ES
1.引入pom依赖2.application 配置3.JavaBean配置以及ES相关注解 3.1 Student实体类3.2 Teacher实体类3.3 Headmaster 实体类4. 启动类配置5.elasticsearchRestTemplate 新增 5.1 createIndex && putMapping 创建索引及映射 5.1.1 Controller层5.1.2 service层5.1.3 ser…...

Maven 生成编译时间和版本Java类
本文使用Maven插件来自动生成一个 Version.java 类,可以在Java代码中使用里面对应的常量,获取当前版本号和构建时间。 Maven编译后自动生成的 Version.java 文件内容如下所示: package com.shanhy.demo;public final class Version {public…...

关于uniapp微信小程序scroll-view组件使用show-scrollbar隐藏不了滚动条
这里关于使用 scroll-view组件 时候有滚动条 想要隐藏滚动条但是使用show-scrollbar没有效果 这时候又使用类名隐藏滚动条 使用id隐藏滚动条都不行 解决方法:在使用 scroll-view组件 的页面或者app 页面加上以下代码就可以了 ::-webkit-scrollbar {displa…...

CSS:filter滤镜 详解(用法 + 代码 + 例子 + 效果)
文章目录 filter 滤镜blur() 模糊度例子 渐变光晕 brightness() 元素亮度contrast() 对比度grayscale() 元素灰度hue-rorate() 色相opacity() 透明度invert() 反转颜色saturate() 饱和度 backdrop-filter 蒙版,滤镜例子 卷轴展开 filter 滤镜 动图为效果添加前后对…...

【Unity每日一记】Physics.Raycast 相关_Unity中的“X光射线”
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...
软件报错msvcr90.dll丢失的解决方法,亲测可以修复
我曾经遇到过一个令人头疼的问题:msvcr90.dll丢失。这个问题导致了我的程序无法正常运行,让我感到非常苦恼。然而,在经过一番努力后,我终于成功地修复了这个问题,这让我感到非常欣慰和满足。 msvcr90.dll丢失的原因可能…...

第一百一十八回 如何获取蓝牙连接状态
文章目录 知识回顾实现方法示例代码我们在上一章回中介绍了如何连接蓝牙设备相关的内容,本章回中将介绍如何获取蓝牙连接状态.闲话休提,让我们一起Talk Flutter吧。 知识回顾 我们在上一章回中介绍如何连接蓝牙设备,但是如何知道蓝牙设备是否连接成功呢?这就需要我们去获取…...
 windows临界区、其他各种mutex互斥量)
C++11并发与多线程笔记(12) windows临界区、其他各种mutex互斥量
C11并发与多线程笔记(12) windows临界区、其他各种mutex互斥量 1、windows临界区2、自动析构技术3、递归独占互斥量 std::recursive_mutex4、带超时的互斥量 std::timed_mutex 和 std::recursive_timed_mutex4.1 std::timed_mutex:是带超时的…...
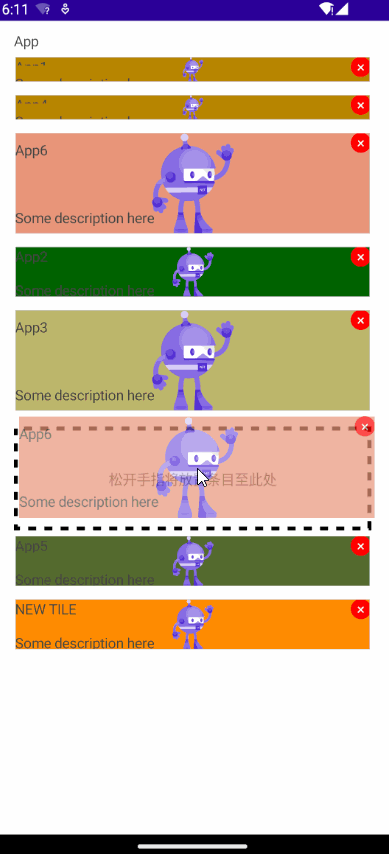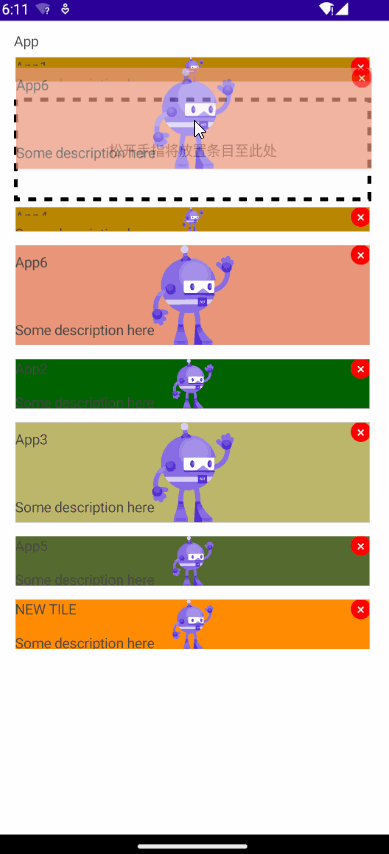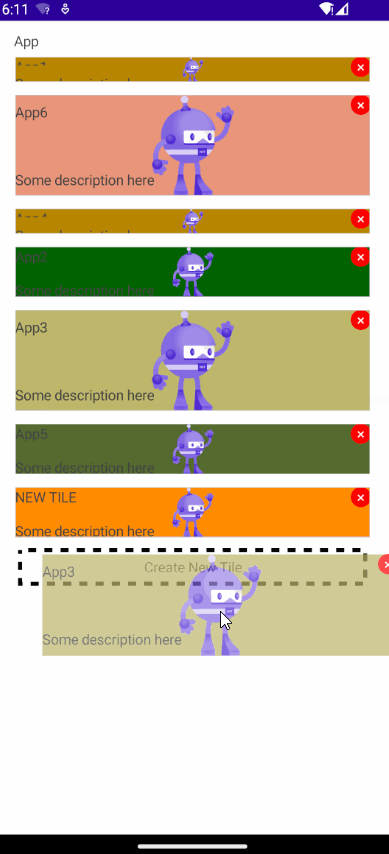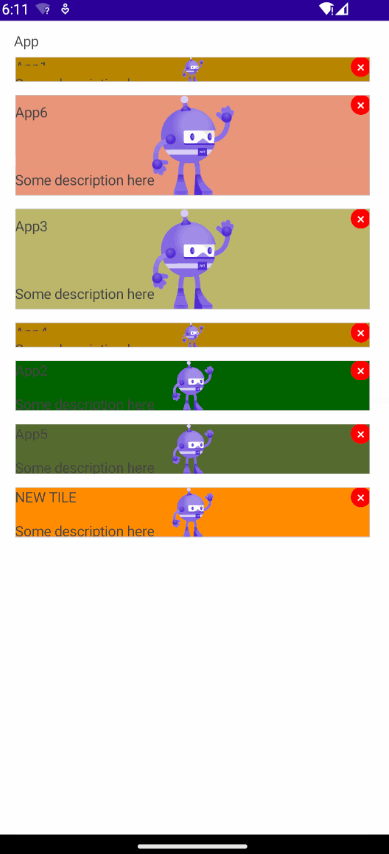
[MAUI]在.NET MAUI中实现可拖拽排序列表
文章目录 创建可拖放控件创建绑定服务类拖拽(Drag)拖拽悬停,经过(DragOver)释放(Drop) 创建页面元素最终效果项目地址 .NET MAUI 中提供了拖放(drag-drop)手势识别器,允许用户通过拖…...

Linux 内核内存管理 pfn_to_online_page宏
文章目录 一、Memory Hotplug1.1 简介1.2 热插拔事件通知机制 二、pfn_to_online_page2.1 pfn_to_online_page2.2 pfn_to_section_nr2.3 online_section_nr 参考资料 一、Memory Hotplug 1.1 简介 Linux 内存热插拔(Memory Hotplug)是指在运行时动态增…...

『C语言初阶』第八章 -结构体
前言 今天小羊又来给铁汁们分享关于C语言的结构体,在C语言中,结构体类型属于一种构造类型(其他的构造类型还有:数组类型,联合类型),今天我们主要简单了解一下结构体。 一、结构体是什么&#x…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
