【考研数学】概率论与数理统计 | 第一章——随机事件与概率(2,概率基本公式与事件独立)
文章目录
- 引言
- 四、概率基本公式
- 4.1 减法公式
- 4.2 加法公式
- 4.3 条件概率公式
- 4.4 乘法公式
- 五、事件的独立性
- 5.1 事件独立的定义
- 5.1.1 两个事件的独立
- 5.1.2 三个事件的独立
- 5.2 事件独立的性质
- 写在最后
引言
承接上文,继续介绍概率论与数理统计第一章的内容。
四、概率基本公式
4.1 减法公式
P ( A − B ) = P ( A B ‾ ) = P ( A ) − P ( A B ) . P(A-B)=P(A \overline{B} )=P(A)-P(AB). P(A−B)=P(AB)=P(A)−P(AB). 证明: A = ( A − B ) + A B A=(A-B)+AB A=(A−B)+AB ,且 A − B A-B A−B 与 A B AB AB 互斥,根据概率的有限可加性,有 P ( A ) = P ( A − B ) + P ( A B ) P(A)=P(A-B)+P(AB) P(A)=P(A−B)+P(AB) ,即 P ( A − B ) = P ( A ) − P ( A B ) P(A-B)=P(A)-P(AB) P(A−B)=P(A)−P(AB) 。
A = A B ‾ + A B A=A\overline{B} +AB A=AB+AB ,且 A B ‾ A\overline{B} AB 与 A B AB AB 互斥,由有限可加性得: P ( A B ‾ ) = P ( A ) − P ( A B ) P(A \overline{B} )=P(A)-P(AB) P(AB)=P(A)−P(AB)
4.2 加法公式
(1) P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) . P(A+B)=P(A)+P(B)-P(AB). P(A+B)=P(A)+P(B)−P(AB).
证明: A + B = ( A − B ) + ( B − A ) + A B A+B=(A-B)+(B-A)+AB A+B=(A−B)+(B−A)+AB ,且 A − B , B − A , A B A-B,B-A,AB A−B,B−A,AB 两两互斥,由有限可加性,可得: P ( A + B ) = P ( A − B ) + P ( B − A ) + P ( A B ) P(A+B)=P(A-B)+P(B-A)+P(AB) P(A+B)=P(A−B)+P(B−A)+P(AB) 再结合减法公式,有: P ( A + B ) = P ( A ) − P ( A B ) + P ( B ) − P ( B A ) + P ( A B ) = P ( A ) + P ( B ) − P ( A B ) . P(A+B)=P(A)-P(AB)+P(B)-P(BA)+P(AB)=P(A)+P(B)-P(AB). P(A+B)=P(A)−P(AB)+P(B)−P(BA)+P(AB)=P(A)+P(B)−P(AB). (2) P ( A + B + C ) = P ( A ) + P ( B ) + P ( C ) − P ( A B ) − P ( A C ) − P ( B C ) + P ( A B C ) . P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC). P(A+B+C)=P(A)+P(B)+P(C)−P(AB)−P(AC)−P(BC)+P(ABC).
4.3 条件概率公式
设 A , B A,B A,B 为两个事件,且 P ( A ) > 0 P(A)>0 P(A)>0 ,则 P ( B ∣ A ) = P ( A B ) P ( A ) . P(B | A)= \frac{P(AB)}{P(A)}. P(B∣A)=P(A)P(AB).
4.4 乘法公式
(1)设 P ( A ) > 0 P(A)>0 P(A)>0 ,则 P ( A B ) = P ( A ) P ( B ∣ A ) . P(AB)=P(A)P(B|A). P(AB)=P(A)P(B∣A).
(2) P ( A 1 A 2 … A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) … P ( A n ∣ A 1 A 2 … A n − 1 ) . P(A_1A_2 \dots A_n)=P(A_1)P(A_2|A_1)P( A_3|A_1A_2)\dots P(A_n|A_1A_2\dots A_{n-1}). P(A1A2…An)=P(A1)P(A2∣A1)P(A3∣A1A2)…P(An∣A1A2…An−1).
五、事件的独立性
5.1 事件独立的定义
5.1.1 两个事件的独立
设 A , B A,B A,B 为两个随机事件,若 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B) ,则称事件 A , B A,B A,B 相互独立。
5.1.2 三个事件的独立
设 A , B , C A,B,C A,B,C 为三个随机事件,若满足 P ( A B ) = P ( A ) P ( B ) , P ( A C ) = P ( A ) P ( C ) , P ( B C ) = P ( B ) P ( C ) , P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C), P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C), 且 P ( A B C ) = P ( A ) P ( B ) P ( C ) P(ABC)=P(A)P(B)P(C) P(ABC)=P(A)P(B)P(C) ,则称三个事件 A , B , C A,B,C A,B,C 相互独立。
5.2 事件独立的性质
性质 1 若事件 A A A 和 B B B 相互独立,则 A A A 与 B ‾ \overline{B} B 、 A ‾ \overline{A} A 与 B B B 、 A ‾ \overline{A} A 与 B ‾ \overline{B} B 也相互独立,反之亦成立。
证明:由独立可知, P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B) ,则 P ( A B ‾ ) = P ( A − B ) = P ( A ) − P ( A B ) = P ( A ) − P ( A ) P ( B ) = P ( A ) P ( B ‾ ) , P(A\overline{B})=P(A-B)=P(A)-P(AB)=P(A)-P(A)P(B)=P(A)P(\overline{B}), P(AB)=P(A−B)=P(A)−P(AB)=P(A)−P(A)P(B)=P(A)P(B), 即 A A A 与 B ‾ \overline{B} B 相互独立, A ‾ \overline{A} A 与 B B B 相互独立同理可证。
P ( A ‾ ∩ B ‾ ) = P ( A ∪ B ) ‾ = 1 − P ( A + B ) = 1 − P ( A ) − P ( B ) + P ( A B ) = [ 1 − P ( A ) ] [ 1 − P ( B ) ] = P ( A ‾ ) P ( B ‾ ) P(\overline{A}\cap \overline{B})=P(\overline{A \cup B)}=1-P(A+B)=1-P(A)-P(B)+P(AB)=[1-P(A)][1-P(B)]=P(\overline{A})P(\overline{B}) P(A∩B)=P(A∪B)=1−P(A+B)=1−P(A)−P(B)+P(AB)=[1−P(A)][1−P(B)]=P(A)P(B) ,则有 A ‾ \overline{A} A 与 B ‾ \overline{B} B 相互独立,反之证明同理。
性质 2 设 A , B A,B A,B 为两个随机事件且 P ( A ) = 0 P(A)=0 P(A)=0 或 P ( A ) = 1 P(A)=1 P(A)=1 ,则 A , B A,B A,B 相互独立。
证明:设 P ( A ) = 0 P(A)=0 P(A)=0 ,由 A B ⊂ A AB \sub A AB⊂A 可知, P ( A B ) ≤ P ( A ) = 0 P(AB) \leq P(A)=0 P(AB)≤P(A)=0 ,又因为 P ( A B ) ≥ 0 P(AB) \geq0 P(AB)≥0 ,故 P ( A B ) = 0 P(AB)=0 P(AB)=0 ,即有 P ( A B ) = P ( A ) = 0 P(AB)=P(A)=0 P(AB)=P(A)=0 ,可得 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B) ,从而有 A , B A,B A,B 相互独立。
设 P ( A ) = 1 P(A)=1 P(A)=1 , P ( A ‾ ) = 0 P(\overline{A})=0 P(A)=0 , P ( B A ‾ ) = P ( B ) − P ( A ) ≤ 1 P(B\overline{A})=P(B)-P(A) \leq1 P(BA)=P(B)−P(A)≤1 ,由 P ( A ) = 1 P(A)=1 P(A)=1 ,可知 P ( B A ‾ ) = 0 P(B\overline{A})=0 P(BA)=0 ,故 P ( B A ‾ ) = P ( A ‾ ) P ( B ) P(B\overline{A})=P(\overline{A})P(B) P(BA)=P(A)P(B) ,即有 A ‾ \overline{A} A 与 B B B 相互独立,根据性质 1 ,事件 A , B A,B A,B 相互独立。
1,事件 A , B , C A,B,C A,B,C 两两独立,则事件 A , B , C A,B,C A,B,C 不一定独立。
2,设 A , B A,B A,B 为两个随机事件,且 P ( A ) > 0 , P ( B ) > 0 P(A)>0,P(B)>0 P(A)>0,P(B)>0 ,则
若 A , B A,B A,B 独立,则 A , B A,B A,B 不互斥。因为此时 P ( A B ) = P ( A ) P ( B ) > 0 P(AB)=P(A)P(B)>0 P(AB)=P(A)P(B)>0 ,不为空集。
若 A , B A,B A,B 互斥,则 A , B A,B A,B 不独立。此时 P ( A B ) = ∅ P(AB)=\empty P(AB)=∅ ,必不可能等于 P ( A ) P ( B ) P(A)P(B) P(A)P(B) 。
设事件 A 1 , A 2 , … , A m A_1,A_2,\dots,A_m A1,A2,…,Am ,事件 B 1 , B 2 , … , B n B_1,B_2,\dots,B_n B1,B2,…,Bn 相互独立,则由事件 A 1 , A 2 , … , A m A_1,A_2,\dots,A_m A1,A2,…,Am 所构成的任意事件 φ ( A 1 , A 2 , … , A m ) \varphi(A_1,A_2,\dots,A_m) φ(A1,A2,…,Am) 与由事件 B 1 , B 2 , … , B n B_1,B_2,\dots,B_n B1,B2,…,Bn 构成的任意事件 ϕ ( B 1 , B 2 , … , B n ) \phi (B_1,B_2,\dots,B_n) ϕ(B1,B2,…,Bn) 相互独立。
写在最后
剩下一个贝叶斯和全概率,还有概型,放到后面吧。
相关文章:
)
【考研数学】概率论与数理统计 | 第一章——随机事件与概率(2,概率基本公式与事件独立)
文章目录 引言四、概率基本公式4.1 减法公式4.2 加法公式4.3 条件概率公式4.4 乘法公式 五、事件的独立性5.1 事件独立的定义5.1.1 两个事件的独立5.1.2 三个事件的独立 5.2 事件独立的性质 写在最后 引言 承接上文,继续介绍概率论与数理统计第一章的内容。 四、概…...

SpringBoot整合RabbitMQ,笔记整理
1创建生产者工程springboot-rabbitmq-produce 2.修改pom.xml文件 <!--父工程--> <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.0</version><r…...
搜狗拼音暂用了VSCode及微信小程序开发者工具快捷键Ctrl + Shit + K 搜狗拼音截图快捷键
修改搜狗拼音的快捷键 右键--更多设置--属性设置--按键--系统功能快捷键--系统功能快捷键设置--取消Ctrl Shit K的勾选--勾选截屏并设置为Ctrl Shit A 微信开发者工具设置快捷键 右键--Command Palette--删除行 微信开发者工具快捷键 删除行:Ctrl Shit K 或…...

Python包sklearn画ROC曲线和PR曲线
前言 关于ROC和PR曲线的介绍请参考: 机器学习:准确率(Precision)、召回率(Recall)、F值(F-Measure)、ROC曲线、PR曲线 参考: Python下使用sklearn绘制ROC曲线(超详细) Python绘图|Python绘制ROC曲线和PR曲线 源码 …...

snpEff变异注释的一点感想
snpEff变异注释整成人生思考 1.介绍2.安装过程以及构建物种参考数据库3.坑货来了4.结果文件判读5.小tips 1.介绍   SnpEff(Snp Effect)是一个用于预测基因组变异(例如单核苷酸变异、插入、缺失等)对基因功能的影响的生物…...

“保姆级”考研下半年备考时间表
7月-8月 确定考研目标与备考计划 暑假期间是考研复习的关键时期,需要复习的主要内容有:重点关注重要的学科和专业课程,复习相关基础知识和核心概念。制定详细的复习计划并合理安排每天的学习时间,增加真题练习熟悉考试题型和答题技…...

具有弱监督学习的精确3D人脸重建:从单幅图像到图像集的Python实现详解
随着深度学习和计算机视觉技术的飞速发展,3D人脸重建技术在多个领域获得了广泛应用,例如虚拟现实、电影特效、生物识别等。但是,由单幅图像实现高精度的3D人脸重建仍然是一个巨大的挑战。在本文中,我们将探讨如何利用弱监督学习进…...

查询投稿会议的好用网址
会议伴侣 https://www.myhuiban.com/ 艾思科蓝 https://www.ais.cn/...

一元三次方程的解
一元三次方程的解法,点击跳转知乎原文地址 (一)一元三次方程降阶 一元三次方程原型: a x 3 b x 2 c x d 0 a x^3 b x^2 cx d 0 ax3bx2cxd0 代换削元。最简单的方法是线性变化削元。假设x my n, 带入后可以削去未知数…...
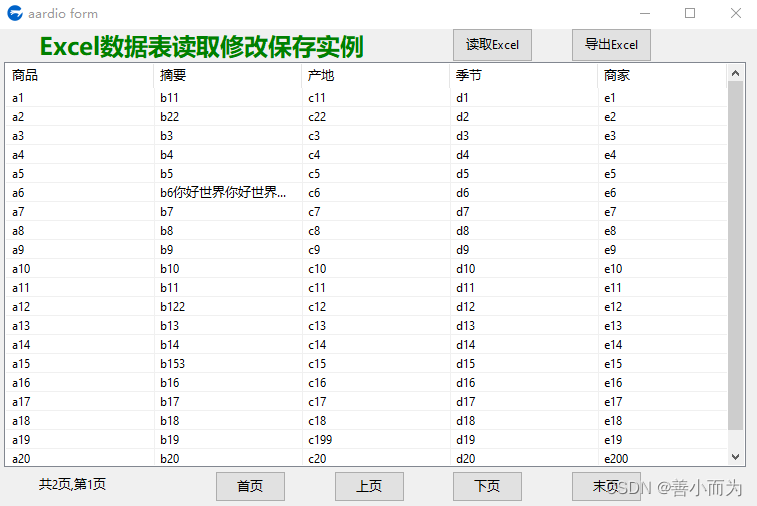
aardio开发语言Excel数据表读取修改保存实例练习
import win.ui; /*DSG{{*/ var winform win.form(text"aardio form";right759;bottom479) winform.add( buttonEnd{cls"button";text"末页";left572;top442;right643;bottom473;z6}; buttonExcelRead{cls"button";text"读取Exce…...
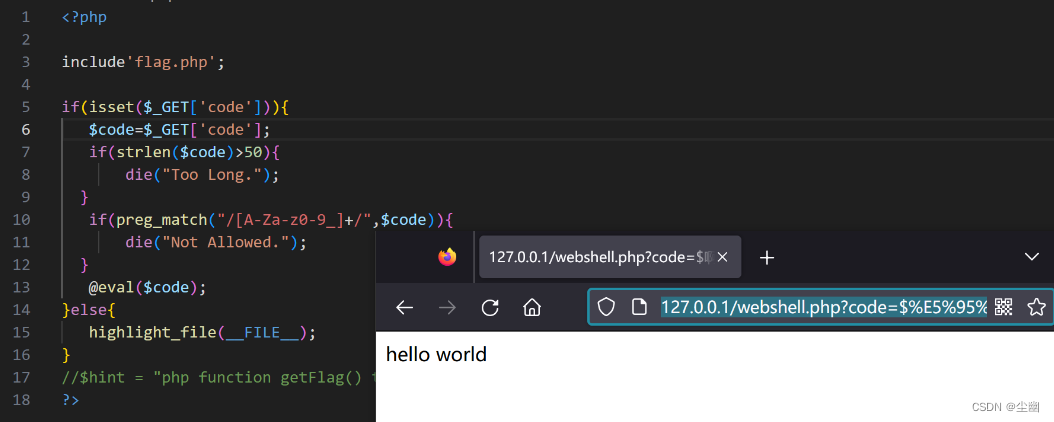
webshell绕过
文章目录 webshell前置知识进阶绕过 webshell 前置知识 <?phpecho "A"^""; ?>运行结果 可以看到出来的结果是字符“!”。 为什么会得到这个结果?是因为代码的“A”字符与“”字符产生了异或。 php中,两个变…...
Spring Boot 统一功能处理
目录 1.用户登录权限效验 1.1 Spring AOP 用户统一登录验证的问题 1.2 Spring 拦截器 1.2.1 自定义拦截器 1.2.2 将自定义拦截器加入到系统配置 1.3 拦截器实现原理 1.3.1 实现原理源码分析 2. 统一异常处理 2.1 创建一个异常处理类 2.2 创建异常检测的类和处理业务方法 3. 统一…...
图像处理常见的两种拉流方式
传统算法或者深度学习在进行图像处理之前,总是会首先进行图像的采集,也就是所谓的拉流。解决拉流的方式有两种,一个是直接使用opencv进行取流,另一个是使用ffmpeg进行取流,如下分别介绍这两种方式进行拉流处理。 1、o…...

数据可视化数据调用浅析
数据可视化是现代数据分析和决策支持中不可或缺的一环。它将数据转化为图形、图表和可视化工具,以便更直观地理解和解释数据。在数据可视化的过程中,数据的调用和准备是关键的一步。本文将探讨数据可视化中的数据调用过程,并介绍一些常用的数…...
恒运资本:CPO概念发力走高,兆龙互联涨超10%,华是科技再创新高
CPO概念15日盘中发力走高,截至发稿,华是科技涨超15%再创新高,兆龙互联涨逾11%,中贝通讯涨停,永鼎股份、太辰光涨超5%,天孚通讯涨逾4%。 消息面上,光通讯闻名咨询机构LightCounting近日发布的202…...
【蓝桥杯】[递归]母牛的故事
原题链接:https://www.dotcpp.com/oj/problem1004.html 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 我们列一个年份和母牛数量的表格: 通过观察,找规律,我们发现: 当年份小于等于4时&…...
使用RDP可视化远程桌面连接Linux系统
使用RDP可视化远程桌面连接Linux系统 远程桌面连接Linux安装安装包准备服务器安装xrdp远程连接 远程桌面连接Linux 通常使用SSH来连接服务器,进行命令行操作,但是这次需要远程调试生产环境的内网服务器,进行浏览器访问内网网站,至…...
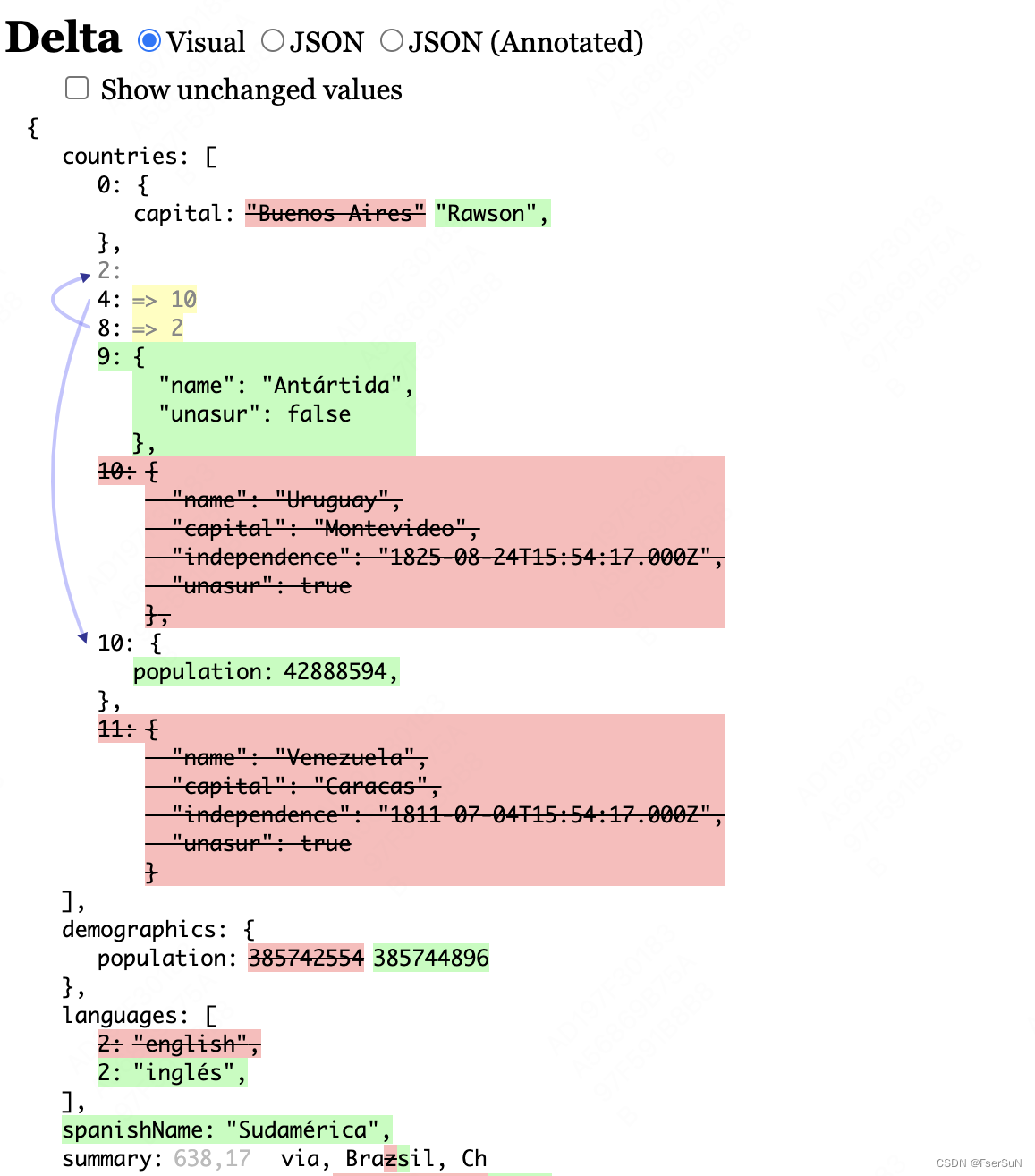
数据可视化diff工具jsondiffpatch使用学习
1.jsondiffpatch 简介 jsondiffpatch 是一个用于比较和生成 JSON 数据差异的 JavaScript 库。它可以将两个 JSON 对象进行比较,并生成一个描述它们之间差异的 JSON 对象。这个差异对象可以用于多种用途,例如: 生成可视化的差异报告应用差异…...
pdf 转 word
pdf 转 word 一、思路 直接调用LibreOffice 命令进行文档转换的命令行工具 使用的前系统中必须已经安装了 libreofficelibreoffice已翻译的用户界面语言包: 中文 (简体)libreoffice离线帮助文档: 中文 (简体)上传字体 重点:重点:重点: 亲…...
【数据结构OJ题】设计循环队列
原题链接:https://leetcode.cn/problems/design-circular-queue/ 1. 题目描述 2. 循环队列的概念和结构 为充分利用向量空间,克服"假溢出"现象的方法是:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
