力扣题解(1030. 距离顺序排列矩阵单元格),带注释
题目描述
链接:点我
注意:多看几遍题目,开始没看懂…相当于计算矩阵网格里面的点(不要计算边界) 我开了题解才明白题的意思 orz…
题解
class Solution {public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {int ans[][] = new int[rows*cols][]; // 是一个二维整数数组,用于存储排序后的单元格坐标。for(int i = 0;i<rows;i++){for(int j=0;j<cols;j++)//将矩阵中的每个单元格的行索引 i 和列索引 j 存储在 ans 数组的相应位置上,从而形成一个具有二维坐标信息的数组。ans[cols*i + j] = new int[]{i,j}; //}// 自定义数组排序 参考:https://blog.csdn.net/qq_45733304/article/details/124350468Arrays.sort(ans, new Comparator<int[]>() {@Overridepublic int compare(int[] o1, int[] o2) {//升序排列 下标0表示行,1表示列return (Math.abs(o1[0] - rCenter) + Math.abs(o1[1] - cCenter))-(Math.abs(o2[0] - rCenter) + Math.abs(o2[1] - cCenter)); }});return ans;}
}
相关文章:
,带注释)
力扣题解(1030. 距离顺序排列矩阵单元格),带注释
题目描述 链接:点我 注意:多看几遍题目,开始没看懂…相当于计算矩阵网格里面的点(不要计算边界) 我开了题解才明白题的意思 orz… 题解 class Solution {public int[][] allCellsDistOrder(int rows, int cols, int rCenter, …...
每天一道leetcode:剑指 Offer 34. 二叉树中和为某一值的路径(中等图论深度优先遍历递归)
今日份题目: 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例1 输入:root [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSu…...
利用POM完成脚本分离实现企业级自动化(POM设计模式+页面的框架封装+测试报告截图)
利用POM完成脚本分离实现企业级自动化(POM设计模式页面的框架封装测试报告截图) 项目-测试-手工测试 项目-测试-手工测试 1.了解需求; 2.编写测试用例(开始)——功能测试组会去做的事情 3.执行测试用例——发送测试报…...
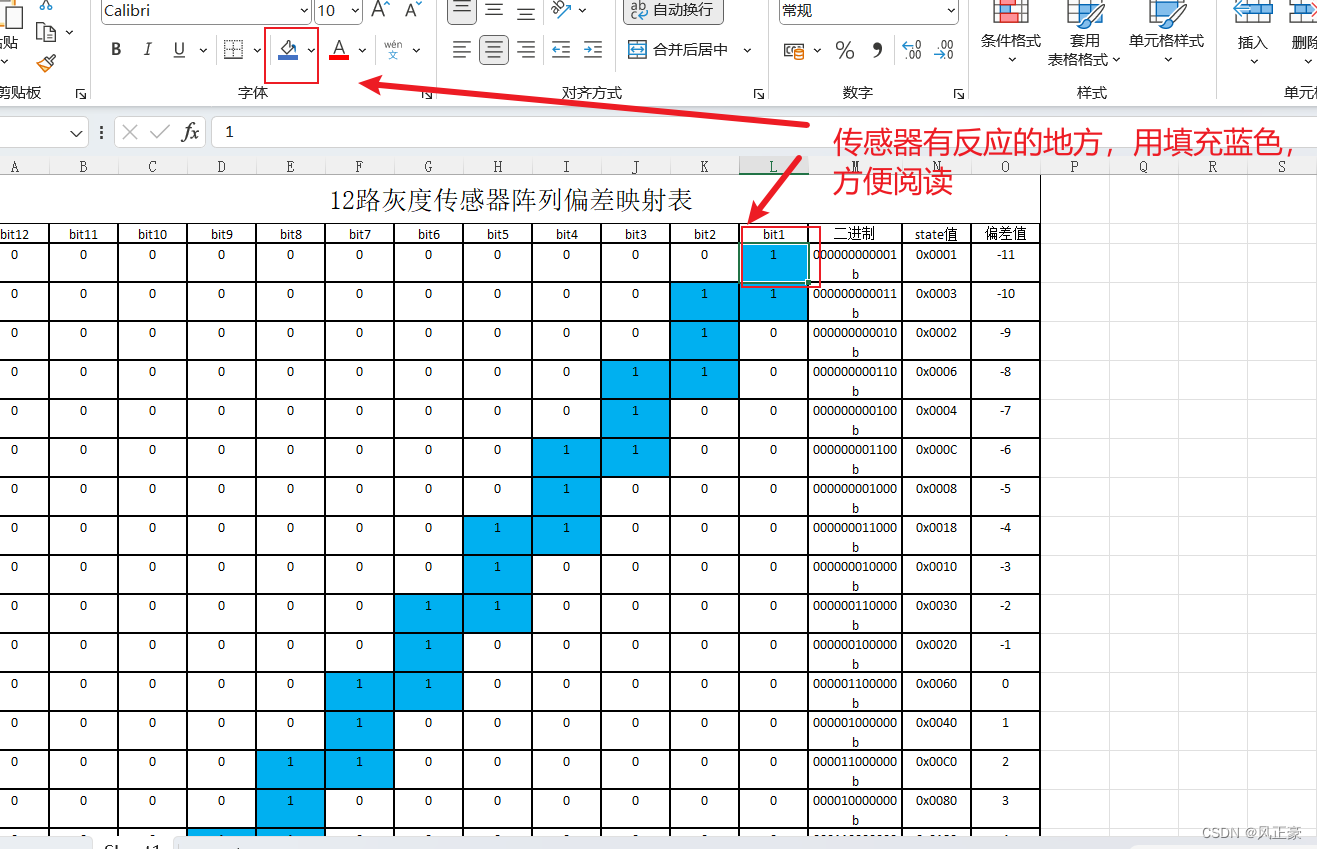
嵌入式设计中对于只有两种状态的变量存储设计,如何高效的对循迹小车进行偏差量化
前言 (1)在嵌入式程序设计中,我们常常会要对各类传感器进行数据存储。大多时候的传感器,例如红外光传感器,返回的数据要么是0,要么是1。因此,只需要一bit就能够存储。而很多人却常常使用char型数…...

day53 第九章 动态规划part14● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划
1143. 最长公共子序列 class Solution {public int longestCommonSubsequence(String text1, String text2) {int m text1.length();int n text2.length();int[][] dp new int[m 1][n 1];for (int i 1; i < m; i) {for (int j 1; j < n; j) {if (text1.charAt(i …...

shell编程 基础
将content.txt文件中的内容输出到控制台上 将content.txt中有tom的行输出到控制台 将$2文件中含有gree的行输出到控制台 case语法 简易计算器 查找有root的行 查找以root开头的行 查询时忽略大小写 grep -E 则适用于复杂的正则表达式,可以使用多项选择、重复和子表达…...

人工智能在网络安全中的应用: 分析人工智能、机器学习和深度学习等技术在预测、检测和应对网络攻击中的作用
第一章:引言 随着信息技术的迅猛发展,网络安全已成为当今社会不容忽视的重要议题。网络攻击手法日益复杂,传统的防御方法已经不再足够。在这一背景下,人工智能(AI)技术正逐渐崭露头角,为网络安…...

使用 Redis 实现异步队列
使用 Redis 实现异步队列 一、简介1 异步队列2 异步队列与同步队列 二、Redis 实现异步队列1 利用 Redis 的 List 数据类型实现异步队列2 利用 Redis 的 Pub/Sub 功能实现异步队列3 利用 Redis 的 Sorted Set 数据类型实现延迟队列 三、Redis 异步队列的实际应用场景4.1 异步任…...
RocketMQ、Dashboard部署以及安全设置
RocketMQ、dashboard部署以及安全设置 一、启动RocketMQ1.1 下载RocketMQ1.2 修改配置文件1.2.1 修改nameServer Jvm内存配置1.2.2 修改broker参数 1.3 启动1.3.1 启动NameServer1.3.2 启动Broker1.3.3 测试是否启动成功1.3.3.1 测试消息发送1.3.3.2 测试消息接收1.3.3.3 Java程…...

Android AlarmManager设置闹钟
官网镇楼:设置重复闹铃时间 闹钟具有以下特征: 它们可让您按设定的时间和/或间隔触发 intent。您可以将它们与广播接收器结合使用,以启动服务以及执行其他操作。它们在应用外部运行,因此即使应用未运行,或设备本身处…...

【C# 基础精讲】LINQ to XML查询
LINQ to XML 是 C# 中用于查询和操作 XML 数据的强大工具。它允许您使用 LINQ 查询语法对 XML 文档进行查询、过滤、投影等操作,从而更加方便地处理 XML 数据。本文将详细介绍 LINQ to XML 的基本概念、常见操作以及示例,帮助您了解如何在 C# 中使用 LIN…...
标识符命名规则和规范)
Java学习笔记——(20)标识符命名规则和规范
什么叫标识符 Java 对各种变量、方法和类等命名时使用的字符序列成为标识符凡是自己可以起名字的地方都叫标识符 标识符的命名规则(必须遵守) 由26个英文字母大小写,0-9,_ 或 $ 组成数字不可以开头不可以使用关键字和保留字Jav…...

过滤字符,绕过
构造不包含字母和数字的webshell <?phpecho "A"^""; ?>运行结果为! 代码中对字符"A"和字符”"进行了异或操作。在PHP中,两个变量进行异或时,先会将字符串转换成ASCII值,再将ASCII值转换成二进制…...

Apache Doris 入门教程32:物化视图
物化视图 物化视图是将预先计算(根据定义好的 SELECT 语句)好的数据集,存储在 Doris 中的一个特殊的表。 物化视图的出现主要是为了满足用户,既能对原始明细数据的任意维度分析,也能快速的对固定维度进行分析查询。 …...
函数详解,PHP截取字符串。)
PHP substr()函数详解,PHP截取字符串。
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:对网络安全感兴趣的小伙伴可以关注专栏《网络安全入门到精通》 substr 一、截取字符串二、截取中文字符串三、leng…...

关于flink-sql-connector-phoenix的重写逻辑
目录 重写意义 代码结构 调用链路 POM文件配置 代码解析 一、PhoenixJdbcDynamicTableFactory...
Django进阶:DRF(Django REST framework)
什么是DRF? DRF即Django REST framework的缩写,官网上说:Django REST framework是一个强大而灵活的工具包,用于构建Web API。 简单来说:通过DRF创建API后,就可以通过HTTP请求来获取、创建、更新或删除数据(…...

Flink CDC系列之:Oracle CDC 导入 Elasticsearch
Flink CDC系列之:Oracle CDC 导入 Elasticsearch 一、深入理解Flink Oracle CDC Connector二、创建docker-compose.yml文件三、启动容器四、下载Flink Oracle CDC的jar包五、启动 Flink 集群,再启动 SQL CLI六、检查 ElasticSearch 中的结果七、在 Oracl…...
Linux忘记root密码解决方法
当我们忘记root密码进不去服务器怎么办?不要担心,可以进入到linux的救援模式修改root密码。 下面直接上干货,流程如下: 1.重启电脑,按上下键滑动,保证不进入开机流程,然后按e键 2.出现此页面…...

AR/VR眼镜转接器方案,实现同时传输视频快充方案
简介 虚拟现实头戴显示器设备,简称VR头显VR眼镜,是利用仿真技术与计算机图形学人机接口技术多媒体技术传感技术网络技术等多种技术集合的产品,是借助计算机及最新传感器技术创造的一种崭新的人机交互手段。VR头显VR眼镜是一个跨时代的产品。不…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
