函数(2)
6. 函数的声明和定义
6.1 函数声明:
1. 告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,函数
声明决定不了。
2. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。
3. 函数的声明一般要放在头文件中的。
函数的声明
int Add(int x, int y);int main()
{int num1 = 0;int num2 = 0;scanf("%d %d", &num1, &num2);//计算//函数的调用(传值调用)//2int ret = Add(num1, num2);printf("%d\n", ret);return 0;
}//函数的定义
int Add(int x, int y)
{return x + y;
}6.2 函数定义
函数的定义是指函数的具体实现,交待函数的功能实现。
函数的定义本就是一种特殊的声明。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//函数的定义
int Add(int x, int y)
{return x + y;
}int main()
{int num1 = 0;int num2 = 0;scanf("%d %d", &num1, &num2);//计算//函数的调用(传值调用)//2int ret = Add(num1, num2);printf("%d\n", ret);return 0;
}以后我们可以把函数的声明放在同一头文件中,这样方便管理。
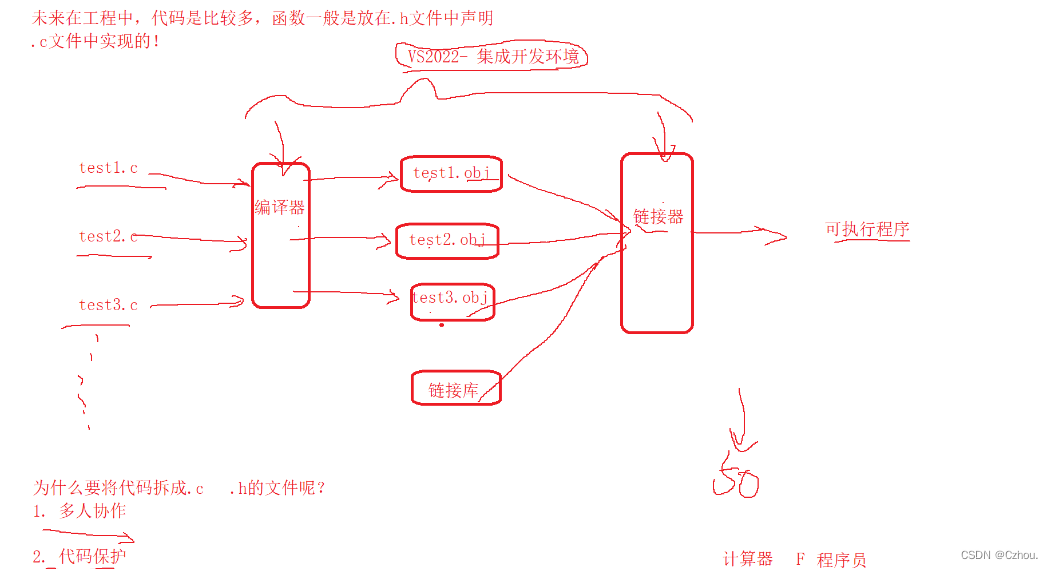
7. 函数递归
7.1 什么是递归?
程序调用自身的编程技巧称为递归( recursion)。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接
调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
递归的主要思考方式在于:把大事化小。
7.2 递归的两个必要条件
存在限制条件,当满足这个限制条件的时候,递归便不再继续。
每次递归调用之后越来越接近这个限制条件。
7.2.1 练习1:
接受一个整型值(无符号),按照顺序打印它的每一位。
例如:
输入:1234,输出 1 2 3 4
不用递归的方法得到的是这样的
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int main()
{int num = 0;scanf("%d", &num);while (num){printf("%d ", num%10);num = num / 10;}return 0;
}
我们用递归来实现:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void Print(int n)
{if (n > 9){Print(n/10);}printf("%d ", n % 10);
}
int main()
{int num = 0;scanf("%d", &num);//1234Print(num);return 0;
}
其实递归分为两步,递推和回归,我们把递推实现到最后一步再进行回归。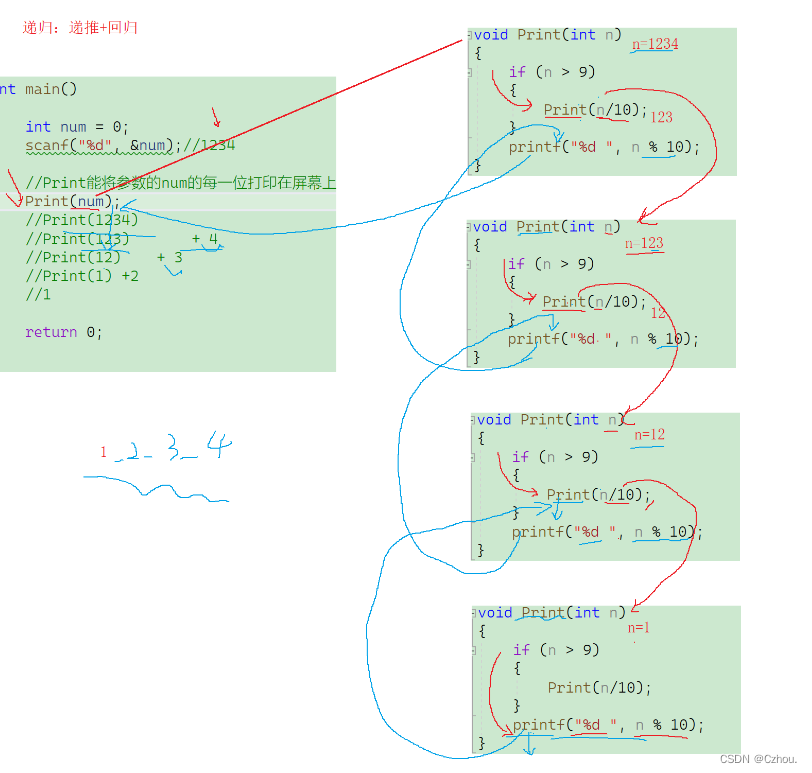
7.2.2 练习2:
编写函数不允许创建临时变量,求字符串的长度。
大家都知道求字符串长度用strlen就可以了,但是我们用递归的方式也能够实现。
实现我们来看一下strlen实现,strlen函数是统计/0之前的字符串长度,遇到/0就会停止。
strlen这个函数的返回类型是size_t,size_t 类型的数据打印的时候使用%zd,size_t 是一种类型,是无符号整型的,size_t就是为sizeof设计的。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
int main()
{char arr[] = "abc";size_t len = strlen(arr);printf("%zd\n", len);return 0;
}我们用递归来实现一下:
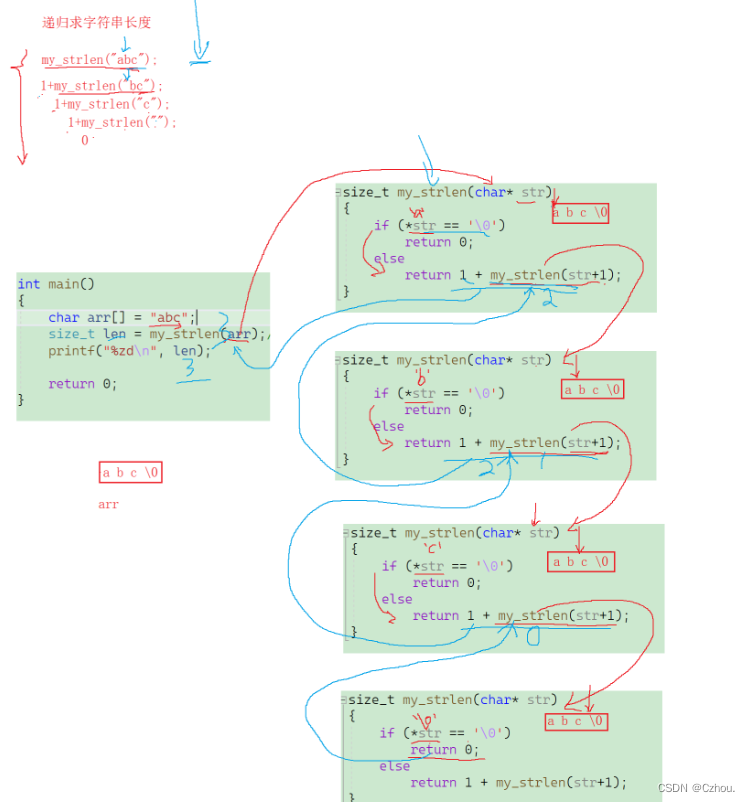
用递归来实现的话就相当于模拟实现strlen。数组传参的话传过去的是首元素的地址,传过去的是a的地址,所以我们用char*来接收,我们用if来判断首元素是不是/0,如果不是则+1并且(str+1)统计下一位元素,如此循环往复就可以进行递归了,直到遇到/0停下来。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
size_t my_strlen(char* str)
{if (*str == '\0')return 0;elsereturn 1 + my_strlen(str + 1);
}
int main()
{char arr[] = "abc";size_t len = my_strlen(arr);//传递的是数组首元素的地址printf("%zd\n", len);return 0;
}
7.3 递归与迭代
7.3.1 练习3:
求n的阶乘。(不考虑溢出)
在数学里面阶乘就是这样定义的,我们可以发现用递归来实现就很容易了。

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int Fac(int n)
{if (n <= 1)return 1;elsereturn n* Fac(n - 1);
}
int main()
{int n = 0;scanf("%d", &n);int r = Fac(n);printf("%d\n", r);return 0;
}7.3.2 练习4:
求第n个斐波那契数。(不考虑溢出)
斐波那契·数就是前面二个数等于第三个数。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int Fib(int n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret);return 0;
}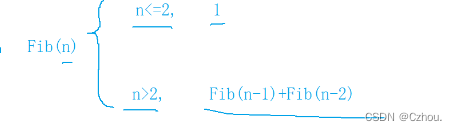
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n >= 3){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret);return 0;
}但是我们发现有问题;
在使用 fib 这个函数的时候如果我们要计算第50个斐波那契数字的时候特别耗费时间。
使用 factorial 函数求10000的阶乘(不考虑结果的正确性),程序会崩溃。
为什么呢?
我们发现 fib 函数在调用的过程中很多计算其实在一直重复。
提示:
1. 许多问题是以递归的形式进行解释的,这只是因为它比非递归的形式更为清晰。
2. 但是这些问题的迭代实现往往比递归实现效率更高,虽然代码的可读性稍微差些。
3. 当一个问题相当复杂,难以用迭代实现时,此时递归实现的简洁性便可以补偿它所带来的运行时开销。
这篇文章到这里就结束啦!感谢烙铁们的阅读,下篇我们将详细的讲解数组,让我们下期再见。
相关文章:

函数(2)
6. 函数的声明和定义 6.1 函数声明: 1. 告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,函数 声明决定不了。 2. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。 3. 函数的声明一般要放…...

Linux笔试题(4)
67、在局域网络内的某台主机用ping命令测试网络连接时发现网络内部的主机都可以连同,而不能与公网连通,问题可能是__C_ A.主机ip设置有误 B.没有设置连接局域网的网关 C.局域网的网关或主机的网关设置有误 D.局域网DNS服务器设置有误 解析:在局域网络内的某台主…...

Selenium的使用:WEB功能测试
Selenium是ThrougthWorks公司一个强大的开源WEB功能测试工具系列,本系统包括多款软件 Selenium语言简单,用(Command,target,value)三种元素组成一个行为,并且有协助录制脚本工具,但Selenese有一些严格的限制: …...
从入门到精通系列之十七:minikube启动K8s dashboard)
Kubernetes(K8s)从入门到精通系列之十七:minikube启动K8s dashboard
Kubernetes K8s从入门到精通系列之十七:minikube启动K8s dashboard 一、安装minikube的详细步骤二、查看Pod三、启动dashboard四、创建代理访问dashboard五、远程访问dashboard一、安装minikube的详细步骤 Kubernetes(K8s)从入门到精通系列之十六:linux服务器安装minikube的详…...

C++ 网络编程项目fastDFS分布式文件系统(五)--nginx+fastdfs
目录 1. 文件上传下载流程 2. Nginx和fastDFS的整合 3. 数据库表 3.1 数据库操 3.2 数据库建表 1. 文件上传下载流程 fileID 需要是一个哈希来判定。 2. 文件下载流程 3. 优化 优化思路 : 直接让客户端连接 fastDFS 的存储节点 , 实现文件下载 举例 , 访问一个…...
)
开发者本地搭建性能监测工具(Windows)
ElasticSearch 8.9.0 开发模式安装 JDK安装 官方提供版本与JDK支持关系:https://www.elastic.co/cn/support/matrix#matrix_jvm 我们安装Elasticsearch 8.9.x,看到支持的最低JDK版本是17。 JDK(Windows/Mac含M1/M2 Arm原生JDK)…...

嵌入式Linux开发实操(八):UART串口开发
串口可以说是非常好用的一个接口,它同USB、CAN、I2C、SPI等接口一样,为SOC/MCU构建了丰富的接口功能。那么在嵌入式linux中又是如何搭建和使用UART接口的呢? 一、Console接口即ttyS0 ttyS0通常做为u-boot(bootloader的一种,像是Windows的BIOS),它需要一个交互界面,一般…...

公告:微信小程序备案期限官方要求
备案期限要求 1、若微信小程序未上架,自2023年9月1日起,微信小程序须完成备案后才可上架,备案时间1-20日不等; 2、若微信小程序已上架,请于2024年3月31日前完成备案,逾期未完成备案,平台将按照…...

cesium中获取高度的误区
this.ellipsoid viewer.scene.globe.ellipsoid; var cartesian viewer.camera.pickEllipsoid(e.position, this.ellipsoid);if(cartesian){// 苗卡尔椭球体的三维坐标 转 地图坐标(弧度)var cartographic viewer.scene.globe.ellipsoid.cartesianToCa…...

基于Centos:服务器基础环境安装: JDK、Maven、Python、Go、Docker、K8s
创建用户 useradd dev groupadd op chown -R :op /opt chmod -R 770 /opt usermod -aG op devJDK8 yum install -y java-1.8.0-openjdk-devel echo export JAVA_HOME/usr/lib/jvm/java-1.8.0/>> /etc/profilesource /etc/profileJDK11 yum install -y java-11-openjd…...

Elasticsearch的数据删除策略只能触发一次
在Elasticsearch中,可以使用Index Lifecycle Management(ILM)来设置删除数据的保留时长。ILM是Elasticsearch的一项功能,用于管理索引的生命周期,包括数据保留、备份、归档等操作。 要设置删除数据的保留时长…...

Open3D 最小二乘拟合空间直线(方法一)
目录 一、算法原理1、空间直线2、最小二乘法拟合二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、空间直线 x −...

解决uniapp 二次登陆 登录页是首页时,登录页闪现问题
pages.json文件中,pages数组中第一项是登录页,用户第一次登录后,存储登录状态,以后再进入应用时,自动登录跳转至首页。 但是自动登录跳转至首页时,登录页总是会闪现一下。 第一步:manifest.js…...
如何快速制作一个房地产电子传单?
在如今高度数字化的时代,电子传单成为了宣传推广的一种重要方式。下面将介绍如何利用乔拓云平台快速制作一个房地产电子传单。 第一步,找一个可靠的第三方制作平台/工具,比如乔拓云平台。乔拓云平台是一个功能强大、简单易用的电子传单制作工…...
golang云原生项目之:etcd服务注册与发现
服务注册与发现:ETCD 1直接调包 kitex-contrib: 上面有实现的案例,直接cv。下面是具体的理解 2 相关概念 EtcdResolver: etcd resolver是一种DNS解析器,用于将域名转换为etcd集群中的具体地址,以便应用程序可以与et…...
arm:day4
1. 实现三盏灯的点亮 .text .global _start_start: led1初始化函数LED_INIT: 1 通过RCC_AHB4_ENSETR寄存器,设置GPIOE F组控制器使能 0x50000A28[5:4]1ldr r0,0X50000A28ldr r1,[r0]orr r1,r1,#(0X3<<4)str r1,[r0] 2.1 通过GPIOE_MODER寄存器,…...
flutter 常见的状态管理器
flutter 常见的状态管理器 前言一、Provider二、Bloc三、Redux四、GetX总结 前言 当我们构建复杂的移动应用时,有效的状态管理是至关重要的,因为应用的不同部分可能需要共享数据、相应用户交互并保持一致的状态。Flutter 中有多种状态管理解决方案&#…...

Kotlin的Map
在 Kotlin 中,Map 是一种键值对的集合数据结构,用于存储一组关联的键和值。Kotlin 标准库提供了 Map 接口和多种实现类,使得操作和处理键值对数据更加方便。下面详细描述 Kotlin 的 Map 的用法: 创建 Map Kotlin 提供了几种方式…...
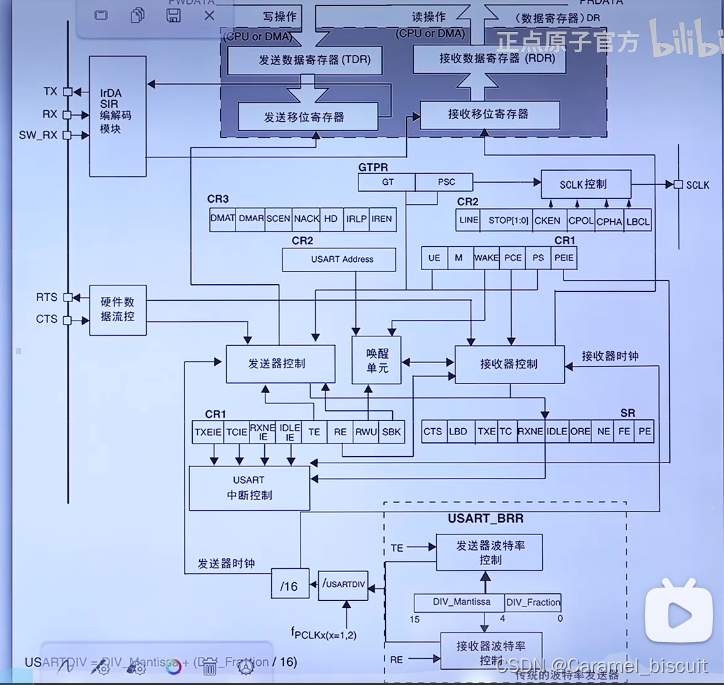
STM32 串口复习
按数据通信方式分类: 串行通信:数据逐位按顺序依次传输。传输速率较低,抗干扰能力较强,通信距离较长,I/O资源占用较少,成本较低。并行通信:数据各位通过多条线同时传输。 按数据传输方向分类&…...
VScode替换cmd powershell为git bash 终端,并设置为默认
效果图 步骤 1. 解决VScode缺少git bash的问题_failed to start bash - is git-bash.exe on the syst_Rudon滨海渔村的博客-CSDN博客效果解决步骤找到git安装目录下的/bin/bash.exe,复制其绝对路径,例如D:\Program Files\Git\bin\bash.exe把路径的右斜…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
