2023牛客暑期多校训练营9 B.Semi-Puzzle: Brain Storm
文章目录
- 题目大意
- 题解
- 求解
- 回溯
- 参考代码
题目大意
给定两个数 a , m a,m a,m ,求满足 a u ≡ u ( m o d m ) a^u \equiv u (mod\ \ m) au≡u(mod m) 的一个解。
( 1 ≤ a , m ≤ 1 0 9 , 0 ≤ u ≤ 1 0 18 ) (1\leq a,m \leq10^9 ,0\leq u\leq 10^{18}) (1≤a,m≤109,0≤u≤1018)
题解
参考了讨论区 https://blog.nowcoder.net/n/576f9463036346f0a0fb04fee50fac75 的方法
求解
考虑使用欧拉定理,考虑 b > = ϕ p b>=\phi_p b>=ϕp的情况。
a u ≡ { a u % ϕ m g c d ( a , u ) = 1 a u % ϕ i + ϕ m g c d ( a , u ) ! = 1 ( m o d m ) a^u\equiv\begin{cases}a^{u\% \phi_m }&gcd(a,u)=1\\a^{u\% \phi_i+\phi_m}& gcd(a,u)!=1\end{cases}(mod \ m) au≡{au%ϕmau%ϕi+ϕmgcd(a,u)=1gcd(a,u)!=1(mod m)
定义 d = u % ϕ m d=u\%\phi_m d=u%ϕm 或 u % ϕ m + ϕ m u\%\phi_m+\phi_m u%ϕm+ϕm 和
k ∗ ϕ p + d = u ( k > = 0 ) k*\phi_p+d=u(k>=0) k∗ϕp+d=u(k>=0)
则原式可以转化为 a d ≡ d + k ∗ ϕ m ( m o d m ) a^d \equiv d+k*\phi_m (mod\ m) ad≡d+k∗ϕm(mod m)
移项可以得到 a d − d ≡ k ∗ ϕ m ( m o d m ) a^d-d\equiv k*\phi_m(mod\ m) ad−d≡k∗ϕm(mod m)
ϕ m ∗ x 1 + m ∗ y 1 ≡ g c d ( ϕ m , m ) ( m o d m ) \phi_m*x1+m*y1\equiv gcd(\phi_m,m) (mod \ m) ϕm∗x1+m∗y1≡gcd(ϕm,m)(mod m) 是一个已知有解的同余方程
回到上一个方程想要得到解 k k k ,显然要满足 a d − d = x ∗ g c d ( m , ϕ m ) , ( x > 0 ) a^d-d=x *gcd(m,\phi_m),(x>0) ad−d=x∗gcd(m,ϕm),(x>0)
也就是 a d ≡ d ( m o d g c d ( m , ϕ m ) ) a^d \equiv d (mod \ gcd(m,\phi_m)) ad≡d(mod gcd(m,ϕm))。
重新得到了题目,但是模数缩小了,因此我们想到了递归,直到模数为 1 1 1 时直接推出答案。
回溯
假设我们已经得到了最后一组解 d = 0 d=0 d=0 ,
求解同余方程 a d − d ≡ k ∗ ϕ m ( m o d m ) a^d-d\equiv k*\phi_m(mod\ m) ad−d≡k∗ϕm(mod m),使用扩展欧几里得定理,推出 x 1 x1 x1 的值,
k = x 1 ∗ a d − d g c d ( m , ϕ m ) % m o d k=x1*\frac{a^d-d}{gcd(m,\phi_m)}\%mod k=x1∗gcd(m,ϕm)ad−d%mod
由于 a d a^d ad 超出范围,根据 a b % ( b ∗ c ) = a % ( b ∗ c ) b \frac{a}{b}\%(b*c)=\frac{a\%(b*c)}{b} ba%(b∗c)=ba%(b∗c)得出
k = x 1 ∗ ( a d − d ) % m / ϕ m k=x1*(a^d-d)\%m/\phi_m k=x1∗(ad−d)%m/ϕm 。
再利用 k ∗ ϕ p + d = u k*\phi_p+d=u k∗ϕp+d=u,得出结果即可。
参考代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll phi(ll x)
{ll ans=x;for(int i=2;i*i<=x;i++){if(x%i==0)ans=ans/i*(i-1);while(x%i==0)x/=i;}if(x!=1)ans=ans/x*(x-1);return ans;
}
ll ksm(ll a,ll b,ll p)
{ll res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{if(!b){x=1,y=0;return a;}ll k=exgcd(b,a%b,y,x);y-=a/b*x;return k;
}
int n,T;
ll a,m;
ll work(ll a,ll p) //递归求解
{if(p==1)return 0;ll m=phi(p);ll b=work(a,__gcd(m,p))+m;ll x,y;ll d=exgcd(m,p,x,y);ll k=(((x*(ksm(a,b,p)-b+p))%p+p)%p/d); //回溯求值return k*m+b;
}
int main()
{cin>>T;while(T--){scanf("%lld%lld",&a,&m);printf("%lld\n",work(a,m));}
}
相关文章:

2023牛客暑期多校训练营9 B.Semi-Puzzle: Brain Storm
文章目录 题目大意题解求解回溯 参考代码 题目大意 给定两个数 a , m a,m a,m ,求满足 a u ≡ u ( m o d m ) a^u \equiv u (mod\ \ m) au≡u(mod m) 的一个解。 ( 1 ≤ a , m ≤ 1 0 9 , 0 ≤ u ≤ 1 0 18 ) (1\leq a,m \leq10^9 ,0\leq u\leq 10^{18}) (1≤a…...
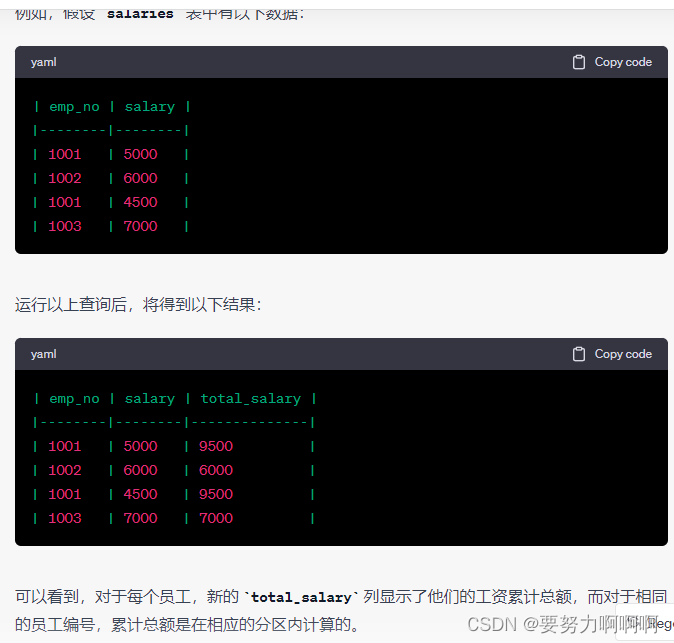
mysql中的窗口函数
MySQL中的窗口函数(Window Functions)是一种用于在查询结果集内执行计算的功能。窗口函数可以在查询中进行分析和聚合操作,而无需将查询结果分组。它们可以用于计算排名、行号、累积值等各种分析操作。窗口函数通常与OVER子句一起使用&#x…...

【双指针】经典数组双指针题LeetCode
文章目录 27. 移除元素 简单283. 移动零 简单🔥167. 两数之和 II - 输入有序数组 中等11. 盛最多水的容器 中等🔥15. 三数之和 中等(N数之和)中等🔥42. 接雨水 困难 🔥26. 删除有序数组中的重复项 简单5. 最…...

极智嘉x吉利汽车 x京东物流,引领汽车行业智慧物流新变革!
近日,中国领先的汽车制造商吉利汽车携手中国领先的技术驱动的供应链解决方案及物流服务商京东物流、全球仓储机器人引领者极智嘉(Geek),在西安吉利汽车制造基地RDC仓库率先落地SkyPick上存下拣解决方案,实现了全物流链精益化、智能化、一体化…...

RK3588平台开发系列讲解(AI 篇)RKNN C API 详细说明
文章目录 一、API 硬件平台支持说明二、API 函数介绍2.1、rknn_init2.2、rknn_destroy2.3、rknn_query2.4、rknn_inputs_set2.5、rknn_run2.6、rknn_outputs_get2.7、rknn_outputs_release沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇章主要讲解 RKNN C API 详细…...

【基础】Android Handler
一、博客参考 Handler机制详解【重点】:https://www.jianshu.com/p/b4d745c7ff7a Handler Thread工作线程操作UI范例【重点】:https://www.cnblogs.com/net168/p/4075126.html 二、内存泄漏的解决:静态内部类弱引用 关于 Handler…...
c语言实现MD5算法
MD5加密 文章目录 MD5加密MD5介绍应用场景代码分析 (基于qt5.14.2)测试记录 MD5介绍 1。 一种单向加密算法,即对明文加密,而不能通过密文得到明文。对原数据的任何改动,哪怕是1字节,得到的MD5值都有很大的区…...

Apache Doris 2.0.0 特性分析
1、存算分离 所谓存算分离是指查询外表时,使用一种专门做计算的BE节点,但对于存储在BE上的内部表,目前还不能做到存储分离。 doris可以查询外部表,包括: Hive、Iceberg、Hudi、Elasticsearch、JDBC、Paimon 早期版本中…...

如何做H5性能测试?
提起H5性能测试,可能许多同学有所耳闻,但是不知道该如何对H5做性能测试,或者不知道H5应该关注哪些性能指标。今天我们就来看下,希望阅读本文后,能够有所了解。 常用指标 1、H5性能相关参数介绍 白屏时间:…...
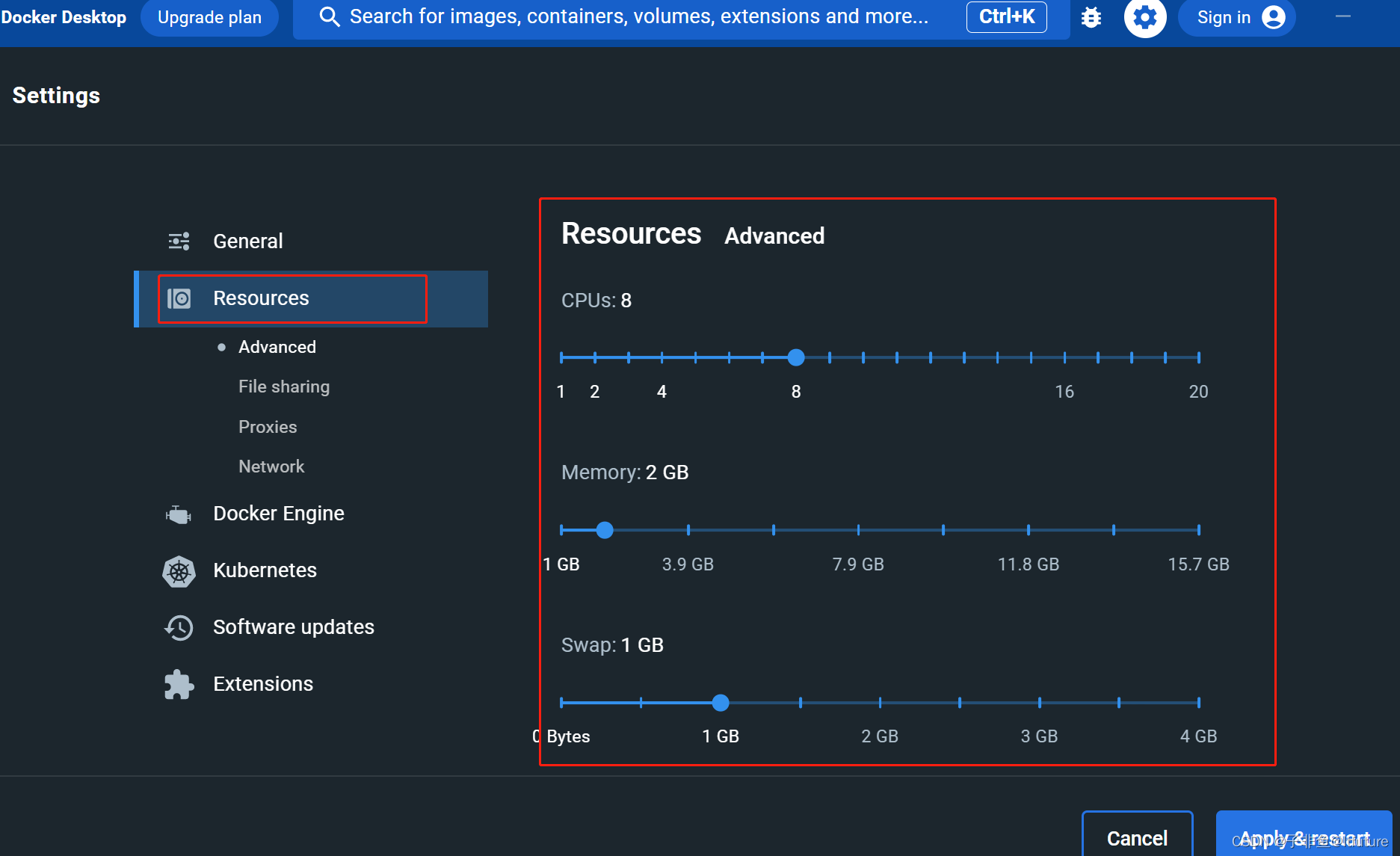
【Docker】Docker Desktop配置资源:cpu、内存等(windows环境下)
Docker Desktop配置资源:cpu、内存等(windows环境下) 一、WSL2 以及 hyper-v区别,二者安装docker desktop1.WSL2和hyper-v区别2.安装Docker Desktop 二、docker desktop限额配置,资源配置方法 Docker 是指容器化技术&a…...

8.2.tensorRT高级(3)封装系列-内存管理的封装,内存的复用
目录 前言1. 内存管理封装2. 补充知识总结 前言 杜老师推出的 tensorRT从零起步高性能部署 课程,之前有看过一遍,但是没有做笔记,很多东西也忘了。这次重新撸一遍,顺便记记笔记。 本次课程学习 tensorRT 高级-内存管理的封装&…...

Keepalived入门指南:实现故障转移和负载均衡
文章目录 一、简介1. Keepalived概述2. 高可用性和负载均衡的重要性 二、故障转移1. 什么是故障转移2. Keepalived的故障转移原理a) VRRP协议b) 虚拟路由器ID和优先级 3. 配置Keepalived实现故障转移a) 主备服务器的设置b) 监控网络接口c) 虚拟IP的配置d) 备份服务器接管流程 三…...

cuOSD(CUDA On-Screen Display Library)库的学习
目录 前言1. cuOSD1.1 Description1.2 Getting started1.3 For Python Interface1.4 Demo1.5 Performance Table 2. cuOSD案例2.1 环境配置2.2 simple案例2.3 segment案例2.4 segment2案例2.5 polyline案例2.6 comp案例2.7 perf案例 3. cuOSD浅析3.1 simple_draw函数 4. 补充知…...

c++函数指针基本用法
将函数像变量一样传递,实际上拿到的是函数的地址,由于函数类型的多样,可以使用auto关键字,可以使用 void(*function2)() ,不过它太繁琐,因此使用typedef 起个名字 typedef void(*HelloWorldFunction)(); 叫…...

Java创建对象的几种方式
在Java中,对象是程序中的一种基本元素,它通过类定义和创建。本篇教程旨在介绍Java中创建对象的几种方式,包括使用new关键字、反射、clone、反序列化等方式。 使用new关键字创建对象 在Java中,最常用的创建对象方式是使用new关键…...

Docker实战专栏简介
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
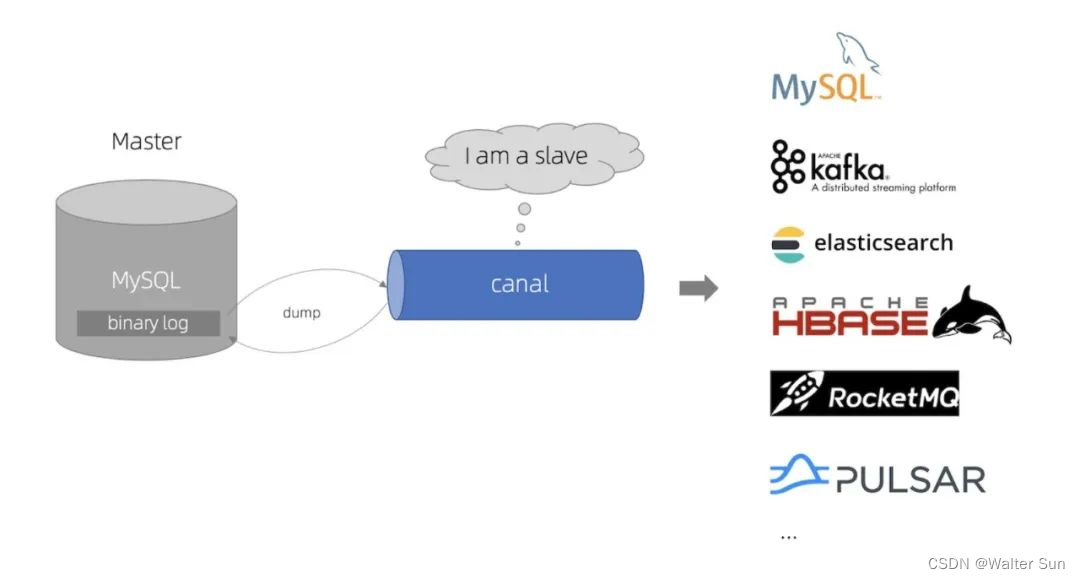
解放数据库,实时数据同步利器:Alibaba Canal
文章首发地址 Canal是一个开源的数据库增量订阅&消费组件,主要用于实时数据同步和数据订阅的场景,特别适用于构建分布式系统、数据仓库、缓存更新等应用。它支持MySQL、阿里云RDS等主流数据库,能够实时捕获数据库的增删改操作ÿ…...

机器学习基础之《分类算法(3)—模型选择与调优》
作用是如何选择出最好的K值 一、什么是交叉验证(cross validation) 1、定义 交叉验证:将拿到的训练数据,分为训练和验证集。以下图为例:将数据分成5份,其中一份作为验证集。然后经过5次(组)的测试&#x…...
Datawhale Django后端开发入门 TASK03 QuerySet和Instance、APIVIew
一、QuerySet QuerySet 是 Django 中的一个查询集合,它是由 Model.objects 方法返回的,并且可以用于生成数据库中所有满足一定条件的对象的列表。 QuerySet 在 Django 中表示从数据库中获取的对象集合,它是一个可迭代的、类似列表的对象集合。主要特点…...

Python 网页解析中级篇:深入理解BeautifulSoup库
在Python的网络爬虫中,BeautifulSoup库是一个重要的网页解析工具。在初级教程中,我们已经了解了BeautifulSoup库的基本使用方法。在本篇文章中,我们将深入学习BeautifulSoup库的进阶使用。 一、复杂的查找条件 在使用find和find_all方法查找…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
