数据结构<树和二叉树>顺序表存储二叉树实现堆排

✨Blog:🥰不会敲代码的小张:)🥰
🉑推荐专栏:C语言🤪、Cpp😶🌫️、数据结构初阶💀
💽座右铭:“記住,每一天都是一個新的開始😁😁😁”
💀本章内容:《树和二叉树》的介绍✨
1.树的概念及结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的
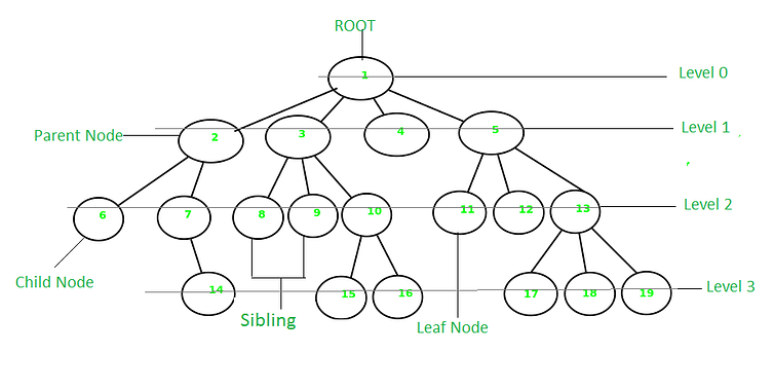
树形结构中,子树之间不能有交集,否则就不是树形结构
目录
- 1.树的概念及结构
- 树的表示
- 树在实际中的运用
- 2.二叉树概念及结构
- 满二叉树和完全二叉树
- 二叉树的存储结构
- 二叉树顺序表存储
- 3.堆的概念
- 用顺序存储完成堆的实现
- 创捷堆需要的结构
- 初始化
- 销毁堆
- 交换两个数
- 向上调整
- 插入
- 向下调整
- 删除
- 返回堆顶
- 判空
- 堆的大小
树的表示
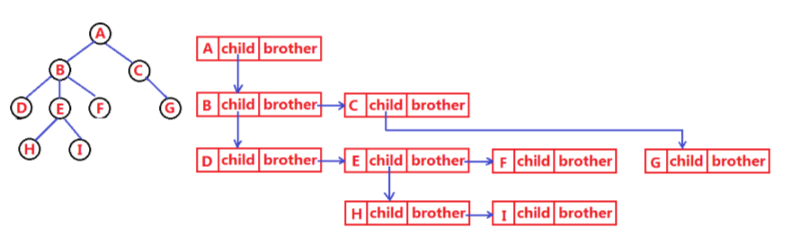
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextSibling; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
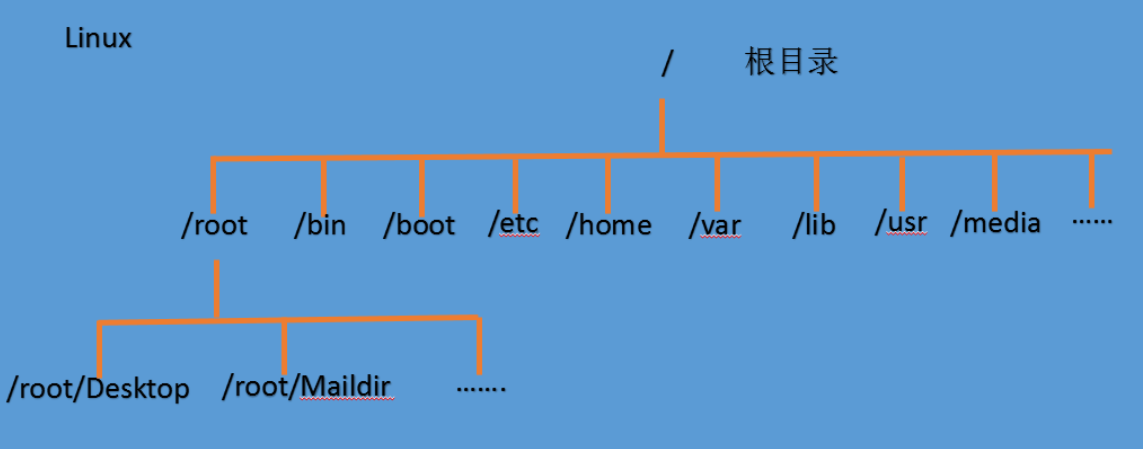
树在实际中的运用
下图可以看得出Linux使用的就是树形结构,父亲节点可以有n个孩子
2.二叉树概念及结构
一棵二叉树是结点的一个有限集合,该集合:
1.或者为空
2.由一个根节点加上两棵别称为左子树和右子树的二叉树组成
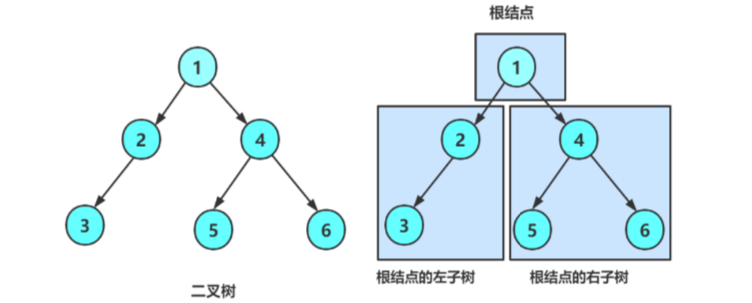
从上图可以看出:
1.二叉树不存在度大于2的结点
2.二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
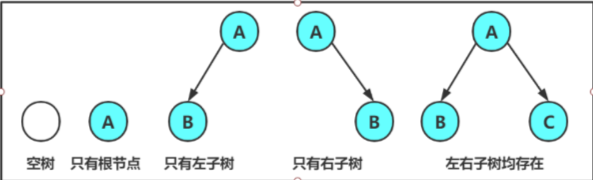
满二叉树和完全二叉树
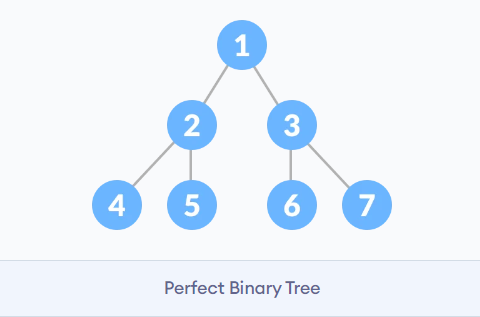
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
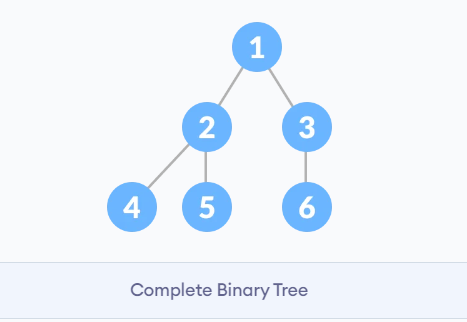
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
二叉树顺序表存储
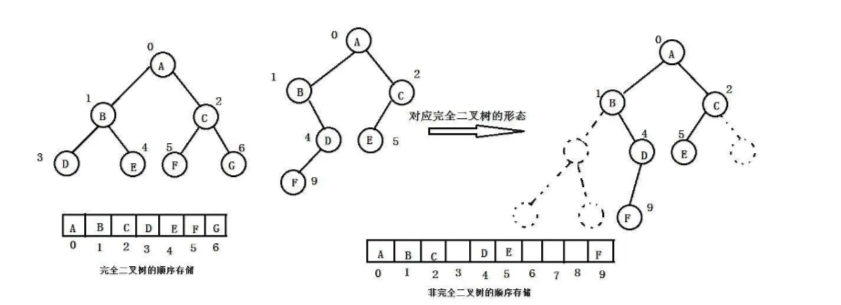
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
顺序表存储二叉树,只适用于完全二叉树否则会有空间上的浪费
3.堆的概念
如果有一个关键码的集合,把它的所有元素按完全二叉树的顺序存储方式存储,在一个一维数组中,将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
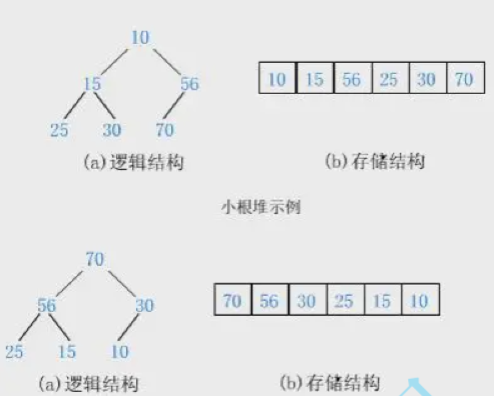
用顺序存储完成堆的实现
一个数组,我们可以看作一个二叉树,但还不是堆,所以使用向上/下调整成一个堆。
- 建堆
升序:建大堆
降序:建小堆 - 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
表示二叉树的值在数组位置中父子的下标关系
parent = (child-1)/2
leftchild = parent * 2 +1
rightchild = parent * 2 +2
创捷堆需要的结构
typedef int HpDatatype;
typedef struct Heap
{HpDatatype* data;//元素int size;//长度int capcity;//容量
}Heap;
初始化
//初始化
void HeapInit(Heap* php)
{assert(php);php->data = (HpDatatype*)malloc(sizeof(HpDatatype) * 4);if (php->data == NULL){perror("malloc fail");return;}php->size = 0;php->capcity = 4;}
销毁堆
//销毁堆
void HeapDestroy(Heap* php)
{assert(php);free(php->data);php->data = NULL;php->size = 0;php->capcity = 0;}
交换两个数
//交换两个数
void Swap(HpDatatype* p1, HpDatatype* p2)
{HpDatatype tmp = *p1;*p1 = *p2;*p2 = tmp;
}
向上调整
时间复杂度:N*logN
//向上调整
void AdjustUp(HpDatatype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
插入
//插入
void HeapPush(Heap* php, HpDatatype x)
{assert(php);if (php->capcity == php->size){HpDatatype* tmp = (HpDatatype*)realloc(php->data, sizeof(HpDatatype) * php->capcity * 2);if (tmp == NULL){perror("malloc fail");return;}php->data = tmp;php->capcity *= 2;}php->data[php->size] = x;php->size++;AdjustUp(php->data, php->size-1);
}
向下调整
时间复杂度:O(N)
//向下调整
void AdjustDown(HpDatatype* a, int n, int parent)
{int child = parent * 2 + 1;if (child+1 < n && a[child] < a[child + 1]){child++;}while (child < n){if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
删除
//删除
void HeapPop(Heap* php)
{assert(php);//assert(!HeapEmpty(php->data));Swap(&php->data[0], &php->data[php->size - 1]);php->size--;AdjustDown(php->data, php->size, 0);
}
返回堆顶
//返回堆顶
HpDatatype HeapTop(Heap* php)
{assert(php);return php->data[0];
}
判空
//判空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}
堆的大小
//堆的大小
int HeapSize(Heap* php)
{return php->size;
}
相关文章:

数据结构<树和二叉树>顺序表存储二叉树实现堆排
✨Blog:🥰不会敲代码的小张:)🥰 🉑推荐专栏:C语言🤪、Cpp😶🌫️、数据结构初阶💀 💽座右铭:“記住,每一天都是一個新的開始…...

理解docker命令
基础命令 帮助命令 docker --help(帮助命令) 用于获取某个命令的帮助信息 #命令帮助 docker 命令 --help 小技巧 换行符 \ 使用命令换符,可以让繁杂命令变得有条理 #命令换行,使用换行符 \ docker ... \... \ 镜像命令 d…...
线程函数 tp_recv_thread 源码分析)
【SA8295P 源码分析】16 - QNX侧 TouchScreen Panel (TP)线程函数 tp_recv_thread 源码分析
【SA8295P 源码分析】16 - QNX侧 TouchScreen Panel (TP)线程函数 tp_recv_thread 源码分析 一、TP 线程函数:tp_recv_thread()二、处理&上报 坐标数据 cypress_read_touch_data()系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P…...

第九章MyBatis的技巧
${}和#{}的区别 #{}给sql语句的占位符传值${}直接将值拼接到sql语句上,存在sql注入的现象 什么时候用${} 需要先对sql语句拼接,然后再编译。 字符串排序字段向SQL语句中拼接表名。比如根据日期生成日志表 批量删除 delete from car where in(${ids}…...

计算机技术与软件专业技术资格(水平)考试----系统架构设计师
【原文链接】计算机技术与软件专业技术资格(水平)考试----系统架构设计师 考试简介 计算机软件资格考试是由国家人力资源和社会保障部、工业和信息化部领导下的国家级考试。计算机软件资格考试既是职业资格考试,又是职称资格考试。考试合格…...

使用nrm快速切换npm源以及解决Method Not Implemented
文章目录 什么是nrm如何使用nrm查看本机目前使用的npm 源安装nrm查看可选源查看当前使用源切换源添加源删除源测试源的响应时间 如果你遇到这个报错,就可以采用这种方案解决哦解决方案:1. 切换为官方源2. 查看漏洞3. 修复漏洞4. 下面命令慎重使用&#x…...

NVIDIA Jetson 项目:机器人足球比赛
推荐:使用 NSDT场景编辑器 助你快速搭建可二次编辑器的3D应用场景 事实上,整个比赛都致力于这个想法。RoboCup小型联盟(SSL)视觉停电技术挑战赛鼓励团队“探索本地传感和处理,而不是非车载计算机和全球摄像机感知环境的…...
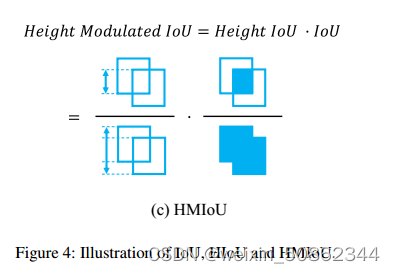
【论文解读】Hybrid-SORT: Weak Cues Matter for Online Multi-Object Tracking
因为Hybrid-SORT的baseline是基于OCSORT进行改进的,在这之前建议先了解byteTrack和【】的相关知识 1.介绍 1.1 基本框架 多目标跟踪(MOT)将问题分为两个子任务。第一个任务是检测每个帧中的对象。第二个任务是将它们在不同的框架中联系起来。关联任务主要通过显式…...
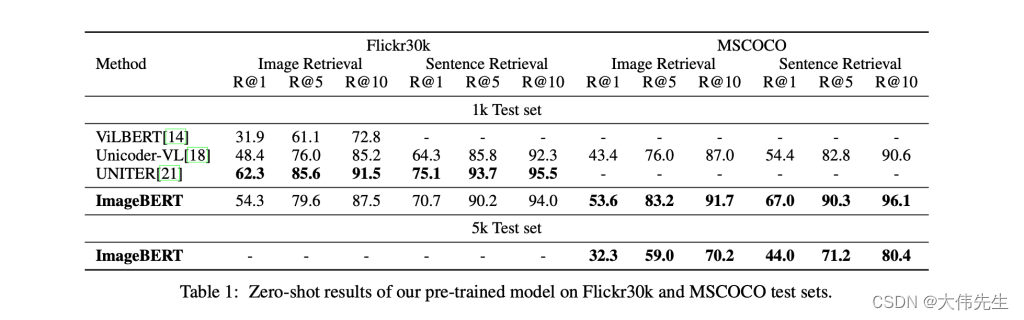
Microsoft 图像BERT,基于大规模图文数据的跨模态预训练
视觉语言任务是当今自然语言处理(NLP)和计算机视觉领域的热门话题。大多数现有方法都基于预训练模型,这些模型使用后期融合方法融合下游任务的多模态输入。然而,这种方法通常需要在训练期间进行特定的数据注释,并且对于…...

vue3+elementUI-plus实现select下拉框的虚拟滚动
网上查了几个方案,要不就是不兼容,要不就是不支持vue3, 最终找到一个合适的,并且已上线使用,需要修改一下样式: 代码如下: main.js里引用 import vue3-virtual-scroller/dist/vue3-virtual-scroller.css; …...
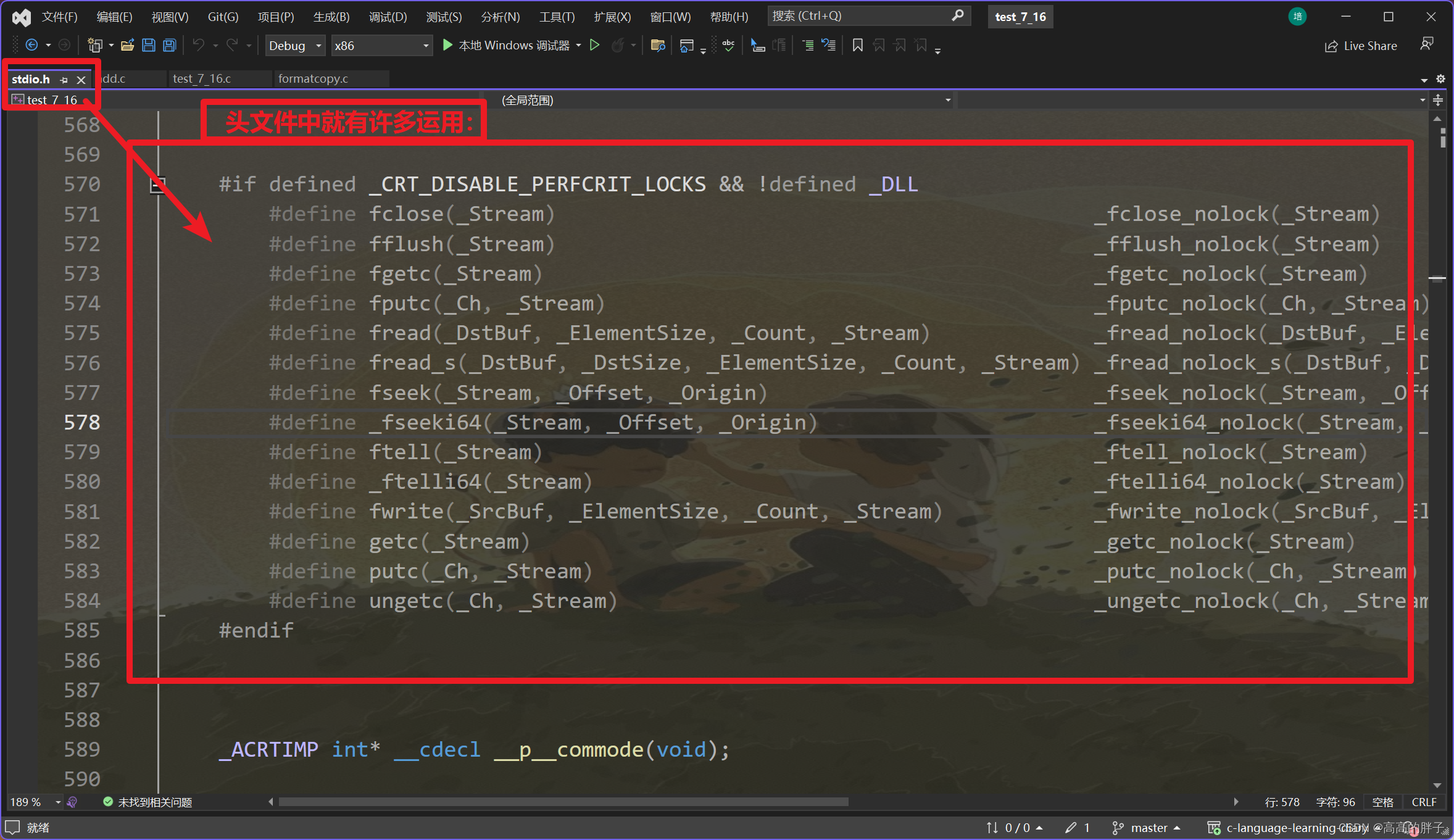
学C的第三十四天【程序环境和预处理】
相关代码gitee自取: C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第三十三天【C语言文件操作】_高高的胖子的博客-CSDN博客 1 . 程序的翻译环境和执行环境 在ANSI C(C语言标准)的任何一种实现中,存在两个不同的环境。 ࿰…...
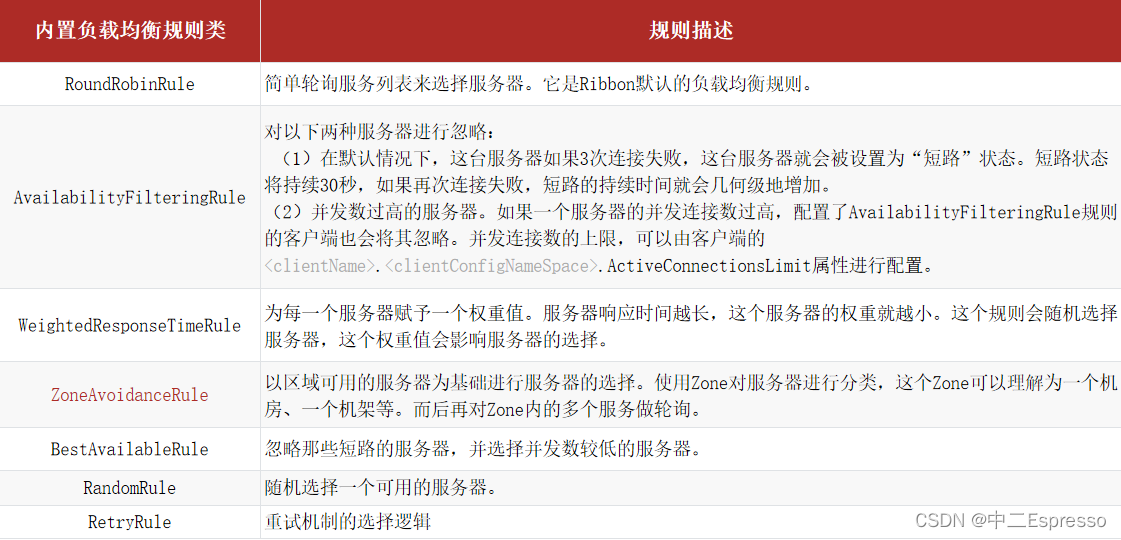
微服务中间件--Ribbon负载均衡
Ribbon负载均衡 a.Ribbon负载均衡原理b.Ribbon负载均衡策略 (IRule)c.Ribbon的饥饿加载 a.Ribbon负载均衡原理 1.发起请求http://userservice/user/1,Ribbon拦截该请求 2.Ribbon通过EurekaServer拉取userservice 3.EurekaServer返回服务列表给Ribbon做负载均衡 …...

字符设备驱动实例(ADC驱动)
四、ADC驱动 ADC是将模拟信号转换为数字信号的转换器,在 Exynos4412 上有一个ADC,其主要的特性如下。 (1)量程为0~1.8V。 (2)精度有 10bit 和 12bit 可选。 (3)采样时钟最高为5MHz,转换速率最高为1MSPS (4)具有四路模拟输入,同一时…...
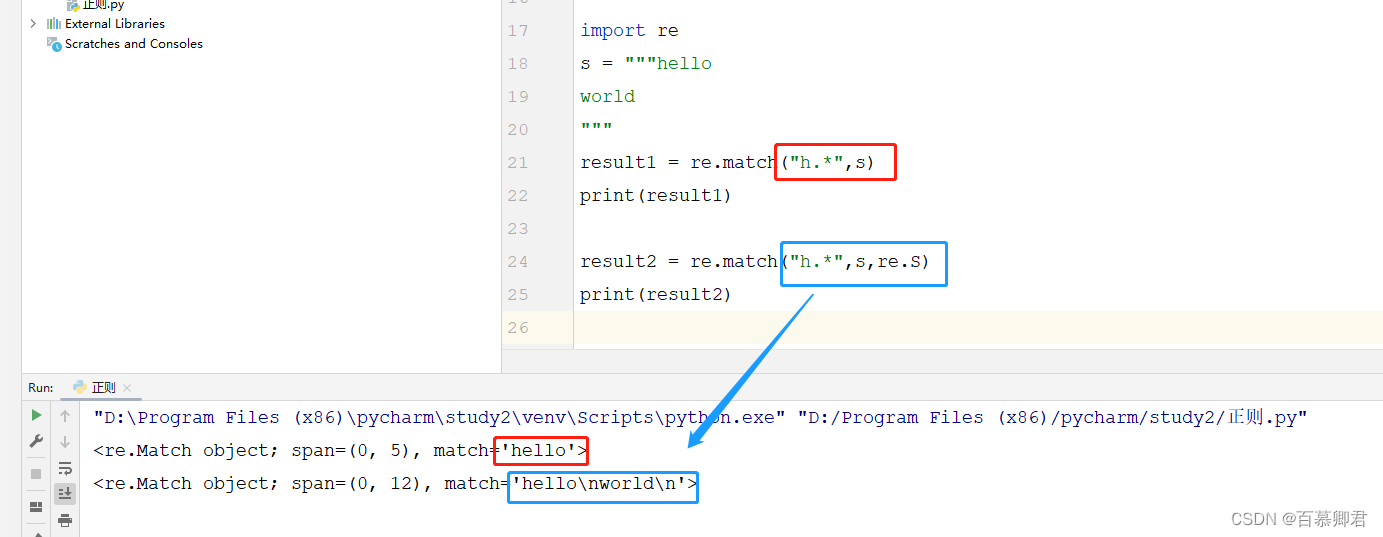
python基础5——正则、数据库操作
文章目录 一、数据库编程1.1 connect()函数1.2 命令参数1.3 常用语句 二、正则表达式2.1 匹配方式2.2 字符匹配2.3 数量匹配2.4 边界匹配2.5 分组匹配2.6 贪婪模式&非贪婪模式2.7 标志位 一、数据库编程 可以使用python脚本对数据库进行操作,比如获取数据库数据…...

SpringAOP原理:手写动态代理实现
0、基础知识 AOP我们知道,是在不修改源代码的情况下,为代码添加一些新功能的技术。通过动态代理,可以在不修改原始类代码的前提下,对方法进行拦截和增强。 动态代理常用于在不改变原有业务逻辑的情况下,对方法…...
【旅游度假】Axure酒店在线预订APP原型图 旅游度假子模块原型模板
作品概况 页面数量:共 10 页 兼容软件:Axure RP 9/10,不支持低版本 应用领域:旅游度假,生活服务 作品申明:页面内容仅用于功能演示,无实际功能 作品特色 本作品为「酒店在线预订」的移动端…...

Android JNI系列详解之CMake和ndk-build编译工具介绍
一、前提 CMake和ndk-build只是编译工具,本次主要介绍ndk-build和CMake的区别,下节课介绍他们的使用。 二、CMake工具介绍 CMake:cross platform make,是跨平台的编译工具 CMake是在AndroidStudio2.2之后引入(目前默认…...

【Linux取经路】解析环境变量,提升系统控制力
文章目录 一、进程优先级1.1 什么是优先级?1.2 为什么会有优先级?1.3 小结 二、Linux系统中的优先级2.1 查看进程优先级2.2 PRI and NI2.3 修改进程优先级2.4 进程优先级的实现原理2.5 一些名词解释 三、环境变量3.1 基本概念3.2 PATH:Linux系…...
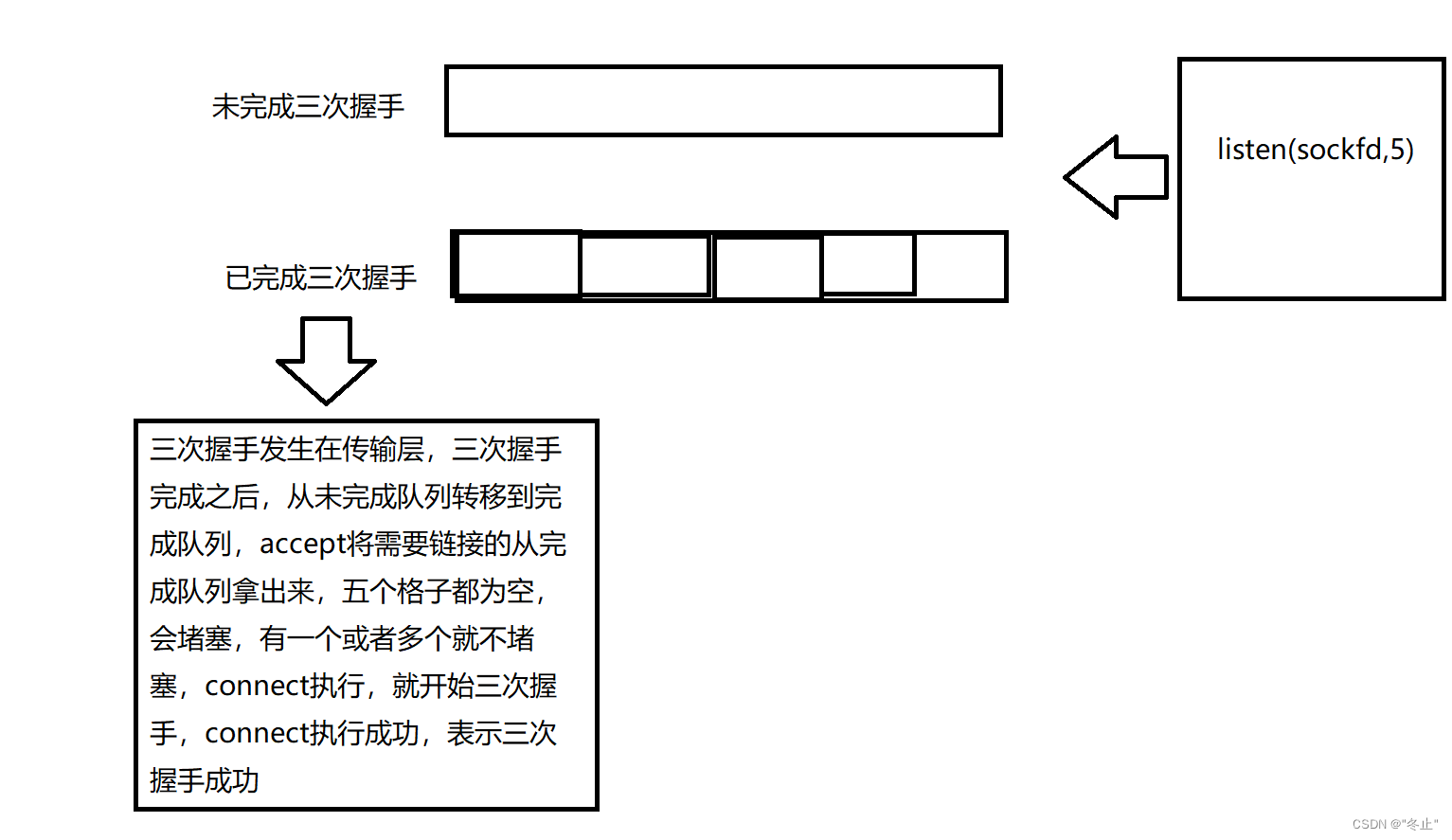
TCP编程流程(补充)
目录 1、listen: 2、listen、tcp三次握手 3、 发送缓冲区和接收缓冲区: 4、tcp编程启用多线程 1、listen: 执行listen会创建一个监听队列 listen(sockfd,5) 2、listen、tcp三次握手 三次握手 3、 发送缓冲区和接收缓冲区:…...
每天一道leetcode:433. 最小基因变化(图论中等广度优先遍历)
今日份题目: 基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 A、C、G 和 T 之一。 假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。 例如,&quo…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
