CNN卷积详解(三)
一、卷积层的计算
4 ∗ * ∗ 4的输入矩阵 I I I 和 3 ∗ * ∗ 3 的卷积核 K K K:
- 在步长(stride)为 1 时,输出的大小为 ( 4 − 3 + 1 ) × ( 4 − 3 + 1)
计算公式:
● 输入图片矩阵 I I I 大小: w × w w × w w×w
● 卷积核 K K K: k × k k × k k×k
● 步长 S S S: s s s
● 填充大小(padding): p p p
o = ( w − k + 2 p ) s + 1 o = \frac{(w − k + 2p )}{s}+1 o=s(w−k+2p)+1
输出图片大小为: o × o o × o o×o
● 步长为2,卷积核为33,p=0的卷积情况如下:

当卷积函数中padding='same’时,会动态调整 p p p 值,确保 o = w o = w o=w ,即保证输入与输出一致。例如:输入是 28281 输出也为 28281 。
● 步长为1,卷积核为33,padding='same’的卷积情况如下:

🔍实例:
7 ∗ 7 7*7 7∗7 的 input, 3 ∗ 3 3*3 3∗3 的 kernel,无填充(padding=0),步长为1,则 o = ( 7 − 3 ) 1 + 1 o = \frac{(7 − 3 )}{1}+1 o=1(7−3)+1也即 output size 为 5 ∗ 5 5*5 5∗5

7 ∗ 7 7*7 7∗7 的 input, 3 ∗ 3 3*3 3∗3 的 kernel,无填充(padding=0),步长为2,则 o = ( 7 − 3 ) 2 + 1 o = \frac{(7 − 3 )}{2}+1 o=2(7−3)+1也即 output size 为 3 ∗ 3 3*3 3∗3

二、卷积层运算量的计算

对于第一个卷积过程涉及的计算量计算过程如下:
首先,我们需要计算卷积层的参数量。对于一个卷积核大小为 k × k k \times k k×k,输入特征图大小为 h × w × c i n h \times w \times c_{in} h×w×cin,输出特征图大小为 h ′ × w ′ × c o u t h' \times w' \times c_{out} h′×w′×cout的卷积层,其参数量为:
𝑃𝑎𝑟𝑎𝑚 = k 2 × c i n × c o u t k^2 \times c_{in} \times c_{out} k2×cin×cout + c o u t c_{out} cout
其中最后的 c o u t c_{out} cout是bias的数量
引自: [假设卷积核的大小为 k*k, 输入channel为M, 输出channel为N。]
(1)bias为True时:参数数量为: k × k × M × N + N k × k × M × N + N k×k×M×N+N (bias的数量与输出channel的数量是一样的)(2)bias为False时:参数数量为: k × k × M × N k×k×M×N k×k×M×N
(3)当使用BN时,还有两个可学习的参数α和β,参数量均为N 则参数数量为: k × k × M × N + 3 × N k×k×M×N + 3×N k×k×M×N+3×N
对于本题,输入特征图大小为 100 × 100 × 128 100 \times 100 \times 128 100×100×128,输出特征图大小为 100 × 100 × 256 100 \times 100 \times 256 100×100×256,卷积核大小为 5 × 5 5 \times 5 5×5,且填充为 2,步长为 1,输出通道数为 256。因此,每个卷积层的参数量为:
𝑃𝑎𝑟𝑎𝑚 = 5 2 × 128 × 256 5^2 \times 128 \times 256 52×128×256 + 256 ≈ 8.192 × 1 0 5 8.192 \times 10^5 8.192×105
参数量会计算了,那么 F L O P s FLOPs FLOPs其实也是很简单的,就一个公式:
F L O P s t o t a l FLOPs_{total} FLOPstotal = 𝑃𝑎𝑟𝑎𝑚 × h ′ × w ′ \times h' \times w' ×h′×w′ = 8.192 × 1 0 5 × 100 × 100 8.192 \times 10^5 \times 100 \times 100 8.192×105×100×100= 8.192 × 1 0 9 8.192 \times 10^9 8.192×109
因此,经过具有 256 个输出的 5x5 卷积层之后,输出数据为 100x100x256 的计算量是约为 8.192 × 1 0 9 F L O P s 8.192 \times 10^{9} FLOPs 8.192×109FLOPs。
对于第二个卷积过程涉及的计算量计算过程如下:
首先考虑 1x1 卷积层的计算量。套用上面的公式,输入特征图大小为 100 × 100 × 128 100 \times 100 \times 128 100×100×128,输出通道数为 32,因此经过 1x1 卷积层后,输出特征图大小为 100 × 100 × 32 100 \times 100 \times 32 100×100×32,这里的bias值很小我直接省了,计算量为:
F L O P s 1 × 1 FLOPs_{1\times1} FLOPs1×1 = 1 2 × 128 × 32 × 100 × 100 = 4.096 × 1 0 7 1^2 \times 128 \times 32 \times 100 \times 100 = 4.096 \times 10^7 12×128×32×100×100=4.096×107
接下来考虑 5x5 卷积层的计算量,经过 1x1 卷积层后,输出特征图大小为 100 × 100 × 32 100 \times 100 \times 32 100×100×32,输入通道数为 32,输出通道数为 256,卷积核大小为 5x5,填充为 2,步长为 1,这里的bias值很小我直接省了,计算量为:
F L O P s 5 × 5 FLOPs_{5\times5} FLOPs5×5 = 5 2 × 32 × 256 × 100 × 100 = 2.048 × 1 0 9 5^2 \times 32 \times 256 \times 100 \times 100= 2.048 \times 10^{9} 52×32×256×100×100=2.048×109
因此,经过具有 32 个 1x1大小的卷积核的卷积层和具有 256 个5x5大小的卷积核的卷积层之后,输出数据为 100x100x256 的计算量为
F L O P s 1 × 1 + F L O P s 5 × 5 FLOPs_{1\times1} + FLOPs_{5\times5} FLOPs1×1+FLOPs5×5 ≈ 2.048 × 1 0 9 2.048 \times 10^{9} 2.048×109
相关文章:

CNN卷积详解(三)
一、卷积层的计算 4 ∗ * ∗ 4的输入矩阵 I I I 和 3 ∗ * ∗ 3 的卷积核 K K K: 在步长(stride)为 1 时,输出的大小为 ( 4 − 3 1 ) ( 4 − 3 1) 计算公式: ● 输入图片矩阵 I I I 大小: w w w w ww ●…...

使用 Amazon Redshift Serverless 和 Toucan 构建数据故事应用程序
这是由 Toucan 的解决方案工程师 Django Bouchez与亚马逊云科技共同撰写的特约文章。 带有控制面板、报告和分析的商业智能(BI,Business Intelligence)仍是最受欢迎的数据和分析使用场景之一。它为业务分析师和经理提供企业的过去状态和当前状…...

CentOS 上快速安装包管理工具Conda
要在 CentOS 上安装 Conda,您可以按照以下步骤进行操作: 1. 下载 Miniconda 或 Anaconda 安装脚本: Miniconda:适用于轻量级安装的 Miniconda 版本。 wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.…...
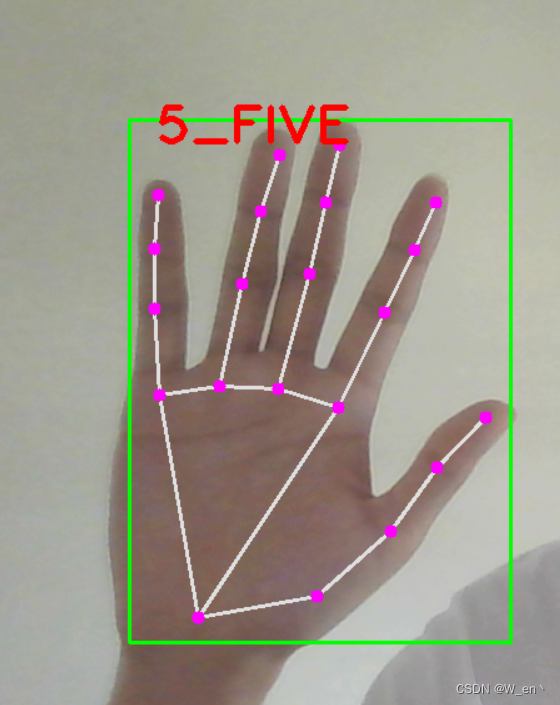
opencv-手势识别
# HandTrackingModule.py import cv2 import mediapipe as mpclass HandDetector:"""使用mediapipe库查找手。导出地标像素格式。添加了额外的功能。如查找方式,许多手指向上或两个手指之间的距离。而且提供找到的手的边界框信息。"""…...
qcdisplaycfg_ADP_STAR_LA.xml 配置文件解析)
【SA8295P 源码分析】10 - HQX Display(OpenWFD)qcdisplaycfg_ADP_STAR_LA.xml 配置文件解析
【SA8295P 源码分析】10 - HQX Display(OpenWFD)qcdisplaycfg_ADP_STAR_LA.xml 配置文件解析 一、HQX Display 介绍1.1 OpenWF Display Driver二、HQX Display 配置文件参数解析2.1 qcdisplaycfg.xml 配置文件2.1 配置两个 DPUs in QNX2.1.1 配置 graphics_ADP_STAR.conf : …...

达梦数据库权限和预定角色介绍
概述 本文对达梦数据库数据库和对象权限及DM预定义角色及角色创建进行介绍。 1.权限管理 用户权限有两类:数据库权限和对象权限。 数据库权限主要是指针对数据库对象的创建、删除、修改的权限,对数据库备份等权限。 数据库权限一般由 SYSDBA、SYSAU…...
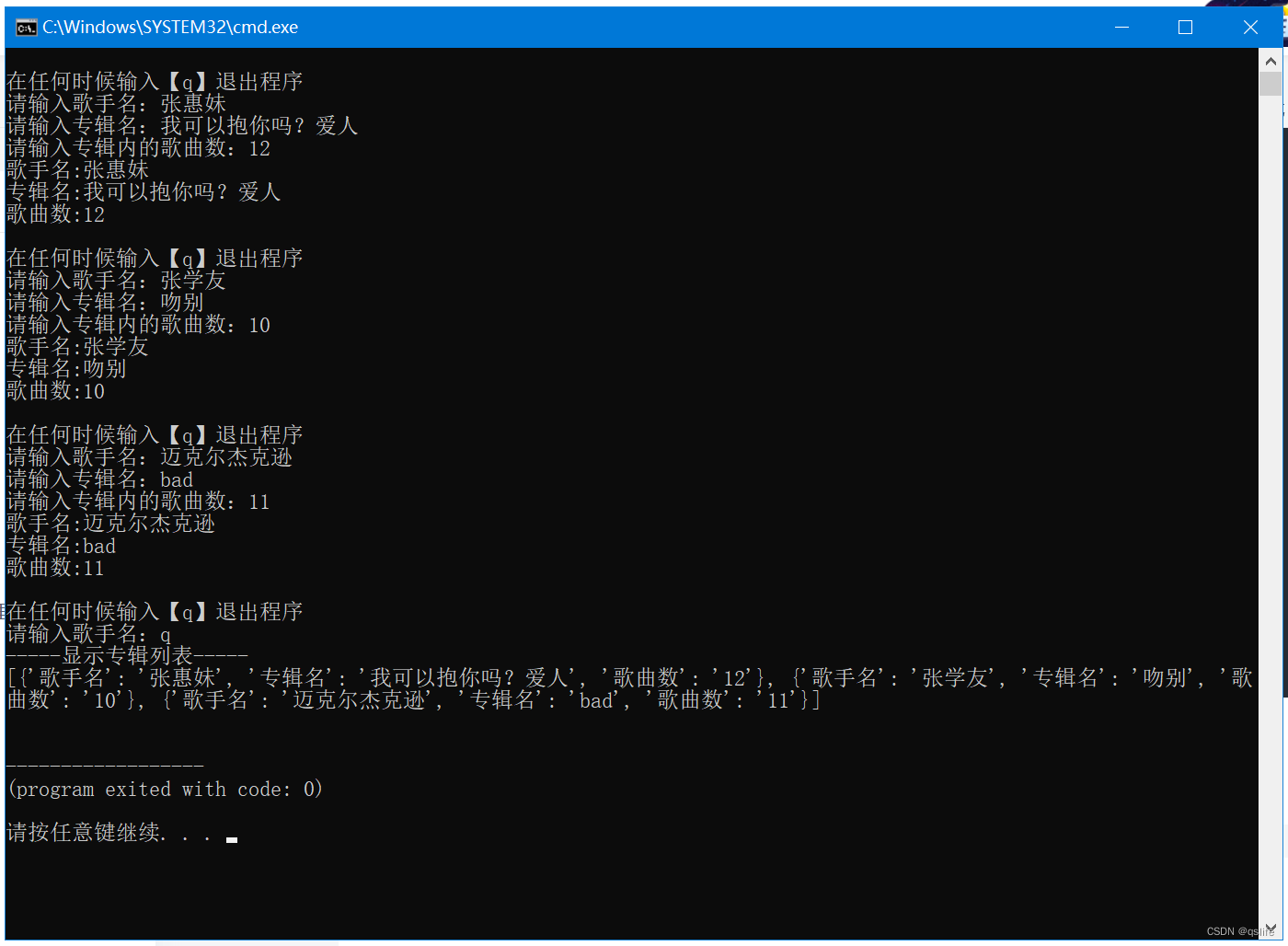
Python编程从入门到实践_8-8 用户的专辑_答案
Python编程从入门到实践_8-8 用户的专辑_答案 我也看了一些其他人的答案,很多的答案存在问题,每次调用函数 make_album() 后生成一个专辑字典会覆盖上次调用函数 make_album() 生成的字典,不符合题意。 我采取的解决方案是添加一个空列表 …...

HummingBird 基于 Go 开源超轻量级 IoT 物联网平台
蜂鸟(HummingBird) 是 Go 语言实现的超轻量级物联网开发平台,包含设备接入、产品管理、物模型、告警中心、规则引擎等丰富功能模块。系统采用GoLang编写,占用内存极低, 单物理机可实现百设备的连接。 在数据存储上&…...

10.小程序样式
样式 css部分样式不支持,并且添加了rpx属性,小程序开发的时候应该使用rpx,而不是px,因为rpx是将移动端的屏幕大小分为750份,会自动按设备的大小去适配;我们在开发时应该以iphone6为基准的设备进行开发&…...
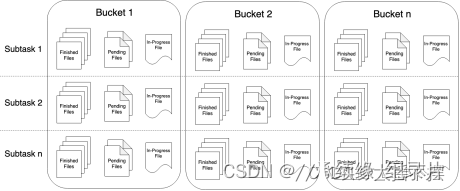
Flink 流式读写文件、文件夹
文章目录 一、flink 流式读取文件夹、文件二、flink 写入文件系统——StreamFileSink三、查看完整代码 一、flink 流式读取文件夹、文件 Apache Flink针对文件系统实现了一个可重置的source连接器,将文件看作流来读取数据。如下面的例子所示: StreamExe…...

【SA8295P 源码分析】64 - QNX 与 Android GVM 显示 Dump 图片方法汇总
【SA8295P 源码分析】64 - QNX 与 Android GVM 显示 Dump 图片方法汇总 一、QNX侧1.1 surfacedump 功能1.2 screenshot 功能二、Android GVM 侧2.1 screencap -p 导出 PNG 图片2.2 screencap 不加 -p 参数,导出 RGB32 图片2.3 dumpsys SurfaceFlinger --display-id 方法系列文…...

字符串旋转(1)
目录 编辑 题目要求😍: 题目内容❤: 题目分析📚: 主函数部分📕:编辑 方法一🐒: 方法二🐒🐒: 方法三🐒…...

【SA8295P 源码分析】13 - Android GVM 虚拟机 QUPv3 UART / SPI / I2C功能配置及透传配置
【SA8295P 源码分析】13 - Android GVM 虚拟机 QUPv3 UART / SPI / I2C功能配置及透传配置 一、QUP v3 介绍二、QUP v3 UART 功能配置2.1 TrustZone 域 Uart 资源权限配置:以 QUPV3_0_SE2 为例2.2 QNX Host 域关闭 Uart 资源:以 QUPV3_0_SE2 为例2.3 Android Kernel 域使能 U…...

STM32 F103C8T6学习笔记10:OLED显示屏GIF动图取模—简易时钟—动图手表的制作~
今日尝试做一款有动图的OLED实时时钟,本文需要现学一个OLED的GIF动图取模 其余需要的知识点有不会的可以去我 STM32 F103C8T6学习笔记 系列专栏自己查阅把,闲话不多,直接开肝~~~ 文章提供源码,测试工程下载,测试效…...
大数据课程K3——Spark的常用案例
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Spark的常用案例——WordCount; ⚪ 掌握Spark的常用案例——求平均值; ⚪ 掌握Spark的常用案例——求最大值和最小值; ⚪ 掌握Spark的常用案例——TopK; ⚪ 掌握Spark的常用案例…...

85-最大矩阵
题目 给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。 示例 1: 输入:matrix [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,…...

8.3 【C语言】通过指针引用数组
8.3.1 数组元素的指针 所谓数组元素的指针就是数组元素的地址。 可以用一个指针变量指向一个数组元素。例如: int a[10]{1,3,5,7,9,11,13,15,17,19}; int *p; p&a[0]; 引用数组元素可以用下标法,也可以用指针法…...

基于Flink CDC实时同步PostgreSQL与Tidb【Flink SQL Client模式下亲测可行,详细教程】
文章目录 一、PostgreSQL作为数据来源(source),由flink读取1.postgre安装与配置2.flink安装与配置3.flink cdc postgre配置3.1 postgre配置(for flink cdc)3.2 flink cdc postgres的jar包下载 4.flink cdc postgre测试…...
Vue-5.编译器Idea
Vue专栏(帮助你搭建一个优秀的Vue架子) Vue-1.零基础学习Vue Vue-2.Nodejs的介绍和安装 Vue-3.Vue简介 Vue-4.编译器VsCode Vue-5.编译器Idea Vue-6.编译器webstorm Vue-7.命令创建Vue项目 Vue-8.Vue项目配置详解 Vue-9.集成(.editorconfig、…...

qiuzhiji3
本篇想介绍一下慧与,这里的工作氛围和企业文化令人难忘,希望更多人了解它 也想探讨一下不同的文化铸就的不同企业,究竟有哪些差别。 本篇将从我个人角度出发描述慧与。 2022/3/16至2023/7/31 本篇初次写于2023年8月20日 说起来在毕业之前那段…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
