一文彻底理解时间复杂度和空间复杂度(附实例)
目录
- 1 P=NP?
- 2 时间复杂度
- 2.1 常数阶复杂度
- 2.2 对数阶复杂度
- 2.3 线性阶复杂度
- 2.4 平方阶复杂度
- 2.5 指数阶复杂度
- 2.6 总结
- 3 空间复杂度
1 P=NP?
P类问题(Polynomial)指在多项式时间内能求解的问题;NP类问题(Non-Deterministic Polynomial)指在多项式时间内能验证一个解的问题。

问题的归约(reduction)指将一个问题的求解等效为另一个问题的求解,其中这种等效具有提升普遍性、加大复杂度的趋势,且问题归约可传递。举例而言,可以将求解一元一次方程归约为求解一元二次方程。
若任意一个NP类问题都能在多项式时间内归约到某个NP问题,则该问题被称为NP完全问题(NP-Complete);若无法归约到某个NP问题,则该问题被称为NP难问题(NP-Hard)。
P类问题本身是NP的,因为能在多项式时间内求解必然能在多项式时间内验证解。但反之,NP问题是否是P问题的论断称为“P=NP?”,该论断被列为千禧七大难题之首,暂未被证明或证伪。
2 时间复杂度
一般地,算法中基本操作重复执行的次数是问题规模 n n n的某个函数 f ( n ) f(n) f(n)。在计算机科学中用时间复杂度(Time Complexity)定性描述一个算法的运行时耗——体现在问题规模 n n n变化 c c c倍后算法的执行效率,而非针对一个特定的 n n n,记为
T ( n ) = O ( f ( n ) ) T\left( n \right) =O\left( f\left( n \right) \right) T(n)=O(f(n))
其中 O ( ⋅ ) O\left( \cdot \right) O(⋅)是复杂度度量函数,不包括输入的低阶项和首项系数(非常数项)。必须指出,使用 O ( ⋅ ) O\left( \cdot \right) O(⋅)属于渐进时间复杂度——输入值大小趋近无穷时的情况,否则不能忽略其他低阶项的影响。常见的时间复杂度如下
2.1 常数阶复杂度
常数阶复杂度记为 O ( a ) O(a) O(a)
示例:
// 计算 1 + 2 + 3 + ... + n 的值
int sum(int n)
{return (1 + n) * n / 2;
}
解释:对任意问题规模 ,算法均只执行一次,故认为算法时间复杂度为 O ( 1 ) O(1) O(1)
2.2 对数阶复杂度
常数阶复杂度记为 O ( log n ) O\left( \log n \right) O(logn)
示例:
/** 二分查找* A[] : 待查找的数组(已排序)* n : 数组长度* target : 查找的目标值*/
int binarySearch(int A[], int n, int target) {int lt = 0, rt = n;while(lt < rt){int mid = lt + (rt - lt)/2;if(A[mid] == target) return mid;else if(A[mid] > target) rt = mid;else lt = mid + 1;}return -1; // 查找不到
}
解释:二分查找算法每次迭代排除一半元素,因此第 m m m次迭代后剩余待查找元素个数为 n / 2 m {{n}/{2^m}} n/2m,最坏情况下排除到只剩最后一个值后得到结果——结果为该值或查找不到,即令 n / 2 m = 1 {{n}/{2^m}}=1 n/2m=1,则 f ( n ) = m = log 2 n f\left( n \right) =m=\log _2n f(n)=m=log2n,故认为算法时间复杂度为 O ( log n ) O\left( \log n \right) O(logn)
2.3 线性阶复杂度
示例:
// 计算 1 + 2 + 3 + ... + n 的值
int sum(int n)
{int sum = 0;for(int i = 1; i <= n; i++) {sum += i;}return sum
}
解释:对任意问题规模 n n n,算法均执行 n n n次,故认为算法时间复杂度为 O ( n ) O(n) O(n)
2.4 平方阶复杂度
示例:
/** 冒泡排序* arr[] : 待排序数组* n : 数组长度*/
void bubbleSort(int[] arr, int n) {if(n == 0 || n == 1) return;for(int i = 0; i < n - 1; ++i) {for(int j = 0; j < n - i - 1; ++j) {if(a[j] > a[j+1]) swap(a[j], a[j+1]);}}
}
解释:冒泡排序算法共 n − 1 n-1 n−1次迭代,每次迭代循环比较 n − i − 1 n-i-1 n−i−1次,故总迭代次数为 ( n − 1 ) + ( n − 2 ) + ⋯ + 1 = n ( n − 1 ) / 2 \left( n-1 \right) +\left( n-2 \right) +\cdots +1={{n\left( n-1 \right)}/{2}} (n−1)+(n−2)+⋯+1=n(n−1)/2,故认为算法时间复杂度为 O ( n 2 ) O\left( n^2 \right) O(n2)
2.5 指数阶复杂度
示例:
// 计算斐波那契数列
int fibonacci(int n)
{if (n<=0) return 0;if (n==1) return 1;return fb(n - 1) + fb(n - 2);
}
解释:斐波那契算法本质上是二阶常系数差分方程 f ( n ) = f ( n − 1 ) + f ( n − 2 ) f\left( n \right) =f\left( n-1 \right) +f\left( n-2 \right) f(n)=f(n−1)+f(n−2),其特征根为 x 1 , 2 = 1 ± 5 2 x_{1,2}=\frac{1\pm \sqrt{5}}{2} x1,2=21±5,则该差分方程通解为 f ( n ) = c 1 ( 1 + 5 2 ) n + c 2 ( 1 − 5 2 ) n f\left( n \right) =c_1\left( \frac{1+\sqrt{5}}{2} \right) ^n+c_2\left( \frac{1-\sqrt{5}}{2} \right) ^n f(n)=c1(21+5)n+c2(21−5)n,代入初始条件 f ( 0 ) = 0 f\left( 0 \right) =0 f(0)=0、 f ( 1 ) = 1 f\left( 1 \right) =1 f(1)=1解得 c 1 c_1 c1、 c 2 c_2 c2后即得
f ( n ) = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] f\left( n \right) =\frac{1}{\sqrt{5}}\left[ \left( \frac{1+\sqrt{5}}{2} \right) ^n-\left( \frac{1-\sqrt{5}}{2} \right) ^n \right] f(n)=51[(21+5)n−(21−5)n]
故认为算法时间复杂度为 O ( a n ) O\left( a^n \right) O(an)
2.6 总结
特别地,当 n n n处于复杂度底数位置时称为多项式时间复杂度,例如常数阶、对数阶、线性阶等;当 n n n处于复杂度指数位置时称为超多项式时间复杂度,例如指数阶、阶乘阶等。一般地,计算机只能处理多项式时间复杂度算法,而无法忍受超多项式时间算法中问题规模的些许增长带来的爆炸式耗时,因此将多项式时间视为算法在时间复杂度层面是否有效的分水岭,如图所示。
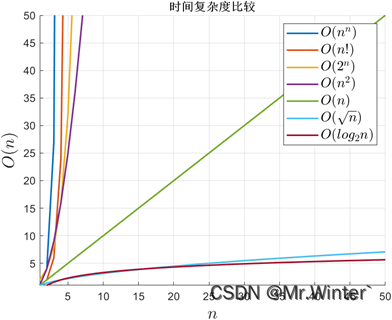
3 空间复杂度
在计算机科学中用空间复杂度(Space Complexity)定性描述一个算法的内存占用——体现在问题规模 n n n变化 c c c倍后算法临时占用内存的增长状况,而非针对一个特定的 n n n,记为
S ( n ) = O ( f ( n ) ) S\left( n \right) =O\left( f\left( n \right) \right) S(n)=O(f(n))
算法空间复杂度分析与时间复杂度类似,区别在于其关注的不是基础操作的重复次数,而是算法运行时堆栈中的内存消耗,在递归算法中尤为明显。一般地,算法复杂性分析优先考察时间复杂度,而假设空间不受限;对空间复杂度的考察主要集中在嵌入式领域。
下面是归并排序的实例。
/** 归并排序* a[] : 待排序数组* lt : 排序左索引* rt : 排序右索引* p[] : 临时数组,存储排序元素*/
void merge(int a[], int lt, int rt, int p[]){int mid = (rt - lt)/2 + lt;int i = lt, j = mid + 1;int k = 0;// 合并while(i <= mid && j <= rt){ if(a[i] <= a[j]) p[k++] = a[i++];else p[k++] = a[j++];}// 合并剩余while(i <= mid) p[k++] = a[i++];while(j <= rt) p[k++] = a[j++];// 重新赋值回去for(i = 0; i < k; ++i) a[lt+i] = p[i];
}// 划分
void mergeSort(int a[], int lt, int rt, int p[]){if(lt < rt){int mid = (rt - lt)/2 + lt;mergeSort(a, lt, mid, p); // 递归排序 lt ~ midmergeSort(a, mid+1, rt, p); // 递归排序 mid+1 ~ rtmerge(a, lt, rt, p); // 合并 lt ~ rt}
}
设问题规模为 n n n,即待排序元素为 n n n个,则递归调用时最坏情况下会产生 log 2 n \log _2n log2n层递归树。若临时数组在全局作用域中开辟,则递归过程中不再开辟新的内存空间,空间复杂度为 O ( n ) O(n) O(n);若临时数组在栈中申请,则每层递归都要开辟一次长度为 n n n的临时空间,空间复杂度为 O ( n log 2 n ) O\left( n\log _2n \right) O(nlog2n)
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

一文彻底理解时间复杂度和空间复杂度(附实例)
目录 1 PNP?2 时间复杂度2.1 常数阶复杂度2.2 对数阶复杂度2.3 线性阶复杂度2.4 平方阶复杂度2.5 指数阶复杂度2.6 总结 3 空间复杂度 1 PNP? P类问题(Polynomial)指在多项式时间内能求解的问题;NP类问题(Non-Deterministic Polynomial)指在…...
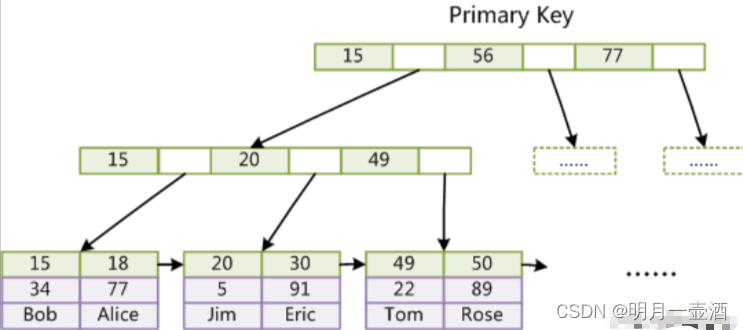
Mysql的索引详解
零. 索引类型概述 1. 实际开发中使用的索引种类 主键索引唯一索引普通索引联合索引全文索引空间索引 2. 索引的格式类型 BTree类型Hash类型FullText类型(全文索引)RTree类型(空间索引) MySQL 的索引方法,主要包括 BTREE 和 HASH。 顾名思…...

.netcore windows app启动webserver
创建controller: using Microsoft.AspNetCore.Mvc; using Microsoft.Extensions.Logging; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Text.Json.Serialization; using System.Threading.Tasks;namespace MyWorker.…...
泰迪大数据挖掘建模平台功能特色介绍
大数据挖掘建模平台面相高校、企业级别用户快速进行数据处理的建模工具。 大数据挖掘建模平台介绍 平台底层算法基于R语言、Python、Spark等引擎,使用JAVA语言开发,采用 B/S 结构,用户无需下载客户端,可直接通过浏览器进行…...

【问题】java序列化,什么时候使用
文章目录 是什么为什么如何做流操作 注事事项 是什么 把对象转换为字节序列的过程称为对象的序列化。 把字节序列恢复为对象的过程称为对象的反序列化。 对象的序列化主要有两种用途: 1)把对象的字节序列永久地保存到硬盘上,通常存放在一…...
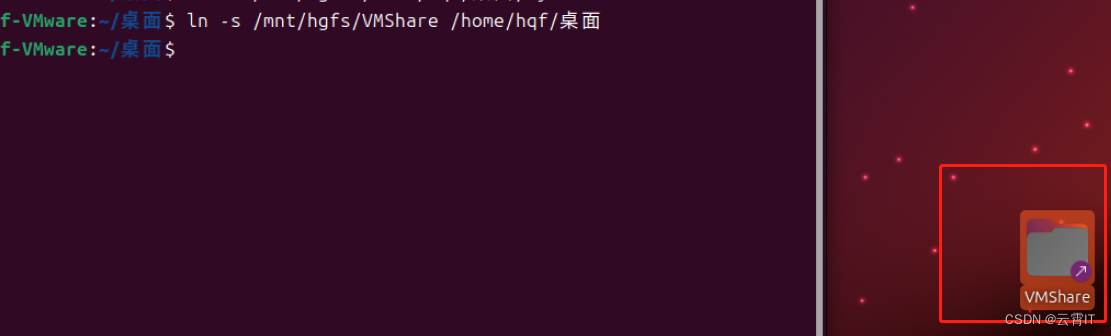
【最新可用】VMware中ubuntu与主机window之间使用共享文件夹传输大文件
一、VMware设置共享文件夹 (1)虚拟机关机情况下,创建一个共享文件夹 (2)ubuntu中挂载共享文件夹 1、如果之前已经挂载 hgfs,先取消挂载 sudo umount /mnt/hgfs2、重新使用以下命令挂载 sudo /usr/bin/vmh…...
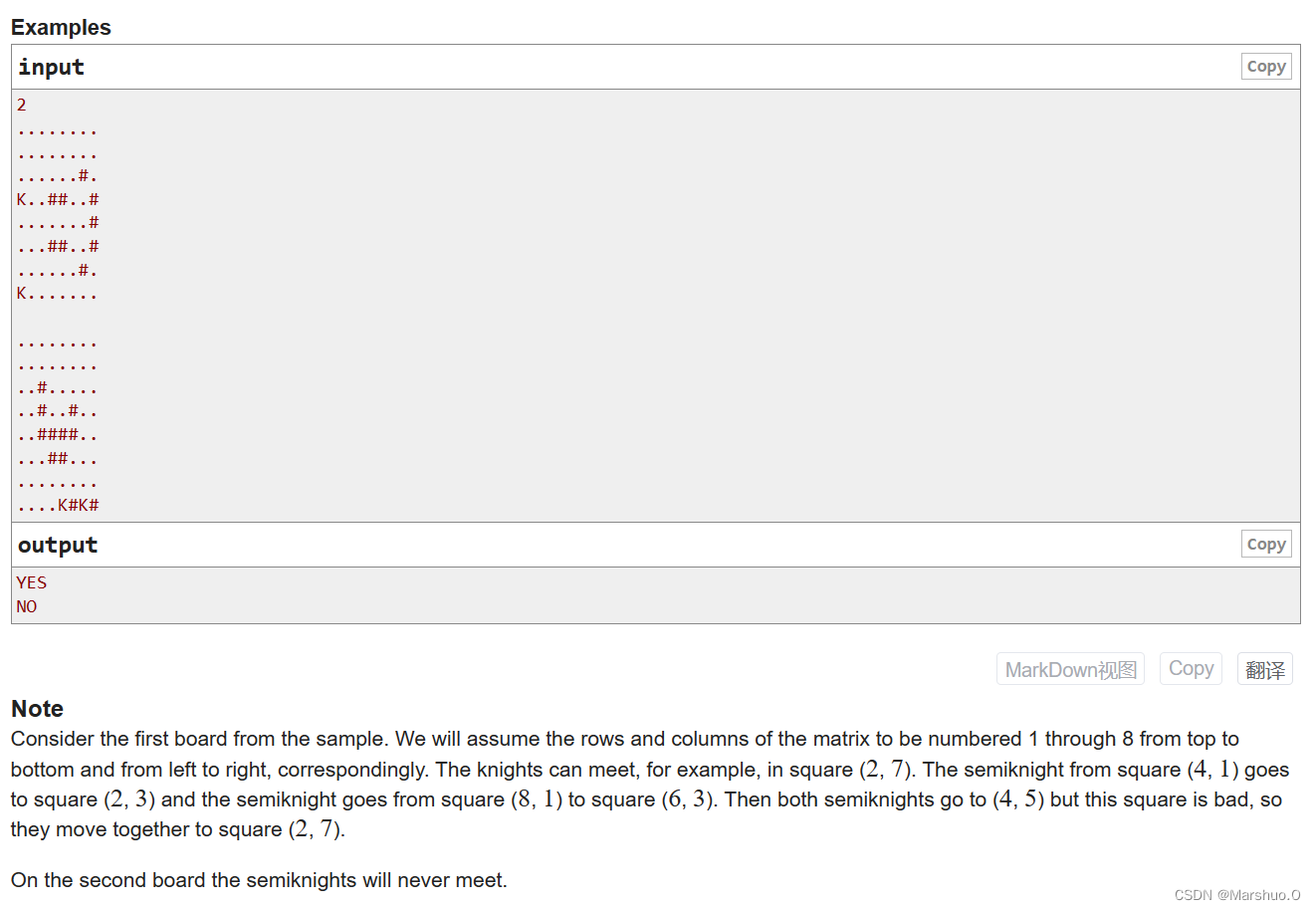
A. Two Semiknights Meet
题目描述 可知走法为中国象棋中的象的走法 解题思路 利用结构体来存储两个 K K K的位置 x , y x,y x,y,因为两个 K K K同时走,所以会出现两种情况 相向而行,两者距离减少 相反而行,两者距离不变 我们完全可以不考虑格子是好…...

〔011〕Stable Diffusion 之 解决绘制多人或面部很小的人物时面部崩坏问题 篇
✨ 目录 🎈 脸部崩坏🎈 下载脸部修复插件🎈 启用脸部修复插件🎈 插件生成效果🎈 插件功能详解🎈 脸部崩坏 相信很多人在画图时候,特别是画 有多个人物 图片或者 人物在图片中很小 的时候,都会很容易出现面部崩坏的问题这是由于神经网络无法完全捕捉人脸的微妙细节…...
在ubuntu+cpolar+rabbitMQ环境下,实现mq服务端远程访问
文章目录 前言1.安装erlang 语言2.安装rabbitMQ3. 内网穿透3.1 安装cpolar内网穿透(支持一键自动安装脚本)3.2 创建HTTP隧道 4. 公网远程连接5.固定公网TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 RabbitMQ是一个在 AMQP(高级消息队列协议)基…...

Vue elementui 实现表格selection的默认勾选,翻页记录勾选状态
需求:当弹出一个列表页数据,对其进行筛选选择。 列表更新,填充已选数据 主要使用toggleRowSelection 代码如下: <el-table v-loading"loading" :data"drugList" selection-change"handleSelection…...

CloudCompare——统计滤波
目录 1.统计滤波2.软件实现3.完整操作4.算法源码5.相关代码 本文由CSDN点云侠原创,CloudCompare——统计滤波,爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 1.统计滤波 算法原理见:PCL 统计滤波器…...
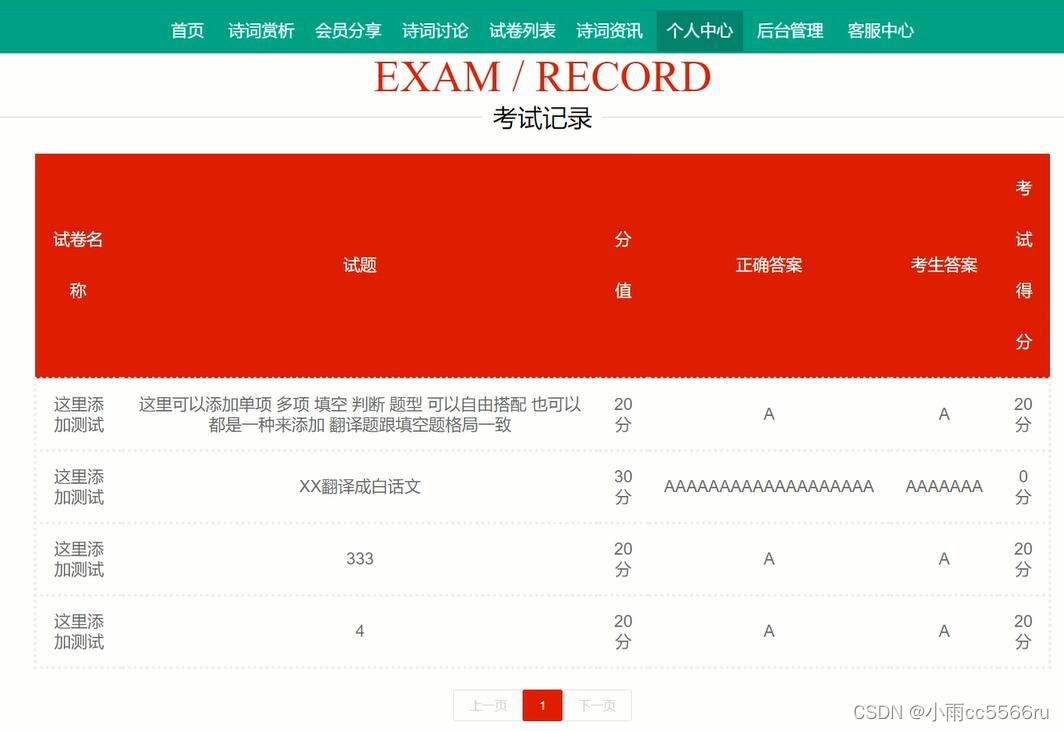
nodejs+vue古诗词在线测试管理系统
一开始,本文就对系统内谈到的基本知识,从整体上进行了描述,并在此基础上进行了系统分析。为了能够使本系统较好、较为完善的被设计实现出来,就必须先进行分析调查。基于之前相关的基础,在功能上,对新系统进…...

174-地下城游戏
题目 恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。 骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻…...

Linux定时任务crontab
常用命令 crontab -e 进入定时脚本,编辑后保存即立即生效 crontab -l 查看用户定时脚本 tail -f /var/log/cron 查看执行日志 service crond status 查看定时器运行状态 service crond restart 重启定时器 定时任务不执行原因 定时任务设置的格式正确,手…...

golang字符串切片去重
函数的功能是从输入的字符串切片中去除重复的元素,并返回去重后的结果。具体的实现逻辑如下: 创建一个空的结果切片result,用于存储去重后的字符串。创建一个临时的maptempMap,用于存放不重复的字符串。map的键是字符串࿰…...

git如何检查和修改忽略文件和忽略规则
查询忽略规则 使用命令行:git status --ignored,进行查询, 例: $ git status --ignored On branch develop Your branch is up to date with origin/develop.Ignored files:(use "git add -f <file>..." to inc…...

Android AppCompatActivity标题栏操作
使用 AndroidStudio 新建的工程默认用 AppCompatActivity ,是带标题栏的。 记录下 修改标题栏名称 和 隐藏标题栏 的方法。 修改标题栏名称 Override protected void onCreate(Bundle savedInstanceState) {super.onCreate(savedInstanceState);setContentView(R…...

解决conda activate报错
解决方法 source ~/anaconda3/bin/activate或 source ~/miniconda3/bin/activate然后就可以使用 conda activate xxx环境了 问题解析 请参考github:https://github.com/conda/conda/issues/7980...
)
FreeMarker--表达式和运算符的用法(全面/有示例)
原文网址:FreeMarker--表达式和运算符的用法(全面/有示例)_IT利刃出鞘的博客-CSDN博客 简介 本文介绍FreeMarker的表达式和运算符的用法。 表达式是FreeMarker的核心功能。表达式放置在插值语法(${...})之中时,表明需要输出表达…...
)
设计模式 -- 策略模式(传统面向对象与JavaScript 的对比实现)
设计模式 – 策略模式(传统面向对象与JavaScript 的对比实现) 文章目录 设计模式 -- 策略模式(传统面向对象与JavaScript 的对比实现)使用策略模式计算年终奖初级实现缺点 使用组合函数重构代码缺点 使用策略模式重构代码传统的面…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...
