法线矩阵推导
法线矩阵推导
https://zhuanlan.zhihu.com/p/72734738
https://juejin.cn/post/7113952418613690382
https://blog.csdn.net/wangjianxin97?type=blog
1、为什么需要法线矩阵
vec3 normalEyeSpace = modelViewMatrix * normal;
如果模型矩阵执行了非等比缩放, 顶点的改变会导致法向量不再保持垂直关系。
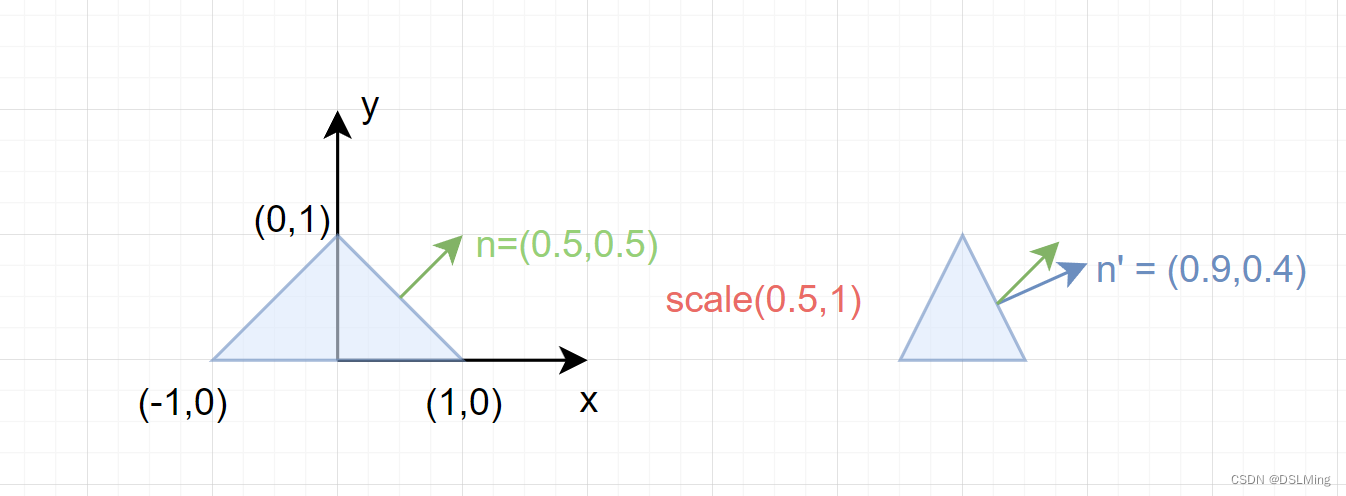
缩放后 n n n不在与线段垂直了, 真正垂直的是 n ′ n' n′。
three.js 代码:
const geometry = new THREE.BufferGeometry()
const position = [];
const normals = [];
position.push(-1, 0, 0)
position.push(1, 0, 0)
position.push(0, 1, 0)normals.push(0.5, 0.5, 0)
normals.push(0.5, 0.5, 0)
normals.push(0.5, 0.5, 0)geometry.setAttribute('position', new THREE.Float32BufferAttribute(position, 3))
geometry.setAttribute('normal', new THREE.Float32BufferAttribute(normals, 3))const material = new THREE.ShaderMaterial({vertexShader: `varying vec3 vNormal;void main() {vec4 mvPosition = modelViewMatrix * vec4( position, 1.0 );gl_Position = projectionMatrix * mvPosition;vNormal = normal;}`,fragmentShader: `varying vec3 vNormal;uniform mat3 normalMatrix;void main() {gl_FragColor = vec4( vNormal, 1.0 );}`,
});const mesh = new THREE.Mesh(geometry, material);
mesh.scale.set(0.5, 1, 1)
2 法向量矩阵推导
约定:
- 向量用小写字母的表示
- 转换矩阵用大写字母表示
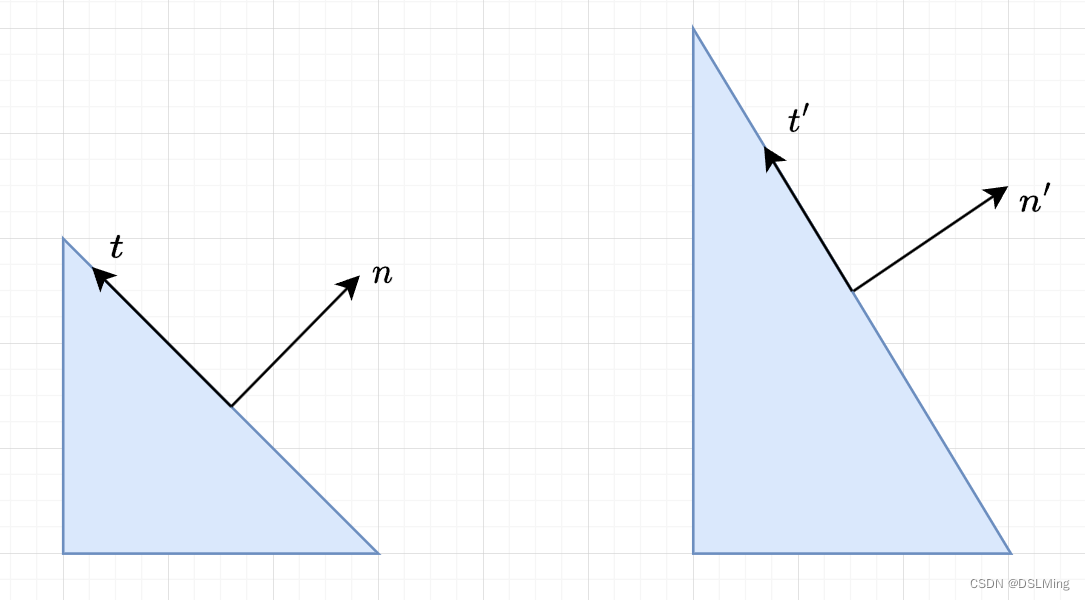
假设矩阵 G G G 转换法向量, 矩阵 M M M转换切线。
如果转换到视图空间,那么 M M M就是modelViewMatrix, 如果转换到世界空间, M M M就是modelMatrix。
根据假设有:
n ′ = G n t ′ = M t n' = G n \\ t' = M t \\ n′=Gnt′=Mt
根据几何关系有:
n ⋅ t = n ′ ⋅ t ′ = 0 n \cdot t = n' \cdot t' = 0 n⋅t=n′⋅t′=0
带入有:
n ′ ⋅ t ′ = ( G n ) ⋅ ( M t ) = ( G n ) T ( M t ) = n T G T M t \begin{aligned} n' \cdot t' &= (G n) \cdot (M t) \\ &= (G n)^{T} (M t) \\ &= n^{T} G^{T} M t \\ \end{aligned} n′⋅t′=(Gn)⋅(Mt)=(Gn)T(Mt)=nTGTMt
因为(向量点积用矩阵表示):
n ⋅ t = n T t = n ′ ⋅ t ′ n \cdot t = n^{T} t = n' \cdot t' n⋅t=nTt=n′⋅t′
所以,满足上式, 只需:
G T M = I G^{T} M = I GTM=I
因此:
G T = M − 1 ( G T ) T = ( M − 1 ) T G = ( M − 1 ) T \begin{aligned} G^{T} &= M^{-1} \\ (G^{T})^{T} &= (M^{-1})^{T} \\ G &= (M^{-1})^{T} \end{aligned} GT(GT)TG=M−1=(M−1)T=(M−1)T
相关文章:

法线矩阵推导
法线矩阵推导 https://zhuanlan.zhihu.com/p/72734738 https://juejin.cn/post/7113952418613690382 https://blog.csdn.net/wangjianxin97?typeblog 1、为什么需要法线矩阵 vec3 normalEyeSpace modelViewMatrix * normal;如果模型矩阵执行了非等比缩放, 顶点的改变会导致法…...
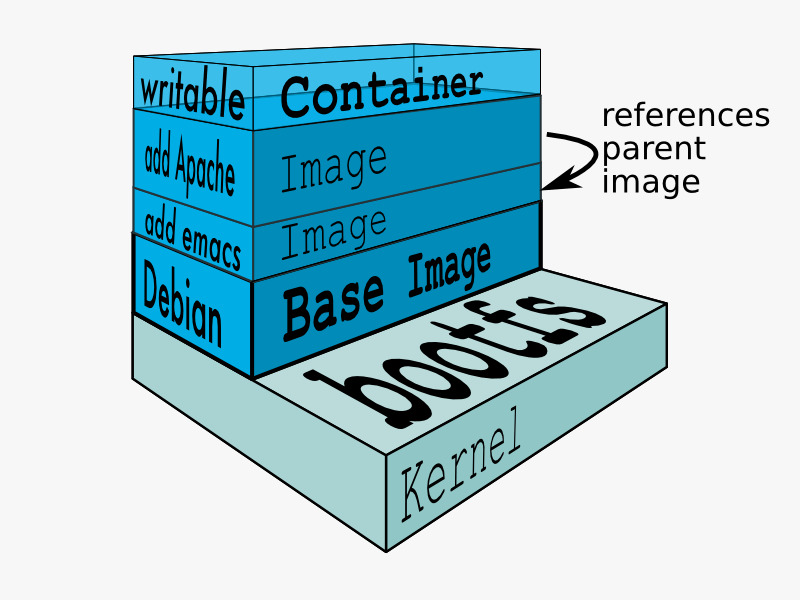
对容器、虚拟机和 Docker 的初学者友好介绍
一、说明 如果你是一个程序员或技术人员,你可能至少听说过Docker:一个有用的工具,用于在“容器”中打包,运输和运行应用程序。很难不这样做,这些天它得到了所有的关注 - 来自开发人员和系统管理员。即使是像谷歌、VMwa…...

linux部署clickhouse(单机)
一、下载安装 1.1、下载地址 阿里巴巴开源镜像站-OPSX镜像站-阿里云开发者社区阿里巴巴开源镜像站,免费提供Linux镜像下载服务,拥有Ubuntu、CentOS、Deepin、MongoDB、Apache、Maven、Composer等多种开源软件镜像源,此外还提供域名解析DNS、…...

vue组件注册
组件注册分为全局注册和局部注册 全局注册 在 main.js 或者入口文件中 import { createApp } from vue; import MyComponent from ./components/MyComponent.vue;const app createApp();app.component(my-component, MyComponent);app.mount(#app); 我们首先通过createApp…...
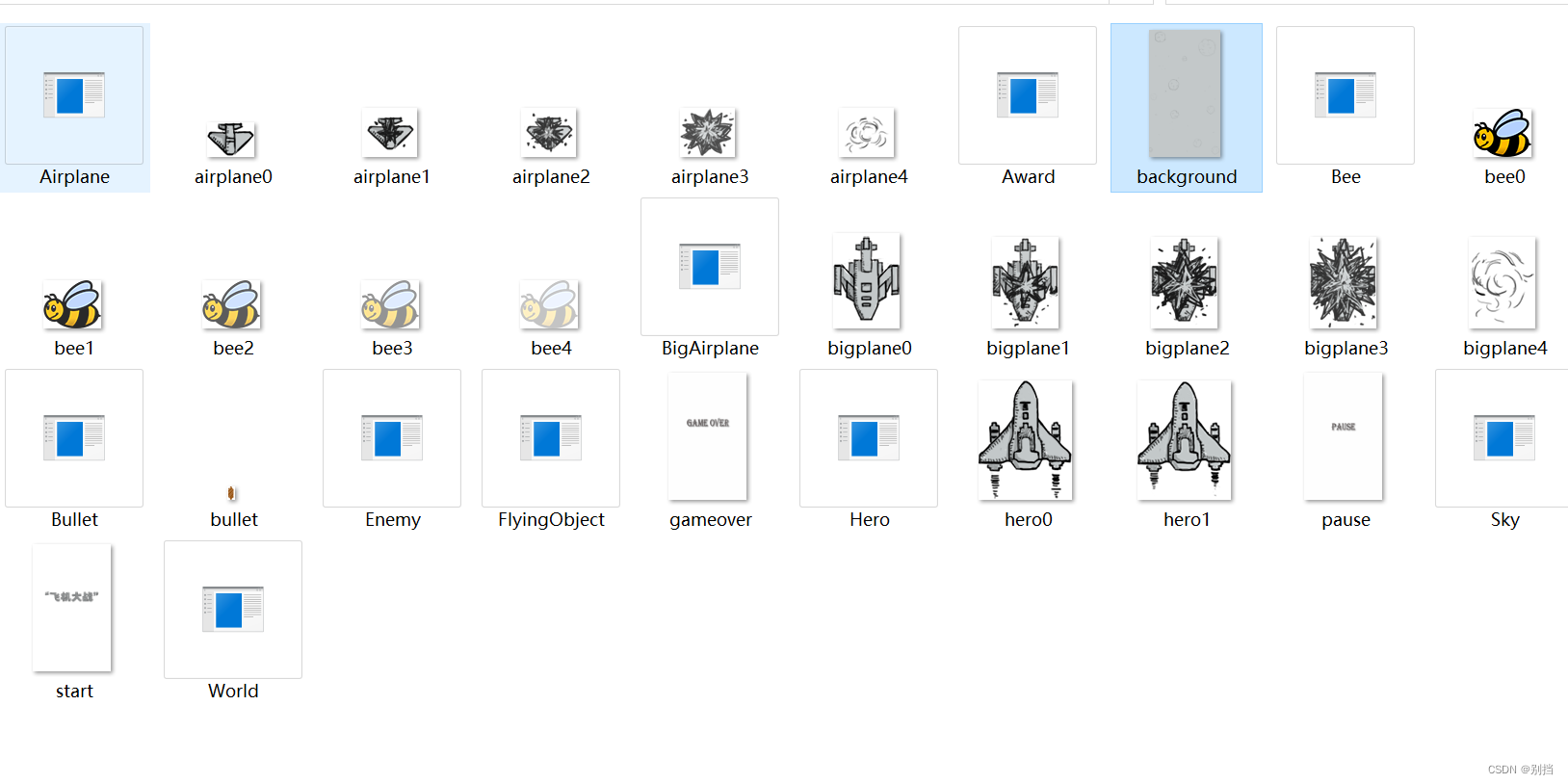
day20 飞机大战射击游戏
有飞行物类 飞行 爆炸 的连环画, 飞行的背景图 , 子弹图, 还有游戏开始 暂停 结束 的画面图。 设计一个飞机大战的小游戏, 玩家用鼠标操作hero飞行机, 射出子弹杀死敌机,小蜜蜂。 敌机可以获得分数&…...
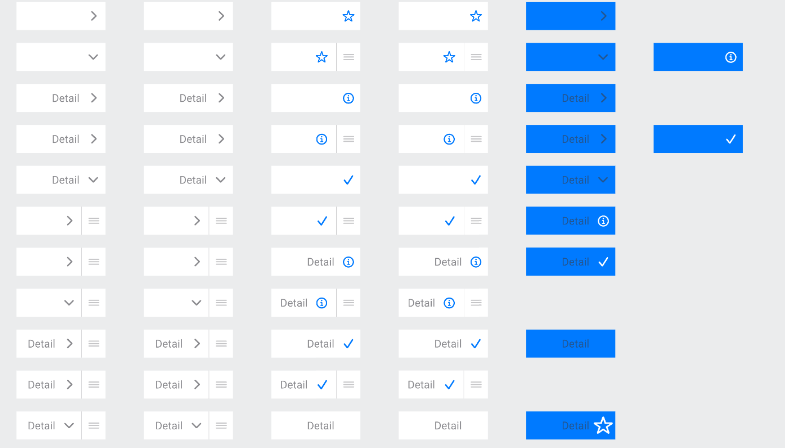
iOS设计规范是什么?都有哪些具体规范
iOS设计规范是苹果为移动设备操作系统iOS制定的设计指南。iOS设计规范的制定保证了苹果应用在外观和操作上的一致性和可用性,从而提高了苹果界面设计的用户体验和应用程序的成功性。本文将从七个方面全面分析iOS设计规范。 1.iOS设计规范完整版分享 由「即时设计」…...

动手学深度学习-pytorch版本(二):线性神经网络
参考引用 动手学深度学习 1. 线性神经网络 神经网络的整个训练过程,包括: 定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型。经典统计学习技术中的线性回归和 softmax 回归可以视为线性神经网络 1.1 线性回归 回归 (regression) 是能为一个或多个…...
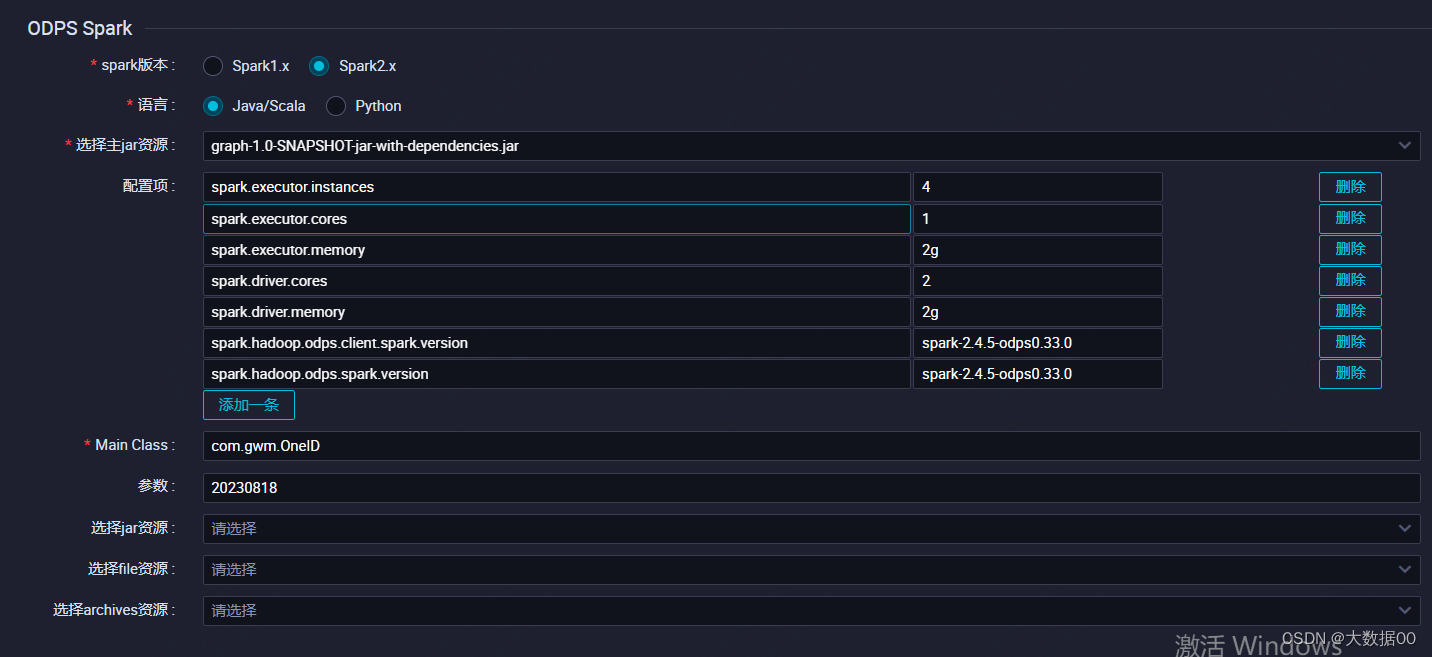
Spark 图计算ONEID 进阶版
0、环境信息 本文采用阿里云maxcompute的spark环境为基础进行的,搭建本地spark环境参考搭建Windows开发环境_云原生大数据计算服务 MaxCompute-阿里云帮助中心 版本spark 2.4.5,maven版本大于3.8.4 ①配置pom依赖 详见2-1 ②添加运行jar包 ③添加配置信…...

Comparable和Comparator区别
Comparable和Comparator接口都是实现集合中元素的比较、排序的,众所周知,诸如Integer,double等基本数据类型,java可以对他们进行比较,而对于类的比较,需要人工定义比较用到的字段比较逻辑。总体来讲&#x…...

JAVA知识点梳理
我的博客:lcatake_flume,spark,zookeeper-CSDN博客 看不懂的话进去看看 1.Java的三个版本 JAVASE 基本 JAVAME 微缩 JAVAEE 标准 3.java的特点 面向对象 跨平台:jvm将java文件转变为字节码文件(.class)在多个系统中运 行字…...
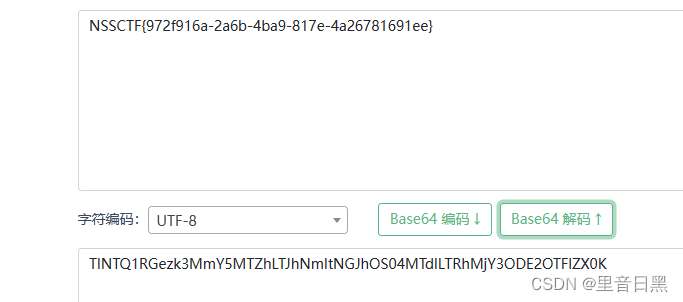
[SWPUCTF 2022 新生赛]ez_ez_php
这段代码是一个简单的PHP文件处理脚本。让我们逐行进行分析: error_reporting(0); - 这行代码设置了错误报告的级别为0,意味着不显示任何错误。 if (isset($_GET[file])) { - 这行代码检查是否存在一个名为"file"的GET参数。 if ( substr($_…...
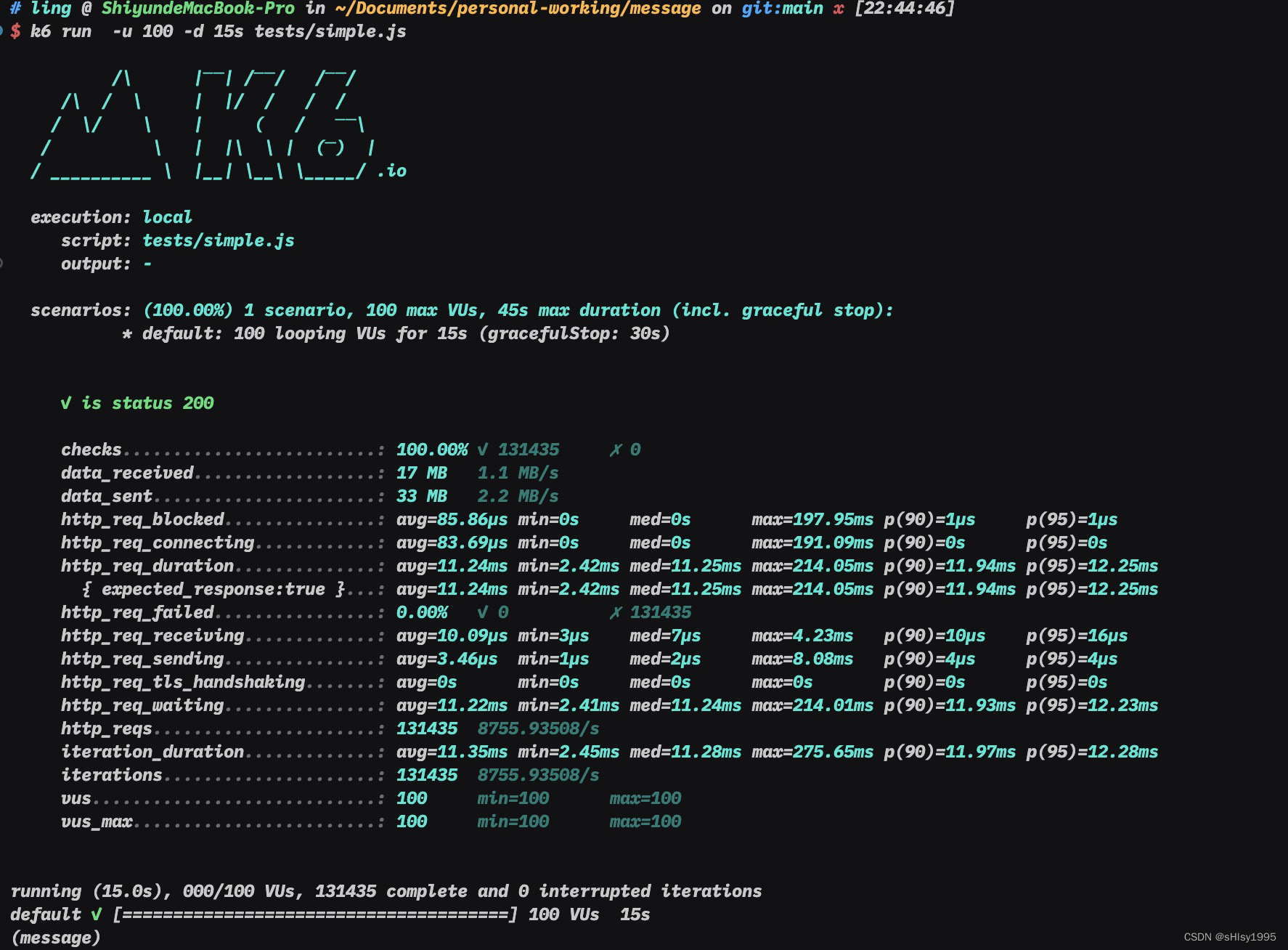
GraphQL strawberry的使用回顾和体会
GraphQL vs RESTful 简单来说GraphQL 比起 RESTful 集成额外一些功能 出入参校验、序列化 (简化后端编程)自由可选的返回数据字段 (简化一些多余接口开发和沟通联调成本) 这些都是优点了。 开发效率在项目初期是很重要的,需要快速原型化。 但是后期稳定后&#…...

08无监督学习——聚类
1.什么是聚类任务? 类别:无监督学习 目的:通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。 1.1K均值聚类 步骤: 随机选取样本作为初始均值向量(初始值:k的值【即几个簇】)分别…...

Python使用OpenCV库对彩色图像进行通道分离
目录 1、解释说明: 2、使用示例: 3、注意事项: 1、解释说明: 在Python中,我们可以使用OpenCV库对彩色图像进行通道分离。通道分离是将彩色图像的每个像素分解为三个通道(红、绿、蓝)的过程。…...

前端面试:【CSS】盒模型、选择器、布局、响应式设计、Flexbox 与 Grid
CSS(层叠样式表)是用于控制网页外观和布局的重要语言。在这篇文章中,我们将深入探讨CSS的基础知识,包括盒模型、选择器、布局、响应式设计,以及弹性盒子(Flexbox)和网格布局(Grid&am…...

深入浅出通过PHP封装根据商品ID获取抖音商品详情数据方法
抖音商城商品详情数据是指商品在抖音商城中的展示信息,包括商品的标题、描述、价格、图片等。商家可以通过商品详情数据了解用户对商品的兴趣和需求,从而进行优化和调整。 商品详情数据还可以帮助商家评估商品的销售情况和市场竞争力,为制定…...
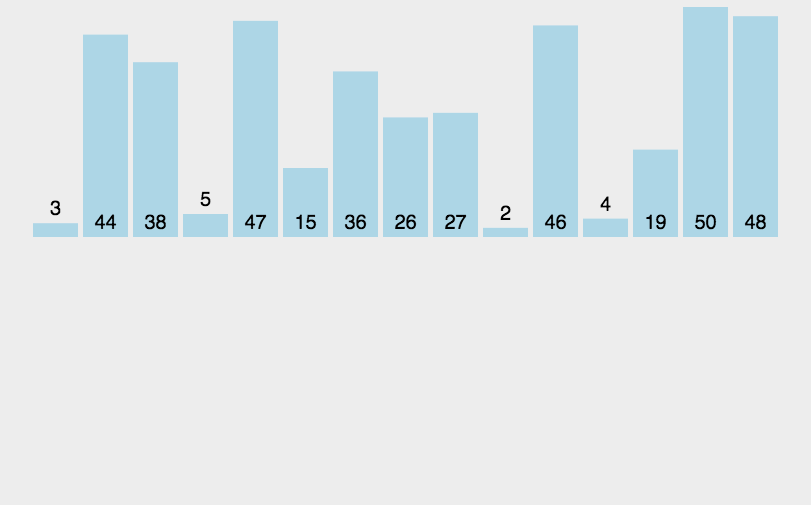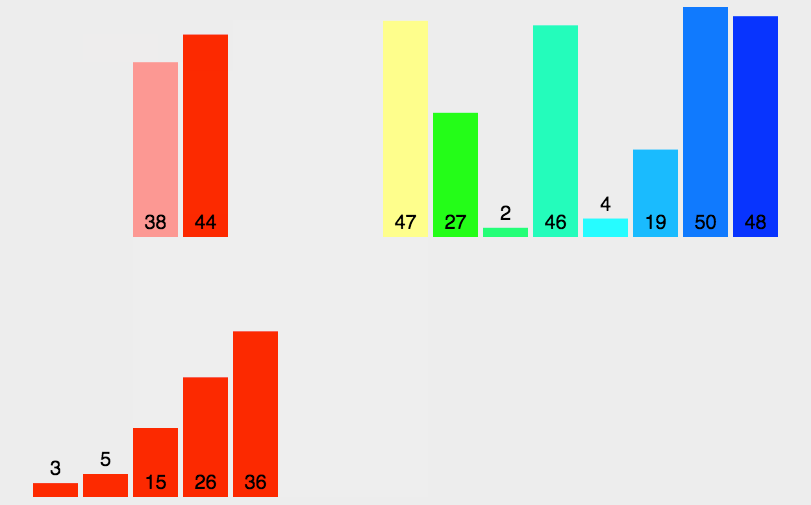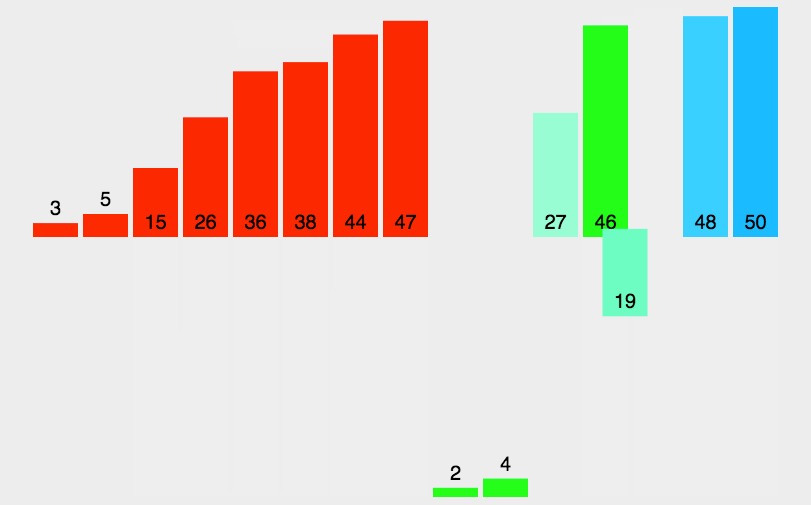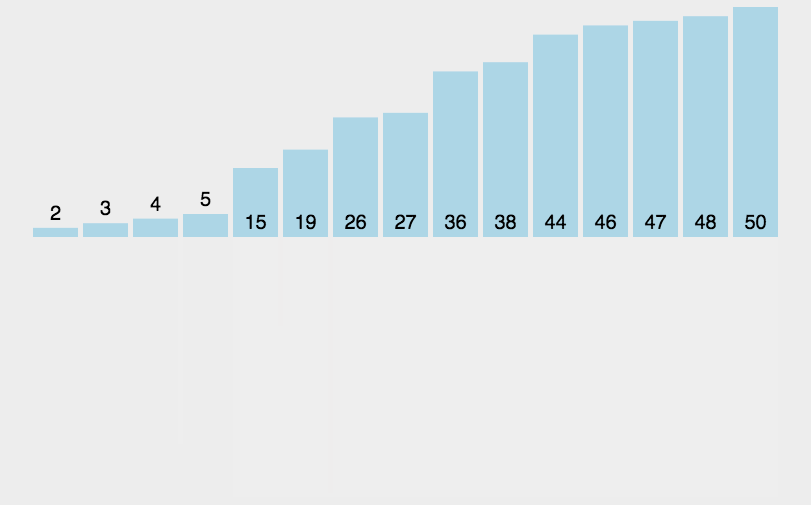
排序(七种排序)
1.插入排序 2.希尔排序 3.选择排序 4.堆排序 5.冒泡排序 6.快速排序 7.归并排序 1.插入排序 1.1思路 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 1.2实现 //插入排…...
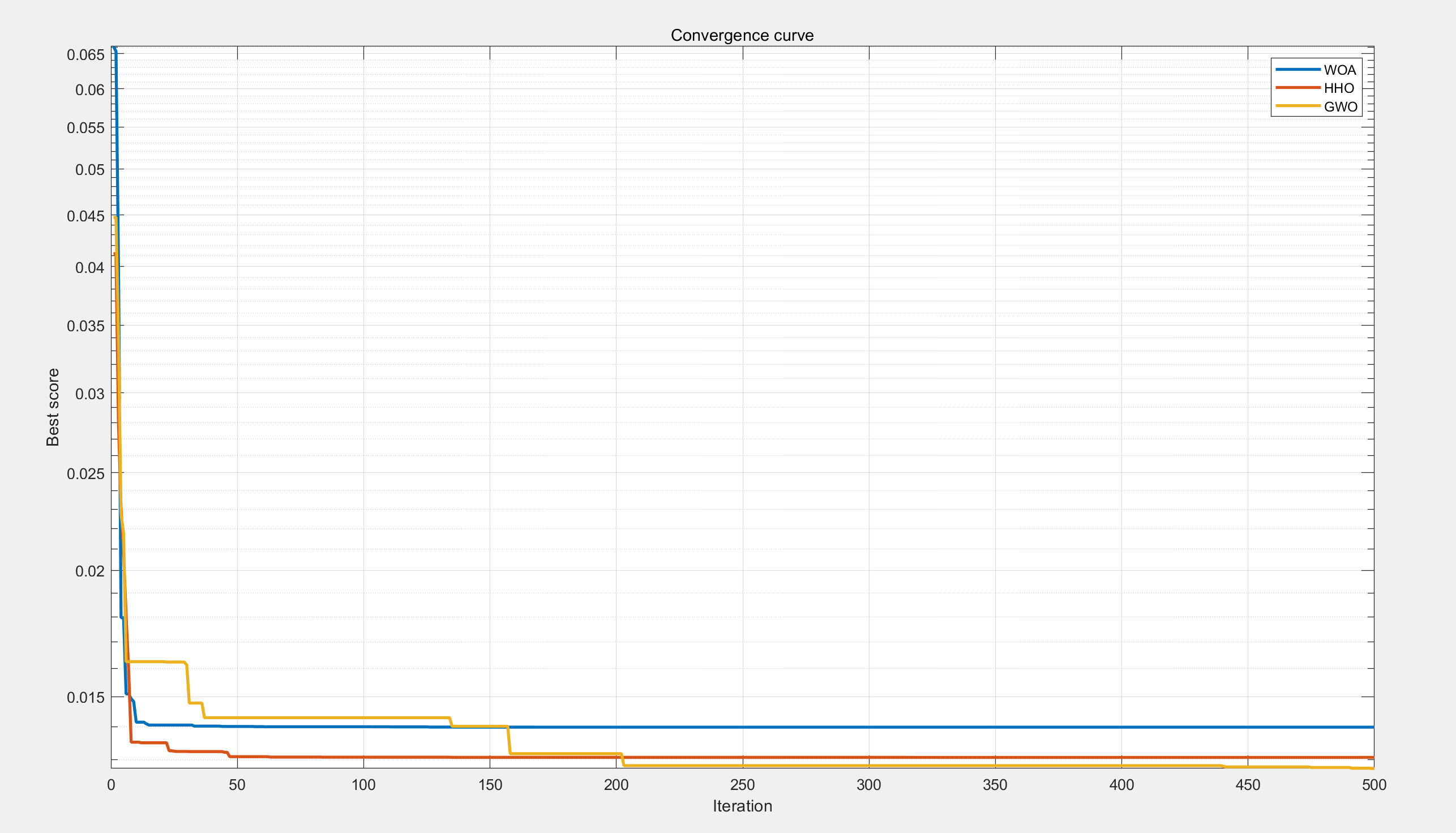
【工程优化问题】基于鲸鱼、萤火虫、灰狼优化算法的张力、压缩弹簧设计问题研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

sap ui5刷新页面的方式
1.第一种 window.location.reload();2.第二种 如果你想在UI5应用程序中使用MVC模式来处理页面刷新,可以通过重新加载当前路由来实现刷新。首先,确保你有一个Router对象实例: var oRouter = sap.ui.core.UIComponent.getRouterFor(this);然后&...

Java课题笔记~ Fastjson 概述
3.3 JSON串和Java对象的相互转换 学习完 json 后,接下来聊聊 json 的作用。 以后我们会以 json 格式的数据进行前后端交互。前端发送请求时,如果是复杂的数据就会以 json 提交给后端;而后端如果需要响应一些复杂的数据时,也需要…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...
