08无监督学习——聚类
1.什么是聚类任务?
类别:无监督学习
目的:通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。
1.1K均值聚类
步骤:
- 随机选取样本作为初始均值向量(初始值:k的值【即几个簇】)
- 分别计算每个样本点到初始均值向量的距离,距离哪个点最近就属于哪个簇
- 每个簇重新计算中心点,重复第二步直到收敛
距离计算:
距离度量/非距离度量:若它是一个距离度量则应该满足以下性质:
- 非负性:dist(x,y)>=0
- 同一性:dist(x,y)=0,当且仅当x=y
- 对称性:dist(x,y) = dist(y,x)
- 直递性:dist(x,z) <= dist(x,y)+dist(y,z)
1.1.1 曼哈顿距离
d i s t m a n ( x i , x j ) = ∥ x i − x j ∥ 1 = ∑ μ = 1 n ∣ x i μ − x j μ ∣ {\rm{dis}}{{\rm{t}}_{man}}({x_i},{x_j}) = {\left\| {{x_i} - {x_j}} \right\|_1} = \sum\limits_{\mu = 1}^n {\left| {{x_{i\mu }} - {x_{j\mu }}} \right|} distman(xi,xj)=∥xi−xj∥1=μ=1∑n∣xiμ−xjμ∣
1.1.2欧氏距离
dist e d ( x i , x j ) = ∥ x i − x j ∥ 2 = ∑ u = 1 n ∣ x i u − x j u ∣ 2 \operatorname{dist}_{\mathrm{ed}}\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=\left\|\boldsymbol{x}_i-\boldsymbol{x}_j\right\|_2=\sqrt{\sum_{u=1}^n\left|x_{i u}-x_{j u}\right|^2} disted(xi,xj)=∥xi−xj∥2=u=1∑n∣xiu−xju∣2
1.1.3 切比雪夫距离
切比雪夫距离定义为两个向量在任意坐标维度上的最大差值。换句话说,它就是沿着一个轴的最大距离。切比雪夫距离通常被称为棋盘距离,因为国际象棋的国王从一个方格到另一个方格的最小步数等于切比雪夫距离。
D ( x , y ) = max i ( ∣ x i − y i ∣ ) D(x,y) = \mathop {\max }\limits_i (|{x_i} - {y_i}|) D(x,y)=imax(∣xi−yi∣)
切比雪夫距离通常用于特定的用例,这使得它很难像欧氏距离或余弦相似度那样作为通用的距离度量。因此,在确定适合用例时才使用它。
1.1.4 闵式距离
给定样本 x i = ( x i 1 ; x i 2 ; … ; x i n ) {x_i} = ({x_{i1}};{x_{i2}}; \ldots ;{x_{in}}) xi=(xi1;xi2;…;xin)与 x j = ( x j 1 ; x j 2 ; … ; x j n ) {x_j} = ({x_{j1}};{x_{j2}}; \ldots ;{x_{jn}}) xj=(xj1;xj2;…;xjn),最常用的就是闵可夫斯基距离。
d i s t m k ( x i , x j ) = ( ∑ u = 1 n ∣ x i u − x j u ∣ p ) 1 p dis{t_{mk}}({x_i},{x_j}) = {(\sum\limits_{u = 1}^n {{{\left| {{x_{iu}} - {x_{ju}}} \right|}^p}} )^{{1 \over p}}} distmk(xi,xj)=(u=1∑n∣xiu−xju∣p)p1
- p=1时,闵可夫斯基距离即为曼哈顿距离( Manhattan distance )
- p=2时,闵可夫斯基距离即为欧式距离( Euclidean distance )
- p= ∞ \infty ∞时,闵可夫斯基距离即为切比雪夫距离(Chebyshev Distance )
1.1.5 余弦相似度(Cosine Similarity )
余弦相似度经常被用作抵消高维欧式距离问题。余弦相似度是指两个向量夹角的余弦。
两个方向完全相同的向量的余弦相似度为1,而两个彼此相对的向量的余弦相似度为- 1。注意,它们的大小并不重要,因为这是在方向上的度量。
D ( x , y ) = cos ( θ ) = x ⋅ y ∥ x ∥ ∥ y ∥ D(x,y) = \cos (\theta ) = {{x \cdot y} \over {\left\| x \right\|\left\| y \right\|}} D(x,y)=cos(θ)=∥x∥∥y∥x⋅y
用例:当我们对高维数据向量的大小不关注时,可以使用余弦相似度。列如,对于文本分析,当数据以单词计数表示时,经常使用此度量。例如,当一个单词在一个文档中比另一个单词更频繁出现时,这并不一定意味着文档与该单词更相关。可能是文件长度不均匀或者计数的重要性不太重要。我们最好使用忽略幅度的余弦相似度。
1.1.6 汉明距离(Hamming Distance )
汉明距离是两个向量之间不同值的个数。它通常用于比较两个相同长度的二进制字符串。它还可以用于字符串,通过计算不同字符的数量来比较它们之间的相似程度。
缺点:当两个向量长度不相等时,汉明距离使用起来很麻烦。
用例∶典型的用例包括数据通过计算机网络传输时的错误纠正/检测。它可以用来确定二进制字中失真的数目,作为估计误差的一种方法。此外,你还可以使用汉明距离来度量分类变量之间的距离。
1.2密度聚类(Density-based Spatial Clusteringof Applications with Noise )
基于密度的聚类,此类算法假设聚类结构能通过样本分布的紧密程度确定
密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果
- 层次聚类
- 高斯混合模型聚类
- 聚类效果的衡量指标
1.3层次聚类(hierarchicalclustering)
试图在不同层次对数据集进行划分,从而形成树形的聚类结构.数据集的划分可采用"自底向上"的聚合策略,也可采用"自顶向下"的拆分策略.
AGNES是一种采用自底向上聚合策略的层次聚类算法.它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数。
AGNES算法步骤:
( 1)初始化,每个样本当做一个簇
( 2)计算任意两簇距离,找出距离最近的两个簇,合并这两簇
(3)重复步骤2…
直到,最远两簇距离超过阈值,或者簇的个数达到指定值,终止算法
DIANA算法步骤:
( 1)初始化,所有样本集中归为一个簇
( 2)在同一个簇中,计算任意两个样本之间的距离,找到距离最远的两个样本点a,b,
将a,b作为两个簇的中心;
( 3)计算原来簇中剩余样本点距离a , b 的距离,距离哪个中心近,分配到哪个簇中
( 4)重复步骤2、3…
直到,最远两簇距离不足阈值,或者簇的个数达到指定值,终止算法
层次聚类(Hierarchical Clustering )在生物信息学中的应用
层次聚类是一种比较实用的聚类方法,应用于不同领域的数据分析算法中。
在生物医学信息学领域,层次聚类方法常常用于蛋白质序列数据聚类和基因表达数据的聚类。结构相似的蛋白质,功能也相似,通过聚类将相似功能的蛋白质聚为一类,为研究蛋白质的功能提供帮助。基因表达数据聚类就是将具有相似表达谱的基因聚为一类,称为共表达基因,根据基因的共表达现象推断这些基因的生物学功能,从而对新的基因功能进行注释,对基因的生物学功能研究具有重要意义。
1.4 高斯混合聚类模型
已知样本集D= D = { x 1 , x 2 , . . . , x m } D = \{ {x_1},{x_2},...,{x_m}\} D={x1,x2,...,xm},要将这些样本聚成k类,我们认为样本服从混合高斯分布:
p M ( x ) = ∑ i = 1 k α i ⋅ p ( x ∣ μ i , Σ i ) {p_M}(x) = \sum\limits_{i = 1}^k {{\alpha _i}} \cdot p(x|{\mu _i},{\Sigma _i}) pM(x)=i=1∑kαi⋅p(x∣μi,Σi)
第一步初始化高斯混合分布的模型参数 α i {{\alpha _i}} αi, μ i {\mu _i} μi, Σ i {\Sigma _i} Σi
第二步计算x 由各混合成分生成的后验概率,即观测数据 x j {x_j} xj由第i个分模型生成的概率 p ( z j = i ∣ x j ) p({z_j} = i|{x_j}) p(zj=i∣xj),并记为 γ j i {\gamma _{ji}} γji
γ j i = a i ⋅ p ( x j ∣ μ i , Σ i ) ∑ i = 1 k a i p ( x j ∣ μ i , Σ i ) {\gamma _{ji}} = {{{a_i} \cdot p({x_j}|{\mu _i},{\Sigma _i})} \over {\sum\limits_{i = 1}^k {{a_i}p({x_j}|{\mu _i},{\Sigma _i})} }} γji=i=1∑kaip(xj∣μi,Σi)ai⋅p(xj∣μi,Σi)
第三步计算新的横型参数:
μ i ′ = ∑ j = 1 m γ j i x j ∑ j = 1 m γ j i Σ i ′ = ∑ j = 1 m γ j i ( x j − μ i ′ ) ( x j − μ i ′ ) T ∑ j = 1 m γ j i α i ′ = ∑ j = 1 m γ j i m \begin{aligned} \boldsymbol{\mu}_i^{\prime} & =\frac{\sum_{j=1}^m \gamma_{j i} x_j}{\sum_{j=1}^m \gamma_{j i}} \\ \boldsymbol{\Sigma}_i^{\prime} & =\frac{\sum_{j=1}^m \gamma_{j i}\left(x_j-\mu_i^{\prime}\right)\left(x_j-\mu_i^{\prime}\right)^{\mathrm{T}}}{\sum_{j=1}^m \gamma_{j i}} \\ \alpha_i^{\prime} & =\frac{\sum_{j=1}^m \gamma_{j i}}{m} \end{aligned} μi′Σi′αi′=∑j=1mγji∑j=1mγjixj=∑j=1mγji∑j=1mγji(xj−μi′)(xj−μi′)T=m∑j=1mγji
第四步按照新的模型参数重复2,3步,直到满足停止条件
第五步将每个样本按照入 λ j = arg max i ∈ ( 1 , 2 , . . . , k ) γ j i {\lambda _j} = \mathop {\arg \max }\limits_{i \in (1,2,...,k)} {\gamma _{ji}} λj=i∈(1,2,...,k)argmaxγji, 划入对应的簇。即对每个样本来自哪个分模型的概率大就划入哪个分模型的簇中,最终就得到了k个聚类
总结:
- 分层聚类擅长于发现数据中的嵌入式结构。
- 基于密度的方法在寻找具有相似密度的未知数量的聚类方面表现优异。
- K-means考虑在整个数据集中找到"共识”,K-means考虑数据集中的每个点,并使用该信息在一系列迭代中进化聚类。
- 高斯混合模型考虑重合数据的聚类。
2.性能度量
什么是好的聚类?
目的∶1评估聚类结果的好坏②确立优化的目标
结论︰簇内的样本尺度尽可能彼此相似,簇间的样本尽可能不同。
外部指标∶将聚类结果与某个"参考模型"进行比较,称为"外部指标"”。
a = ∣ S S ∣ , S S = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ = λ j ∗ , i < j ) } , b = ∣ S D ∣ , S D = { ( x i , x j ) ∣ λ i = λ j , λ i ∗ ≠ λ j ∗ , i < j ) } , c = ∣ D S ∣ , D S = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ = λ j ∗ , i < j ) } , d = ∣ D D ∣ , D D = { ( x i , x j ) ∣ λ i ≠ λ j , λ i ∗ ≠ λ j ∗ , i < j ) } , \begin{aligned} & \left.a=|S S|, \quad S S=\left\{\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \mid \lambda_i=\lambda_j, \lambda_i^*=\lambda_j^*, i<j\right)\right\}, \\ & \left.b=|S D|, \quad S D=\left\{\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \mid \lambda_i=\lambda_j, \lambda_i^* \neq \lambda_j^*, i<j\right)\right\}, \\ & \left.c=|D S|, \quad D S=\left\{\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \mid \lambda_i \neq \lambda_j, \lambda_i^*=\lambda_j^*, i<j\right)\right\}, \\ & \left.d=|D D|, \quad D D=\left\{\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) \mid \lambda_i \neq \lambda_j, \lambda_i^* \neq \lambda_j^*, i<j\right)\right\}, \\ & \end{aligned} a=∣SS∣,SS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j)},b=∣SD∣,SD={(xi,xj)∣λi=λj,λi∗=λj∗,i<j)},c=∣DS∣,DS={(xi,xj)∣λi=λj,λi∗=λj∗,i<j)},d=∣DD∣,DD={(xi,xj)∣λi=λj,λi∗=λj∗,i<j)},
相关文章:

08无监督学习——聚类
1.什么是聚类任务? 类别:无监督学习 目的:通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。 1.1K均值聚类 步骤: 随机选取样本作为初始均值向量(初始值:k的值【即几个簇】)分别…...

Python使用OpenCV库对彩色图像进行通道分离
目录 1、解释说明: 2、使用示例: 3、注意事项: 1、解释说明: 在Python中,我们可以使用OpenCV库对彩色图像进行通道分离。通道分离是将彩色图像的每个像素分解为三个通道(红、绿、蓝)的过程。…...

前端面试:【CSS】盒模型、选择器、布局、响应式设计、Flexbox 与 Grid
CSS(层叠样式表)是用于控制网页外观和布局的重要语言。在这篇文章中,我们将深入探讨CSS的基础知识,包括盒模型、选择器、布局、响应式设计,以及弹性盒子(Flexbox)和网格布局(Grid&am…...

深入浅出通过PHP封装根据商品ID获取抖音商品详情数据方法
抖音商城商品详情数据是指商品在抖音商城中的展示信息,包括商品的标题、描述、价格、图片等。商家可以通过商品详情数据了解用户对商品的兴趣和需求,从而进行优化和调整。 商品详情数据还可以帮助商家评估商品的销售情况和市场竞争力,为制定…...
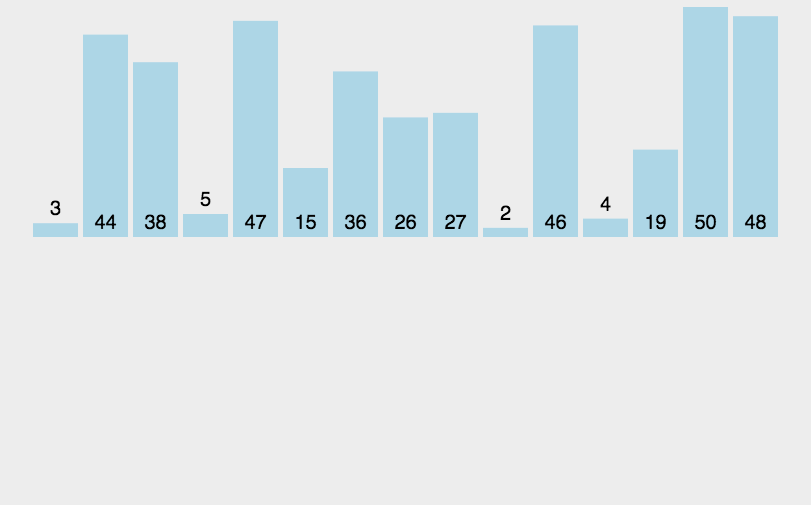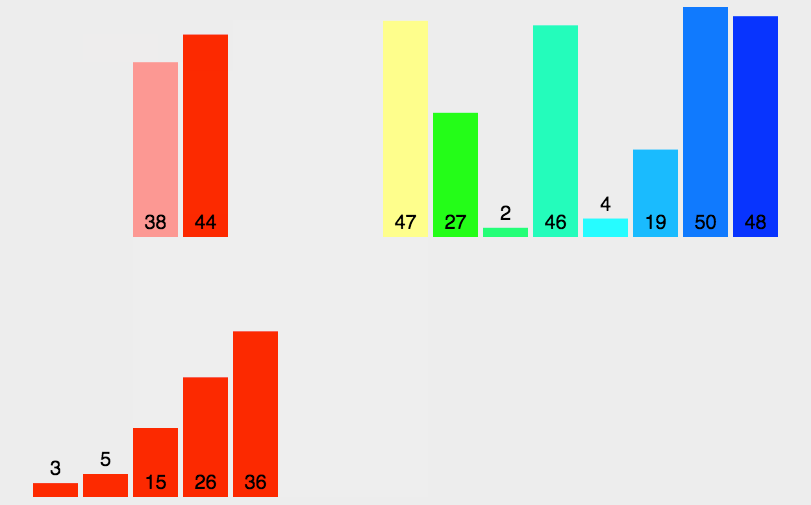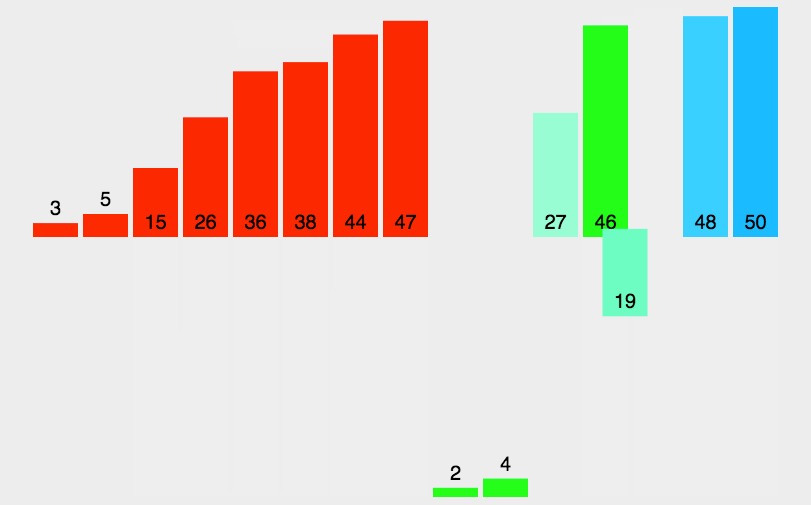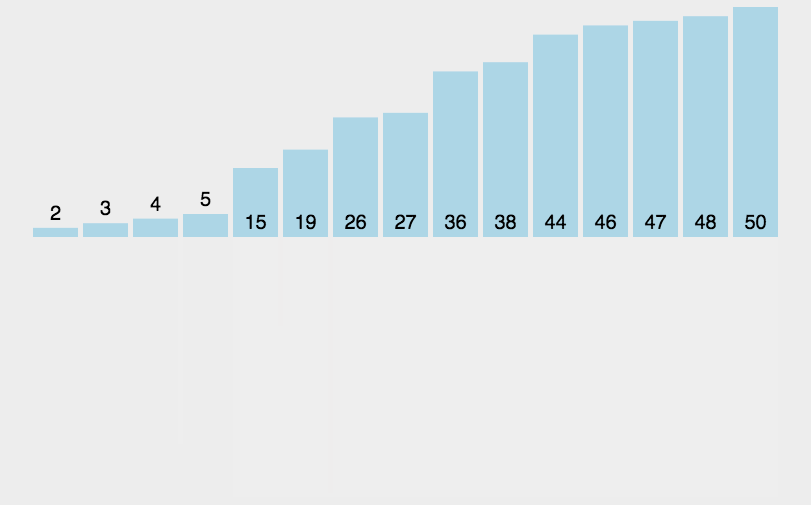
排序(七种排序)
1.插入排序 2.希尔排序 3.选择排序 4.堆排序 5.冒泡排序 6.快速排序 7.归并排序 1.插入排序 1.1思路 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 1.2实现 //插入排…...
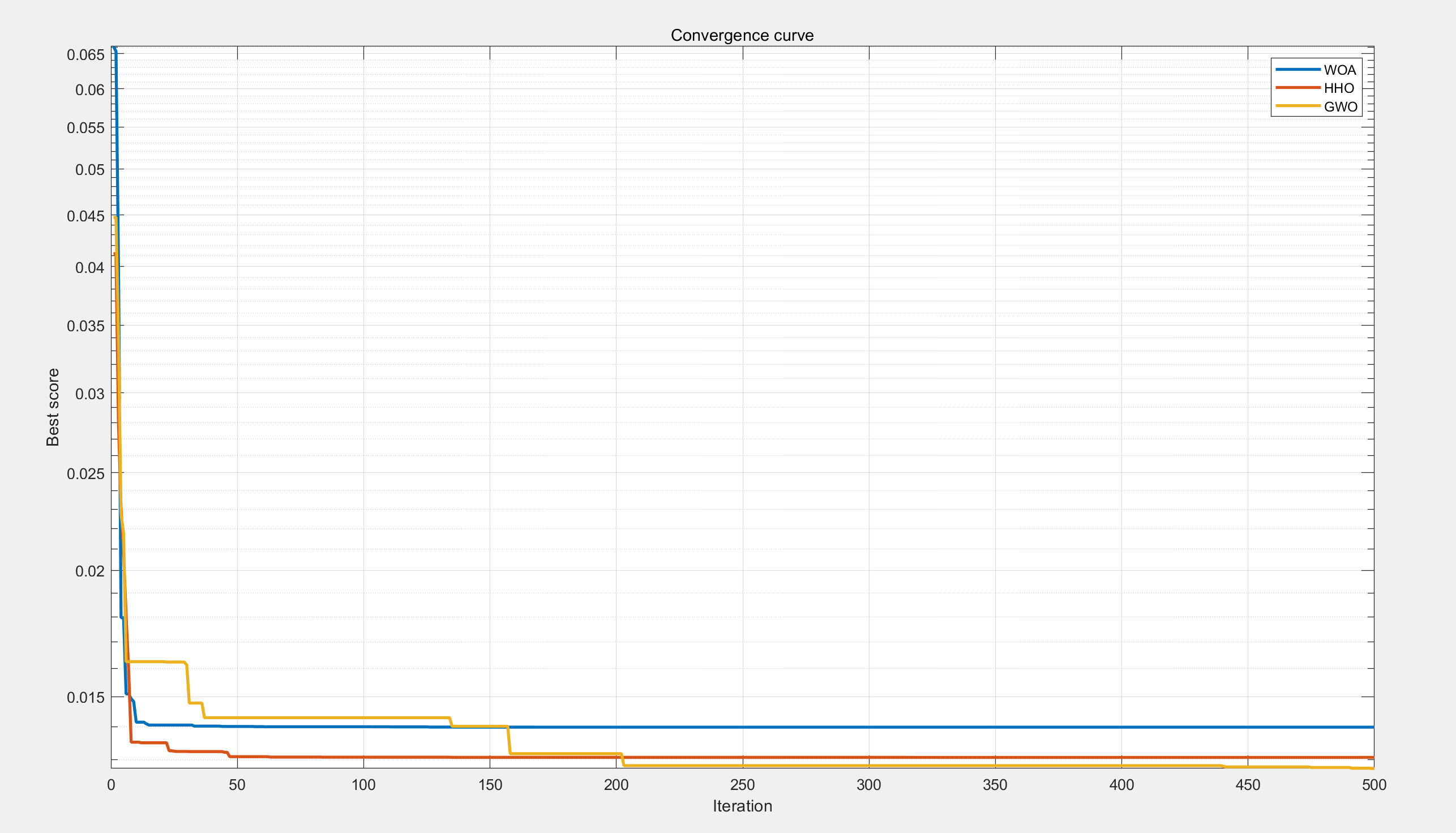
【工程优化问题】基于鲸鱼、萤火虫、灰狼优化算法的张力、压缩弹簧设计问题研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

sap ui5刷新页面的方式
1.第一种 window.location.reload();2.第二种 如果你想在UI5应用程序中使用MVC模式来处理页面刷新,可以通过重新加载当前路由来实现刷新。首先,确保你有一个Router对象实例: var oRouter = sap.ui.core.UIComponent.getRouterFor(this);然后&...

Java课题笔记~ Fastjson 概述
3.3 JSON串和Java对象的相互转换 学习完 json 后,接下来聊聊 json 的作用。 以后我们会以 json 格式的数据进行前后端交互。前端发送请求时,如果是复杂的数据就会以 json 提交给后端;而后端如果需要响应一些复杂的数据时,也需要…...

Arduino 入门学习笔记11 读写内置EEPROM
Arduino 入门学习笔记11 使用I2C读写EEPROM 一、Arduino 内置EEPROM介绍二、EEPROM 操作1. 包含EEPROM库:2. 写入数据到EEPROM:3. 从EEPROM读取数据4. 完整示例: 一、Arduino 内置EEPROM介绍 Arduino的内置EEPROM(Electrically E…...

【Nginx】安装make后遇到/bin/sh: 第 0 行:cd: ../pcre-8.38: 没有那个文件或目录
遇到/bin/sh: 第 0 行:cd: ../pcre-8.38: 没有那个文件或目录 需安装pcre 下载 http://downloads.sourceforge.net/project/pcre/pcre/8.35/pcre-8.35.tar.gz 上传到/usr/local下 pcre解压编译 tar -zxvf pcre-8.35.tar.gz mv pcre-8.35 /usr/local/src/cd /usr/local/src/p…...
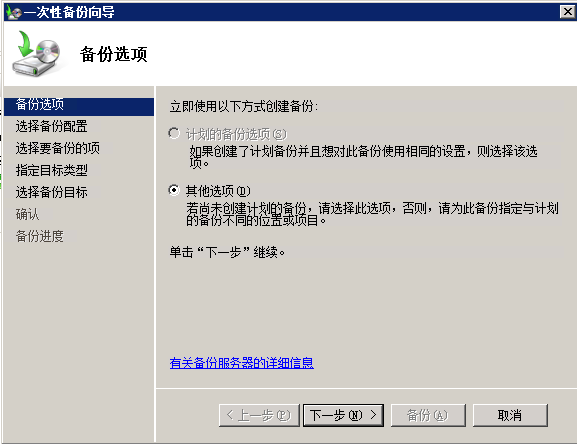
在Windows Server 2008上启用自动文件夹备份
要在Windows Server 2008上启用自动文件夹备份,您可以使用内置的Windows备份功能。下面是如何设置它的方法: 1. 点击“开始”按钮并选择“服务器管理器”,打开“服务器管理器”。 2. 在“服务器管理器”窗口中,单击左侧窗格中的“…...

数据结构—线性表的查找
7.查找 7.1查找的基本概念 问题:在哪里找?——查找表 查找表是由同一类型的数据元素(或记录)构成的集合。由于“集合”中的数据元素之间存在着松散的关系,因此查找表是一种应用灵便的结构。 问题:什么查找&…...
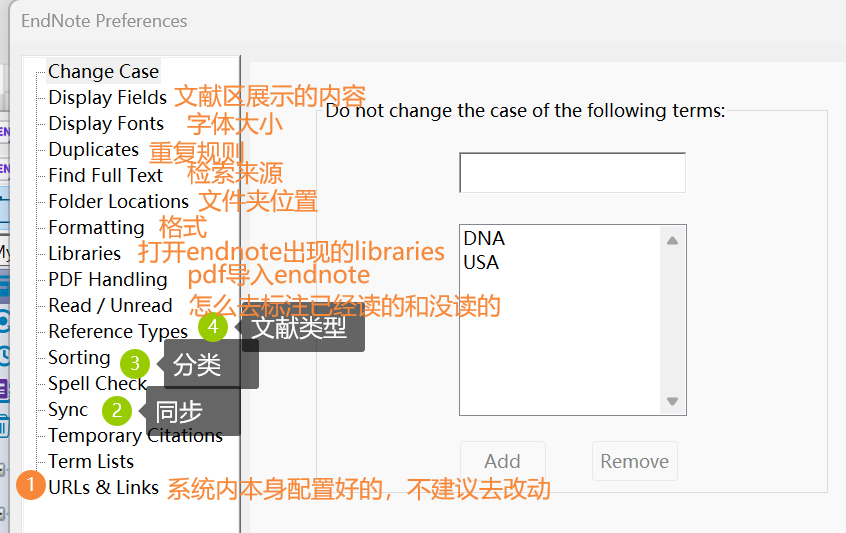
EndNote(一)【界面+功能介绍】
EndNote界面: 顶上小图标的介绍: ①:同步 ②:分享 ③:检索全文 对于第三个(检索全文的功能): (不做任何操作的情况下的界面,检索全文的按钮是灰的&…...

JWT令牌验证
目录 一、JWT介绍 二、安装依赖 三、登陆接口 1、令牌工具类 2、接口代码 四、说明 一、JWT介绍 JWT全称:JSON Web Token (官网:JSON Web Tokens - jwt.io) 定义了一种简洁的、自包含的格式,用于在通信双方以json…...

【微信小程序】下拉刷新功能实现
微信小程序开发系列 文章目录 前言一、onPullDownRefresh函数二、实现1.开启下拉刷新2.监听下拉事件 前言 在开发微信小程序中经常会需要下拉页面进行更新要页面数据的功能,微信小程序提供了onPullDownRefresh函数。该函数作用是监听用户下拉动作。 一、onPullDown…...
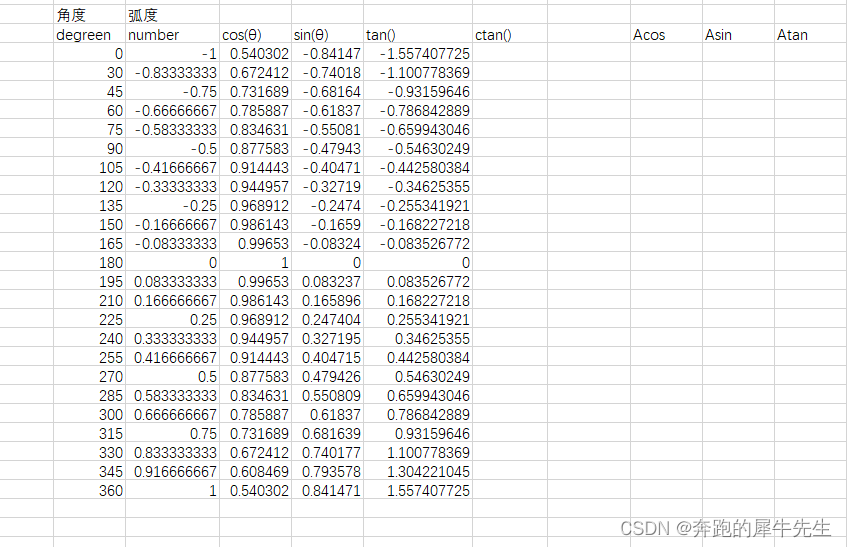
三角函数与圆,角度和弧度 (草稿,建设中)
目录 1 三角函数与圆,角度和弧度 1.1 三角形 1.2 圆形 2 角度 3 弧度 rad 4 角度,弧度的换算 2 三角函数 1 三角函数与圆,角度和弧度 1.1 三角形 角度弧长sin()cos()tan() 1.2 圆形 半径,周长,弧长半径面积 …...

AIGC 施展“物理魔法”,3D视觉突破“精度极限”
点击关注 文|姚悦,编|王一粟 “没有艺术,全是物理!物理让你快乐,不是吗?” 近日,在世界计算机图形会议 SIGGRAPH 2023 上,英伟达创始人、CEO 黄仁勋宣布,将…...
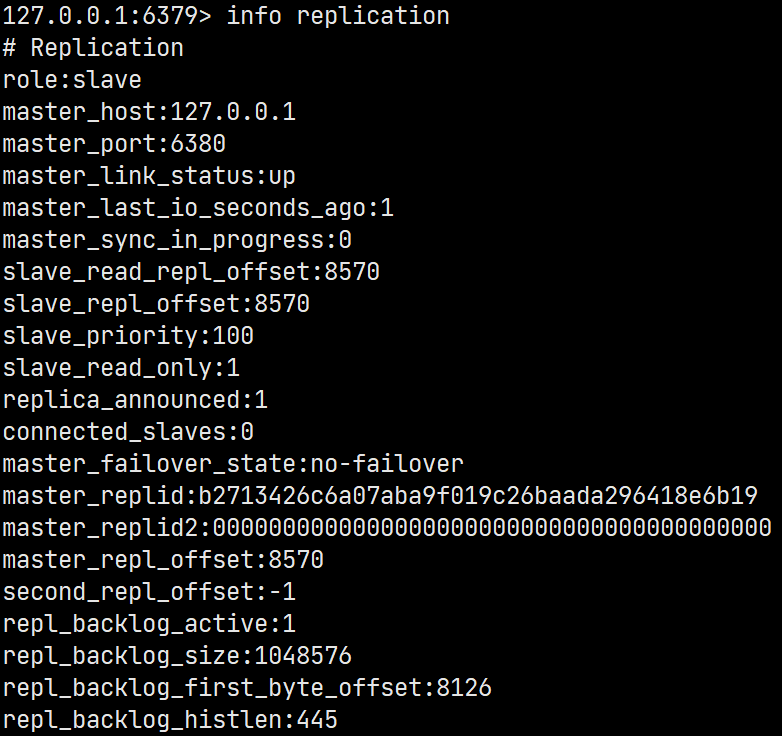
redis 哨兵模式
目录 一、什么是哨兵模式 二、配置哨兵 三、启动哨兵 四、验证哨兵 五、复制延时 六、选举策略 一、什么是哨兵模式 哨兵也叫 sentinel,它的作用是能够在后台监控主机是否故障,如果故障了根据投票数自动将从库转换为主库。 二、配置哨兵 首先停止…...
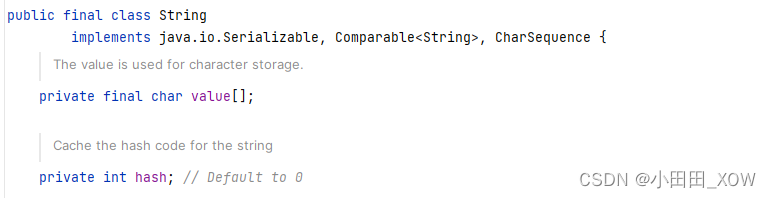
java八股文面试[java基础]——String StringBuilder StringBuffer
String类型定义: final String 不可以继承 final char [] 不可以修改 String不可变的好处: hash值只需要算一次,当String作为map的key时, 不需要考虑hash改变 天然的线程安全 知识来源: 【基础】String、StringB…...
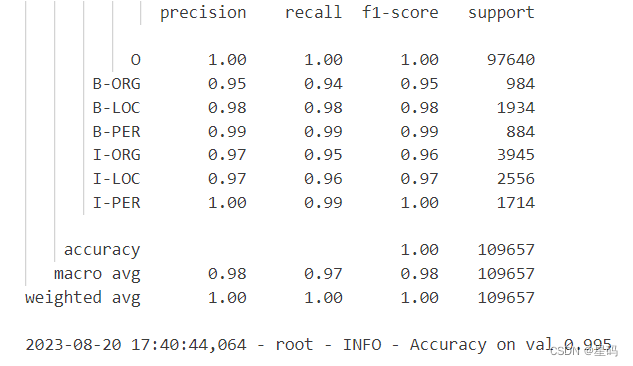
[oneAPI] 基于BERT预训练模型的命名体识别任务
[oneAPI] 基于BERT预训练模型的命名体识别任务 Intel DevCloud for oneAPI 和 Intel Optimization for PyTorch基于BERT预训练模型的命名体识别任务语料介绍数据集构建使用示例 命名体识别模型前向传播模型训练 结果 参考资料 比赛:https://marketing.csdn.net/p/f3…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
