当前位置： 首页 > news >正文

java高并发系列 - 第13天:JUC中的Condition对象

news 2026/2/8 15:51:08

java高并发系列 - 第13天:JUC中的Condition对象

java高并发系列第13篇文章

本文内容

  1. synchronized中实现线程等待和唤醒
  2. Condition简介及常用方法介绍及相关示例
  3. 使用Condition实现生产者消费者
  4. 使用Condition实现同步阻塞队列

Object对象中的wait()，notify()方法，用于线程等待和唤醒等待中的线程，大家应该比较熟悉，想再次了解的朋友可以移步到java高并发系列 - 第6天:线程的基本操作

synchronized中等待和唤醒线程示例

package com.ifly.accountservice.demo.thread;import java.util.concurrent.TimeUnit;public class Demo35 {static Object lock = new Object();public static class T1 extends Thread {@Overridepublic void run()

相关文章：

java高并发系列 - 第13天:JUC中的Condition对象

java高并发系列 - 第13天:JUC中的Condition对象 java高并发系列第13篇文章 本文内容 synchronized中实现线程等待和唤醒Condition简介及常用方法介绍及相关示例使用Condition实现生产者消费者使用Condition实现同步阻塞队列Object对象中的wait()，notify()方法，用于线程等待…...

编程日记 2023/8/22 7:26:09

【TTY子系统】printf与printk深入驱动解析

tty子系统解析 tty子系统是一个庞大且复杂，也是内核维护者所头大的子系统。 At a first glance, the TTY layer wouldn’t seem like it should be all that challenging. It is, after all, just a simple char device which is charged with transferring byte-o…...

编程日记 2023/8/22 7:25:08

无涯教程-PHP - 全局变量函数

全局变量 与局部变量相反,可以在程序的任何部分访问全局变量。通过将关键字 GLOBAL 放置在应被识别为全局变量的前面,可以很方便地实现这一目标。 <?php$somevar15;function addit() {GLOBAL $somevar;$somevar;print "Somevar is $somevar";}addit(); ?> …...

编程日记 2023/8/22 7:24:07

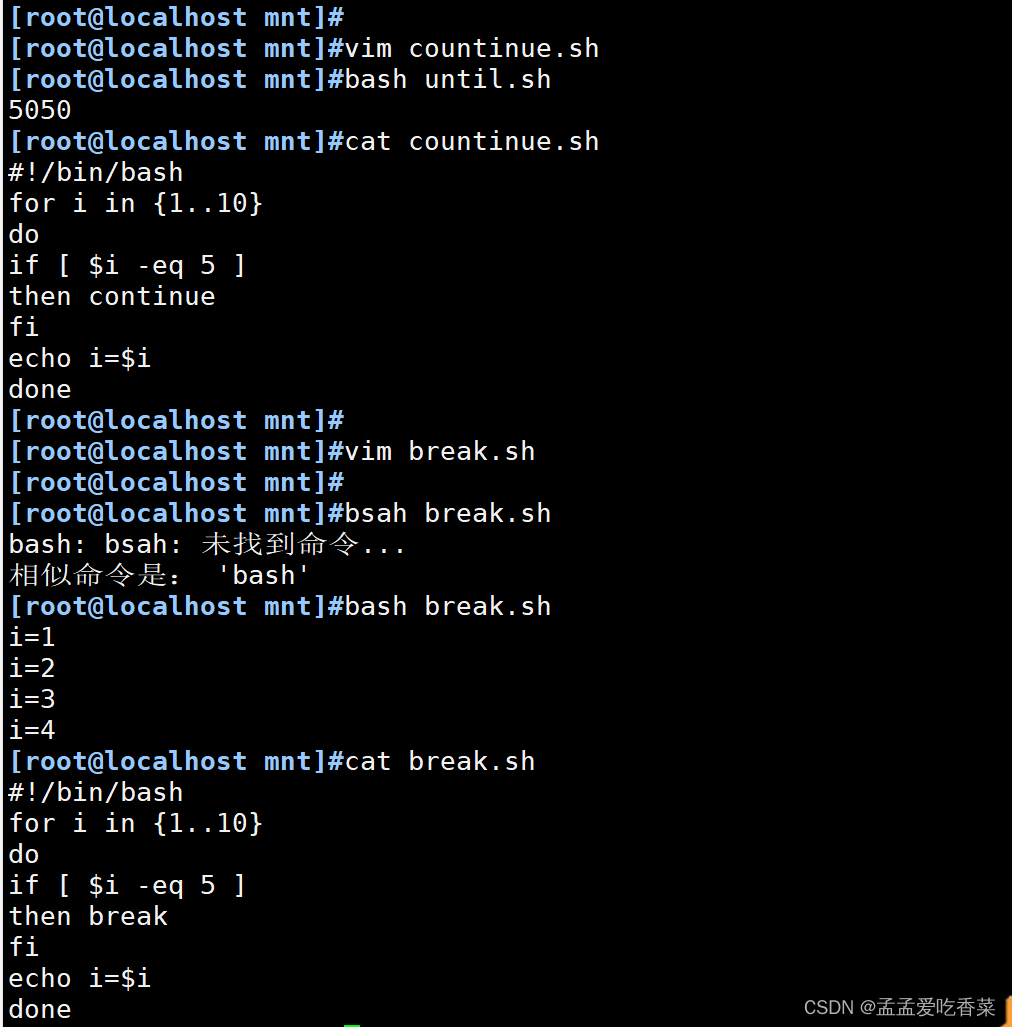
shell脚本之循环语句

循环语句 循环含义 将某代码段重复运行多次&#xff0c;通常有进入循环的条件和退出循环的条件 for循环语句 一般知道循环次数使用for循环 第一类 格式1&#xff1a; for名称 in 取值次数;do;done; 格式2&#xff1a; for 名称 in {取值列表} do done# 打印20次 for i i…...

编程日记 2023/8/22 7:23:05

派森 #P122. 峰值查找

描述 给定一个长度为n的列表nums&#xff0c;请你找到峰值并返回其索引。数组可能包含多个峰值&#xff0c;在这种情况下&#xff0c;返回任何一个所在位置即可。 &#xff08;1&#xff09;峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于&#xff1b; &…...

编程日记 2023/8/22 7:22:03

基础网络详解4--HTTP CookieSession 思考

一、cookie技术思考 一台多用户浏览器发起了三笔请求&#xff0c;将某款产品放入购物车中&#xff0c;A一次&#xff0c;选择了篮球&#xff1b;B两次&#xff0c;第一次选了足球&#xff0c;第二次选了钢笔。如何确认选择篮球、足球、钢笔的请求属于谁呢&#xff1f;如果不确认…...

编程日记 2023/8/22 7:21:01

14. 利用Canvas自制时钟组件

1. 说明 在自定义时钟组件时&#xff0c;使用到的基本控件主要是Canvas&#xff0c;在绘制相关元素时有两种方式&#xff1a;一种时在同一个canvas中绘制所有的部件元素&#xff0c;这样需要不断的对画笔和画布的属性进行保存和恢复&#xff0c;容易混乱&#xff1b;另一种就是…...

编程日记 2023/8/22 7:19:59

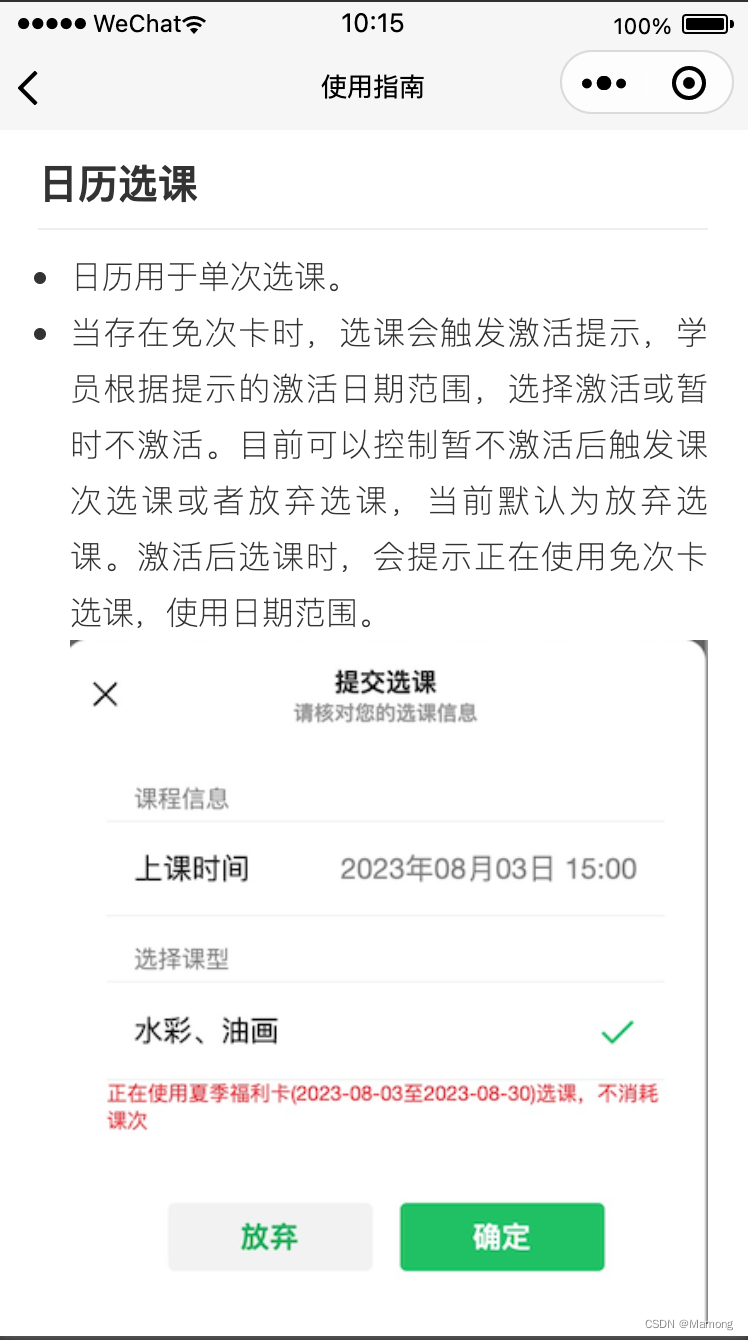
微信小程序使用云存储和Markdown开发页面

最近想在一个小程序里加入一个使用指南的页面&#xff0c;考虑到数据存储和减少页面的开发工作量&#xff0c;决定尝试在云存储里上传Markdown文件&#xff0c;微信小程序端负责解析和渲染。小程序端使用到一个库Towxml。 Towxml Towxml是一个可将HTML、Markdown转为微信小程…...

编程日记 2023/8/22 7:18:57

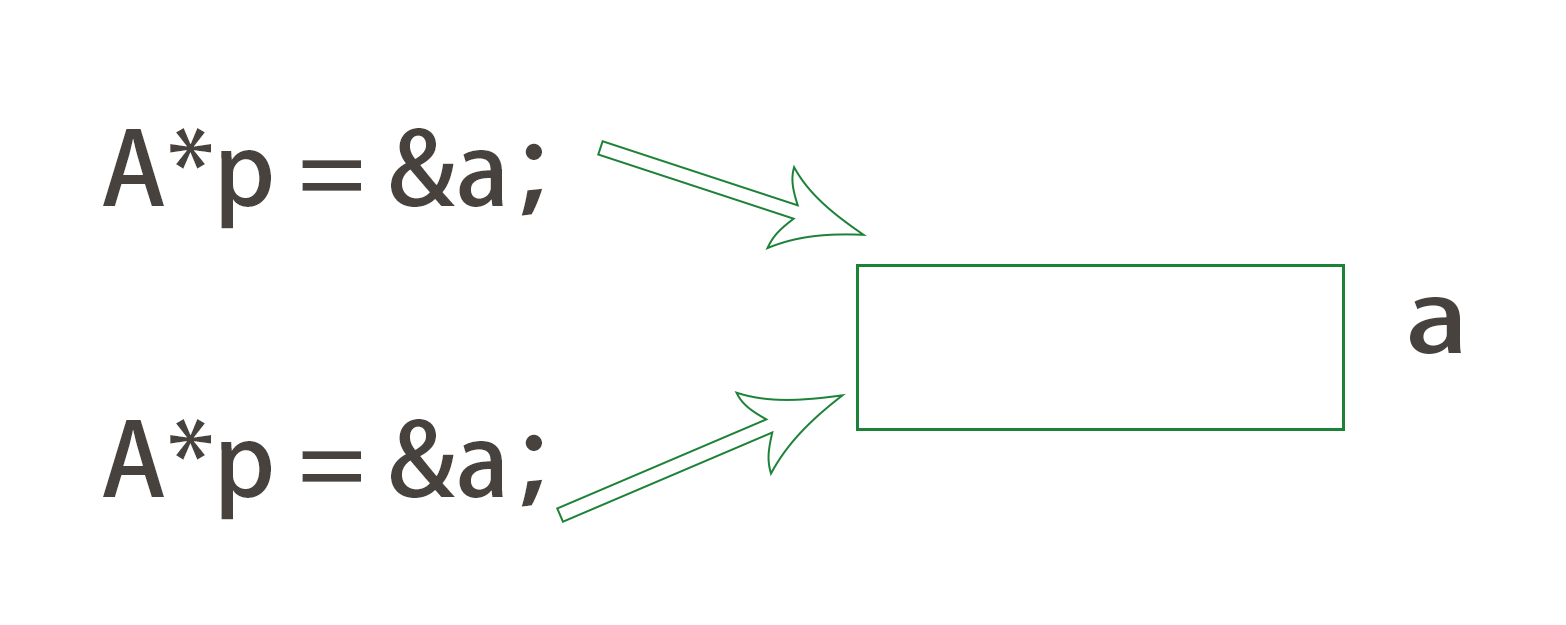
【C++】运算符重载 | 赋值运算符重载

Ⅰ. 运算符重载 引入 ❓什么叫运算符重载&#xff1f; 就是&#xff1a;运用函数&#xff0c;将现有的运算符重新定义&#xff0c;使其能满足各种自定义类型的运算。 回想一下&#xff0c;我们以前运算的对象是不是都是int、char这种内置类型&#xff1f; 那我们自定义的“…...

编程日记 2023/8/22 7:17:56

Python学习 -- 类对象从创建到常用函数

在Python编程中&#xff0c;类是一种强大的工具&#xff0c;用于创建具有共同属性和行为的对象。本篇博客将详细介绍Python中类和对象的创建&#xff0c;类的属性和方法&#xff0c;以及一些常用的类函数&#xff0c;通过丰富的代码例子来帮助读者深入理解。 一、类和对象的创…...

编程日记 2023/8/22 7:16:55

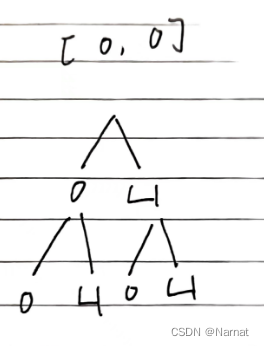
数组分割（2023省蓝桥杯）n种讨论 JAVA

目录 1、题目描述&#xff1a;2、前言&#xff1a;3、动态规划&#xff08;bug)&#xff1a;3、递归 剪枝&#xff08;超时&#xff09;&#xff1a;4、数学&#xff08;正解&#xff09;&#xff1a; 1、题目描述&#xff1a; 小蓝有一个长度为 N 的数组 A [A0, A1,…, AN−…...

编程日记 2023/8/22 7:15:52

很好的启用window10专业版系统自带的远程桌面

启用window10专业版系统自带的远程桌面 文章目录 启用window10专业版系统自带的远程桌面前言1.找到远程桌面的开关2. 找到“应用”项目3. 打开需要远程操作的电脑远程桌面功能 总结 前言 Windows操作系统作为应用最广泛的个人电脑操作系统&#xff0c;在我们身边几乎随处可见。…...

编程日记 2023/8/22 7:14:50

TCP定制协议，序列化和反序列化

目录 前言 1.理解协议 2.网络版本计算器 2.1设计思路 2.2接口设计 2.3代码实现&#xff1a; 2.4编译测试 总结 前言 在之前的文章中&#xff0c;我们说TCP是面向字节流的&#xff0c;但是可能对于面向字节流这个概念&#xff0c;其实并不理解的&#xff0c;今天我们要介…...

编程日记 2023/8/22 7:13:49

YOLOX在启智AI GPU/CPU平台部署笔记

文章目录 1. 概述2. 部署2.1 拉取YOLOX源码2.2 拉取模型文件yolox_s.pth2.3 安装依赖包2.4 安装yolox2.5 测试运行2.6 运行报错处理2.6.1 ImportError: libGL.so.1: cannot open shared object file: No such file or directory2.6.2 ImportError: libgthread-2.0.so.0: cannot…...

编程日记 2023/8/22 7:12:47

23种设计模式攻关

&#x1f44d;一、创建者模式 &#x1f516;1.1、单例模式 单例模式&#xff08;Singleton Pattern&#xff09;&#xff0c;用于确保一个类只有一个实例&#xff0c;并提供全局访问点。 在某些情况下&#xff0c;我们需要确保一个类只能有一个实例&#xff0c;比如数据库连接…...

编程日记 2023/8/22 7:11:46

【jsthreeJS】入门three，并实现3D汽车展示厅，附带全码

首先放个最终效果图&#xff1a; 三维&#xff08;3D&#xff09;概念&#xff1a; 三维&#xff08;3D&#xff09;是一个描述物体在三个空间坐标轴上的位置和形态的概念。相比于二维&#xff08;2D&#xff09;只有长度和宽度的平面&#xff0c;三维增加了高度或深度这一维度…...

编程日记 2023/8/22 7:10:44

unity将结构体/列表与json字符串相互转化

编写Unity程序时&#xff0c;面对大量需要传输或者保存的数据时&#xff0c;为了避免编写重复的代码&#xff0c;故采用NewtonJson插件来将定义好的结构体以及列表等转为json字符串来进行保存和传输。 具体代码如下&#xff1a; using System; using System.IO; using Newtons…...

编程日记 2023/8/22 7:09:43

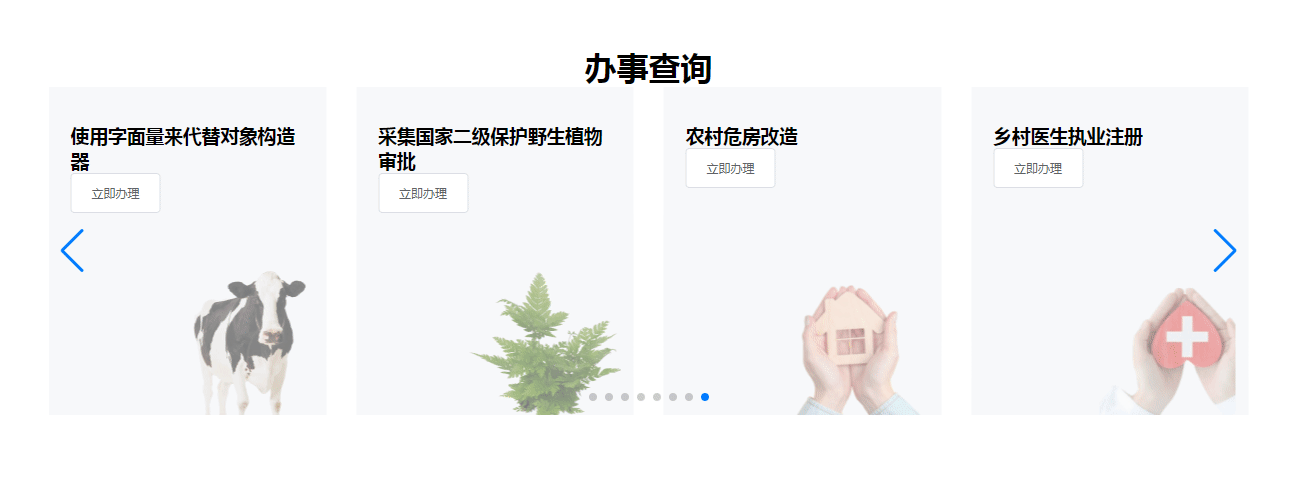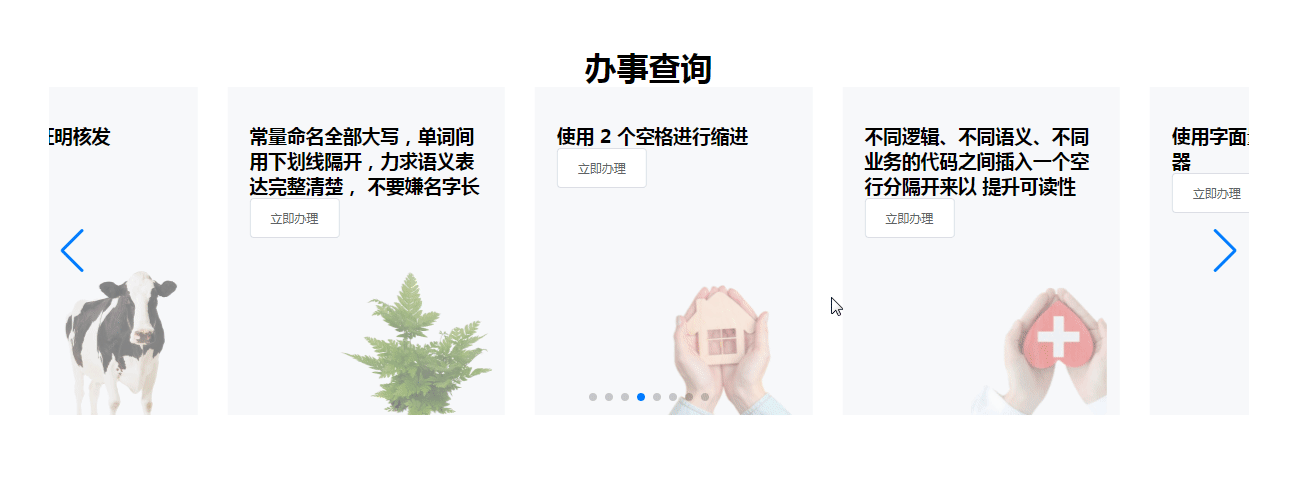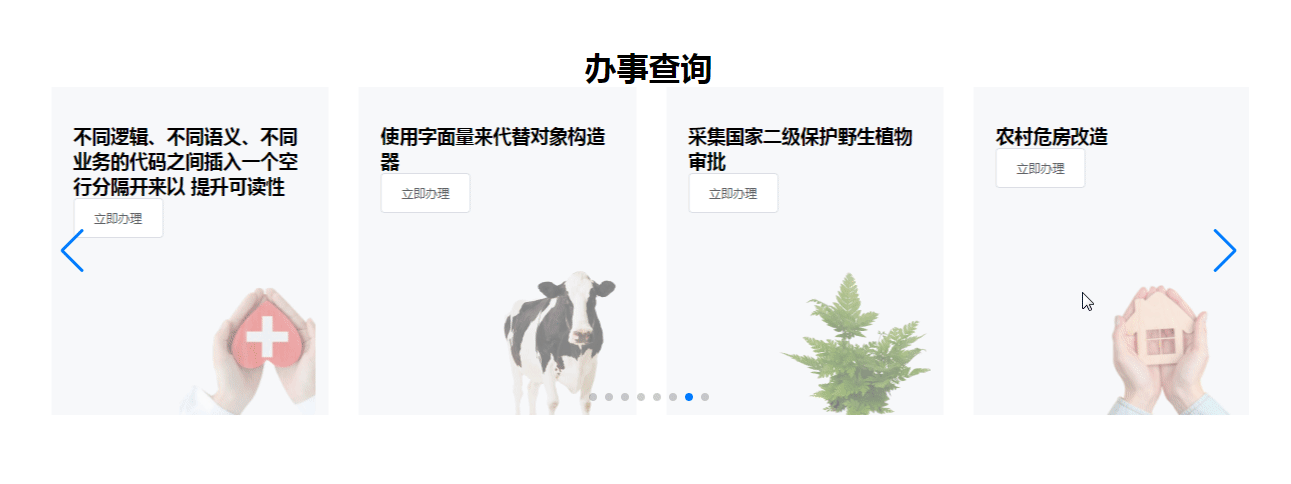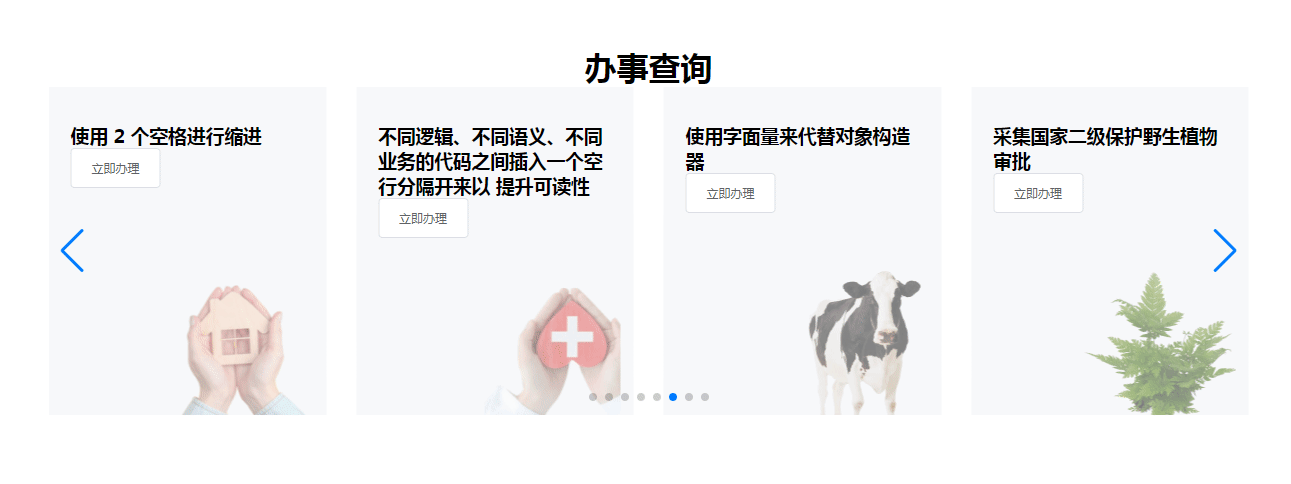
【Vue】vue2项目使用swiper轮播图2023年8月21日实战保姆级教程

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言一、npm 下载swiper二、使用步骤1.引入库声明变量2.编写页面3.执行js 总结 前言 swiper轮播图官网 参考文章&#xff0c;最好先看完他的介绍&#xff0c;再看…...

编程日记 2023/8/22 7:08:42

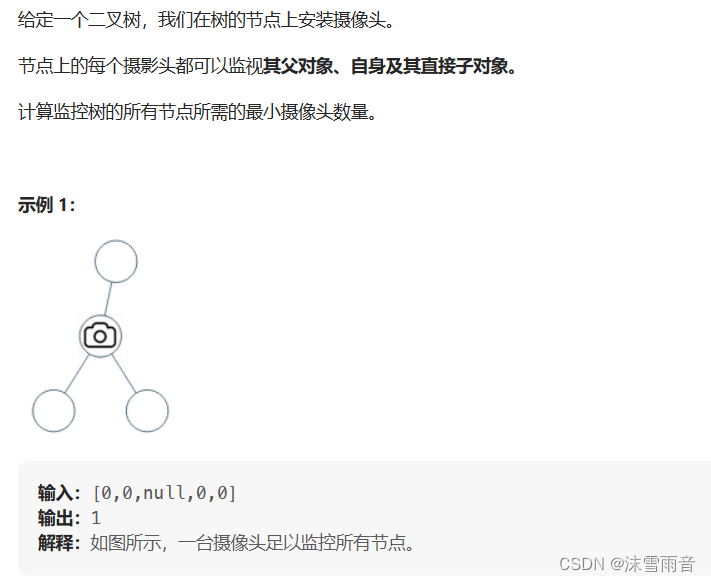
【算法日志】贪心算法刷题：单调递增数列，贪心算法总结(day32)

代码随想录刷题60Day 目录 前言 单调递增数列 贪心算法总结 前言 今天是贪心算法刷题的最后一天&#xff0c;今天本来是打算刷两道题&#xff0c;其中的一道hard题做了好久都没有做出来(主要思路错了)。然后再总结一下。 单调递增数列 int monotoneIncreasingDigits(int n…...

编程日记 2023/8/22 7:07:41

MATLAB算法实战应用案例精讲-【深度学习】模型压缩

目录 模型压缩概述 1. 为什么需要模型压缩 2. 模型压缩的基本方法 Patient-KD 1. Patient-KD 简介...

编程日记 2023/8/22 7:06:40

后进先出（LIFO）详解

LIFO 是 Last In, First Out 的缩写&#xff0c;中文译为后进先出。这是一种数据结构的工作原则&#xff0c;类似于一摞盘子或一叠书本&#xff1a; 最后放进去的元素最先出来 -想象往筒状容器里放盘子&#xff1a; &#xff08;1&#xff09;你放进的最后一个盘子&#xff08…...

编程新知 2026/2/8 1:22:58

利用最小二乘法找圆心和半径

#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

编程新知 2026/2/8 4:37:37

基于大模型的 UI 自动化系统

基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

编程新知 2025/10/22 11:16:20

DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径

目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

编程新知 2025/11/20 2:48:44

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2026/2/2 22:06:13

排序算法总结（C++）

目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指&#xff1a;同样大小的样本 **&#xff08;同样大小的数据&#xff09;**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

编程新知 2026/1/25 9:33:23

scikit-learn机器学习

# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

编程新知 2026/2/1 17:50:36

给网站添加live2d看板娘

给网站添加live2d看板娘 参考文献&#xff1a; stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下&#xff0c;文章也主…...

编程新知 2026/2/1 4:23:19

认识CMake并使用CMake构建自己的第一个项目

1.CMake的作用和优势 跨平台支持&#xff1a;CMake支持多种操作系统和编译器&#xff0c;使用同一份构建配置可以在不同的环境中使用 简化配置&#xff1a;通过CMakeLists.txt文件&#xff0c;用户可以定义项目结构、依赖项、编译选项等&#xff0c;无需手动编写复杂的构建脚本…...

编程新知 2026/2/7 19:54:51

链式法则中 复合函数的推导路径 多变量“信息传递路径”

非常好&#xff0c;我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题&#xff0c;统一使用 二重复合函数&#xff1a; z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y))​ 来全面说明。我们会展示其全微分形式&#xff08;偏导…...

编程新知 2026/2/8 12:07:50