数组分割(2023省蓝桥杯)n种讨论 JAVA
目录
- 1、题目描述:
- 2、前言:
- 3、动态规划(bug):
- 3、递归 + 剪枝(超时):
- 4、数学(正解):
1、题目描述:
小蓝有一个长度为 N 的数组 A = [A0, A1,…, AN−1]。现在小蓝想要从 A 对应的数组下标所构成的集合 I = {0, 1,
2, . . . , N − 1} 中找出一个子集 R1,那么 R1在 I 中的补集为 R2。记 S1=∑r∈R1Ar,S2
=∑r∈R2Ar,我们要求 S1 和 S2 均为偶数,请问在这种情况下共有多少种不同的 R1。当 R1 或 R2 为空集时我们将 S1 或 S2 视为 0。 输入格式 第一行一个整数 T,表示有 T 组数据。 接下来输入 T 组数据,每组数据包含两行:第一行一个整数 N,表示数组
A 的长度;第二行输入 N 个整数从左至右依次为 A0, A1, . . . , AN−1,相邻元素之间用空格分隔。 输出格式
对于每组数据,输出一行,包含一个整数表示答案,答案可能会很大,你需要将答案对1000000007 进行取模后输出。
样例输入:
2
2
6 6
2
1 6
样例输出:
4
0
[提示]
对于第一组数据,答案为 4。(注意:大括号内的数字表示元素在数组中的下标。)
R1 = {0}, R2 = {1};此时 S1 = A0 = 6 为偶数, S2 = A1 = 6 为偶数。
R1 = {1}, R2 = {0};此时 S1 = A1 = 6 为偶数, S2 = A0 = 6 为偶数。
R1 = {0, 1}, R2 = {};此时 S1 = A0 + A1 = 12 为偶数, S2 = 0 为偶数。
R1 = {}, R2 = {0, 1};此时 S1 = 0 为偶数, S2 = A0 + A1 = 12 为偶数。
对于第二组数据,无论怎么选择,都不满足条件,所以答案为 0。
对于 20% 的评测用例,1 ≤ N ≤ 10。
对于 40% 的评测用例,1 ≤ N ≤ 10^2。
对于 100% 的评测用例,1 ≤ T ≤ 10, 1 ≤ N ≤ 103 , 0 ≤ Ai ≤ 10^9。
2、前言:
这题考完蓝桥杯之后,自闭地看着答案整理过一遍,当时一度认为只能用数学方法做,而且当时也意识到自己见识太少,所以这俩月一直在埋头苦刷暂避锋芒。这不,这两天感觉自己又行了再来回顾本题,看看能否用新的算法做,以下是思考结果:
3、动态规划(bug):
最开始想到的就是用动态规划解决本题,虽然动态规划学的不熟,但是有思路就能写出来,本题还是不建议用动态规划解因为题目给的数据太大,非常容易爆数组。
1、本题与01背包有些许相似所以用01背包思想试解
2、dp[ i ][ j ] = n即:考虑前i个元素挑选出的元素和为j的方案数为n
3、初始化dp[i][0] = 1,考虑前i个元素,和为0的方案数为什么都不选1种
4、对于元素i无非选与不选两种,dp[i][j]=dp[i - 1][j] + dp[i - 1][j - nums[j]],前提是j >= nums[j]
5、最后取所有dp[len][j]且j是偶数的元素即可
错误代码1:
import java.util.*;public class Text2{//继承父类Jframe,获取父类方法public static int mod = 1000000007;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();for(int i = 0; i < n; i ++) {int len = sc.nextInt();int nums[] = new int[len + 1];for(int j = 1; j <= len; j ++) nums[j] = sc.nextInt();System.out.println(dfs(nums, len));}}public static int dfs(int nums[], int len) {int num = 0;for(int j = 1; j <= len; j ++) num = num + nums[j];if(num % 2 != 0) return 0;int dp[][] = new int[len + 1][num + 1];for(int i = 0; i <= len; i ++) dp[i][0] = 1;int cnt = 1;for(int i = 1; i <= len; i ++) {for(int j = 1; j <= num; j ++) {dp[i][j] = dp[i - 1][j]; if(j >= nums[i])dp[i][j] = dp[i][j] + dp[i - 1][j - nums[i]];if(i == len && j % 2 == 0) {cnt = cnt + dp[i][j];System.out.println(i + " " + j + " " + dp[i][j]);}}}return cnt;}}
想着用一维数组优化
错误代码1优化版:
import java.util.*;public class Text1{//继承父类Jframe,获取父类方法public static int mod = 1000000007;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();for(int i = 0; i < n; i ++) {int len = sc.nextInt();int nums[] = new int[len + 1];for(int j = 1; j <= len; j ++) nums[j] = sc.nextInt();System.out.println(dfs(nums, len));}}public static int dfs(int nums[], int len) {int num = 0;for(int j = 1; j <= len; j ++) num = num + nums[j];if(num % 2 != 0) return 0;int dp[] = new int[num + 1];dp[0] = 1;//考虑前0件元素得到0的方法有1个int cnt = 1;for(int j = 1; j <= len; j ++)//考虑前len个元素for(int z = num; z >= nums[j]; z --){dp[z] = dp[z] + dp[z - nums[j]];if(j == len && z % 2 == 0 && (num - z) % 2 == 0) cnt = (cnt + dp[z]) % mod;}return cnt;}}
解题思路:
为什么看着思路没问题题,但却还是错误代码呢,因为题目的数据含有0!!!
以正常没有0的[2, 4]为例子:
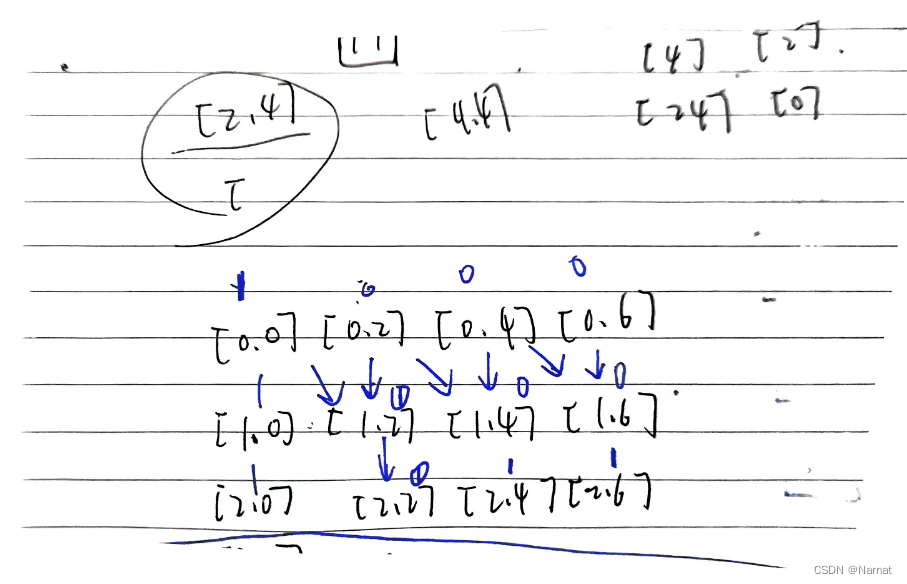
动态规划需要通过数组迭代,对于元素i无非就是选与不选但当元素nums[i] = 0的时候,选了与没选是不确定的其无法从初始dp[0][0]迭代过来以有0的[0, 2]为例子:
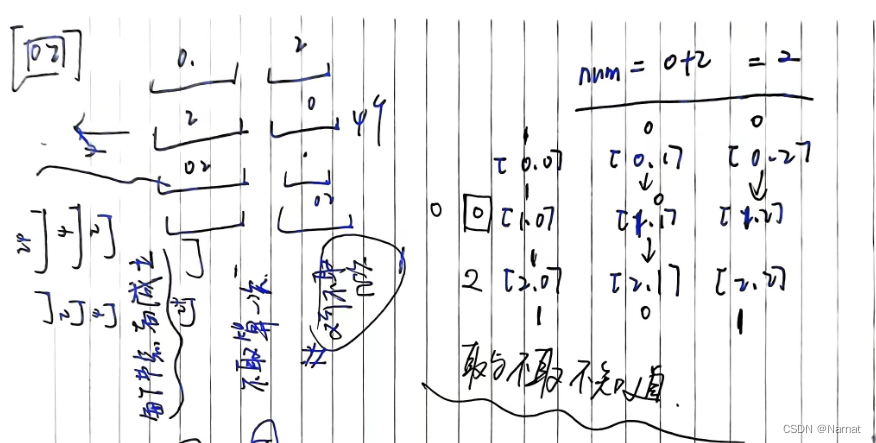
元素无法从dp[0][0]迭代出去,形成了不通路。
值得一提的是优化代码错误更多
以[2, 2, 4]为例,未优化与优化代码数组迭代过程如下:

由于一维数组从后往前遍历dp[3][2]虽然符合条件但是无法从dp[2][2]迭代下来(2 < 4)
如果数据范围>0的话动态规划还是能在不爆数组的情况下都对的以下是产生随机数据的代码以及测试结果
代码:
import java.awt.print.Printable;
import java.util.*;public class Text4{public static int mod = 1000000007;public static void main(String[] args) { for(int i = 0; i < 1000; i ++) {Scanner sc = new Scanner(System.in);int len = new Random().nextInt(1000) + 1;
// int len = sc.nextInt();int nums[] = new int[len + 1];for(int j = 1; j <= len; j ++)
// nums[j] = sc.nextInt();nums[j] = new Random().nextInt(1000) + 1;boolean flag = (dfs(nums, len) == ddffs(nums, len));System.out.println(flag);if(!flag) {print(nums, dfs(nums, len), ddffs(nums, len));return;}}}public static int dfs(int nums[], int len) {int num = 0;for(int j = 1; j <= len; j ++) num = num + nums[j];if(num % 2 != 0) return 0;int dp[][] = new int[len + 1][num + 1];for(int i = 0; i <= len; i ++) dp[i][0] = 1;int cnt = 1;for(int i = 1; i <= len; i ++)for(int j = 1; j <= num; j ++) {dp[i][j] = dp[i - 1][j]; if(j >= nums[i])dp[i][j] = (dp[i][j] + dp[i - 1][j - nums[i]]) % mod;if(i == len && j % 2 == 0) cnt = (cnt + dp[i][j]) % mod;}return cnt;}public static int ddffs(int a[], int m) {int L = 0, J = 0; for(int i = 1; i <= m; i ++) if(a[i] % 2 == 0) L ++;else J ++;if(J % 2 != 0) return 0;else {if(J == 0) J = 1;return (int)(Math.pow(2, L) * Math.pow(2, J - 1) % mod);}}public static void print(int a[], int b, int c) {System.out.println(a.length - 1 + " " + b + " " + c);for(int i = 1; i < a.length; i ++) System.out.print(a[i] + " ");}
}

好动态规划到此宣布破产
3、递归 + 剪枝(超时):
考试的时候就是用递归做的,但是太傻比了,退出条件不对,我早就应该知道递归的每条路径就是一种遍历情况,当时以及昨天我却在分枝上找答案太傻逼了,答案应该在递归末尾节点找。
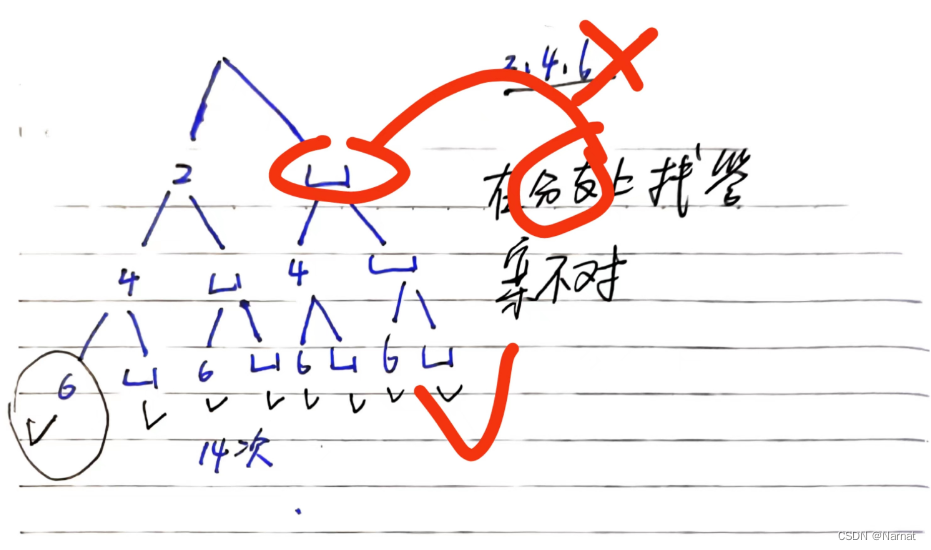
太傻比了之前用递归一直是在分支上找答答案,跟本没啥意义,再加上有0的出现我一直以为本题不能用常规递归做,用什么分治思想之类的。。。刚在才醒悟过来,把递归图画了以下才醒悟,根本没必要那么复杂直接在递归末尾节点判断就行了
每个元素都是选与不选两种情况,从首节点到任意末尾节点都是一条路径,本题来说是选元素的其中一种选法,只需要判断满不满足题意就行了,太傻比了希望以后不要再犯这种错误了!
代码:
import java.util.Scanner;public class Text6 {//继承父类Jframe,获取父类方法public static int mod = 1000000007;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int m = sc.nextInt();for(int j = 0; j < m; j ++) {long sum = 0;int n = sc.nextInt();int nums[] = new int[n];for(int i = 0; i < n; i ++) {nums[i] = sc.nextInt();sum = sum + nums[i];}if(sum % 2 == 0)System.out.println(dfs(nums, n, 0, 0));elseSystem.out.println(0);}}public static int dfs(int nums[], int len, int i, long sum) {if(i == len) {if(sum % 2 == 0) return 1;return 0;}int choosethis = dfs(nums, len, i + 1, sum + nums[i]) % mod;int notchoose = dfs(nums, len, i + 1, sum) % mod;return (choosethis + notchoose) % mod;}}

超时是意料之内,剪一下枝即可
优化代码:
用二维数组可能会爆掉,用大杀器其map应该就能拿下本题:
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;public class Text7 { public static Map<String, Integer> map;public static int mod = 1000000007;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int m = sc.nextInt();for(int j = 0; j < m; j ++) {map = new HashMap<String, Integer>();long sum = 0;int n = sc.nextInt();int nums[] = new int[n];for(int i = 0; i < n; i ++) {nums[i] = sc.nextInt();sum = sum + nums[i];}if(sum % 2 == 0)System.out.println(dfs(nums, n, 0, 0));elseSystem.out.println(0);}}public static int dfs(int nums[], int len, int i, long sum) {if(map.containsKey(i + " " + sum)) return map.get(i + " " + sum);if(i == len) {if(sum % 2 == 0) return 1;return 0;}int choosethis = dfs(nums, len, i + 1, sum + nums[i]) % mod;int notchoose = dfs(nums, len, i + 1, sum) % mod;map.put(i + " " + sum, (choosethis + notchoose) % mod);return (choosethis + notchoose) % mod;}}
看一下成果!

我真是热烈的🐎测了好几遍一个样,要么测试的地方不行,要么map查表和剪纸的部分正负得零,反正麻了
算了不重要了,最后再说一下为什么递归不会被0影响,这从递归图可以看出来
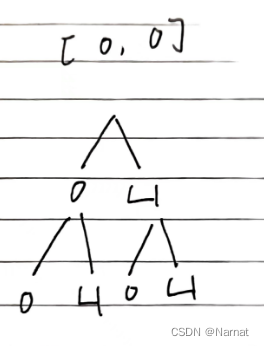
递归每条路径都是一个选择情况,即使两个0也可以清楚看出所有情况。
4、数学(正解):
详细解析在这里:
2023年第十四届蓝桥杯JavaB组省赛真题及解析
相关文章:

数组分割(2023省蓝桥杯)n种讨论 JAVA
目录 1、题目描述:2、前言:3、动态规划(bug):3、递归 剪枝(超时):4、数学(正解): 1、题目描述: 小蓝有一个长度为 N 的数组 A [A0, A1,…, AN−…...
很好的启用window10专业版系统自带的远程桌面
启用window10专业版系统自带的远程桌面 文章目录 启用window10专业版系统自带的远程桌面前言1.找到远程桌面的开关2. 找到“应用”项目3. 打开需要远程操作的电脑远程桌面功能 总结 前言 Windows操作系统作为应用最广泛的个人电脑操作系统,在我们身边几乎随处可见。…...

TCP定制协议,序列化和反序列化
目录 前言 1.理解协议 2.网络版本计算器 2.1设计思路 2.2接口设计 2.3代码实现: 2.4编译测试 总结 前言 在之前的文章中,我们说TCP是面向字节流的,但是可能对于面向字节流这个概念,其实并不理解的,今天我们要介…...

YOLOX在启智AI GPU/CPU平台部署笔记
文章目录 1. 概述2. 部署2.1 拉取YOLOX源码2.2 拉取模型文件yolox_s.pth2.3 安装依赖包2.4 安装yolox2.5 测试运行2.6 运行报错处理2.6.1 ImportError: libGL.so.1: cannot open shared object file: No such file or directory2.6.2 ImportError: libgthread-2.0.so.0: cannot…...

23种设计模式攻关
👍一、创建者模式 🔖1.1、单例模式 单例模式(Singleton Pattern),用于确保一个类只有一个实例,并提供全局访问点。 在某些情况下,我们需要确保一个类只能有一个实例,比如数据库连接…...
【jsthreeJS】入门three,并实现3D汽车展示厅,附带全码
首先放个最终效果图: 三维(3D)概念: 三维(3D)是一个描述物体在三个空间坐标轴上的位置和形态的概念。相比于二维(2D)只有长度和宽度的平面,三维增加了高度或深度这一维度…...

unity将结构体/列表与json字符串相互转化
编写Unity程序时,面对大量需要传输或者保存的数据时,为了避免编写重复的代码,故采用NewtonJson插件来将定义好的结构体以及列表等转为json字符串来进行保存和传输。 具体代码如下: using System; using System.IO; using Newtons…...
【Vue】vue2项目使用swiper轮播图2023年8月21日实战保姆级教程
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、npm 下载swiper二、使用步骤1.引入库声明变量2.编写页面3.执行js 总结 前言 swiper轮播图官网 参考文章,最好先看完他的介绍,再看…...
【算法日志】贪心算法刷题:单调递增数列,贪心算法总结(day32)
代码随想录刷题60Day 目录 前言 单调递增数列 贪心算法总结 前言 今天是贪心算法刷题的最后一天,今天本来是打算刷两道题,其中的一道hard题做了好久都没有做出来(主要思路错了)。然后再总结一下。 单调递增数列 int monotoneIncreasingDigits(int n…...

MATLAB算法实战应用案例精讲-【深度学习】模型压缩
目录 模型压缩概述 1. 为什么需要模型压缩 2. 模型压缩的基本方法 Patient-KD 1. Patient-KD 简介...

Matlab使用
Matlab使用 界面介绍 新建脚本:实际上就是新建一个新建后缀为.m的文件 新建编辑器:ctrlN 打开:打开最近文件,以找到最近写过的文件 点击路径,切换当前文件夹 预设:定制习惯用的界面 常见简单指令 ;…...
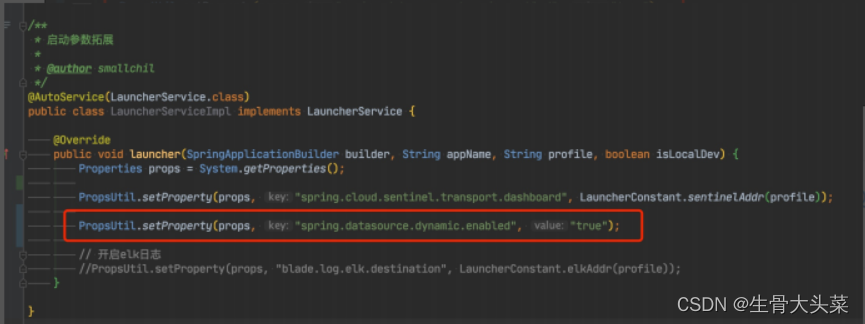
BladeX多数据源配置
启用多租户数据库隔离,会默认关闭mybatis-plus多数据源插件的启动,从而使用自定义的数据源识别 若不需要租户数据库隔离只需要字段隔离,而又需要用到多数据源的情况,需要前往LauncherService单独配置 数据源切换失败 详情请看说明…...

go里面关于超时的设计
设想一下你在接收源源不断的数据,如果有700ms没有收到,则认为是一个超时,需要做出处理。 逻辑上可以设计一个grouting,里面放一个通道,每收到一条数据进行相应处理。通道中夹杂一个timer定时器的处理,若通道在700ms内…...
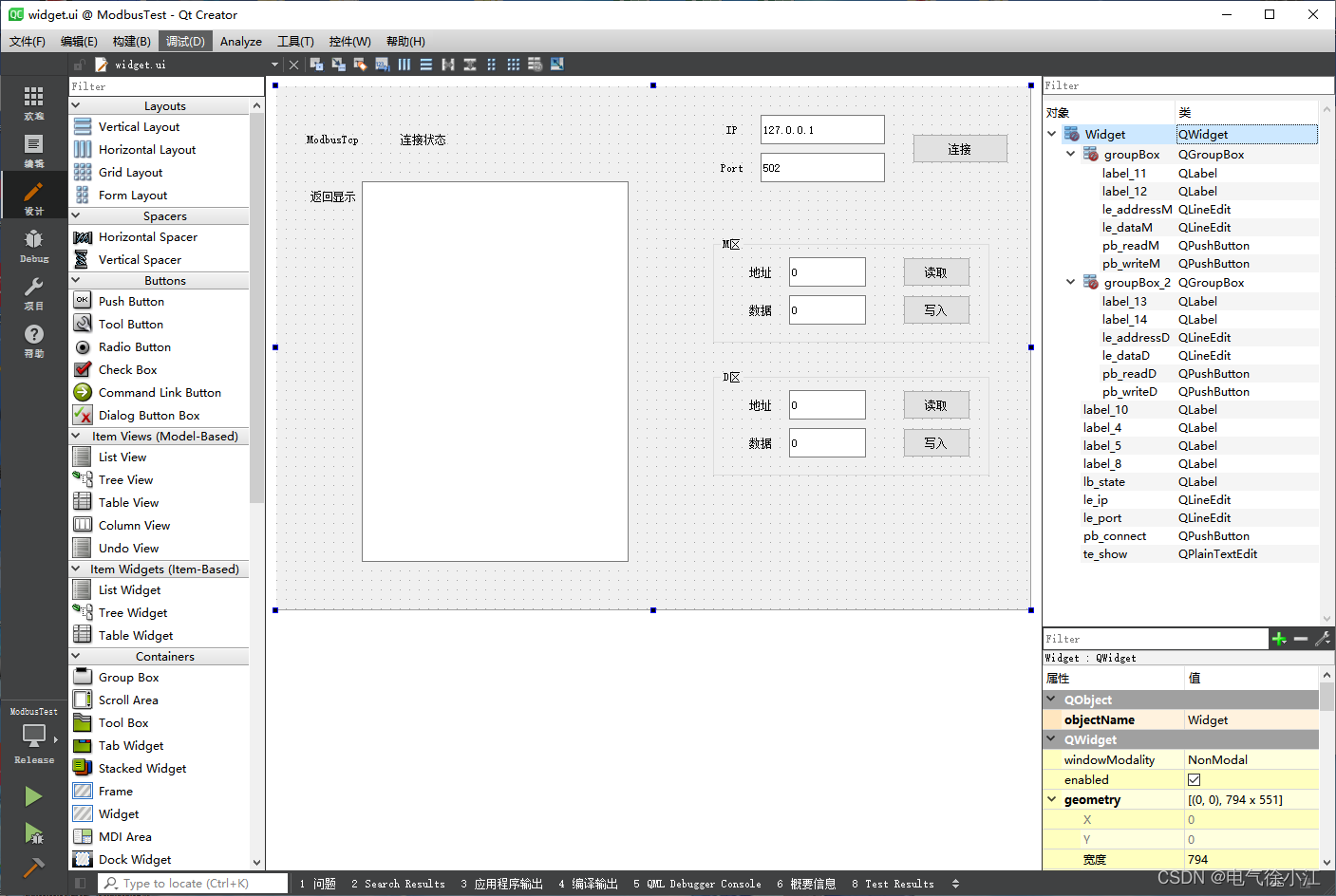
Qt下使用ModbusTcp通信协议进行PLC线圈/保持寄存器的读写(32位有符号数)
文章目录 前言一、引入Modbus模块二、Modbus设备的连接三、各寄存器数据的读取四、各寄存器数据的写入五、示例完整代码总结 前言 本文主要讲述了使用Qt的Modbus模块来进行ModbusTcp的通信,实现对PLC的线圈寄存器和保持寄存器的读写,基于TCP/IP的Modbus…...
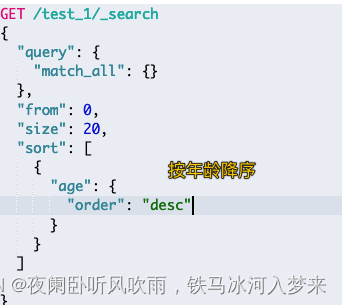
ElasticSearch学习2
1、索引的操作 1、创建索引 对ES的操作其实就是发送一个restful请求,kibana中在DevTools中进行ES操作 创建索引时需要注意ES的版本,不同版本的ES创建索引的语句略有差别,会导致失败 如下创建一个名为people的索引,settings&…...

3D角色展示
先看效果: 再看代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>3D卡片悬停</title><style>font-face {font-family: "Exoct";src: url("htt…...

前端面试:【Angular】打造强大Web应用的全栈框架
嗨,亲爱的Angular探险家!在前端开发的旅程中,有一个全栈框架,那就是Angular。Angular提供了模块化、组件化、依赖注入、路由和RxJS等特性,助力你构建强大、可扩展的Web应用。 1. 什么是Angular? Angular是…...

数据结构:栈和队列
文章目录 一、栈1.栈的概念及结构1.栈的概念及结构2.栈的实现 2.栈的顺序表实现1.栈的结构体和实现的功能函数2.栈的初始化,入栈和出栈操作3.栈的其他操作 3.栈的链表实现1.栈的结构体和实现的功能函数2.栈功能函数的实现 二、队列1.队列的概念及结构1.队列的概念及…...

SpringCloud Gateway服务网关的介绍与使用
目录 1、网关介绍2、SpringCloudGateway工作原理3、三大组件3.1 、Route(路由)3.2、断言 Predicate3.3、过滤器 filter 4、Gateway整合nacos的使用4.1 、引入依赖4.2、 编写基础类和启动类4.3、 编写基础配置和路由规则4.4 、测试结果 1、网关介绍 客户…...

深入解析:如何打造高效的直播视频美颜SDK
在当今数字化时代,视频直播已经成为人们交流、娱乐和信息传递的重要方式。然而,许多人在直播时都希望能够呈现出最佳的外观,这就需要高效的直播视频美颜技术。本文将深入解析如何打造高效的直播视频美颜SDK,以实现令人满意的视觉效…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
