Numpy入门(3)—线性代数
线性代数
线性代数(如矩阵乘法、矩阵分解、行列式以及其他方阵数学等)是任何数组库的重要组成部分,NumPy中实现了线性代数中常用的各种操作,并形成了numpy.linalg线性代数相关的模块。本节主要介绍如下函数:
diag:以一维数组的形式返回方阵的对角线(或非对角线)元素,或将一维数组转换为方阵(非对角线元素为0)。dot:矩阵乘法。trace:计算对角线元素的和。det:计算矩阵行列式。eig:计算方阵的特征值和特征向量。inv:计算方阵的逆。
向量与矩阵:
矩阵:有多行多列元素组成的一个集合,一个m*n的矩阵,有m行n列个元素
向量:如果一个矩阵只有一列,那么就是一个列向量;如果只有一行,那么就是一个行向量
从某个角度来说,矩阵就是由多个向量组成的
矩阵相乘:
A矩阵:m行
B矩阵:n列
前提:m=n
C矩阵:AB乘积
- 乘积C的第m行、n列 = 矩阵A的第m行的元素与矩阵B第n列元素的乘积之和
# 矩阵相乘
a = np.arange(12)
b = a.reshape([3, 4])
c = a.reshape([4, 3])
# 矩阵b的第二维大小,必须等于矩阵c的第一维大小
d = b.dot(c) # 等价于 np.dot(b, c)
print('a: \n{}'.format(a))
print('b: \n{}'.format(b))
print('c: \n{}'.format(c))
print('d: \n{}'.format(d))
a:
[ 0 1 2 3 4 5 6 7 8 9 10 11]
b:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
c:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
d:
[[ 42 48 54]
[114 136 158]
[186 224 262]]
# numpy.linalg 中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西
# np.linalg.diag 以一维数组的形式返回方阵的对角线(或非对角线)元素,
# 或将一维数组转换为方阵(非对角线元素为0)
e = np.diag(d)
f = np.diag(e)
print('d: \n{}'.format(d))
print('e: \n{}'.format(e))
print('f: \n{}'.format(f))
d:
[[ 42 48 54]
[114 136 158]
[186 224 262]]
e:
[ 42 136 262]
f:
[[ 42 0 0]
[ 0 136 0]
[ 0 0 262]]
# trace, 计算对角线元素的和
g = np.trace(d)
g
440
# det,计算行列式
h = np.linalg.det(d)
h
1.3642420526593978e-11
# eig,计算特征值和特征向量
i = np.linalg.eig(d)
i
(array([4.36702561e+02, 3.29743887e+00, 3.13152204e-14]), array([[ 0.17716392, 0.77712552, 0.40824829], [ 0.5095763 , 0.07620532, -0.81649658], [ 0.84198868, -0.62471488, 0.40824829]]))
# inv,计算方阵的逆
tmp = np.random.rand(3, 3)
j = np.linalg.inv(tmp)
j
array([[-0.59449952, 1.39735912, -0.06654123], [ 1.56034184, -0.40734618, -0.48055062], [ 0.10659811, -0.62164179, 1.30437759]])
补充:矩阵的逆
矩阵的逆是指对于一个n维的矩阵A,存在一个n维的矩阵B,使得A乘以B等于单位矩阵E,即AB=BA=E。其逆矩阵求解方法,有以下几种:
伴随矩阵法: 伴随矩阵法是求解矩阵逆的一种方法。对于一个n维矩阵A,其逆矩阵可以用下式表示:A^(-1)=1/|A| * Adj(A),其中|A|表示A的行列式,Adj(A)表示A的伴随矩阵。伴随矩阵的求法是:先求出矩阵A的代数余子式,然后将其转置得到的矩阵即为伴随矩阵。
初等变换法: 初等变换法是求解矩阵逆的另一种方法。将待求逆的矩阵A和单位矩阵E按行合并成一个矩阵[A|E],然后对其进行初等变换,直到左边的矩阵变为单位矩阵,右边的矩阵即为所求的逆矩阵。
高斯-约旦消元法: 高斯-约旦消元法也是求解矩阵逆的一种方法。将待求逆的矩阵A和单位矩阵E按列合并成一个矩阵[A|E],然后对其进行高斯-约旦消元,直到左边的矩阵变为单位矩阵,右边的矩阵即为所求的逆矩阵。
分块矩阵法: 分块矩阵法适用于分块矩阵的求逆,即将一个大的矩阵分成多个小的矩阵。其方法是将大矩阵A分成四个小矩阵A11、A12、A21、A22,并根据矩阵分块公式求出逆矩阵。
代码合集
import numpy as npdef func1():a = np.arange(12)b = a.reshape([3, 4])c = a.reshape([4, 3])# 矩阵b的第二维大小,必须等于矩阵c的第一维大小d = b.dot(c) # 等价于 np.dot(b, c)# np.dot(b, c)print('a: \n{}'.format(a))print('b: \n{}'.format(b))print('c: \n{}'.format(c))print('d: \n{}'.format(d))# numpy.linalg 中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西# np.linalg.diag 以一维数组的形式返回方阵的对角线(或非对角线)元素,# 或将一维数组转换为方阵(非对角线元素为0)print("=========linalg test=========")e = np.diag(d)f = np.diag(e)print('d: \n{}'.format(d))print('e: \n{}'.format(e))print('f: \n{}'.format(f))# 计算对角线元素之和g = np.trace(d)print(g)# det,计算行列式h = np.linalg.det(d)print(h)# eig,计算特征值和特征向量i = np.linalg.eig(d)print(i)def func2():# 计算方阵的逆# https://blog.51cto.com/u_15072903/3963066tmp = np.random.rand(3, 3)print(tmp)j = np.linalg.inv(tmp)print(j)print(tmp.dot(j))print(j.dot(tmp))if __name__ == "__main__":# func1()func2()相关文章:
—线性代数)
Numpy入门(3)—线性代数
线性代数 线性代数(如矩阵乘法、矩阵分解、行列式以及其他方阵数学等)是任何数组库的重要组成部分,NumPy中实现了线性代数中常用的各种操作,并形成了numpy.linalg线性代数相关的模块。本节主要介绍如下函数: diag&am…...

php的openssl_encrypt是不是自动做了PKCS5Padding?
在PHP中,openssl_encrypt函数默认使用的是PKCS7填充(不是PKCS5填充)。PKCS7填充实际上是PKCS5填充的扩展,用于对不同块大小的数据进行填充。 当你使用openssl_encrypt函数进行加密时,如果你没有显式指定填充模式和填充…...

在本地创建repository及上传至github
文章目录 本地管理设定git的用户名与邮箱初始化添加修改提交修改设定分支问题一:error: insufficient permission for adding an object... 数据同步创建SSH keys创建并关联远程仓库上传改动至github问题二:Failed to connect to github.com port 443: Connection timed out问题…...

情人节特别定制:多种语言编写动态爱心网页(附完整代码)
写在前面案例1:HTML Three.js库案例2:HTML CSS JavaScript案例3:Python环境 Flask框架结语 写在前面 随着七夕节的临近,许多人都在寻找独特而令人难忘的方式来表达爱意。在这个数字时代,结合创意和技术࿰…...
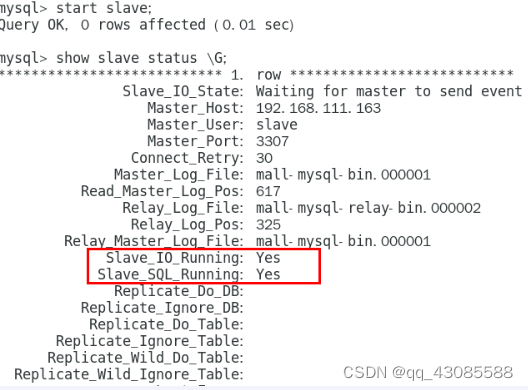
Docker mysql主从同步安装
1. 构建master实例 docker run -p 3307:3306 --name mysql-master \ -v /mydata/mysql-master/log:/var/log/mysql \ -v /mydata/mysql-master/data:/var/lib/mysql \ -v /mydata/mysql-master/conf:/etc/mysql \ -e MYSQL_ROOT_PASSWORDroot \ -d mysql:5.7 2. 构建master配置…...

docker update 命令
docker update 更新一个或多个容器的配置。官方文档 用法 $ docker update [OPTIONS] CONTAINER [CONTAINER...]请参阅选项部分OPTIONS,了解此命令可用的概述。 描述 该docker update命令动态更新容器配置。您可以使用此命令来防止容器消耗 Docker 主机的过多资…...

阻塞和挂起的区别和联系
阻塞和挂起是进程两种不同的状态,其描述如下: 阻塞:正在执行的进程由于发生某时间(如I/O请求、申请缓冲区失败等)暂时无法继续执行。此时引起进程调度,OS把处理机分配给另一个就绪进程,而让受阻…...

水力发电厂测量装置配置选型及厂用电管理系统
《水力发电厂测量装置配置设计规范》对水电厂的测量装置配置做了详细要求和指导。测量装置是水力发电厂运行监测的重要环节,水电厂的测量主要分为电气量测量和非电量测量。电气测量指使用电的方式对电气实时参数进行测量,包括电流、电压、频率、功率因数…...
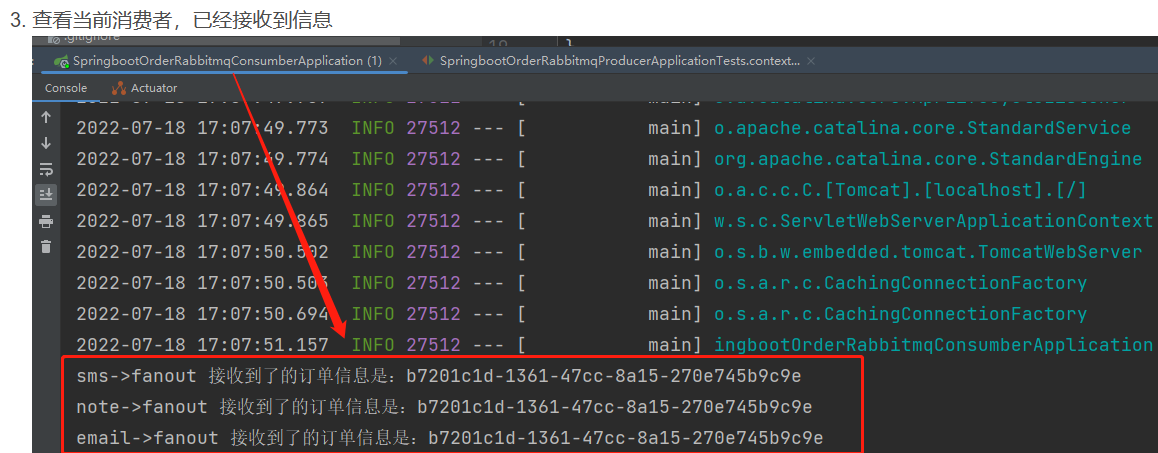
【RabbitMQ】RabbitMQ整合SpringBoot案例
文章目录 1、前情提要【RabbitMQ】2、RabbitMQ-SpringBoot案例 -fanout模式2.1 实现架构总览2.2 具体实现2.2.1生产者2.2.1消费者 1、前情提要【RabbitMQ】 【RabbitMQ】消息队列-RabbitMQ篇章 RabbitMQ实现流程 2、RabbitMQ-SpringBoot案例 -fanout模式 2.1 实现架构总览…...
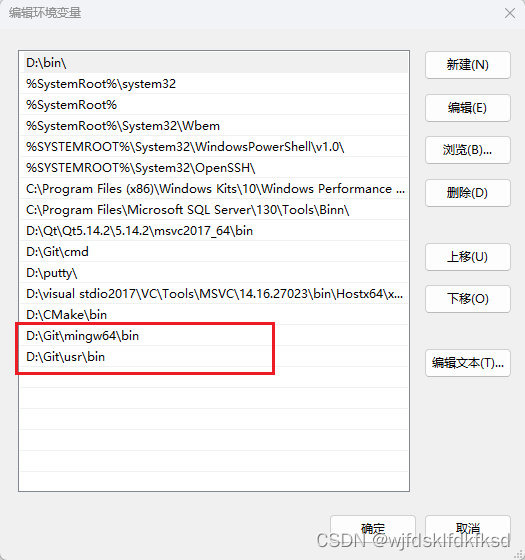
如何在window下cmd窗口执行linux指令?
1.Git:https://git-scm.com/downloads(官网地址) 2.根据自己的实际路径,添加两个环境变量 3.重启电脑...

c++基础系列:字符串、向量和数组
字符串、向量和数组 命名空间的using声明 目前用到的库函数基本上都属于命名空间std;通过using声明(using declaration)实现更简单的途径使用到命名空间中的成员。 标准库类型string string表示可变长的字符序列,必须先包含st…...
docker 05(dockerfile)
一、docker镜像原理 镜像可以复用 二、容器转镜像 将容器保存为镜像[参考] docker commit -a -m 现有容器ID 保存后的名称:版本号 -a :提交的镜像作者; -c :使用Dockerfile指令来创建镜像; -m :提交时的说明文字; -p :…...
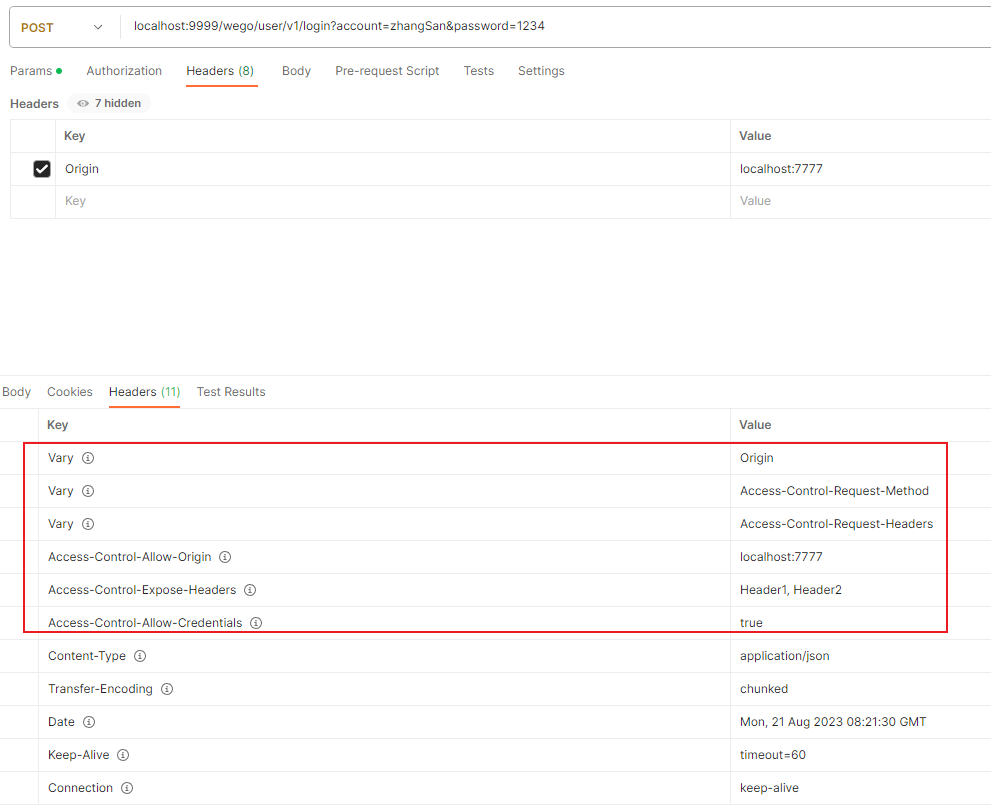
PostMan 测试项目是否支持跨域
使用PostMan可以方便快速的进行跨域测试。 只需要在请求头中手动添加一个Origin的标头,声明需要跨域跨到的域(IP:端口)就行,其余参数PostMan会自动生成。添加此标头后,请求会被做为一条跨域的请求来进行处…...
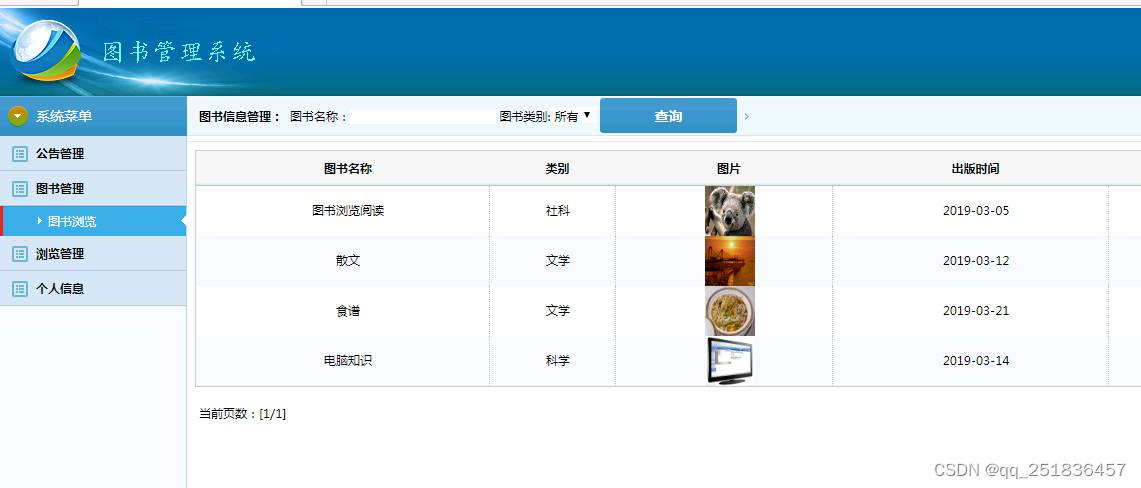
jsp 协同过滤 图书管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 JSP 协同过滤 图书管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境 为TOMCAT7.0,Myeclipse8.5开发,数据库为My…...
商城-学习整理-高级-商城业务-商品上架es(十)
目录 一、商品上架1、sku在ES中存储模型分析2、nested数据类型场景3、构造基本数据(商品上架) 二、首页1、项目介绍2、整合thymeleaf(spring-boot下模板引擎)渲染页面3、页面修改不重启服务器实时更新4、渲染二级三级数据 三、搭建…...

【水文学法总结】河道内生态流量计算方法(含MATLAB实现代码)
生态流量(Ecological Flow, EF) 是指维持河道内生态环境所需要的水流流量。生态流量计算方法众多,主要分为水文学方法、栖息地模拟法、水力学方法、整体法等,各方法多用于计算维持河道生态平衡的最小生态流量(Minimum …...
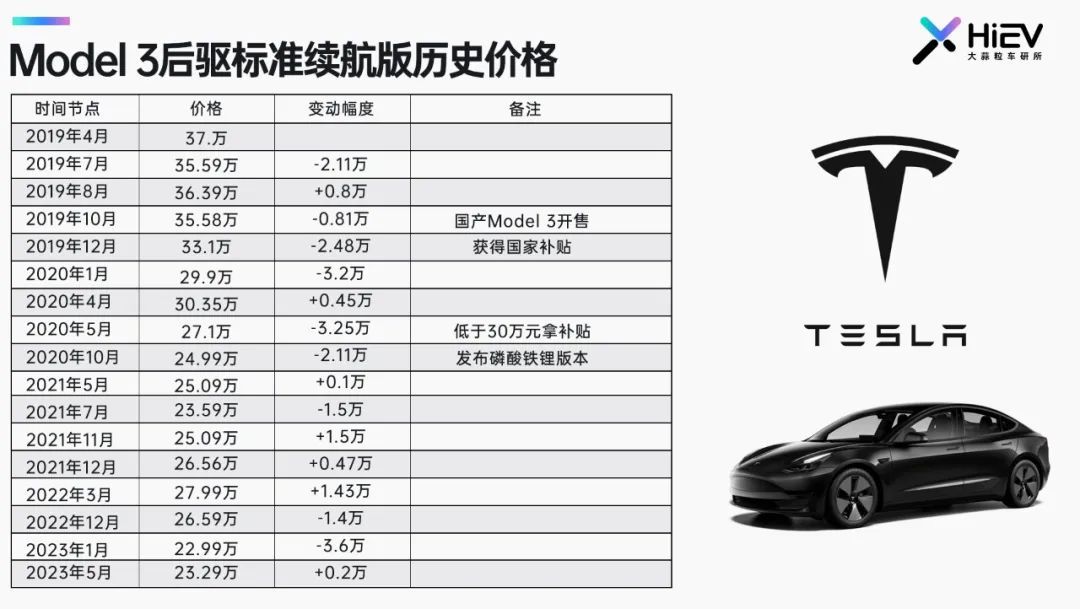
特斯拉Model 3的七年狂飙
作者 | 张祥威 编辑 | 德新 发布一周拿下32万张订单,之后用时五年,交付量突破100万辆。粗略计算,自2016年发布至今,特斯拉Model 3已交付超150万辆。 放眼新能源赛道,如此战绩 别无二家。 Model 3踩中纯电动车的…...

物流签收异常,财务对账复杂,怎么解决?
电子商务行业的蓬勃发展为人们的购物体验带来了巨大的便利,然而,随之而来的物流签收异常和财务对账复杂问题却给电商企业的财务部门带来了一系列困扰。 每天大量的订单和货物流转,不可避免地导致了物流签收数据与财务记录之间的不一致和差异…...

docker之镜像与数据卷
镜像 简介 1.镜像是一种轻量级、可执行的独立软件包,用来打包软件运行环境和基于环境开发的软件,他包含运行某个软件所需的所有内容,包括代码、运行时库、环境变量、配置文件 2.将所有的应用和环境11,直接打包成docker镜像&…...

服务器为什么会被攻击?43.248.186.x
进入信息时代,各种行业对数据的安全和技术要求也越来越高,同时也遇到了各种各样的服务器故障问题,但是网络攻击才是最大的伤害,在这上面造成了企业不必要的损失,那么服务器为什么会被攻击,这里给大家讲解一下服务器被攻击有哪几种情况 一、服…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
