胜者打仗,就像高山上决开积水,势不可挡
胜者打仗,就像高山上决开积水,势不可挡
【安志强趣讲《孙子兵法》16讲】
【原文】
是故胜兵先胜而后求战,败兵先战而后求胜。善用兵者,修道而保法,故能为胜败之政。
【注释】
修道:指从各方面修治“先立于不败”之道,如政治、经济、军事、外交等各方面条件的准备等。
【趣讲白话】
因此,胜利之师先创造出必胜的条件,然后才寻找战机与敌人交战;失败之师先要跟敌人交战,然后期望从交战中获胜。善于用兵打仗的人,总是能够准备好打仗的基础建设,平时就能保持良性运转,所以才能成为战争胜负的主宰。

【延伸一下】
工夫在平常,练好自己的内功,让自己不被敌人轻易战胜,然后等待战胜敌人的机会。
用在企业经营领域,对大多数企业而言,要从不断的积累开始,打好基础,先活下来,然后寻求突破。我有一个比喻,“要滑翔起飞,不要火箭起飞”。就是,对大多数企业来讲,不要妄想短期内获得巨大的突破。有人的经营哲学是:日积月累,滴水穿石,一以贯之,我现在倾向于这种方式。当大的机会来临时,去积极把握,这于练好内功不矛盾。
【原文】
兵法:一曰度,二曰量,三曰数,四曰称,五曰胜。地生度,度生量,量生数,数生称,称生胜。
【注释】
度,判断的意思;量,这里指容量的限度;数,数目的多少;称,权衡。
【趣讲白话】
兵法中衡量胜负的因素:一是判断国土幅员情况;二是判断军需物资情况;三是统计军队兵力;四是衡量军事综合实力;五是得出胜负的判断。国土幅员决定军需物资;军赋物资军力多寡;军力多寡决定军事实力的强弱;军事实力的不同,最终决定了战争的胜负。
【延伸一下】
孙子在当初的时代,土地、人口、物产是决定性要素。放到现在可能要把科技这个东西加上,比如以色列,科技领先,所以才能打赢中东战争。现在衡量的要素比原来要多的多,比如有个底线思维,就是要考虑最极端的情况下,怎么办?比如中国南海填岛,让中国有了“永不沉没的航母”。中国的石油70%经过马六甲海峡,包围石油运输线的安全是底线思维。
【原文】
故胜兵若以镒称铢,败兵若以铢称镒。胜者之战民也,若决积水于千仞之溪者,形也。
【注释】
镒(yì)、铢(zhū):都是古代的重量单位。镒比铢重五百多倍。
民,指士卒。
仞,古代长度单位。
【趣讲白话】
所以,胜利的军队对比失败的军队,就像用镒与铢相比较,占有绝对优势;而失败的军队对比胜利的军队,就像用铢与镒相比较,处于绝对劣势。在占优的一方,指挥士兵作战,就像决开千仞高山上的溪流积水一样,势不可当,这就是所谓的“形”。
【延伸一下】
打仗就是要构建一种局面,形成压倒性优势。
做企业也一样,要通过耐心的构建,持续不断的投入,形成压倒性优势。任正非说“我们这三十年都对着同一个‘城墙口’冲锋,几十人、几百人对着这个‘城墙口’,几万人、十几万人还是攻这个‘城墙口’,总会把这个‘城墙口’攻开的......”,就是通过持续不断的投入,在通信技术方面,构建压倒性优势。
个人也一样,通过不断积累,在能力上形成竞争优势。现在人力资源市场的情况是,高端人才,一将难求。
2023年8月19
相关文章:

胜者打仗,就像高山上决开积水,势不可挡
胜者打仗,就像高山上决开积水,势不可挡 【安志强趣讲《孙子兵法》16讲】 【原文】 是故胜兵先胜而后求战,败兵先战而后求胜。善用兵者,修道而保法,故能为胜败之政。 【注释】 修道:指从各方面修治“先立于不…...

stm32的命令规则
stm32型号的说明:以STM32F103RBT6这个型号的芯片为例,该型号的组成为7个部分,其命名规则如下:...
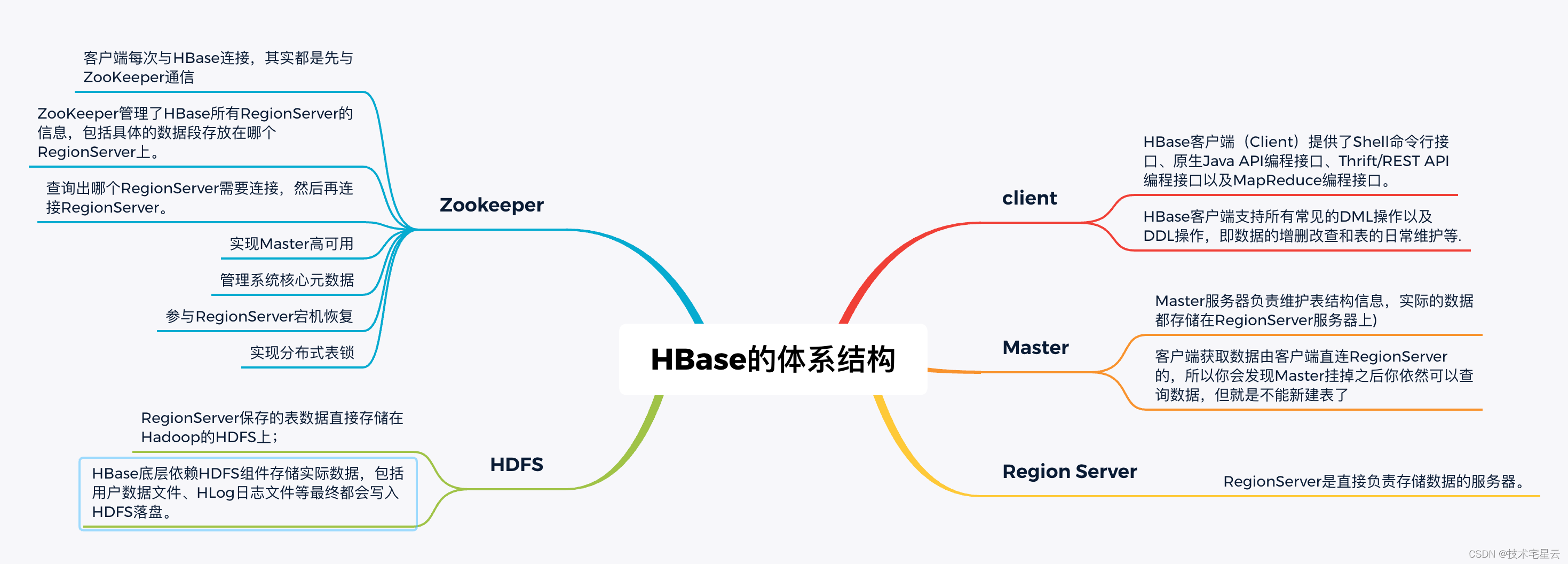
1. HBase中文学习手册之揭开Hbase的神秘面纱
揭开Hbase的神秘面纱 1.1 欢迎使用 Apache Hbase1.1.1 什么是 Hbase?1.1.2 Hbase的前世今生1.1.3 HBase的技术选型?1.1.3.1 不适合使用 HBase的场景1.1.3.2 适合使用 HBase的场景 1.1.4 HBase的特点1.1.4.1 HBase的优点1.1.4.2 HBase的缺点 1.1.5 HBase设计架构 1.…...
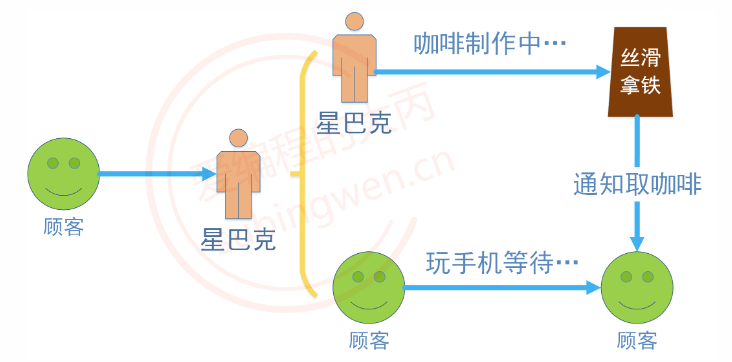
[线程/C++]线程同(异)步和原子变量
文章目录 1.线程的使用1.1 函数构造1.2 公共成员函数1.2.1 get_id()1.2.2 join()2.2.3 detach()2.2.5 joinable()2.2.6 operator 1.3 静态函数1.4 call_once 2. this_thread 命名空间2.1 get_id()2.2 sleep_for()2.3 sleep_until()2.4 yield() 3. 线程同步之互斥锁3.1 std:mute…...

全球网络加速器GA和内容分发网络CDN,哪个更适合您的组织使用?
对互联网用户来说,提供最佳的用户体验至关重要:网页加载时间过长、视频播放断断续续以及服务忽然中断等问题都足以在瞬间失去客户。因此可以帮助提高您的网站或APP提高加载性能的解决方案就至关重要:全球网络加速器和CDN就是其中的两种解决方…...
蓝凌OA custom.jsp 任意文件读取
曾子曰:“慎终追远,民德归厚矣。” 漏洞复现 访问漏洞url: 出现漏洞的文件为 custom.jsp,构造payload: /sys/ui/extend/varkind/custom.jsp var{"body":{"file":"file:///etc/passwd&q…...
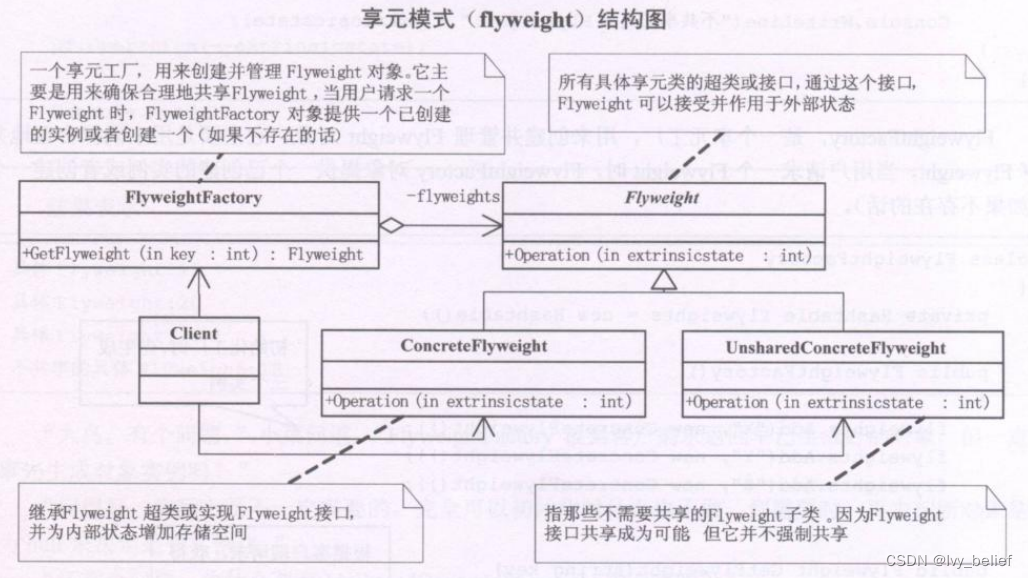
(二)结构型模式:7、享元模式(Flyweight Pattern)(C++实例)
目录 1、享元模式(Flyweight Pattern)含义 2、享元模式的UML图学习 3、享元模式的应用场景 4、享元模式的优缺点 5、C实现享元模式的简单实例 1、享元模式(Flyweight Pattern)含义 享元模式(Flyweight)…...

laravel 多次查询请求,下次请求清除上次请求的where 条件
在Laravel中,可以使用where方法来添加查询条件,但是每次添加where条件时,都会在查询构造器中持久化这些条件,直到你手动重置它们。所以,如果你想在下一次查询中清除上次查询的where条件,有以下几种选择&…...

C++根据如下使用类MyDate的程序,写出类MyDate的定义,MyDate中有三个数据成员:年year,月month,日day完成以下要求
题目: 根据如下使用类MyDate的程序,写出类MyDate的定义,MyDate中有三个数据成员: 年year,月month,日day int year,month,day; void main() { MyDate d1, d2; d1.set(2015, 12, 31); d2.set(d1); d1.…...
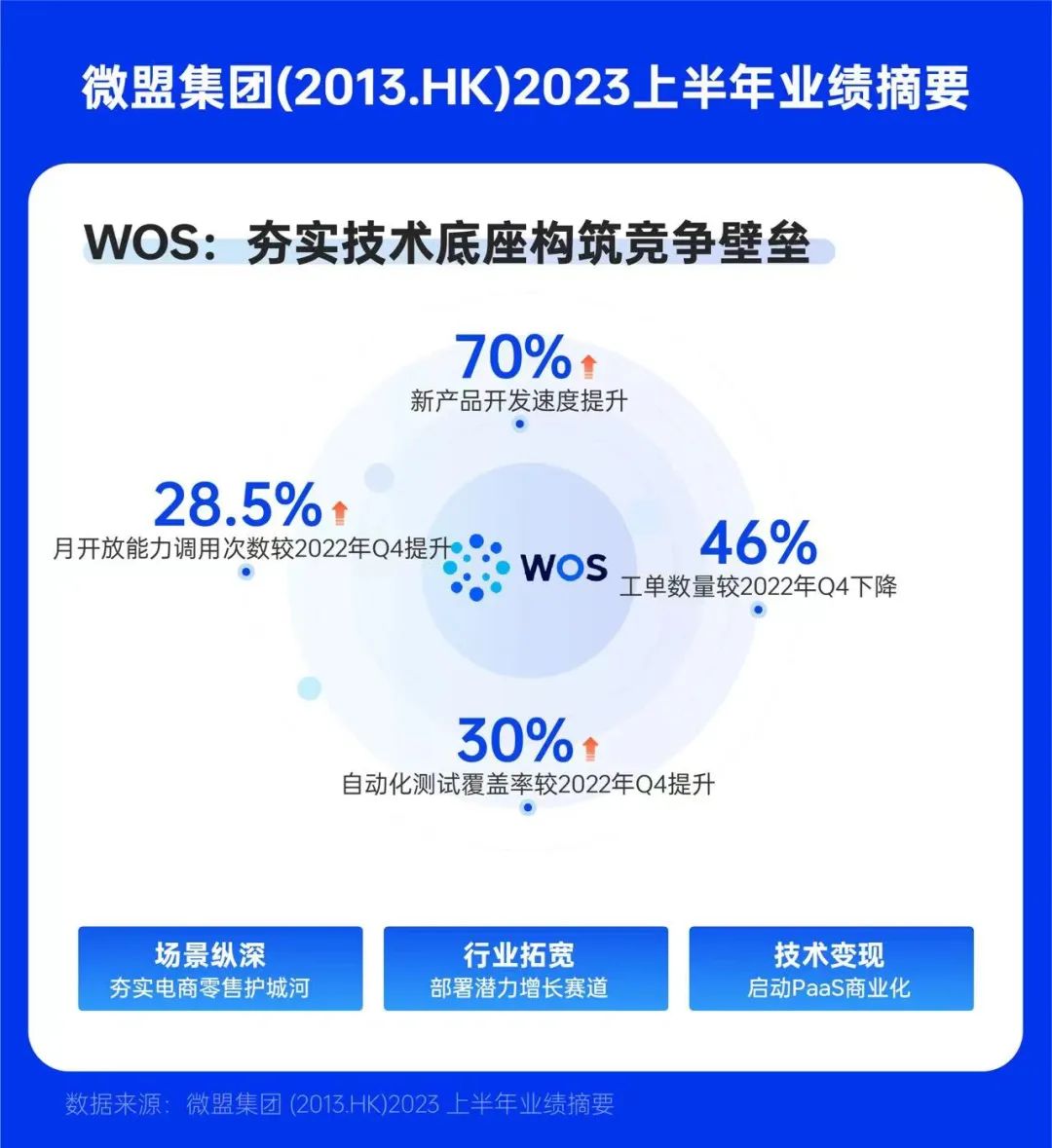
微盟集团中报增长稳健 重点发力智慧零售AI赛道
零售数字化进程已从渠道构建走向了用户的深度运营。粗放式用户运营体系无法适应“基于用户增长所需配套的精细化运营能力”,所以需要有个体、群体、个性化、自动化运营——即在对的时候、以对的方式、把对的内容推给用户。 出品|产业家 2023年已经过半,经济复苏成为…...
模板方法模式)
设计模式(7)模板方法模式
一、定义: 定义一个操作中的算法骨架,而将算法的一些步骤延迟到子类中,使得子类可以不改变该算法结构的情况下重定义该算法的某些特定步骤。它是一种类行为型模式。 //模板方法抽象类 public abstract class AbstractClass {//模板方法publ…...

2308C++协程流程9
参考 #include <协程> #include "简异中.cpp" //用来中文定义的.元<类 T>构 P;元<类 T>构 任务{用 承诺型P<T>;任务()默认;动 符号 协待()常 无异{构 等待器{极 直接协()常 无异{中 p.是准备好();}协柄 挂起协(协柄<>o)常 无异{p.连续…...

基于学习交流社区的自动化测试实现
一 项目介绍 项目名称 项目名称: 学习交流社区 项目介绍 项目介绍: 学习交流社区是一个基于Spring的前后端分离的在线论坛系统。使用了MySQL数据库来存储相关信息,项目完成后使用Xshell将其部署到云服务器上。 前端页面: 前端共由…...

2023-08-21力扣每日一题
链接: 2337. 移动片段得到字符串 题意: L可以和左边的_交换,R可以和右边的_交换,求判断A是否能通过交换(不限次数)变成B 解: 观察可知,如果存在RL,一定不能交换出LR,…...

对象存储服务-MinIO基本集成
是什么 MinIO 是一个高性能的分布式对象存储服务,适合存储非结构化数据,如图片,音频,视频,日志等。对象文件最大可以达到5TB。 安装启动 mkdir -p /usr/local/minio cd /usr/local/minio# 下载安装包 wget https:/…...

Yarn介绍及快速安装 - Debian/Ubuntu Linux
1.Yarn介绍 Yarn 是一个用于管理 JavaScript 包的快速、可靠和安全的包管理器。它是由 Facebook、Google、Exponent 和 Tilde 团队共同开发的,旨在提供比 npm 更快速、可靠的包管理体验。 以下是 Yarn 的一些主要特点和优势: 快速安装:Yarn…...
】第10課 中国の生活に慣れるかどうか少し心配です)
【新日语(2)】第10課 中国の生活に慣れるかどうか少し心配です
第10課 中国の生活に慣れるかどうか少し心配です 注释: ~かどうか:“是否”。 练习A 一、例句 田中さんは鈴木さんに、30分ぐらい遅れると言いました。 田中先生告诉铃木先生,他会迟到大约30分钟。 注释: &…...

Python 网页解析初级篇:BeautifulSoup库的入门使用
在Python的网络爬虫中,网页解析是一项重要的技术。而在众多的网页解析库中,BeautifulSoup库凭借其简单易用而广受欢迎。在本篇文章中,我们将学习BeautifulSoup库的基本用法。 一、BeautifulSoup的安装与基本使用 首先,我们需要使…...

Spring Schedular 定时任务
大家好 , 我是苏麟 , 今天带来定时任务的实现 . Spring网站 : 入门 |计划任务 (spring.io) 什么是定时任务 通过时间表达式来进行调度和执行的一类任务被称为定时任务 定时任务实现 1.Spring Schedule (Spring boot 默认整合了) 2.Quartz(独立于Spring 存在的定时任务框架…...

营业额统计
营业额统计 # 题目描述 Tiger 最近被公司升任为营业部经理,他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。 Tiger 拿出了公司的账本,账本上记录了公司成立以来每天的营业额。分析营业情况是一项相当复杂的工作。由于节假日&…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
