5.8 汇编语言:汇编高效除法运算
通常情况下计算除法会使用div/idiv这两条指令,该指令分别用于计算无符号和有符号除法运算,但除法运算所需要耗费的时间非常多,大概需要比乘法运算多消耗10倍的CPU时钟,在Debug模式下,除法运算不会被优化,但Release模式下,除法运算指令会被特定的算法经过优化后转化为为乘法,这样就可以提高除法运算的效率。
- 1.如果被除数是一个未知数,那么编译器无法确定数值,则编译器会使用原始的
div指令计算,程序的执行效率会变低。 - 2.如果除数是2的次幂,那么可以将其转化为处理速度快的
shr逻辑右移指令指令,该指令的执行只需要1个时钟周期,效率最高。 - 3.如果要进行2的次幂,并且该数是有符号数,则只需要使用
sar算数右移指令,即可进行快速除法运算。
8.1 使用IDIV指令完成除法
与乘法运算相同,在不考虑效率前提下,完全可以使用IDIV指令完成除法运算,该指令比乘法还慢。
- 计算除法时应遵循:
- 如果除数为
8位被除数为16位,则结果的商存放在AL中,余数存放AH中 - 如果除数为
16位被除数为32位,则结果的商存放与AX中,余数存放DX中 - 如果除数为
32位被除数为64位,则结果的商存放与EAX中,余数存放EDX中 - 指令
CDQ用于扩展寄存器,扩展后EDX存储高位而EAX存储低位
除法指令计算很简单,只需要扩展CDQ寄存器,然后累计除即可。
.datax DWORD ?y DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],1000mov dword ptr ds:[y],20; 计算 x / ymov eax,dword ptr ds:[x] ; eax = 1000cdq ; 把eax的第31bit复制到edx的每个bit上idiv dword ptr ds:[y] ; eax = x / yinvoke crt_printf,addr szFmt,eaxmain ENDP
END main
8.2 除数为正2的次幂(无符号)
如果除数是正数被除数也是正数,且除数的范围是正2的次幂,那么我们就可以使用sar算数右移指令来替代div除法指令,通过改变2的次幂的移位次数即可实现无符号除法的高速运算。
- 计算时我们需要参考次方表,这里我列举出几个常用的次方数值:
- 次方表: 1=>2 2=>4 3=>8 4=>16 5=>32 6=>64 7=>128
- 次方表: 8=>256 9=>512 10=>1024 11=>2048 12=>4096 13=>8192 14=>16384
以下代码中分别演示了除数为2/4/8三种计算方式,计算结果只需sar移位即可实现。
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],5; ----------------------------------------------------; 【除数为2】; 被除数为正数(无需扩展): eax => 5 / 2 = 2mov eax,dword ptr ds:[x] ; 被除数sar eax,1 ; 算数右移1位invoke crt_printf,addr szFmt,eax; ----------------------------------------------------; 【除数为4】; 被除数为正数(无需扩展): eax => 5 / 4 = 1mov eax,dword ptr ds:[x]sar eax,2 ; 算数右移2位invoke crt_printf,addr szFmt,eax; ----------------------------------------------------; 【除数为8】; 被除数为正数(无需扩展): eax => 5 / 8 = 0mov eax,dword ptr ds:[x]sar eax,3 ; 算数右移3位invoke crt_printf,addr szFmt,eaxinvoke ExitProcess,0main ENDP
END main
8.3 除数为负2的次幂(有符号)
如果除数是负数,且除数范围在负2的次幂内,那么在计算时应使用cdq指令将被除数EAX扩展为64位,并将扩展后的结果放入EDX:EAX寄存器内,然后使用sub eax,edx减去高位符号位,接着通过sar算数右移指令完成除法运算,最终通过neg指令将结果翻转即可。
- 总结计算过程如下:
- 1.使用
cdq指令将eax扩展为64位,结果分别存入EDX:EAX寄存器内. - 2.使用
sub eax,edx指令将高位符号位通过减法减掉. - 3.使用
sar eax,x指令完成算数右移除法运算. - 4.使用
neg eax将计算后的正数反转为负数.
这个过程通过汇编语言实现代码很简单,如下代码演示了除数为正数且被除数为 -2/-4/-8 次幂的计算过程.
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],10; 除数为(有符号)负2的次幂的计算过程; 计算 10 / -2mov eax,dword ptr ds:[x] ; x = 10cdq ; 符号扩展 [edx:eax]sub eax,edx ; 减去符号位sar eax,1 ; eax = 10 / -2neg eax ; 将正数 eax 翻转为负数 = -5invoke crt_printf,addr szFmt,eax; 计算 10 / -4mov eax,dword ptr ds:[x] ; x = 10cdqand edx,3add eax,edxsar eax,2 ; eax = 10 / -4neg eax ; eax = -2invoke crt_printf,addr szFmt,eax; 计算 10 / -8mov eax,dword ptr ds:[x]cdqand edx,7add eax,edxsar eax,3neg eaxinvoke crt_printf,addr szFmt,eaxinvoke ExitProcess,0main ENDP
END main
8.4 被除数为负数(有符号)
在有符号数的除法中,如果被除数为负数,而除数是正2的次幂,那么可以使用neg取反操作来得到正确的计算结果。具体步骤如下:
- 首先,将被除数的绝对值与除数进行除法运算,并得到正确的商。
- 如果被除数为负数,则对商进行取反操作。
- 如果除数为负数,则最终结果也要进行取反操作。
例如,假设要计算-27除以8的值,我们可以按照如下步骤进行计算:
- 计算27除以8的值,得到商3和余数3。
- 因为被除数为负数,所以对商取反,得到-3。
- 因为除数为正数,所以最终结果为-3,即-27/8的计算结果。
类似地,如果除数为负数,我们需要在得到正确的计算结果后再进行一次取反操作,这样才能得到真正的结果。需要注意的是,上述方法仅适用于除数为正2的次幂的情况下。对于其他情况,需要使用更为复杂的算法来完成除法计算。
.datax DWORD ?y DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],-10mov dword ptr ds:[y],-5; 被除数为(有符号)的计算过程; 计算 -10 / 2mov eax,dword ptr ds:[x]cdqsub eax,edxsar eax,1 ; eax = -10 / 2invoke crt_printf,addr szFmt,eax; 计算 -5 / 4mov eax,dword ptr ds:[y]cdqxor edx,edxadd eax,edxsar eax,2 ; eax = -5 / 4invoke crt_printf,addr szFmt,eax; 计算 -10 / 8mov eax,dword ptr ds:[x]cdq ; 位扩展xor edx,edx ; 清空高位add eax,edxsar eax,3 ; eax = -10 / 8invoke crt_printf,addr szFmt,eaxinvoke ExitProcess,0main ENDP
END main
8.5 除数与被除数均为负数(有符号)
在有符号数的除法中,如果除数和被除数均为负数,且除数为负2的次幂,可以使用算数右移指令sar来完成除法运算,然后通过取反指令neg来翻转得到的计算结果的符号位。
具体来说,一个有符号整数除以负2的次幂,等价于这个有符号整数右移除数的位数作为移位数,然后转为无符号数进行运算,再将得到的无符号数转回符号位正确的有符号数即可。由于右移的操作是算数右移,所以被移位的符号位会被保留。
例如,将-16除以-8,即计算-16/-8的结果,因为8是2的3次幂,所以我们可以通过算数右移指令来完成除法,然后再取反获得正确的结果:
- 将-16右移3位,得到-2。
- 对-2进行取反,得到2。
因为-16和-8均为负数,所以最终结果也要进行一次取反操作。因此,得到的结果为-2。
需要注意的是,上述方法仅适用于除数为负2的次幂,如果除数不是负2的次幂,则需要使用其他算法来计算除法运算。
.datax DWORD ?y DWORD ?z DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],-5mov dword ptr ds:[y],-24mov dword ptr ds:[z],-10; 如果同时为负数的情况; 计算 -5 / -2mov eax,dword ptr ds:[x]cdq ; 符号扩展xor edx,edx ; 清空高位add eax,edxsar eax,1 ; 算数右移动 -5 / -2neg eax ; eax = 3 (负负得正)invoke crt_printf,addr szFmt,eax; 计算 -24 / -4mov eax,dword ptr ds:[y]cdq ; 符号扩展xor edx,edx ; 清空高位add eax,edxsar eax,2 ; 算数右移动 -24 / -4neg eax ; eax = 6 (负负得正)invoke crt_printf,addr szFmt,eax; 计算 -10 / -8mov eax,dword ptr ds:[z] ; z = -10 cdq ; 符号扩展xor edx,edx ; 清空高位add eax,edxsar eax,3 ; eax = -10 / -8 neg eax ; eax = 1 (负负得正)invoke crt_printf,addr szFmt,eaxinvoke ExitProcess,0main ENDP
END main
如上我们所有的除法运算中,无论是有符号还是无符号都在进行2的次幂运算,通常针对2的次幂运算并不需要经过特殊的模M计算,而对于非2次幂3/5/7的运算,则需要通过一定的公式才能简化计算过程,如下将开始介绍非2次幂除法运算该如何优化。
8.6 除数为正非2次幂(有符号)
对于除数为正非2次幂的有符号数,我们需要使用其他的算法来完成除法运算。通常情况下,可以使用恒等式转化法或移位除法来进行计算。
一种常用的移位除法算法是:
- 将被除数与除数分别取绝对值,并记录下符号。
- 如果除数大于被除数,则直接返回0。
- 通过不断将除数左移,直到左移之后的除数大于等于被除数,得到最高位的不为0的位数,记为n。
- 将除数左移n位,然后不断依次将左移后的除数与被除数相减,直到被除数小于除数。
- 记录下相减的次数,即为最终的商。
上述算法仅适用于除数为正数的情况。如果除数为负数,则需要先取反,然后使用移位除法的算法来计算除法运算,并最终再取反,以得到正确的计算结果。
关于求解公式2^(32+n) / M的使用方法:可以通过移位和除法结合的方法来计算,具体可以按照以下步骤进行计算:
- 将除数M保存在寄存器中,将
32+n的值保存在寄存器中。 - 执行左移指令,将
32+n左移至最高位。将左移后的值保存在另一个寄存器中。 - 执行除法指令,将左移后的值除以M,得到商和余数。
- 如果余数不为0,则重新计算
32+n+1的值,再次执行上述步骤。
这样,不断重复这个过程,就可以计算出2^(32+n) / M的结果。
先来看一段汇编代码,我们此时已知 M = 055555556h 且 edx = N 带入公式 2^(32+N) / M 由于edx没有变化所以此处应计算 2^32 / 055555556h = 2.9999 即可计算出此处的除数是3,而被除数则是ecx寄存器内的值,我们即可得知该段汇编指令在进行 ecx / 3 的计算流程。
mov ecx,dword ptr ds:[y] ; 被除数
mov eax,055555556h ; M值 => 此处的M模值是编译器计算后得到的(我们无需深入理解)
imul ecx
mov eax,edx ; edx = N
shr eax,01fh
add edx,eax
invoke crt_printf,addr szFmt,edx
再来看另一段,这段代码中 sar edx,1 此时edx的值发生过一次变化变换了1次,所以公式中应该加上变化的一次计算得到 2^33 / 66666667 = 5 所以可得到当前除数是5
mov ecx,dword ptr ds:[y] ; ecx = 10 / 5 = 2
mov eax,066666667h ; 此处的M模值是编译器计算后得到的
imul ecx
sar edx,1 ; 想要知道除数是多少,只需要执行以下计算
mov eax,edx ; 2^(32 + edx) / M = 2^33 / 66666667 = 5
shr eax,01fh ; 33次方的由来,其实是默认的32次方加上 sar edx,1 中的1次方得到的
add edx,eax
invoke crt_printf,addr szFmt,edx
针对除数为非2的次幂且为有符号数,只需要提供对应的M模值,根据模值即可将对应的除法转换为乘法,一般写法如下:
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],10; 除法(无符号)非2的幂转换为乘法; 计算 10 / 3mov ecx,dword ptr ds:[x] ; 被除数 ecx = 10 / 3 = 3mov eax,055555556h ; eax = M值 1431655766imul ecxmov eax,edx ; edx = n 计算: 2^(32+n) / Mshr eax,01fh ; 计算出除数为 2.9999 => 3add edx,eaxinvoke crt_printf,addr szFmt,edx; 计算 10 / 5mov ecx,dword ptr ds:[x] ; ecx = 10 / 5 = 2mov eax,066666667h ; 此处的M模值是编译器计算后得到的imul ecxsar edx,1 ; 想要知道除数是多少,只需要mov eax,edx ; 2^(32 + edx) / M = 2^33 / 66666667 = 5shr eax,01fh ; 逻辑右移add edx,eaxinvoke crt_printf,addr szFmt,edx; 计算 10 / 6mov ecx,dword ptr ds:[x] ; ecx = 10 / 6 = 1mov eax,02AAAAAABh ; eax = 715827883imul ecxmov eax,edx ; 2^(32 + edx) / M = 2^32 / 2AAAAAAB = 6shr eax,01fhadd edx,eaxinvoke crt_printf,addr szFmt,edxinvoke ExitProcess,0main ENDP
END main
8.7 除数为正非2次幂(无符号)
在上方代码中的除法计算是针对有符号数进行的,如果是针对无符号数则需要另一种计算方式,对于除数为正非2次幂的无符号数,这里介绍一种常用的算法,恒等式转化法。
假设我们需要计算一个64位无符号整数x除以一个32位无符号整数y的值,我们可以按照以下步骤进行计算:
- 计算
2^32/y的低32位,假设得到的结果为k,即k = floor(2^32/y)。 - 将x的高32位和低32位分别除以y,并将商的高32位保存下来,记为q1,即
q1 = floor(high_32_bits(x) / y)。 - 将q1乘以k,并将结果右移32位,得到
kq1的高32位,记为q2,即q2 = floor( k * q1 / 2^32 )。 - 将x的低32位与被除数的乘积减去 q2 乘以y的值就是x除以y的值,即
(floor(x * k / 2^32) - q2) * y + x mod y。
以上步骤可以用以下公式来表示:
x / y = [(floor(high_32_bits(x) / y) * floor(2^32 / y) + floor(k * floor(high_32_bits(x) / y) / 2^32) * 2^32) * y + x mod y] / y
其中,high_32_bits(x)表示x的高32位,floor()表示向下取整,mod表示取余数。
需要注意,上述算法仅适用于除数为正数的情况。如果除数为负数,则需要先将除数取反,然后使用恒等式转化法的算法来计算除法运算,并最终再取反,以得到正确的计算结果。
.datax DWORD ?y DWORD ?z DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],-5mov dword ptr ds:[y],10mov dword ptr ds:[z],20; 除法(无符号)非2的次幂(正数)转换为乘法xor edx,edxmov ecx,dword ptr ds:[y] ; ecx = 10mov eax,0AAAAAAABh ; ecx / 3 = 3mul ecxshr edx,1invoke crt_printf,addr szFmt,edx; 还原除数: 2 ^(32 + n) / M => 2 ^ (32+2) / 0CCCCCCCDh = 5xor edx,edxmov ecx,dword ptr ds:[y] ; ecx = 10 => 计算: 10/5mov eax,0CCCCCCCDh ; eax = Mmul ecxshr edx,2 ; edx= ninvoke crt_printf,addr szFmt,edx; 还原除数: 2 ^(32 + n) / M => 2 ^ (32+2) / 0AAAAAAABh = 6xor edx,edxmov ecx,dword ptr ds:[y] ; ecx = 10 => 计算:10/6mov eax,0AAAAAAABh ; eax = Mmul ecxshr edx,2 ; edx = ninvoke crt_printf,addr szFmt,edx;还原除数: 2 ^(32 + n) / M => 2 ^ 33 / 038E38E39h = 9xor edx,edxmov ecx,dword ptr ds:[z] ; ecx = 20 => 计算: 20/9mov eax,038E38E39h ; eax = Mmul ecxshr edx,1 ; edx = ninvoke crt_printf,addr szFmt,edxinvoke ExitProcess,0main ENDP
END main
8.8 除数为负非2次幂(无符号)
如果我们的除数是一个负数,且范围是非2的次幂,那么当我们计算结束后,只需要在原来基础上多增加一个neg将结果翻转以下即可。
采用与有符号整数的移位除法类似的方法,分为两个阶段完成。
- 阶段1:将除数和被除数分别取绝对值,并计算出商的符号。由于除数为负数,所以商的符号为负号。
- 阶段2:使用移位除法算法(详见上述有符号数除法的算法),计算出无符号整数的商。
最后,因为商为负数,所以需要将其翻转一下,即执行一次取反指令neg,以得到正确的计算结果。
.datax DWORD ?y DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],10mov dword ptr ds:[y],20; 还原除数: 2 ^(32 + n) / M => 2 ^ 33 / 0AAAAAAABh = nge(3) => -3xor edx,edxmov ecx,dword ptr ds:[y] ; ecx = 20 => 计算: 20 / -3mov eax,0AAAAAAABh ; eax = Mmul ecxshr edx,1 ; edx = n neg edx ; edx=6 结果neg取反invoke crt_printf,addr szFmt,edx; 还原除数: 2 ^(32 + n) / M => 2 ^ 62 / 040000001h = 4294967292xor edx,edxmov ecx,dword ptr ds:[x] ; ecx = 10 => 计算: 10 / -3mov eax,040000001h ; eax = Mmul ecxshr edx,01eh ; edx = ninvoke crt_printf,addr szFmt,edxinvoke ExitProcess,0main ENDP
END main
而如果反过来,被除数变成负数,而除数则还是非2的次幂,那么计算方式应该如下所示:
.datax DWORD ?szFmt BYTE '计算结果: %d',0dh,0ah,0
.codemain PROCmov dword ptr ds:[x],-10; 除法(有符号)非2的幂转换为乘法mov ecx,dword ptr ds:[x] ; ecx = -10 / 9 = -1mov eax,038E38E39h ; eax = 954437177 imul ecxsar edx,1 ; 2^(32 + edx) / M = 2^33 / 38E38E39 = 9mov ecx,edxshr ecx,01fhadd edx,ecxinvoke crt_printf,addr szFmt,edxinvoke ExitProcess,0main ENDP
END main
本文作者: 王瑞
本文链接: https://www.lyshark.com/post/1f99ad3b.html
版权声明: 本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
相关文章:

5.8 汇编语言:汇编高效除法运算
通常情况下计算除法会使用div/idiv这两条指令,该指令分别用于计算无符号和有符号除法运算,但除法运算所需要耗费的时间非常多,大概需要比乘法运算多消耗10倍的CPU时钟,在Debug模式下,除法运算不会被优化,但…...

如何通过python来给手机发送一条短信?
要通过Python发送短信到手机,您可以使用不同的短信服务提供商的API。以下是一个使用Twilio和Sinch服务提供商的示例,您可以根据自己的选择来决定使用哪个。 使用Twilio发送短信: 首先,注册一个Twilio账户并获取您的账户SID、认证令牌和Twilio号码。 安装 twilio 包,如果您…...

无涯教程-PHP - IntlChar类
在PHP7中,添加了一个新的 IntlChar 类,该类试图公开其他ICU函数。此类定义了许多静态方法和常量,可用于操作unicode字符。使用此类之前,您需要先安装 Intl 扩展名。 <?phpprintf(%x, IntlChar::CODEPOINT_MAX);print (IntlCh…...

【Linux操作系统】Linux系统编程中信号捕捉的实现
在Linux系统编程中,信号是一种重要的机制,用于实现进程间通信和控制。当某个事件发生时,如用户按下CtrlC键,操作系统会向进程发送一个信号,进程可以捕获并相应地处理该信号。本篇博客将介绍信号的分类、捕获与处理方式…...

【PHP】基础语法变量常量
文章目录 PHP简介前置知识了解静态网站的特点动态网站特点 PHP基础语法代码标记注释语句分隔(结束)符变量变量的基本概念变量的使用变量命名规则预定义变量可变变量变量传值内存分区 常量基本概念常量定义形式命名规则使用形式系统常量魔术常量 PHP简介 PHP定义:一…...

Failed to resolve: com.github.mcxtzhang:SwipeDelMenuLayout:V1.3.0
在allprojects下的repositories闭包里面添加jcenter()和maven {url https://jitpack.io},具体可以看你的第三方框架需要添加什么仓库,大多数都只需要上面两个。 我的build.gradle(Project)完整内容如下: buildscript …...

常用 Python IDE 汇总(非常详细)从零基础入门到精通,看完这一篇就够了
写 Python 代码最好的方式莫过于使用集成开发环境(IDE)了。它们不仅能使你的工作更加简单、更具逻辑性,还能够提升编程体验和效率。 每个人都知道这一点。而问题在于,如何从众多选项中选择最好的 Python 开发环境。初级开发者往往…...

【Hive】HQL Map 『CRUD | 相关函数』
文章目录 1. Map 增删改查1.1 声明 Map 数据类型1.2 增1.3 删1.4 改1.5 查 2. Map 相关函数2.1 单个Map 3. Map 与 String3.1 Map 转 string3.2 string 转 Map 1. Map 增删改查 1.1 声明 Map 数据类型 语法:map<基本数据类型, 基本数据类型> 注意是<>…...

ELF修复基本工作原理
ELF修复基本工作原理 ELF(Executable and Linkable Format)是一种常见的可执行文件和可链接文件的格式,广泛用于Linux和UNIX系统中。ELF修复是指对ELF文件进行修改或修复,以确保其正确加载和执行。 ELF修复的基本工作原理如下: 识别ELF文件:首先,需要识别和验证目标文…...
matlab实现输出的几种方式(disp函数、fprintf函数、print函数)
matlab实现输出的几种方式(disp函数、fprintf函数、print函数) 输出为文本、文件、打印 1、disp函数 显示变量的值,如果变量包含空数组,则会返回 disp,但不显示任何内容。 矩阵 A [1 0]; disp(A)结果 字符串 S …...

C/C++数据库编程
文章目录 0. Mysql安装与开发环境配置1. win10 Navicat 连接虚拟机的MySQL需要关闭防火墙2. 由于找不到libmysql.dIl, 无法继续执行代码。重新安装程序可能会解决此问题。3. 测试连接数据库,并插入数据4. C封装MySQL增删改查操作 0. Mysql安装与开发环境配置 MySQL…...
通过python在unity里调用C#接口
log: 背景 最近在做虚拟人底层驱动sdk测试,因为后端使用的是C#,我个人更倾向于python编程辅助测试工作,测试sdk需要通过开发提供的接口方法文档,通过传测试场景参数调用方法进行单元测试 技术&工具 项目语言 C# 项目工具 unity 测试…...
C++笔记之左值与右值、右值引用
C笔记之左值与右值、右值引用 code review! 文章目录 C笔记之左值与右值、右值引用1.左值与右值2.右值引用——关于int&& r 10;3.右值引用——对比int&& r 10;和int& r 10;4.右值引用(rvalue reference)的概念 1.左值与右值 2.…...
JS逆向-某招聘平台token
前言 本文是该专栏的第56篇,后面会持续分享python爬虫干货知识,记得关注。 通常情况下,JS调试相对方便,只需要chrome或者一些抓包工具,扩展插件,就可以顺利完成逆向分析。目前加密参数的常用逆向方式大致可分为以下几种,一种是根据源码的生成逻辑还原加密代码,一种是补…...
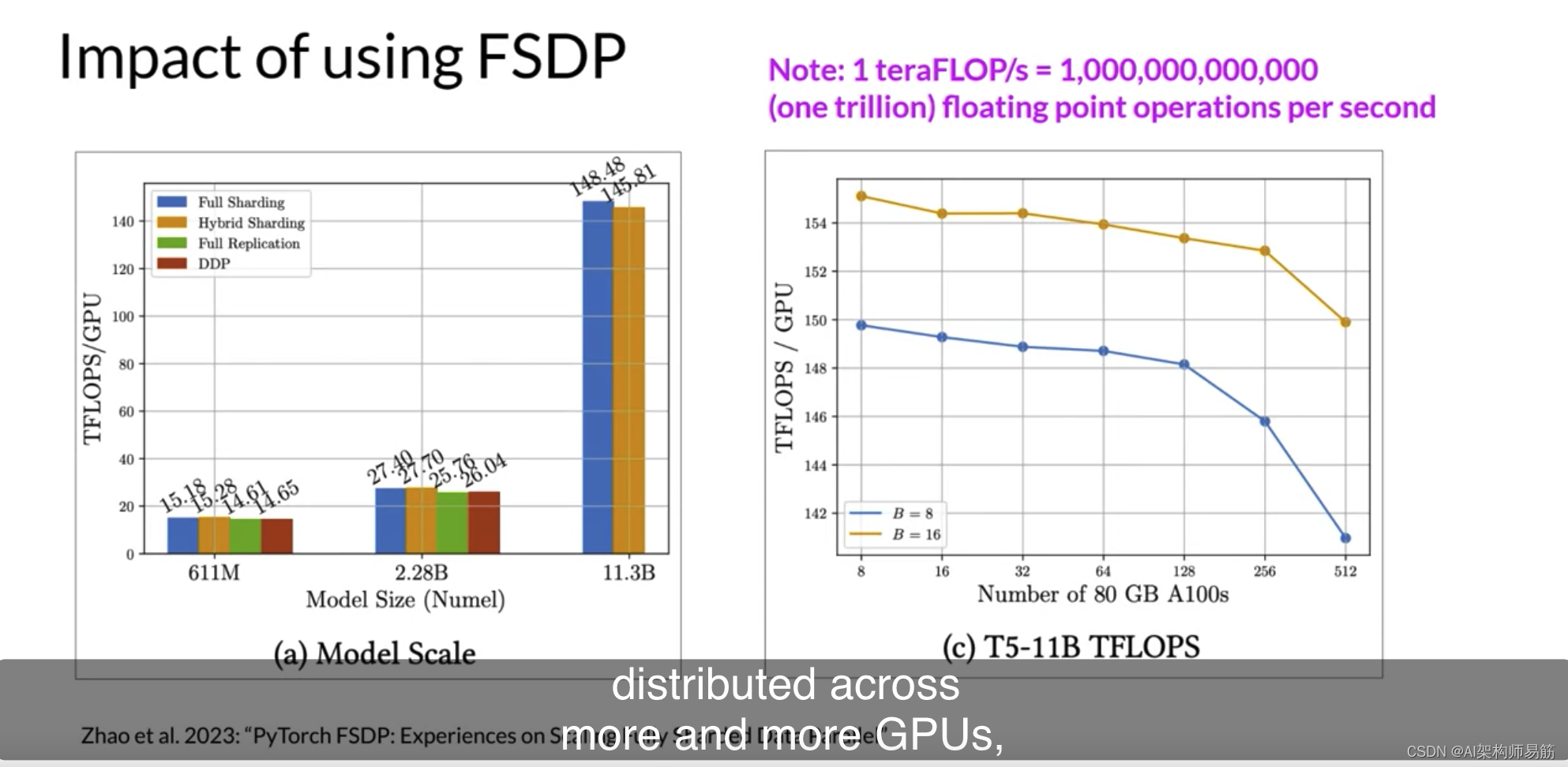
LLMs高效的多 GPU 计算策略Efficient multi-GPU compute strategies
很有可能在某个时候,您需要将模型训练工作扩展到超过一个GPU。在上一个视频中,我强调了当您的模型变得太大而无法适应单个GPU时,您需要使用多GPU计算策略。但即使您的模型确实适合单个GPU,使用多个GPU加速训练也有好处。即使您正在…...
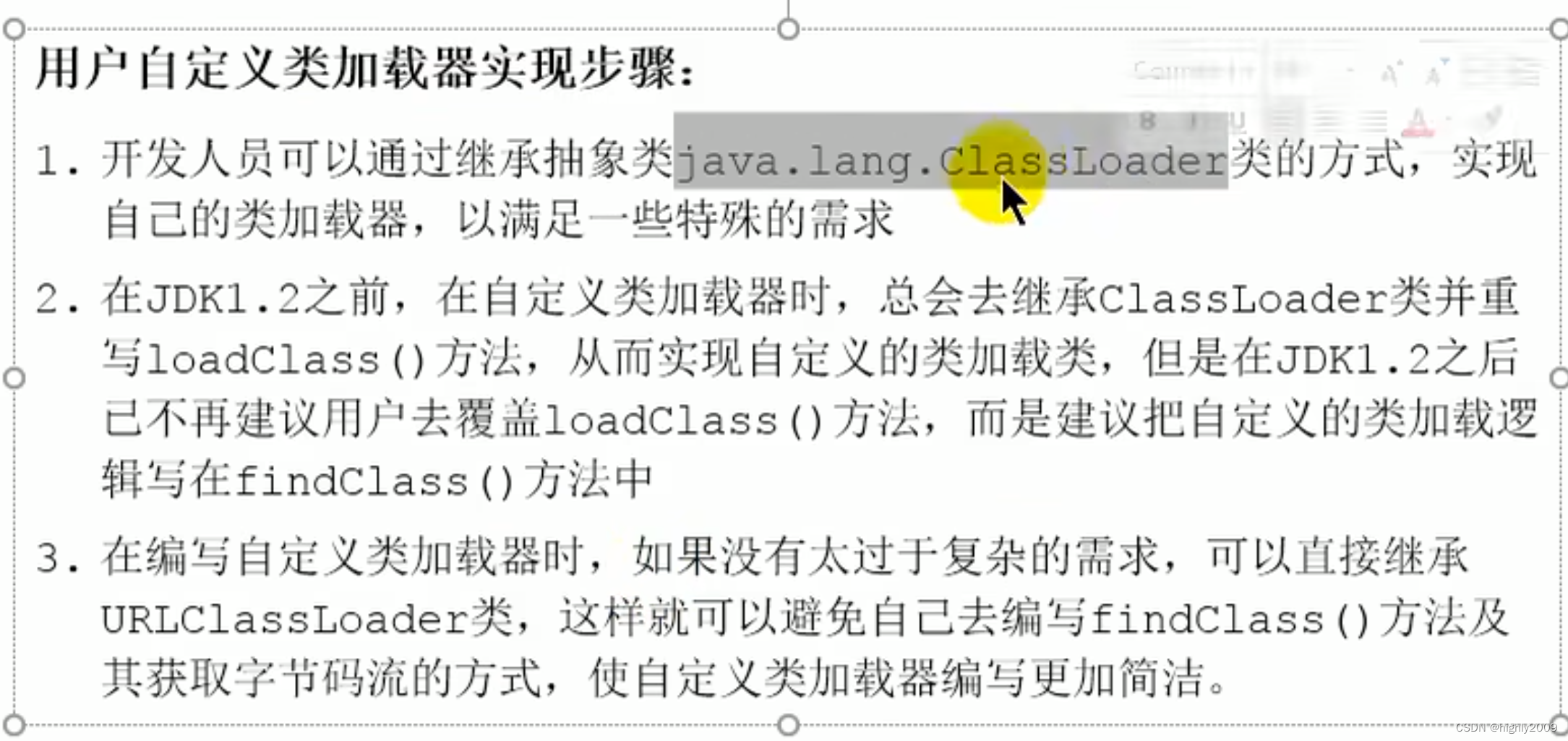
jvm-类加载子系统
1.内存结构概述 类加载子系统负责从文件系统或网络中加载class文件,class文件在文件开头有特定的文件标识 ClassLoader只负责class文件的加载,至于它是否运行,则由Execution Engine决定 加载的类信息存放于一块称为方法区的内存空间ÿ…...
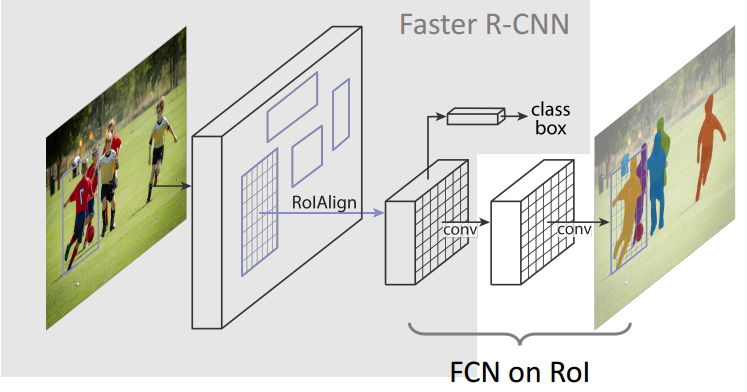
【实例分割】(一)Mask R-CNN详细介绍带python代码
目录 1.🍀🍀实例分割定义 2.🍀🍀Mask R-CNN 3.🍀🍀经典的实例分割算法 4.🍀🍀Mask R-CNN python代码 整理不易,欢迎一键三连!!!…...
面试官问我Redis怎么测,我一脸懵逼!
有些测试朋友来问我,redis要怎么测试?首先我们需要知道,redis是什么?它能做什么? redis是一个key-value类型的高速存储数据库。 redis常被用做:缓存、队列、发布订阅等。 所以,“redis要怎么测试…...

【Spring Boot】四种核心类的依赖关系:实体类、数据处理类、业务处理类、控制器类
//1.配置项目环境,创建Spring Boot项目。 //2.数据库设置,配置数据库。 //3.创建实体类,映射到数据库。 //4.创建数据处理层类,Repository //5.创建业务处理类,Service类 //6.创建控制器类,Controller类 Ar…...

opencv 进阶15-检测DoG特征并提取SIFT描述符cv2.SIFT_create()
前面我们已经了解了Harris函数来进行角点检测,因为角点的特性,这些角点在图像旋转的时候也可以被检测到。但是,如果我们放大或缩小图像时,就可能会丢失图像的某些部分,甚至有可能增加角点的质量。这种损失的现象需要一…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
