常见排序集锦-C语言实现数据结构
目录
排序的概念
常见排序集锦
1.直接插入排序
2.希尔排序
3.选择排序
4.堆排序
5.冒泡排序
6.快速排序
hoare
挖坑法
前后指针法
非递归
7.归并排序
非递归
排序实现接口
算法复杂度与稳定性分析

这里推荐一个网站 数据结构和算法动态可视化 (Chinese) - VisuAlgo
它可以让我们更加清晰的看清楚排序的过程。
排序实现接口
sort.h
#include<stdlib.h>
#include<stdio.h>
#include<assert.h>
#include<time.h>// 插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);// 选择排序
void SelectSort(int* a, int n);// 堆排序
void AdjustDwon(int* a, int n, int root);
void HeapSort(int* a, int n);// 冒泡排序
void BubbleSort(int* a, int n)// 快速排序递归实现// 1.快速排序hoare版本
int PartSort1(int* a, int left, int right);// 2.快速排序挖坑法
int PartSort2(int* a, int left, int right);// 3.快速排序前后指针法
int PartSort3(int* a, int left, int right);void QuickSort(int* a, int left, int right);// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)// 归并排序递归实现
void MergeSort(int* a, int n)// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
1.插入排序
思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。

void InsertSort(int* arr, int n)
{// i< n-1 最后一个位置就是 n-2for (int i = 0; i < n - 1; i++){//[0,end]的值有序,把end+1位置的值插入,保持有序int end = i;int tmp = arr[end + 1];while (end >= 0){if (tmp < arr[end]){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp; // why? end+1 //break 跳出 插入 因为上面end--;//为什么不在else那里插入?因为极端环境下,假设val = 0,那么end-- 是-1,不进入while , //所以要在外面插入}
}为什么这里 for 循环 i < n-1 ? 如图所示:

2.希尔排序
希尔排序又称缩小增量法,思想 :算法先将要排序的一组数按某个增量 gap 分成若干组,每组中记录的下标相差 gap .对每组中全部元素进行排序,然后再用一个较小的增量对它进行分组,在每组中再进行排序。当增量减到1时( == 直接插入排序),整个要排序的数被分成一组,排序完成。
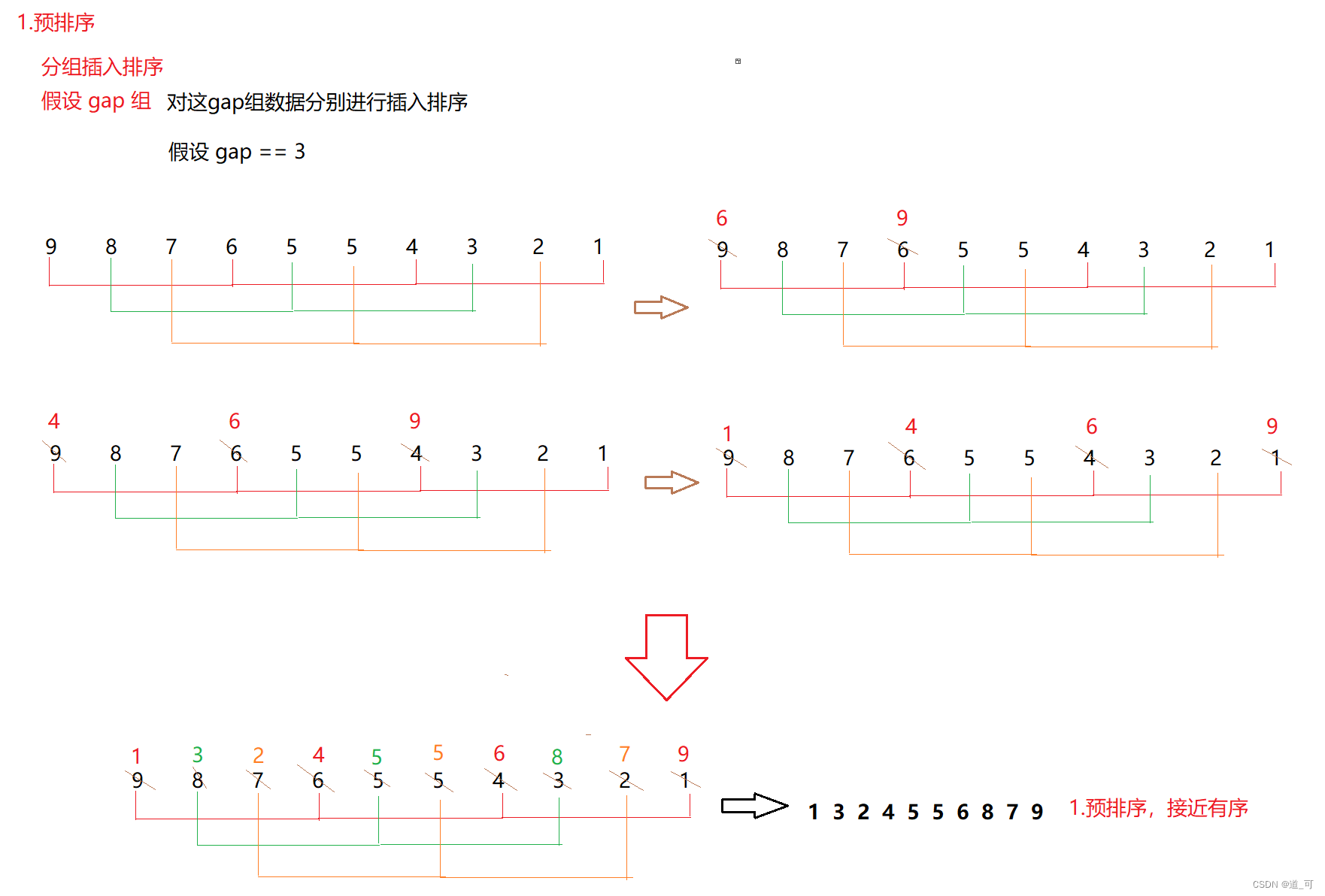
如下图:
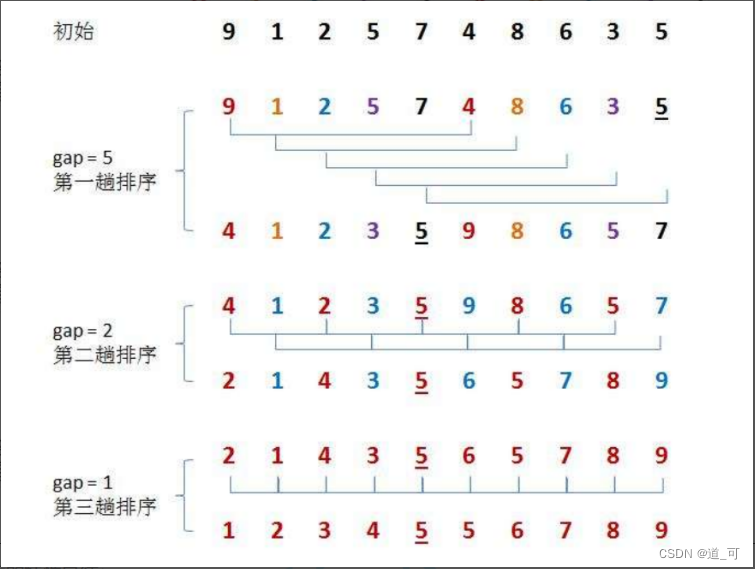
实现:①
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1; //gap = gap / 2;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i = i + gap){int end = i;int tmp = arr[end + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = tmp;}}
}②:在①的基础上进行简单的优化
void ShellSort(int* arr, int n)
{//gap > 1 时 ,预排序//gap = 1 时,直接插入排序int gap = n;while (gap > 1){gap = gap / 3 + 1; //加1意味着最后一次一定是1 ,当gap = 1 时,就是直接排序//gap = gap / 2;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (tmp < arr[end]){arr[end + gap] = arr[end];end = end - gap;}else{break;}}arr[end + gap] = tmp;}}}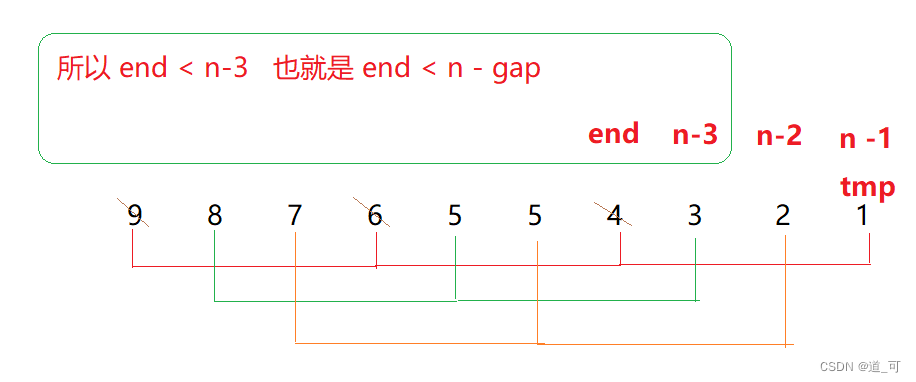
gap的取值?
这里看个人习惯,上述中是gap一开始为n,进入循环后每次 /3 ,之所以+1是为了保证最后一次循环gap一定为1。当然 /2 也是可以的,/2 就可以最后不用+1。
希尔排序的特性总结:
3.选择排序
思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
实现:这里简单做了一下优化,每次遍历不仅仅选出最小的,也选出最大的。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void SelectSort(int* arr, int n)
{assert(arr);int left = 0; //开始位置int right = n - 1; //结束位置while (left < right){int min = left;int max = left;for (int i = left + 1; i <= right; i++){if (arr[i] < arr[min])min = i;if (arr[i] > arr[max])max = i;}Swap(&arr[left], &arr[min]);//如果 left 和 max 重叠 ,那么要修正 max 的位置if (left == max){max = min;}Swap(&arr[right], &arr[max]);left++;right--;}}4.堆排序
思想:堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。

实现:建堆方式有两种,这里采用向下调整方式建堆
typedef int HPDataType;void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(HPDataType* arr, int size, int parent)//向下调整
{int child = parent * 2 + 1;while (child < size){if (arr[child + 1] > arr[child] && child + 1 < size){child++;}if (arr[child] > arr[parent]){Swap(&(arr[child]), &(arr[parent]));parent = child;child = (parent * 2) + 1;}else{break;}}}void HeapSort(int* arr, int n)
{//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}//排序int end = n - 1;while (end > 0){Swap(&(arr[0]), &(arr[end]));AdjustDown(arr, end, 0);end--;}}5.冒泡排序
思想:根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,冒泡排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
可参考:冒泡
实现:
void BubbleSort(int* arr, int n)
{assert(arr);for (int i = 0; i < n; i++){int flag = 1;for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);flag = 0;}}//如果没有发生交换,说明有序,直接跳出if (flag == 1)break;}}6.快速排序
思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
hoare版本


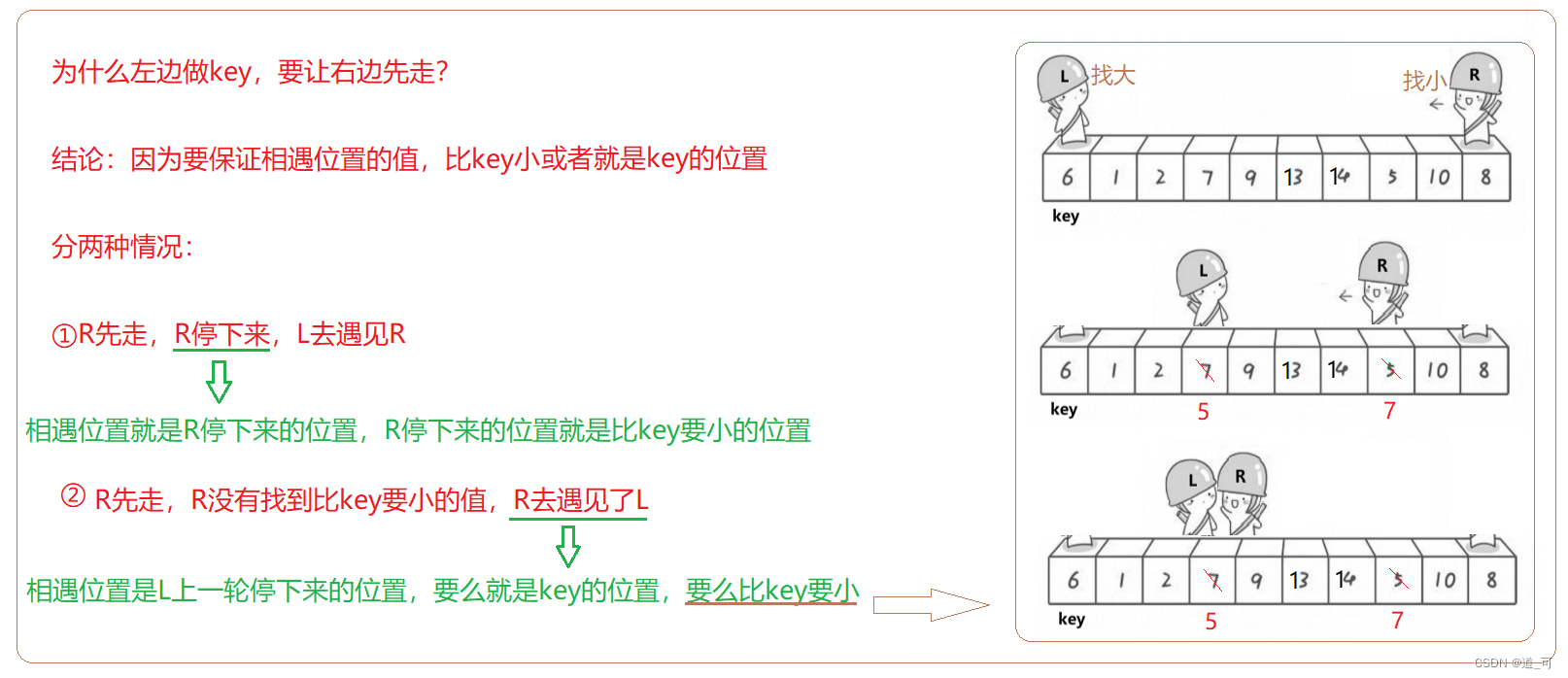
方法如下:
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int PartSort1(int* arr, int begin, int end)
{int left = begin;int right = end;//keyi 意味着保存的是 key 的位置int keyi = left;while (left < right){//右边先走,找小while (left < right && arr[right] >= arr[keyi]){right--;}//左边再走,找大while (left < right && arr[left] <= arr[keyi]){left++;}//走到这里意味着,右边的值比 key 小,左边的值比 key 大Swap(&arr[left], &arr[right]);}//走到这里 left 和 right 相遇 Swap(&arr[keyi], &arr[left]);keyi = left; //需要改变keyi的位置return keyi;
}挖坑法


方法如下:
int PartSort2(int* arr, int begin, int end)
{int key = arr[begin];int piti = begin;while (begin < end){//右边先走,找小,填到左边的坑里去,这个位置形成新的坑while (begin < end && arr[end] >= key){end--;}arr[piti] = arr[end];piti = end;//左边再走,找大while (begin < end && arr[begin] <= key){begin++;}arr[piti] = arr[begin];piti = begin;}//相遇一定是在坑位arr[piti] = key;return piti;}前后指针法

方法如下:
int PartSort3(int* arr, int begin, int end)
{int key = begin;int prev = begin;int cur = begin + 1;//优化-三数取中int midi = GetMidIndex(arr, begin, end);Swap(&arr[key], &arr[midi]);while (cur <= end){if (arr[cur] < arr[key] && prev != cur ){prev++;Swap(&arr[prev], &arr[cur]);}cur++;}Swap(&arr[key], &arr[prev]);key = prev;return key;
}实现:以上三种方法都是采用函数的方式实现,这样方便调用。另外,以上方法都是单趟排序,如果要实现完整的排序还是要采用递归的方法,类似于二叉树的前序遍历
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void QuickSort(int* arr, int begin,int end)
{//当区间不存在或者区间只要一个值,递归返回条件if (begin >= end){return;}if (end - begin > 20) //小区间优化一般在十几{//int keyi = PartSort1(arr, begin, end);//int keyi = PartSort2(arr, begin, end);int keyi = PartSort3(arr, begin, end);//[begin , keyi - 1] keyi [keyi + 1 , end]//如果 keyi 的左区间有序 ,右区间有序,那么整体就有序QuickSort(arr, begin, keyi - 1);QuickSort(arr, keyi + 1, end);}else{InsertSort(arr + begin, end - begin + 1);//为什么+begin,因为排序不仅仅排序左子树,还有右子树//为什么+1 ,因为这个区间是左闭右闭的区间.例:0-9 是10个数 所以+1}
}优化:
int GetMidIndex(int* arr, int begin, int end)
{//begin mid endint mid = (begin + end) / 2;if (arr[begin] < arr[mid]){if (arr[mid] < arr[end]){return mid;}else if(arr[begin] < arr[end]) //走到这里说明 mid 是最大的{return end;}else{return begin;}}else // arr[begin] > arr[mid]{if (arr[mid] > arr[end]){return mid;}else if (arr[begin] < arr[end]) // 走到这里就是 begin end 都大于 mid{return begin;}else{return end;}}
}非递归版本:
非递归版本需要用到栈,这里是用c语言实现,所以需要手动实现一个栈
如果使用c++的话,可以直接引用栈。
这里栈的实现暂时省略,后期会给出链接。这里暂时知道一下就行。
简图:

//非递归
//递归问题:极端场景下,深度太深,会出现栈溢出
//1.直接改成循环--例:斐波那契数列、归并排序
//2.用数据结构栈模拟递归过程
void QuickSortNonR(int* arr, int begin, int end)
{ST st;StackInit(&st);StackPush(&st, end);StackPush(&st, begin);while (!StackEmpty(&st)){int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);int keyi = PartSort3(arr, left, right);//[left , keyi - 1] keyi [keyi + 1 , right]if (keyi + 1 < right){StackPush(&st, right);StackPush(&st, keyi + 1);}if (left < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, left);}}StackDestory(&st);
}7.归并排序
思想:归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:

实现:
void _MergeSort(int* arr, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;//[begin mid] [mid+1,end]//递归_MergeSort(arr, begin, mid, tmp);_MergeSort(arr, mid + 1, end, tmp);//归并[begin mid] [mid+1,end]int left1 = begin;int right1 = mid;int left2 = mid + 1;int right2 = end;int i = begin;//这里之所以等于begin 而不是等于0 是因为可能是右子树而不是左子树 i为tmp数组下标while (left1 <= right1 && left2 <= right2){if (arr[left1] < arr[left2]){tmp[i++] = arr[left1++];}else{tmp[i++] = arr[left2++];}}//假如一个区间已经结束,另一个区间直接拿下来while (left1 <= right1){tmp[i++] = arr[left1++];}while (left2 <= right2){tmp[i++] = arr[left2++];}//把归并的数据拷贝回原数组 [begin mid] [mid+1,end]// +begin 是因为可能是右子树 例:[2,3][4,5]//+1 是因为是左闭右闭的区间 0-9 是10个数据memcpy(arr + begin, tmp + begin, (end - begin + 1) * sizeof(int));}void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc");exit(-1);}_MergeSort(arr, 0, n - 1, tmp);free(tmp);
}
非递归版本:
思想:这里不能使用栈或者队列,因为栈或者队列适合前序遍历的替换,但是归并排序的思想属于后序遍历,栈和队列的特性导致后期可能无法使用前面的空间。
这里因为是循环,所以可以设计一个变量 gap,当gap= 1 ,就一一进行归并,当gap = 2时,就两两进行归并,gap 每次 *2 。
如图:

代码如下:
void MergeSortNonR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//[i , i + gap-1] [i + gap , i + 2*gap-1]int left1 = i;int right1 = i + gap - 1;int left2 = i + gap;int right2 = i + 2 * gap - 1;int j = left1;while (left1 <= right1 && left2 <= right2){if (arr[left1] < arr[left2]){tmp[j++] = arr[left1++];}else{tmp[j++] = arr[left2++];}}while (left1 <= right1){tmp[j++] = arr[left1++];}while (left2 <= right2){tmp[j++] = arr[left2++];}}memcpy(arr, tmp, sizeof(int) * n);gap *= 2;}free(tmp);
}但是上述代码涉及到一个问题,因为假设要排序的数据不是2的次方倍就会产生问题(和数据的奇偶无关),就会越界。
例:

所以我们需要对代码进行优化, 优化可以从两个方面进行:
//1.归并完成全部拷贝回原数组
//采用修正边界的方法
//例:如果是9个数据 最后一个数据也要继续进行归并
//因为如果不归并的话,最后一次会全部拷贝回原数组,也就意味着9个数据,前8个归并,拷贝回去的最后一个数据因为没有进行归并而产生随机值。
//如果越界,就修正边界,继续进行归并
代码如下:
void MergeSortNonR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc");exit(-1);}int gap = 1;while (gap < n){//printf("gap=%d->", gap);for (int i = 0; i < n; i += 2 * gap){//[i , i + gap-1] [i + gap , i + 2*gap-1]int left1 = i;int right1 = i + gap - 1;int left2 = i + gap;int right2 = i + 2 * gap - 1;//监测是否出现越界//printf("[%d,%d][%d,%d]---", left1, right1, left2, right2);//修正边界if (right1 >= n){right1 = n - 1;//[left2 , right2] 修正为一个不存在的区间left2 = n;right2 = n - 1;}else if (left2 >= n){left2 = n;right2 = n - 1;}else if (right2 >= n){right2 = n - 1;}//printf("[%d,%d][%d,%d]---", left1, right1, left2, right2);int j = left1;while (left1 <= right1 && left2 <= right2){if (arr[left1] < arr[left2]){tmp[j++] = arr[left1++];}else{tmp[j++] = arr[left2++];}}while (left1 <= right1){tmp[j++] = arr[left1++];}while (left2 <= right2){tmp[j++] = arr[left2++];}}//printf("\n");memcpy(arr, tmp, sizeof(int) * n);gap *= 2;}free(tmp);
}2.归并一组数据就拷贝一组数据回原数组
这样,如果越界就直接break跳出循环,后面的数据不进行归并。
void MergeSortNonR_2(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//[i , i + gap-1] [i + gap , i + 2*gap-1]int left1 = i;int right1 = i + gap - 1;int left2 = i + gap;int right2 = i + 2 * gap - 1;//right1 越界 或者 left2 越界,则不进行归并if (right1 >= n || left2 > n){break;}else if (right2 >= n){right2 = n - 1;}int m = right2 - left1 + 1;//实际归并个数int j = left1;while (left1 <= right1 && left2 <= right2){if (arr[left1] < arr[left2]){tmp[j++] = arr[left1++];}else{tmp[j++] = arr[left2++];}}while (left1 <= right1){tmp[j++] = arr[left1++];}while (left2 <= right2){tmp[j++] = arr[left2++];}memcpy(arr+i, tmp+i, sizeof(int) * m);}gap *= 2;}free(tmp);
}以上两种方式的代码皆可,具体重要的还是思想。
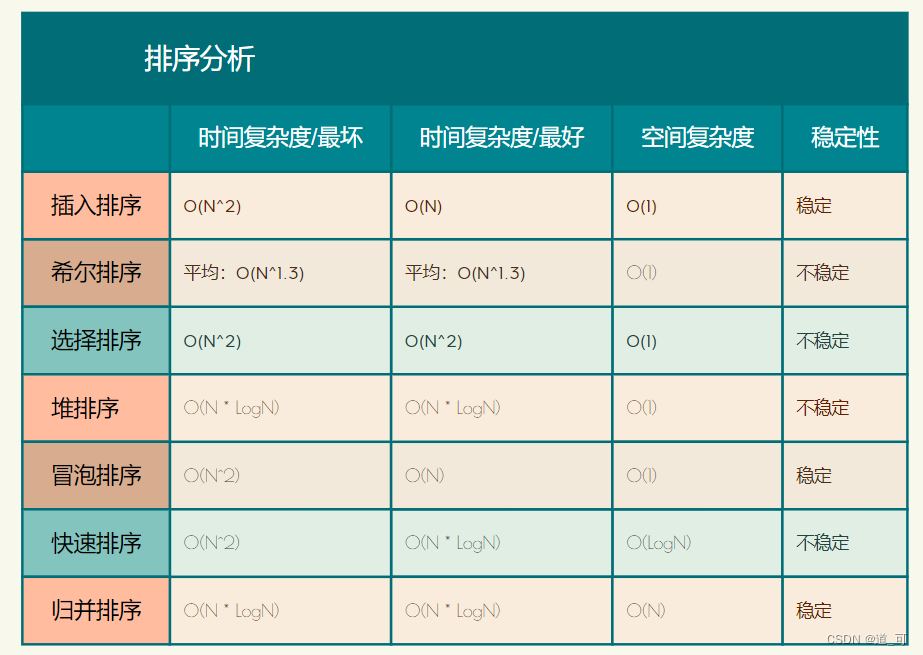
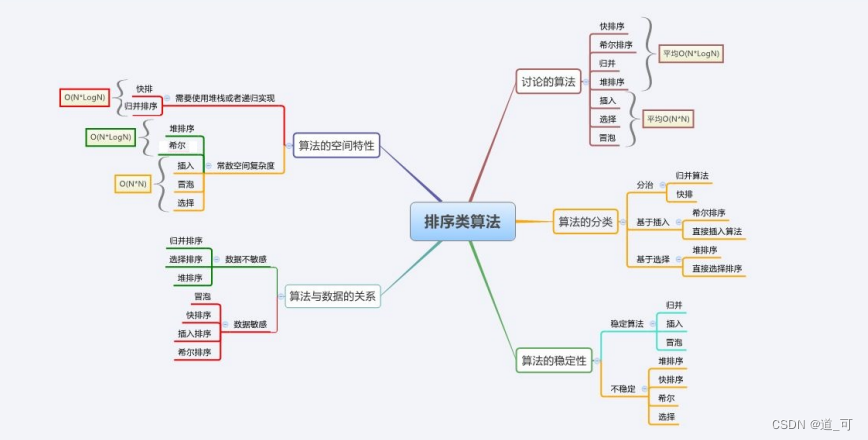
算法复杂度与稳定性分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
相关文章:

常见排序集锦-C语言实现数据结构
目录 排序的概念 常见排序集锦 1.直接插入排序 2.希尔排序 3.选择排序 4.堆排序 5.冒泡排序 6.快速排序 hoare 挖坑法 前后指针法 非递归 7.归并排序 非递归 排序实现接口 算法复杂度与稳定性分析 排序的概念 排序 :所谓排序,就是使一串记录&#…...

css 实现四角边框样式
效果如图 此图只实现 左下与右下边角样式 右上与左上同理 /* 容器 */ .card-mini {position: relative; } /* 左下*/ .card-mini::before {content: ;position: absolute;left: 0;bottom: 0;width: 20px;height: 20px;border-bottom: 2px solid #253d64;border-left: 2px so…...
机器学习深度学习——自注意力和位置编码(数学推导+代码实现)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——注意力分数(详细数学推导代码实现) 📚订阅专栏:机器学习…...

02.案列项目Demo
1.创建项目 1. 创建项目 用pycharm 选择对应的编译器,输入对应的文件名,点击创建项目。删除默认外层生成的template和DIRS 配置项: 2. 创建App 创建appo1的命令: python manage.py startapp app01 如果使用pycharm>tool>…...

PDF校对:追求文档的精准与完美
随着数字化时代的到来,PDF已经成为了多数机构和个人首选的文件格式,原因在于它的稳定性、跨平台特性以及统一的显示效果。但是,对于任何需要公开或正式发布的文档,确保其内容的准确性是至关重要的,这就是PDF校对显得尤…...
低代码解放生产力,助力企业高效发展
近年来,随着数字化转型的推进,企业对于软件开发的需求日益显著。然而,传统的软件开发模式通常需要耗费大量时间和资源,限制了企业的快速响应能力。为了解决这一难题,低代码开发平台应运而生,成为企业和开发…...

【前端从0开始】CSS——9、浮动
1. 浮动(float) 1.1 定义 float 属性定义元素向哪个方向浮动。之前这个属性应用于图像,使文本围绕在图像周围,不过在 CSS 中,任何元素都可以浮动。浮动元素会生成一个块级框,不论它本身是何种元素。 取值…...
如何在Moonriver网络上向社区代表委托投票权利
我们之前介绍了「社区代表」这一概念,想必大家对社区代表在治理中扮演的角色和地位有了一定的了解。 本文将介绍如何将您的投票权利委托给社区代表。请注意,在委托Token给社区代表这一过程中,并非将您的Token转移给任何人,而且此…...
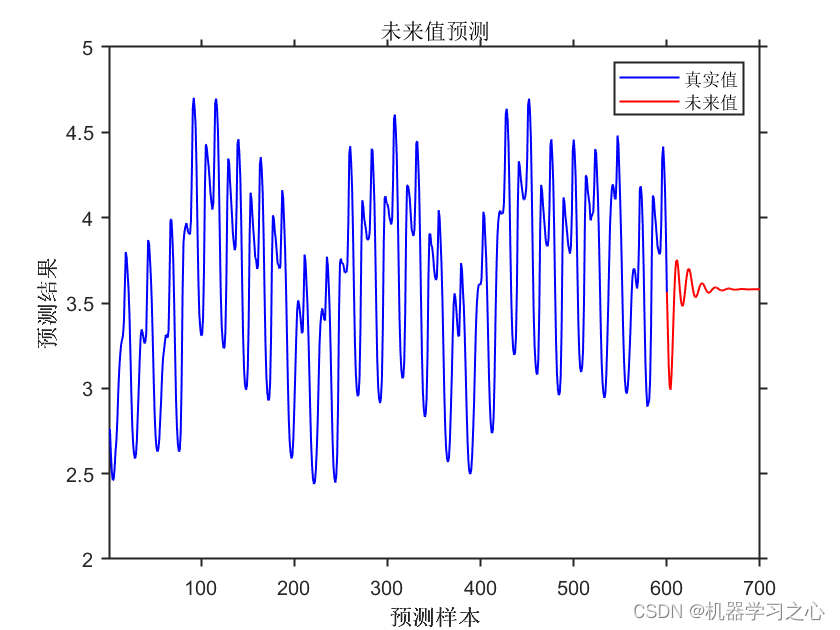
时序预测 | MATLAB实现基于CNN-GRU卷积门控循环单元的时间序列预测-递归预测未来(多指标评价)
时序预测 | MATLAB实现基于CNN-GRU卷积门控循环单元的时间序列预测-递归预测未来(多指标评价) 目录 时序预测 | MATLAB实现基于CNN-GRU卷积门控循环单元的时间序列预测-递归预测未来(多指标评价)预测结果基本介绍程序设计参考资料 预测结果 基本介绍 MATLAB实现基于CNN-GRU卷积…...

【李群李代数】李群控制器(lie-group-controllers)介绍——控制 SO(3) 空间中的系统的比例控制器Demo...
李群控制器SO(3)测试 测试代码是一个用于控制 SO(3) 空间中的系统的比例控制器。它通过计算控制策略来使当前状态逼近期望状态。该控制器使用比例增益 kp 进行参数化,然后进行一系列迭代以更新系统状态,最终检查状态误差是否小于给定的阈值。这个控制器用…...
PCI Express 总线)
DP读书:鲲鹏处理器 架构与编程(六)PCI Express 总线
处理器与服务器:PCI Express 总线 PCI Express 总线1. PCI Express 总线的特点a. 高速差分传输b. 串行传输c. 全双工端到端连接d. 基于多通道的数据传输方式e. 基于数据包的传输 2. PCI Express 总线的组成与拓扑结构a. 根复合体b. PCI Express桥c. 功能单元 3. PCI…...
Pyqt5-开源工具分解功能(文本拖拽)
开源第四篇:功能实现之拖拽功能与配置文件。 写这个功能的初衷,是因为,每次调试我都要手动敲命令,太麻烦了,想偷个懒,所以直接给这功能加上了,顺便衍生出了另一个想法,配置文件自动填写相关数据。 先看个简单的拖拽功能: 很明显吧,还是比较便捷的。所以我们本章,就在…...
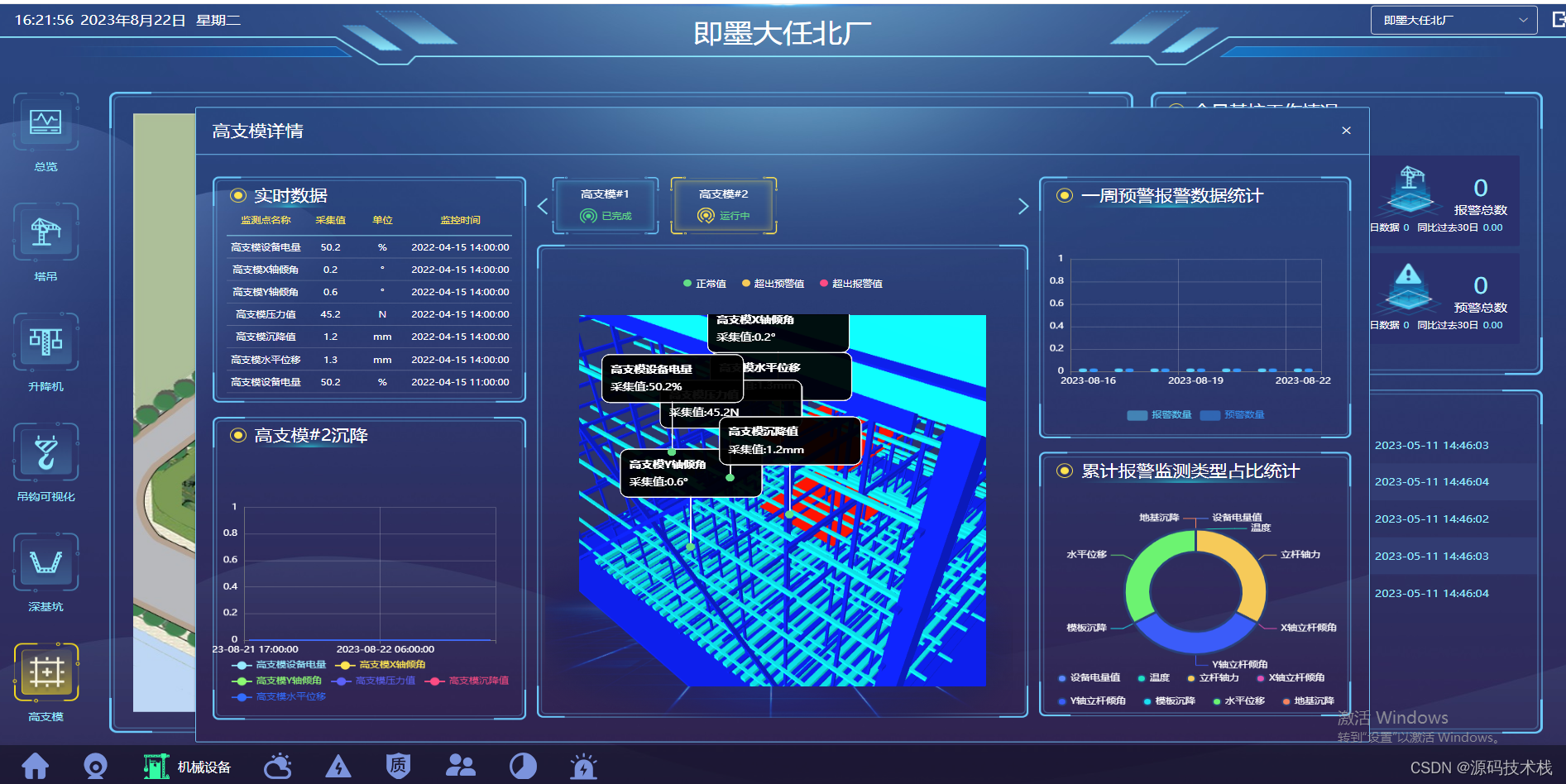
Java版B/S架构 智慧工地源码,PC、移动、数据可视化智慧大屏端源码
智慧工地是什么?智慧工地主要围绕绿色施工、安全管控、劳务管理、智能管理、集成总控等方面,帮助工地解决运营、管理方面各个难点痛点。在互联网的加持下促进项目现场管理的创新与发展,实现工程管理人员与工程施工现场的整合,构建…...

无涯教程-PHP - Session选项
从PHP7 起, session_start()()函数接受一系列选项,以覆盖在 php.ini 中设置的会话配置指令。这些选项支持 session.lazy_write ,默认情况下此函数为on,如果会话数据已更改,则会导致PHP覆盖任何会话文件。 添加的另一个…...

The Age of Data and AI: Challenges and Opportunities
Simply put Abstract: This paper examines the impact of the “Age of Data” on the field of artificial intelligence (AI). With the proliferation of digital technologies and advancements in data collection, storage, and processing, organizations now have ac…...
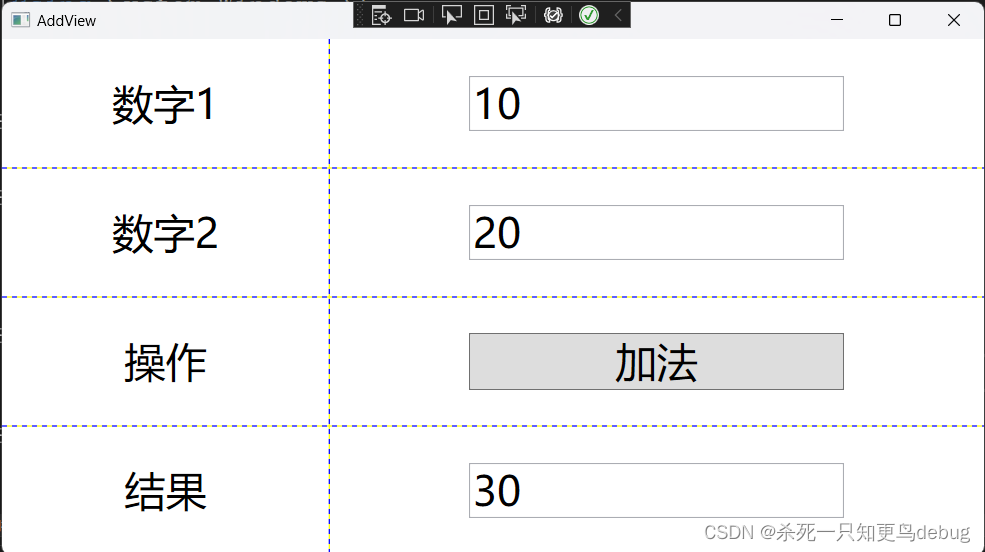
WPF 项目中 MVVM模式 的简单例子说明
一、概述 MVVM 是 Model view viewModel 的简写。MVVM模式有助于将应用程序的业务和表示逻辑与用户界面清晰分离。 几个概念的说明: model :数据,界面中需要的数据,最好不要加逻辑代码view : 视图就是用户看到的UI结构 xaml 文件viewModel …...
基于nginx禁用访问ip
一、背景 网络安全防护时,禁用部分访问ip,基于nginx可快速简单实现禁用。 二、操作 1、创建 conf.d文件夹 在nginx conf 目录下创建conf.d文件夹 Nginx 扩展配置文件一般在conf.d mkdir conf.d 2、新建blocksip.conf文件 在conf.d目录新建禁用ip的扩展配置文…...

【第三阶段】kotlin语言的内置函数let
1.使用普通方法对集合的第一个元素相加 fun main() {//使用普通方法对集合的第一个元素相加var list listOf(1,2,3,4,5)var value1list.first()var resultvalue1value1println(result) }执行结果 2.使用let内置函数对集合的第一个元素相加 package Stage3fun main() {//使用…...

【C++入门到精通】C++入门 —— 模版(template)
阅读导航 前言一、模版的概念二、函数模版1. 函数模板概念2. 函数模板定义格式3. 函数模板的原理4. 函数模版的实例化🚩隐式实例化🚩显式实例化 5. 函数模板的匹配原则 三、类模板1. 类模板的定义格式2. 类模板的实例化 四、非类型模板参数1. 概念2. 定义…...

ARM汇编【3】:LOAD/STORE MULTIPLE PUSH AND POP
LOAD/STORE MULTIPLE 有时一次加载(或存储)多个值更有效。为此,我们使用LDM(加载多个)和STM(存储多个)。这些指令有一些变化,基本上只在访问初始地址的方式上有所不同。这是…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
