当前位置： 首页 > news >正文

把matlab的m文件打包成单独的可执行文件

news 2025/12/17 8:42:01
  • 安装Matlab Compiler Adds-on
  • 在app里找到Application Compiler
    在这里插入图片描述
  • 选择要打包的文件
  • matlab单独的运行程序的话需要把依赖的库做成runtime. 这里有两个选项. 上面那个是需要对方在联网的情况下安装, 安装包较小.
  • 下面那个是直接把runtime打包成安装程序, 大概由你的程序依赖的库的多少决定.
    在这里插入图片描述

打包完第一个里就是runtime的安装包, 先安装这个.

第二个里面是你实际的程序, 如果安装完runtime就可以运行这个程序了.

相关文章：

把matlab的m文件打包成单独的可执行文件

安装Matlab Compiler Adds-on在app里找到Application Compiler 选择要打包的文件matlab单独的运行程序的话需要把依赖的库做成runtime. 这里有两个选项. 上面那个是需要对方在联网的情况下安装, 安装包较小.下面那个是直接把runtime打包成安装程序, 大概由你的程序依赖的库的多…...

编程日记 2023/8/24 1:49:55

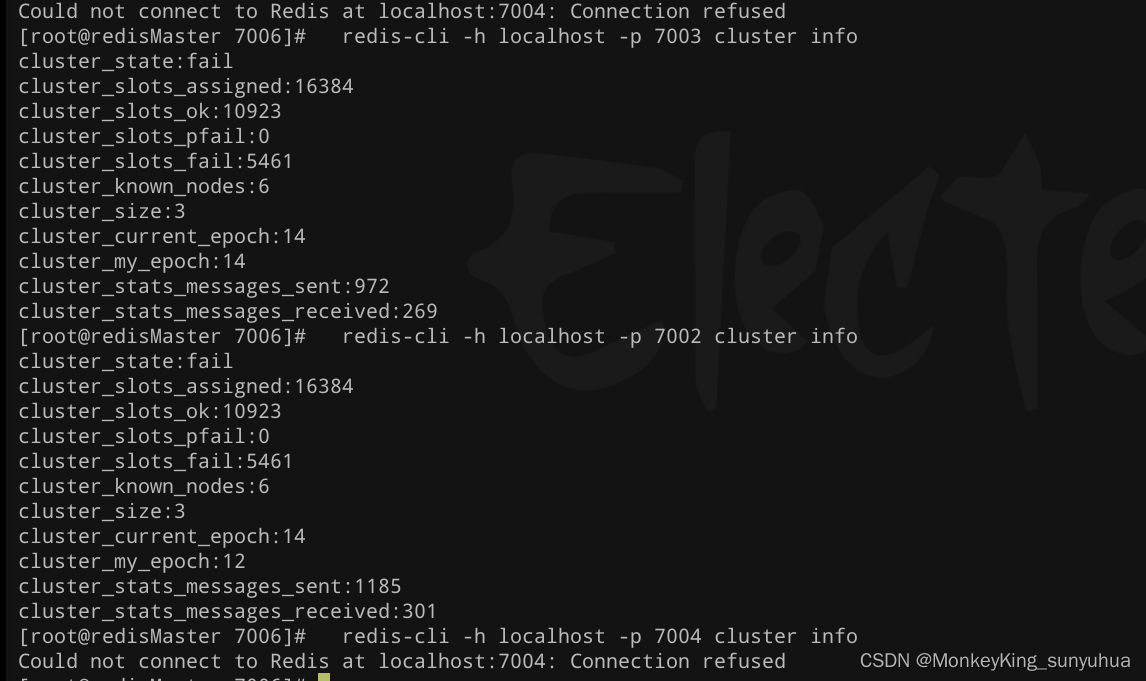
redis 6个节点（3主3从），始终一个节点不能启动

redis节点，始终有一个节点不能启动起来 1.修改了配置文件 protected-mode no，重启 修改了配置文件 protected-mode no，重启redis问题依然存在 2、查看/var/log/message的redis日志 Aug 21 07:40:33 redisMaster kernel: Out of memory: K…...

编程日记 2023/8/24 1:48:54

单体架构 Monolithic Architecture

单体架构（Monolithic Architecture） 单体架构是一种传统的软件架构模式，其中整个应用程序被构建为一个单一、完整的代码库和部署单元。 在单体架构中，所有的功能、模块和组件都打包在一起，通常使用同一种编程语言和技…...

编程日记 2023/8/24 1:47:53

HCIP的STP总结

目录 一、802.1D 一个交换网络内仅存在一棵生成树实例； 二、PVST cisco私有 基于vlan的生成树协议 三、PVST 在PVST的基础，兼容802.1q的trunk封装；且设计了部分的加速； 四、快速生成树 五、MSTP/MST/802.1S …...

编程日记 2023/8/24 1:46:50

Post Robot

一、题目 DT is a big fan of digital products. He writes posts about technological products almost everyday in his blog. But there is such few comments of his posts that he feels depressed all the day. As his best friend and an excellent programmer, DT as…...

编程日记 2023/8/24 1:45:49

HTML中，常用的布局方式

在HTML中&#xff0c;常用的布局方式有以下几种&#xff1a; 表格布局: 使用<table>、<tr>和<td>元素来创建一个表格布局。这种布局方式简单易懂&#xff0c;适用于需要展示数据的情况。但是不建议在网页布局中频繁使用表格布局&#xff0c;因为其结构较为复…...

编程日记 2023/8/24 1:44:48

uboot源码结构

一、uboot源码获取 uboot源码下载 http://www.denx.de/wiki/U-Boot/ uboot版本命名 前期:uboot-1.2.3 现在:uboot-2008.01 uboot版本选择 支持对应的硬件平台 相对成熟的版本&#xff08;资料多&#xff09; 二、uboot特点 代码结构清晰 支持丰富的处理器与开发板&#xf…...

编程日记 2023/8/24 1:43:44

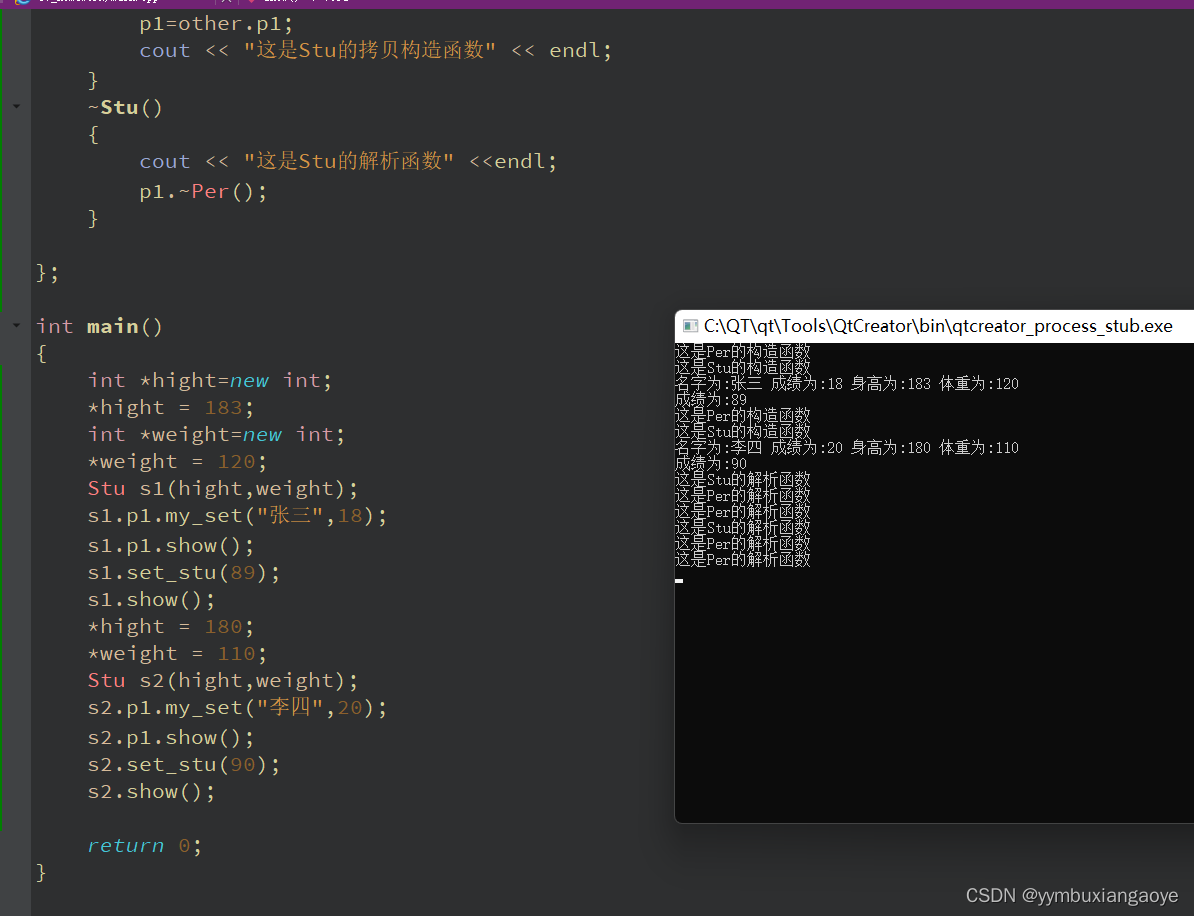
c++（8.23）类，this指针，构造函数，析构函数，拷贝构造函数

设计一个Per类&#xff0c;类中包含私有成员&#xff1a;姓名、年龄、指针成员身高、体重&#xff0c;再设计一个Stu类&#xff0c;类中包含私有成员&#xff1a;成绩、Per类对象 p1&#xff0c;设计这两个类的构造函数、析构函数和拷贝构造函数。 #include <iostream>u…...

编程日记 2023/8/24 1:42:41

前端网络相关知识(TCP和UDP的区别, TCP的三次握手)

tcp和udp的区别 TCP&#xff08;传输控制协议&#xff09;和UDP&#xff08;用户数据报协议&#xff09;是两种常用的互联网传输协议。它们在以下几个方面有所不同&#xff1a; 连接性&#xff1a;TCP是面向连接的协议&#xff0c;而UDP是无连接的协议。TCP在通信之前需要建立…...

编程日记 2023/8/24 1:41:39

大数据-玩转数据-Flink营销对账

一、说明 在电商网站中&#xff0c;订单的支付作为直接与营销收入挂钩的一环&#xff0c;在业务流程中非常重要。对于订单而言&#xff0c;为了正确控制业务流程&#xff0c;也为了增加用户的支付意愿&#xff0c;网站一般会设置一个支付失效时间&#xff0c;超过一段时间不支…...

编程日记 2023/8/24 1:40:38

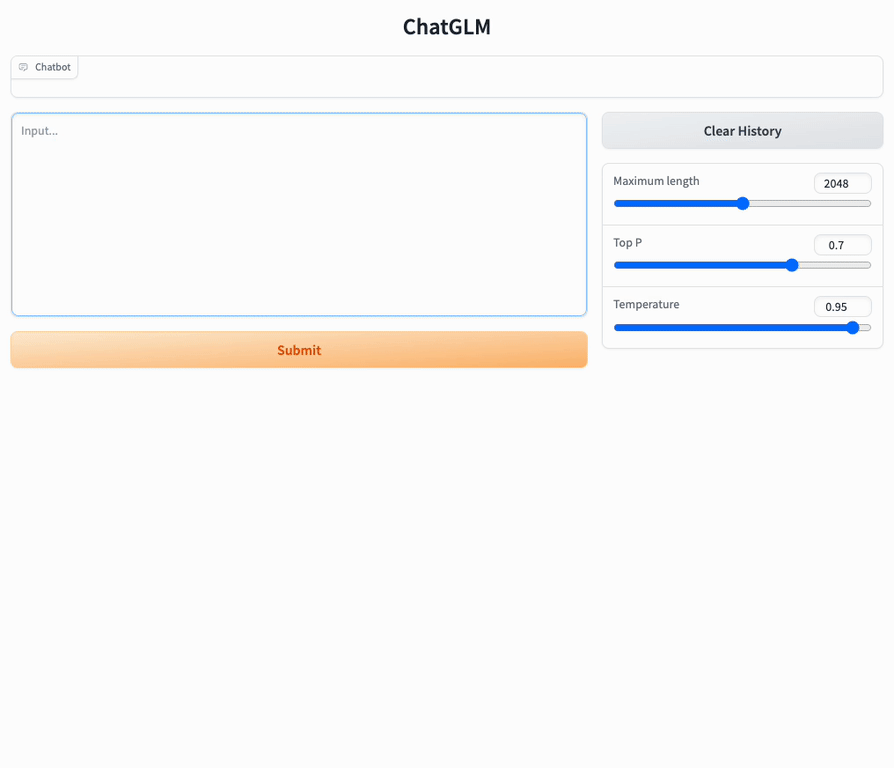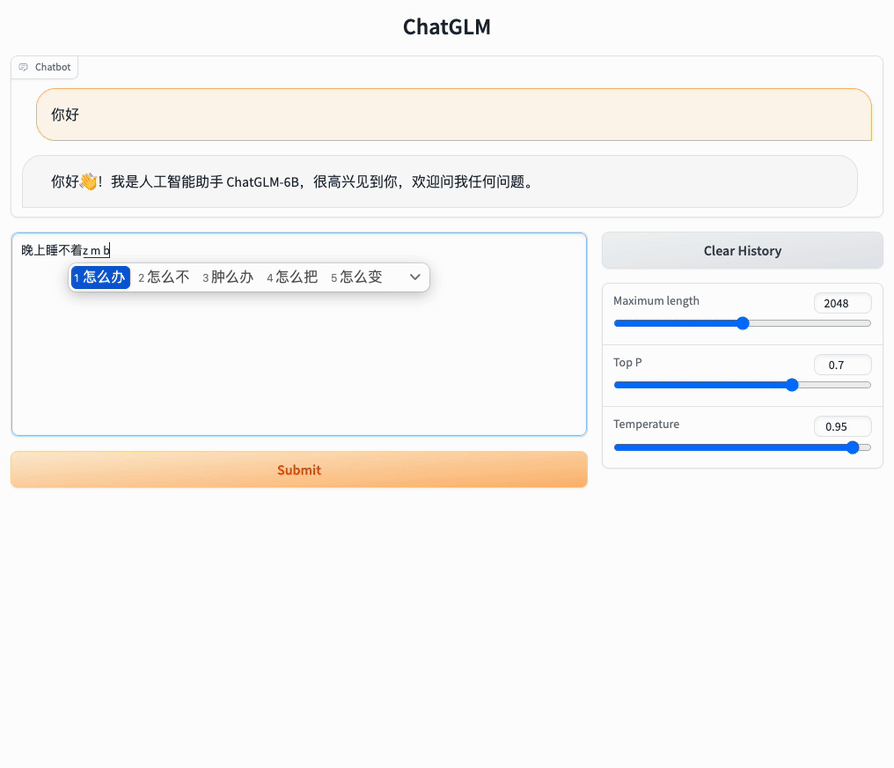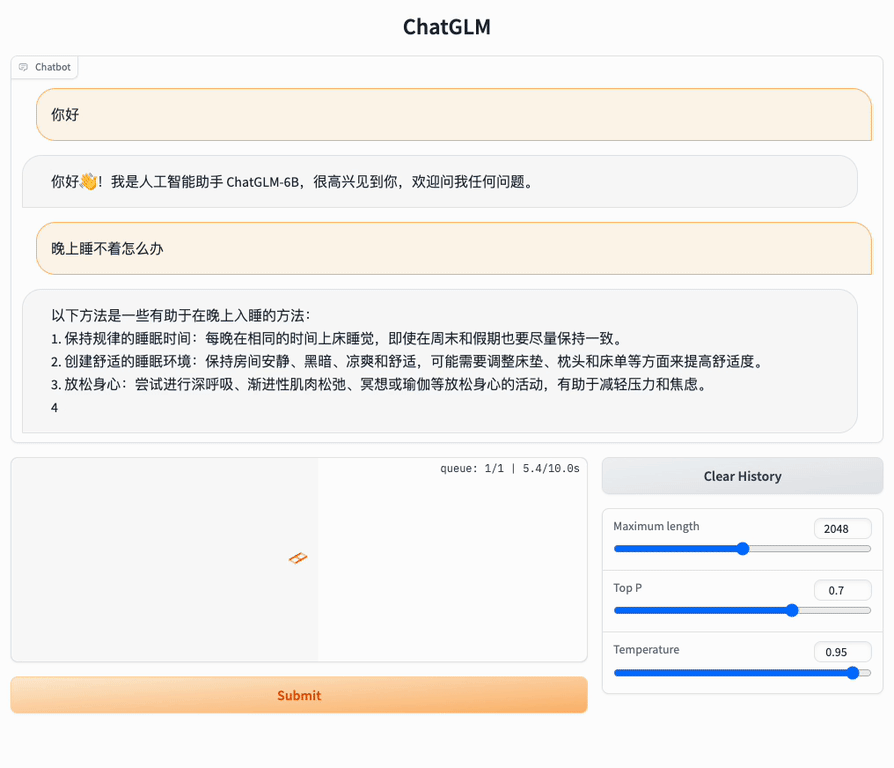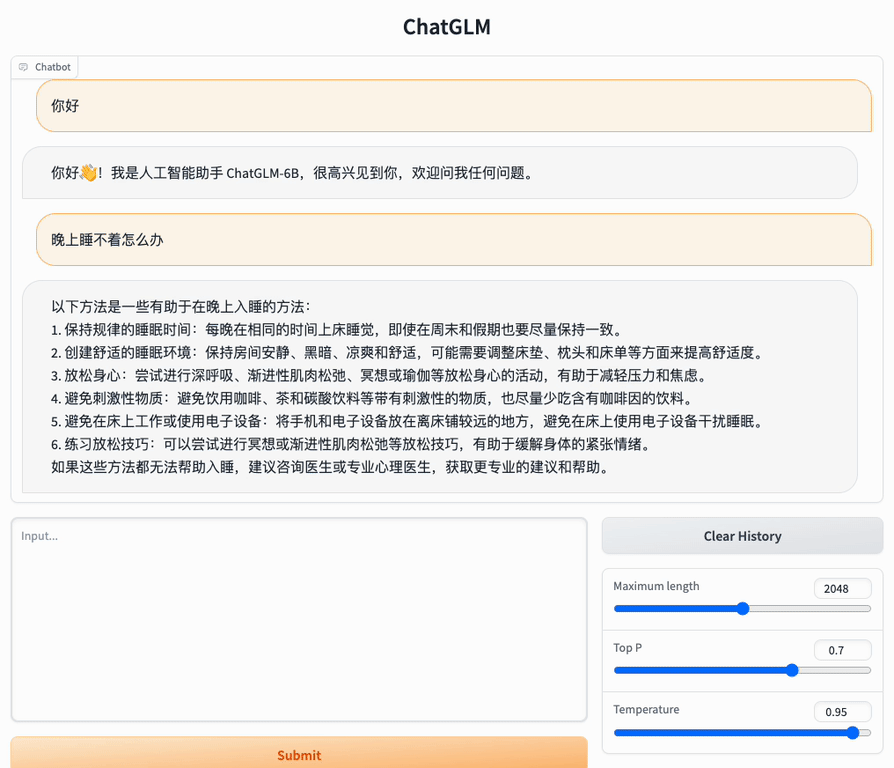
中英双语对话大语言模型：ChatGLM-6B

介绍 ChatGLM-6B 是一个开源的、支持中英双语的对话语言模型&#xff0c;基于 General Language Model (GLM) 架构&#xff0c;具有 62 亿参数。结合模型量化技术&#xff0c;用户可以在消费级的显卡上进行本地部署&#xff08;INT4 量化级别下最低只需 6GB 显存&#xff09;。…...

编程日记 2023/8/24 1:39:35

MES生产报工管理

一、MES生产报工管理的定义与功能&#xff1a; MES生产报工管理是指利用制造执行系统&#xff08;MES&#xff09;对生产过程进行实时监控、数据采集和分析&#xff0c;并及时记录和报告生产工单的实际完成情况。其主要功能包括&#xff1a; 1. 实时数据采集&#xff1a;通过…...

编程日记 2023/8/24 1:38:30

五、修改官方FreeRTOS例程(STM32F1)

1、官方源码下载 (1)进入FreeRTOS官网&#xff1a;FreeRTOS官网 (2)下载FreeRTOS。(选择带示例的下载) 2、删减目录 (1)下载后解压的FreeRTOS文件如下图所示。 (2)删除下图中红框勾选的文件。 FreeRTOS-Plus&#xff0c;FreeRTOS的生态文件&#xff0c;非必需的。tools&…...

编程日记 2023/8/24 1:37:29

pytorch基础实践-数据与预处理

文章目录 数据集Fashion-MNIST 数据集 数据预处理包的导入在Pytorch中进行 ETL利用torchvison包获取和处理数据集&#xff08;ET&#xff09; 访问数据集访问和查看 train_set 中的单个数据利用 DataLoader 成批访问数据 数据集 Fashion-MNIST 数据集 MNIST MNIST&#xff0c;…...

编程日记 2023/8/24 1:36:25

Java智慧工地系统源码（微服务+Java+Springcloud+Vue+MySQL）

智慧工地系统是依托物联网、互联网、AI、可视化建立的大数据管理平台&#xff0c;是一种全新的管理模式&#xff0c;能够实现劳务管理、安全施工、绿色施工的智能化和互联网化。围绕施工现场管理的人、机、料、法、环五大维度&#xff0c;以及施工过程管理的进度、质量、安全三…...

编程日记 2023/8/24 1:35:24

PV3D: A 3D GENERATIVE MODEL FOR PORTRAITVIDEO GENERATION 【2023 ICLR】

ICLR&#xff1a;International Conference on Learning Representations CCF-A 国际表征学习大会&#xff1a;深度学习的顶级会议 生成对抗网络(GANs)的最新进展已经证明了生成令人惊叹的逼真肖像图像的能力。虽然之前的一些工作已经将这种图像gan应用于无条件的2D人像视频生…...

编程日记 2023/8/24 1:34:21

Apache BeanUtils工具介绍

beanutils&#xff0c;顾名思义&#xff0c;是java bean的一个工具类&#xff0c;可以帮助我们方便的读取(get)和设置(set)bean属性值、动态定义和访问bean属性&#xff1b;细心的话&#xff0c;会发现其实JDK已经提供了一个java.beans包&#xff0c;同样可以实现以上功能&…...

编程日记 2023/8/24 1:33:20

java 原子操作 笔记

目录 java 变量原子操作 java byte[] 原子操作 java 变量原子操作 public class Counter {private int count 0;public synchronized void increment() {count;}public synchronized int getCount() {return count;} } java byte[] 原子操作 public class SharedArray {pr…...

编程日记 2023/8/24 1:32:18

什么是线程安全性问题？Java中有哪些常用的同步机制来解决线程安全性问题？

线程安全性问题是指在多线程环境下&#xff0c;多个线程同时访问和修改共享数据时可能引发的数据不一致、竞态条件和并发访问异常等问题。线程安全性问题的主要原因是多个线程之间的并发执行&#xff0c;导致数据的访问和修改顺序不确定&#xff0c;从而产生不一致的结果。 为…...

编程日记 2023/8/24 1:31:17

Gitlab 安装全流程

Version&#xff1a;gitlab-ce:16.2.4-ce.0 简介 Gitlab 是一个开源的 Git 代码仓库系统&#xff0c;可以实现自托管的 Github 项目&#xff0c;即用于构建私有的代码托管平台和项目管理系统。系统基于 Ruby on Rails 开发&#xff0c;速度快、安全稳定。它拥有与 Github 类似…...

编程日记 2023/8/24 1:30:14

19c补丁后oracle属主变化，导致不能识别磁盘组

补丁后服务器重启&#xff0c;数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后&#xff0c;存在与用户组权限相关的问题。具体表现为&#xff0c;Oracle 实例的运行用户&#xff08;oracle&#xff09;和集…...

编程新知 2025/12/15 19:26:43

23-Oracle 23 ai 区块链表（Blockchain Table）

小伙伴有没有在金融强合规的领域中遇见&#xff0c;必须要保持数据不可变&#xff0c;管理员都无法修改和留痕的要求。比如医疗的电子病历中&#xff0c;影像检查检验结果不可篡改行的&#xff0c;药品追溯过程中数据只可插入无法删除的特性需求&#xff1b;登录日志、修改日志…...

编程新知 2025/12/15 13:10:05

Debian系统简介

目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版&#xff…...

编程新知 2025/12/16 8:10:14

Objective-C常用命名规范总结

【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名&#xff08;Class Name)2.协议名&#xff08;Protocol Name)3.方法名&#xff08;Method Name)4.属性名&#xff08;Property Name&#xff09;5.局部变量/实例变量&#xff08;Local / Instance Variables&…...

编程新知 2025/12/14 22:33:06

家政维修平台实战20：权限设计

目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系&#xff0c;主要是分成几个表&#xff0c;用户表我们是记录用户的基础信息&#xff0c;包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题&#xff0c;不同的角色&#xf…...

编程新知 2025/12/14 1:11:38

C++中string流知识详解和示例

一、概览与类体系 C 提供三种基于内存字符串的流&#xff0c;定义在 <sstream> 中&#xff1a; std::istringstream&#xff1a;输入流&#xff0c;从已有字符串中读取并解析。std::ostringstream&#xff1a;输出流&#xff0c;向内部缓冲区写入内容&#xff0c;最终取…...

编程新知 2025/11/30 11:30:47

日常一水C

多态 言简意赅&#xff1a;就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过&#xff0c;当子类和父类的函数名相同时&#xff0c;会隐藏父类的同名函数转而调用子类的同名函数&#xff0c;如果要调用父类的同名函数&#xff0c;那么就需要对父类进行引用&#…...

编程新知 2025/9/30 22:37:58

命令行关闭Windows防火墙

命令行关闭Windows防火墙 引言一、防火墙：被低估的"智能安检员"二、优先尝试！90%问题无需关闭防火墙方案1：程序白名单（解决软件误拦截）方案2：开放特定端口（解决网游/开发端口不通）三、命令行极速关闭方案方法一：PowerShell（推荐Win10/11）​方法二：CMD命令…...

编程新知 2025/8/27 20:07:03

java+webstock

maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...

编程新知 2025/10/20 16:10:30

性能优化中，多面体模型基本原理

1&#xff09;多面体编译技术是一种基于多面体模型的程序分析和优化技术&#xff0c;它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象&#xff0c;通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中&#xff0…...

编程新知 2025/12/13 17:46:46