【考研数学】线形代数第三章——向量 | 2)向量组相关性与线性表示的性质,向量组的等价、极大线性无关组与秩
文章目录
- 引言
- 二、向量组的相关性与线性表示
- 2.3 向量组相关性与线性表示的性质
- 三、向量组等价、向量组的极大线性无关组与秩
- 3.1 基本概念
- 写在最后
引言
承接前文,我们来学习学习向量组相关性与线性表示的相关性质
二、向量组的相关性与线性表示
2.3 向量组相关性与线性表示的性质
性质 1 —— 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关的充分必要条件是向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 中至少有一个向量可由其余向量线性表示。
证明: 必要性:设向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关,则存在一组不全为零的常数 k 1 , k 2 , … , k n k_1,k_2,\dots,k_n k1,k2,…,kn ,使得 k 1 α 1 + k 2 α 2 + ⋯ + k n α n = 0 , k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n=0, k1α1+k2α2+⋯+knαn=0, 不妨设某一不为零的常数为 k 1 k_1 k1 ,即 k 1 ≠ 0 k_1 \ne 0 k1=0 ,则 α 1 = − k 2 k 1 α 2 − ⋯ − k n k 1 α n , \alpha_1=\frac{-k_2}{k_1}\alpha_2-\dots-\frac{k_n}{k_1}\alpha_n, α1=k1−k2α2−⋯−k1knαn, 即向量 α 1 \alpha_1 α1 可由其余向量线性表示。
充分性:设存在常数 l 1 , l 2 , … , l k − 1 , l k + 1 , … , l n l_1,l_2,\dots,l_{k-1},l_{k+1},\dots,l_n l1,l2,…,lk−1,lk+1,…,ln(缺少 l k l_k lk) ,使得 α k = l 1 α 1 + ⋯ + l k − 1 α k − 1 + ⋯ + l n α n \alpha_k=l_1\alpha_1+\dots+l_{k-1}\alpha_{k-1}+\dots+l_n\alpha_n αk=l1α1+⋯+lk−1αk−1+⋯+lnαn 则有: l 1 α 1 + l 2 α 2 + ⋯ + l k − 1 α k − 1 + ( − 1 ) α k + ⋯ + l n α n = 0 l_1\alpha_1+l_2\alpha_2+\dots+l_{k-1}\alpha_{k-1}+\pmb{(-1)\alpha_k}+\dots+l_n\alpha_n=0 l1α1+l2α2+⋯+lk−1αk−1+(−1)αk+⋯+lnαn=0 ,因为存在系数不为 0 ,所以向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关。
1,一个向量线性相关的充要条件是该向量为零向量。
2,两个向量线性相关的充要条件是两个向量成比例。
3,含有零向量的向量组一定线性相关。
性质 2 —— 设向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关,则:
(1)若 α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,b 线性相关,则向量 b b b 可由 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 唯一线性表示。
(2) α 1 , α 2 , … , α n , b \pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} α1,α2,…,αn,b 线性无关的充要条件是向量 b b b 不可由 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示。
性质 3 —— 若一个向量组线性无关,则该向量组的任何部分向量组都线性无关。
性质 4 —— 若向量组有一个部分向量组线性相关,则该向量组一定线性相关。
性质 5 —— 设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为 n n n 个 n n n 维向量,则 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关的充要条件是 ∣ α 1 , α 2 , … , α n ∣ ≠ 0 |\pmb{\alpha_1,\alpha_2,\dots,\alpha_n}| \ne 0 ∣α1,α2,…,αn∣=0 ,即这些向量构成的行列式不为 0 。
证明: α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关,即对应齐次方程组只有零解,故系数行列式不为 0 。
性质 6 —— 设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为 n n n 个 m m m 维向量,若 m < n m < n m<n ,则向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 必线性相关。
(1)向量组中向量的个数对应齐次线性方程组未知数的个数。向量组中向量的个数越多,齐次线性方程组中未知数的个数越多,其产生自由变量的可能性也越大,从而齐次线性方程组有非零解的可能性增加,即向量线性相关的可能性增加,故增加向量的个数后线性相关的可能性增加。
(2)向量组中向量的维数对应齐次线性方程组方程的个数,维数越多,齐次线性方程组方程的个数越多,只有零解的可能性增加,即向量线性无关的可能性增加,故增加向量的维数后线性无关的可能性增加。
性质 7 —— 设向量组 α 1 ′ , α 2 ′ , … , α n ′ \pmb{\alpha_1',\alpha_2',\dots,\alpha_n'} α1′,α2′,…,αn′ 为向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 的扩充向量组(即添加了维数),若向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关,则向量组 α 1 ′ , α 2 ′ , … , α n ′ \pmb{\alpha_1',\alpha_2',\dots,\alpha_n'} α1′,α2′,…,αn′ 线性无关,反之不对。
反例:如原向量组 α 1 = ( 1 , 0 ) T , α 2 = ( 0 , 1 ) T , α 3 = ( 0 , 0 ) T \pmb{\alpha_1=(1,0)^T,\alpha_2=(0,1)^T,\alpha_3=(0,0)^T} α1=(1,0)T,α2=(0,1)T,α3=(0,0)T ,扩充后 α 1 ′ = ( 1 , 0 , 0 ) T , α 2 ′ = ( 0 , 1 , 0 ) T , α 3 ′ = ( 0 , 0 , 1 ) T \pmb{\alpha_1'=(1,0,0)^T,\alpha_2'=(0,1,0)^T,\alpha_3'=(0,0,1)^T} α1′=(1,0,0)T,α2′=(0,1,0)T,α3′=(0,0,1)T ,其构成的行列式为 1 ≠ 0 1 \ne 0 1=0 ,故向量组 α 1 ′ , α 2 ′ , α 3 ′ \pmb{\alpha_1',\alpha_2',\alpha_3'} α1′,α2′,α3′ 线性无关,但原向量组含有零向量,线性相关。
性质 8 —— 设向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为两两正交的非零向量组,则 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关,反之不对。
证明: 令 k 1 α 1 + k 2 α 2 + ⋯ + k n α n = 0 k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n=0 k1α1+k2α2+⋯+knαn=0 ,由 ( α 1 , k 1 α 1 + k 2 α 2 + ⋯ + k n α n ) = ( α 1 , 0 ) = k 1 ( α 1 , α 1 ) + k 2 ( α 1 , α 2 ) + ⋯ + k n ( α 1 , α n ) = 0 (\alpha_1,k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n)=(\alpha_1,0)=k_1(\alpha_1,\alpha_1)+k_2(\alpha_1,\alpha_2)+\dots+k_n(\alpha_1,\alpha_n)=0 (α1,k1α1+k2α2+⋯+knαn)=(α1,0)=k1(α1,α1)+k2(α1,α2)+⋯+kn(α1,αn)=0 且向量组两两正交可得 k 1 ( α 1 , α 1 ) = 0 k_1(\alpha_1,\alpha_1)=0 k1(α1,α1)=0 ,又 α 1 \alpha_1 α1 为零,故 k 1 = 0 k_1 = 0 k1=0 。
则 k 2 α 2 + ⋯ + k n α n = 0 k_2\alpha_2+\dots+k_n\alpha_n=0 k2α2+⋯+knαn=0 ,由 ( α 2 , k 2 α 2 + ⋯ + k n α n ) = ( α 2 , 0 ) = k 2 ( α 2 , α 2 ) + ⋯ + k n ( α 2 , α n ) = 0 (\alpha_2,k_2\alpha_2+\dots+k_n\alpha_n)=(\alpha_2,0)=k_2(\alpha_2,\alpha_2)+\dots+k_n(\alpha_2,\alpha_n)=0 (α2,k2α2+⋯+knαn)=(α2,0)=k2(α2,α2)+⋯+kn(α2,αn)=0 且向量组两两正交可得 k 2 ( α 2 , α 2 ) = 0 k_2(\alpha_2,\alpha_2)=0 k2(α2,α2)=0 ,又 α 2 \alpha_2 α2 为零,故 k 2 = 0 k_2 = 0 k2=0 。同理可得到 k n = 0 k_n=0 kn=0 ,故向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关。
三、向量组等价、向量组的极大线性无关组与秩
3.1 基本概念
向量组等价 —— 若两个向量组维数相同,且可以相互线性表示,称两个向量组等价。
等价的两个向量组,向量个数不一定相同。
向量组的极大线性无关组与秩 —— 设 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 为一组向量,若满足:
(1)向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 存在 r r r 个向量线性无关;
(2)任意 r + 1 r+1 r+1 个向量(不一定有)一定线性相关,
称 r r r 个线性无关的向量构成的向量组为向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 的极大线性无关组,极大线性无关组所含向量的个数称为向量的秩。
怎么样?是不是和矩阵的秩很像,传送门。
可由其余向量线性表示的向量为向量组的多余向量,求向量组的极大线性无关组,从本质上说其实是去掉多余向量的过程。
向量组的极大线性无关组不一定具有唯一性。
向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 的极大线性无关组为本身的充要条件为该向量组的秩为 n . n. n.
令向量组 A : α 1 , α 2 , … , α n ; B : α 1 , α 2 , … , α n , b A:\pmb{\alpha_1,\alpha_2,\dots,\alpha_n};B:\pmb{\alpha_1,\alpha_2,\dots,\alpha_n,b} A:α1,α2,…,αn;B:α1,α2,…,αn,b ,则向量组 A , B A,B A,B 的秩有两种情形:
(1) A A A 的秩和 B B B 的秩相等,其充要条件是 b b b 可由 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示。
(2) A A A 的秩比 B B B 的秩少 1 ,其充要条件是 b b b 不可由 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性表示。
令 A = [ α 1 , α 2 , … , α n ] A=[\pmb{\alpha_1,\alpha_2,\dots,\alpha_n}] A=[α1,α2,…,αn] ,若矩阵 A A A 经过有限次初等列变换化为 B = [ β 1 , β 2 , … , β n ] B=[\pmb{\beta_1,\beta_2,\dots,\beta_n}] B=[β1,β2,…,βn] ,则向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 和 向量组 β 1 , β 2 , … , β n \pmb{\beta_1,\beta_2,\dots,\beta_n} β1,β2,…,βn 等价。
矩阵等价也是这个定义,可以初等变换得到。
写在最后
关于向量秩的性质以及剩余内容,放到后面吧。
到现在为止其实我们已经接触了矩阵、向量、线性方程组了,关于向量的秩和方程组解的关系使我开始联想到矩阵和方程组的关系,而矩阵又是由方程组构成的,让人有些着迷。我打算下一篇就先把这三个给整理一下,不等到学线性方程组的时候了。O.o
相关文章:
向量组相关性与线性表示的性质,向量组的等价、极大线性无关组与秩)
【考研数学】线形代数第三章——向量 | 2)向量组相关性与线性表示的性质,向量组的等价、极大线性无关组与秩
文章目录 引言二、向量组的相关性与线性表示2.3 向量组相关性与线性表示的性质 三、向量组等价、向量组的极大线性无关组与秩3.1 基本概念 写在最后 引言 承接前文,我们来学习学习向量组相关性与线性表示的相关性质 二、向量组的相关性与线性表示 2.3 向量组相关性…...

Java中调用Linux脚本
在Java中,可以使用ProcessBuilder类来调用Linux脚本。以下是一个简单的示例,展示了如何在Java中调用Linux脚本: 创建一个Linux脚本文件(例如:myscript.sh),并在其中编写需要执行的命令。确保脚…...
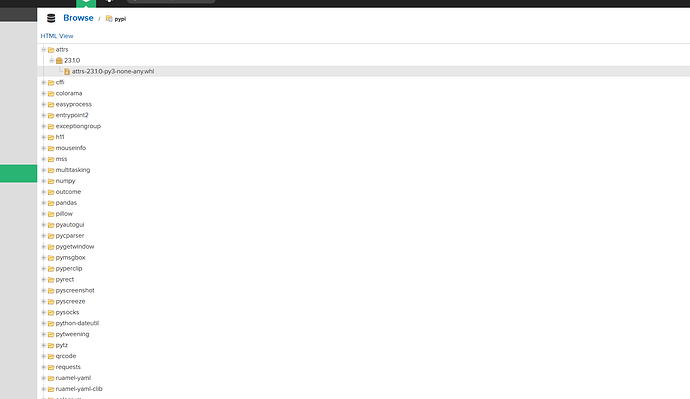
Nexus 如何配置 Python 的私有仓库
Nexus 可作为一个代理来使用。 针对一些网络环境不好的公司,可以通过配置 Nexus 来作为远程的代理。 Group 概念 Nexus 有一个 Group 的概念,我们可以认为一个 Nexus 仓库的 Group 就是很多不同的仓库的集合。 从下面的配置中我们可以看到࿰…...
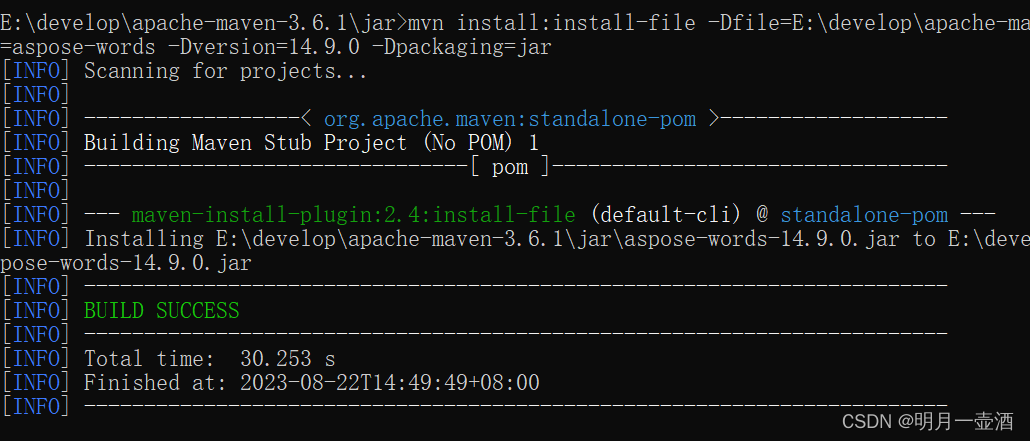
Maven 配置文件修改及导入第三方jar包
设置java和maven的环境变量 修改maven配置文件 (D:\app\apache-maven-3.5.0\conf\settings.xml,1中环境变量对应的maven包下的conf) 修改131行左右的mirror,设置阿里云的仓库地址 <mirror> <id>alimaven</id&g…...
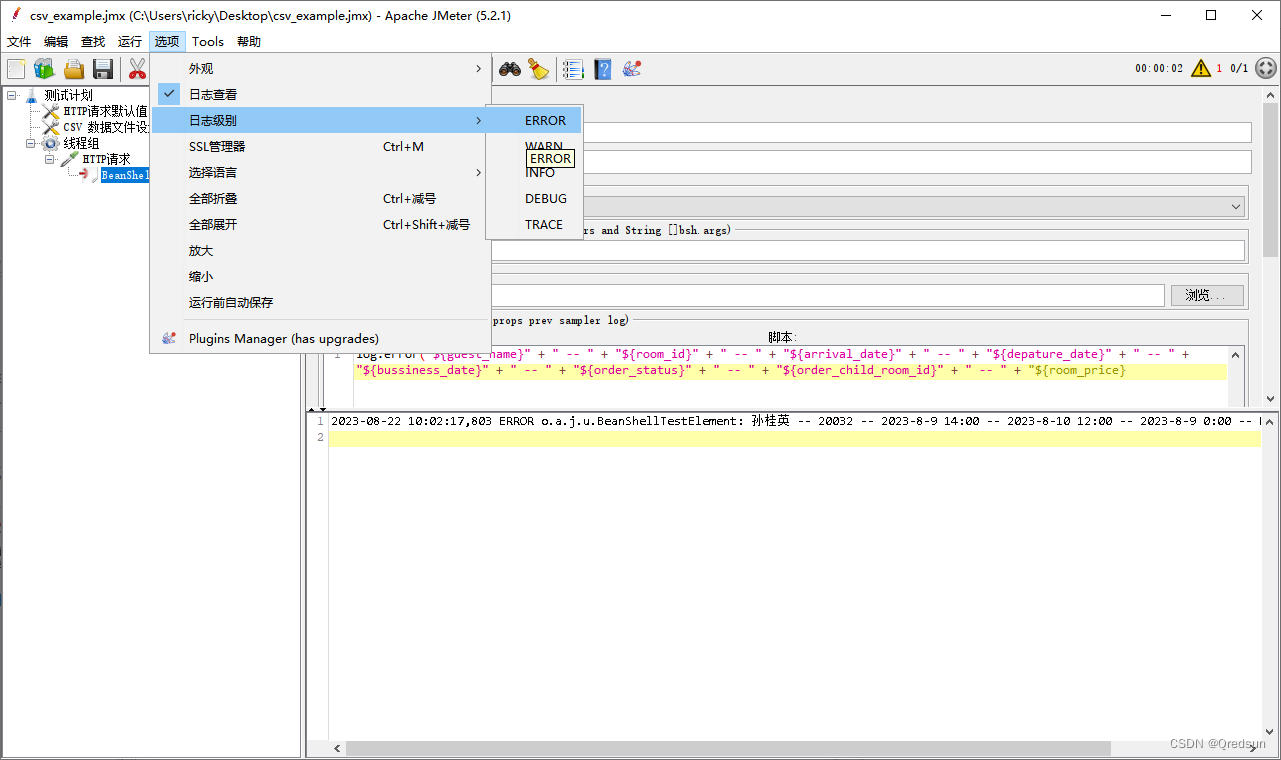
jmeter CSV 数据文件设置
创建一个CSV数据文件:使用任何文本编辑器创建一个CSV文件,将测试数据按照逗号分隔的格式写入文件中。例如: room_id,arrival_date,depature_date,bussiness_date,order_status,order_child_room_id,guest_name,room_price 20032,2023-8-9 14:…...

【SA8295P 源码分析】20 - GVM Android Kernel NFS Support 配置
【SA8295P 源码分析】20 - GVM Android Kernel NFS Support 配置 系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码分析】20 - GVM Android Kernel NFS Support 配置》 # make menuconfigFile systems ---> [*] Network File Sy…...

c++都补了c语言哪些坑?
目录 1.命名空间 1.1 定义 1.2 使用 2.缺省参数 2.1 概念 2.2 分类 3.函数重载 4.引用 4.1 概念 4.2 特性 4.3 常引用 4.4 引用和指针的区别 5.内联函数 1.命名空间 在 C/C 中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称将…...

【C语言】C语言用数组算平均数,并输出大于平均数的数
题目 让用户输入一系列的正整数,最后输入“-1”表示输入结束,然后程序计算出这些数的平均数,最后输出输入数字的个数和平均数以及大于平均数的数 代码 #include<stdio.h> int main() {int x;double sum 0;int cnt 0;int number[100…...

「UG/NX」Block UI 体收集器BodyCollector
✨博客主页何曾参静谧的博客📌文章专栏「UG/NX」BlockUI集合📚全部专栏「UG/NX」NX二次开发「UG/NX」BlockUI集合「VS」Visual Studio「QT」QT5程序设计「C/C+&#...

金九银十面试题之《JVM》
🐮🐮🐮 辛苦牛,掌握主流技术栈,包括前端后端,已经7年时间,曾在税务机关从事开发工作,目前在国企任职。希望通过自己的不断分享,可以帮助各位想或者已经走在这条路上的朋友…...

wireshark | 过滤筛选总结
wireshark 是一款开源抓包工具。比如与服务器的请求响应、tcp三次握手/四次挥手 场景:在linux环境下使用tcpdump -w 然后把爬的数据写入指定的XXX.pcap 然后在wireshark中导入该文件XXX.pcap 使用下面的过滤方式进行过滤 分析数据就可以了 #直接看 不需要硬背 和s…...
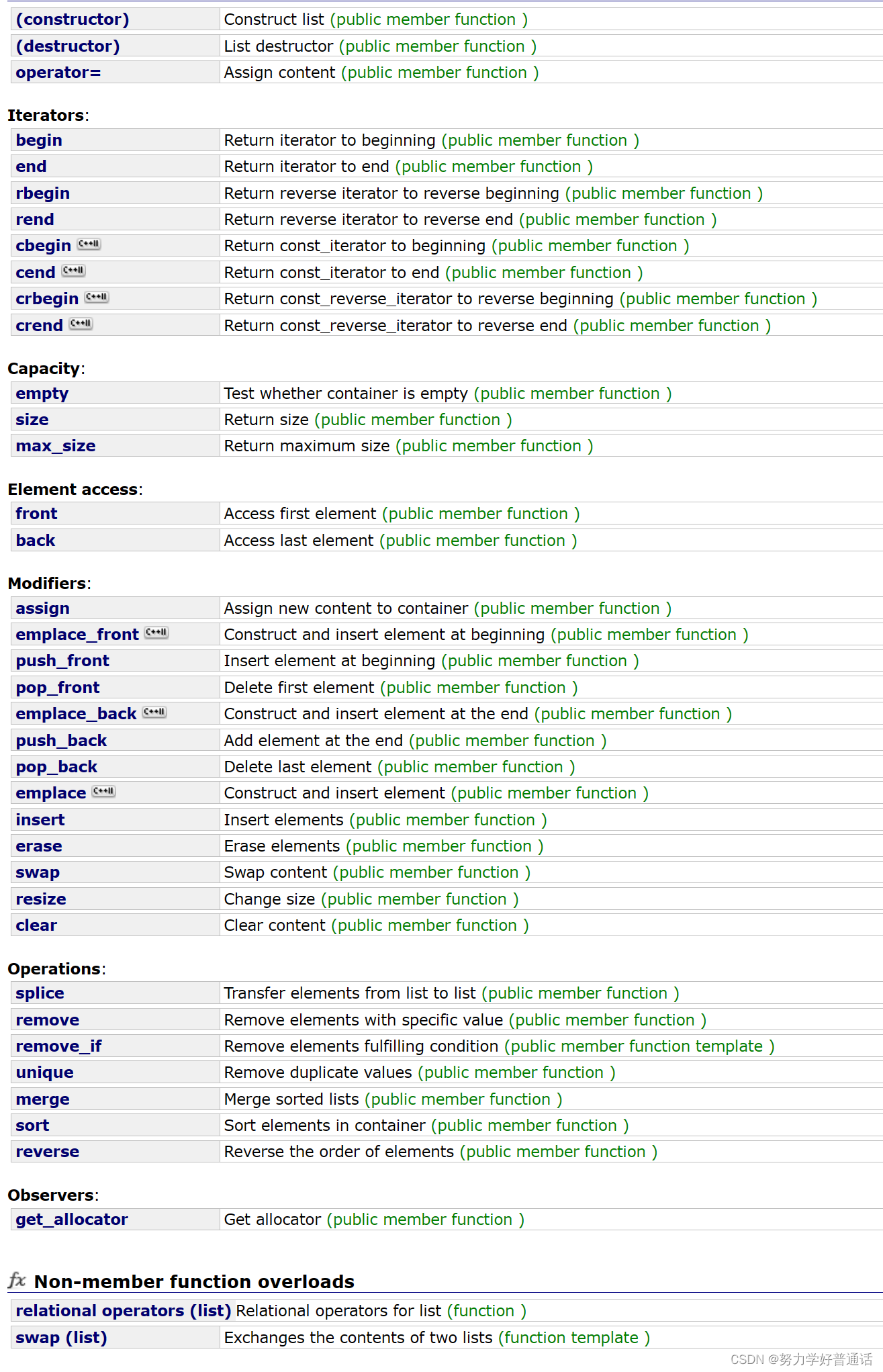
list使用
list的使用于string的使用都类似,首先通过查阅来看list有哪些函数: 可以看到函数还是蛮多的,我们值重点一些常用的和常见的: 1.关于push_back,push_front,和对应迭代器的使用 //关于push_back和push_front void test_list1() {l…...

【图解】多层感知器(MLP)
图片是一个多层感知器(MLP)的示意图,它是一种常见的神经网络模型,用于从输入到输出进行非线性映射。图片中的网络结构如下:...
React(8)
千锋学习视频https://www.bilibili.com/video/BV1dP4y1c7qd?p72&spm_id_frompageDriver&vd_sourcef07a5c4baae42e64ab4bebdd9f3cd1b3 1.React 路由 1.1 什么是路由? 路由是根据不同的 url 地址展示不同的内容或页面。 一个针对React而设计的路由解决方案…...

ssm社区管理与服务系统源码和论文
ssm社区管理与服务的设计与实现031 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 研究背景 当今时代是飞速发展的信息时代。在各行各业中离不开信息处理,这正是计算机被广泛应用于信息管理系统的…...
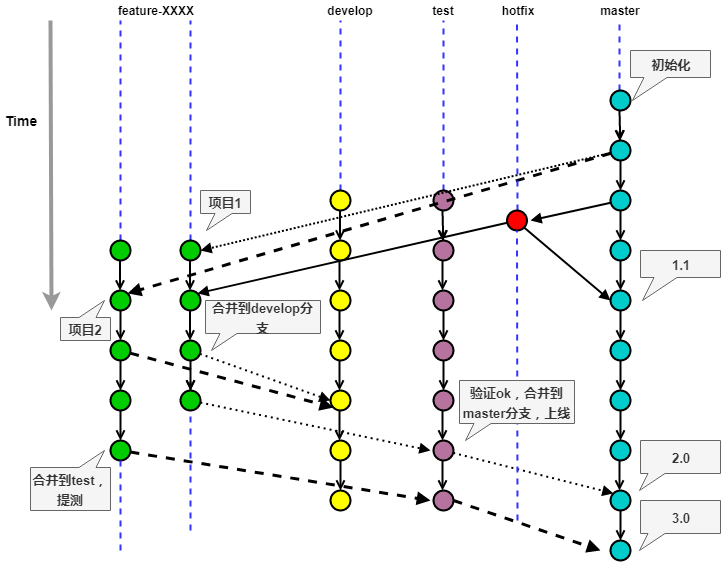
Git多版本并行开发实践
本文目的: 实现多个项目同时进行的git多版本管理工作流。 名词解释: feature-XXXX:特性分支指CCS中一个项目或者一个迭代,在该分支上开发,完成后,合并,最后,删除该分支,…...

修复hive重命名分区后新分区为0的问题
hive分区重命名后,新的分区的分区大小为0 , 例如 alter table entersv.ods_t_test partition(dt2022-11-08) rename to partition(dt2022-11-21) ods_t_test 的2022-11-21分区大小为0。怎样修复 使用 msck repair table 命令来修复表的元数据,让hive重新…...
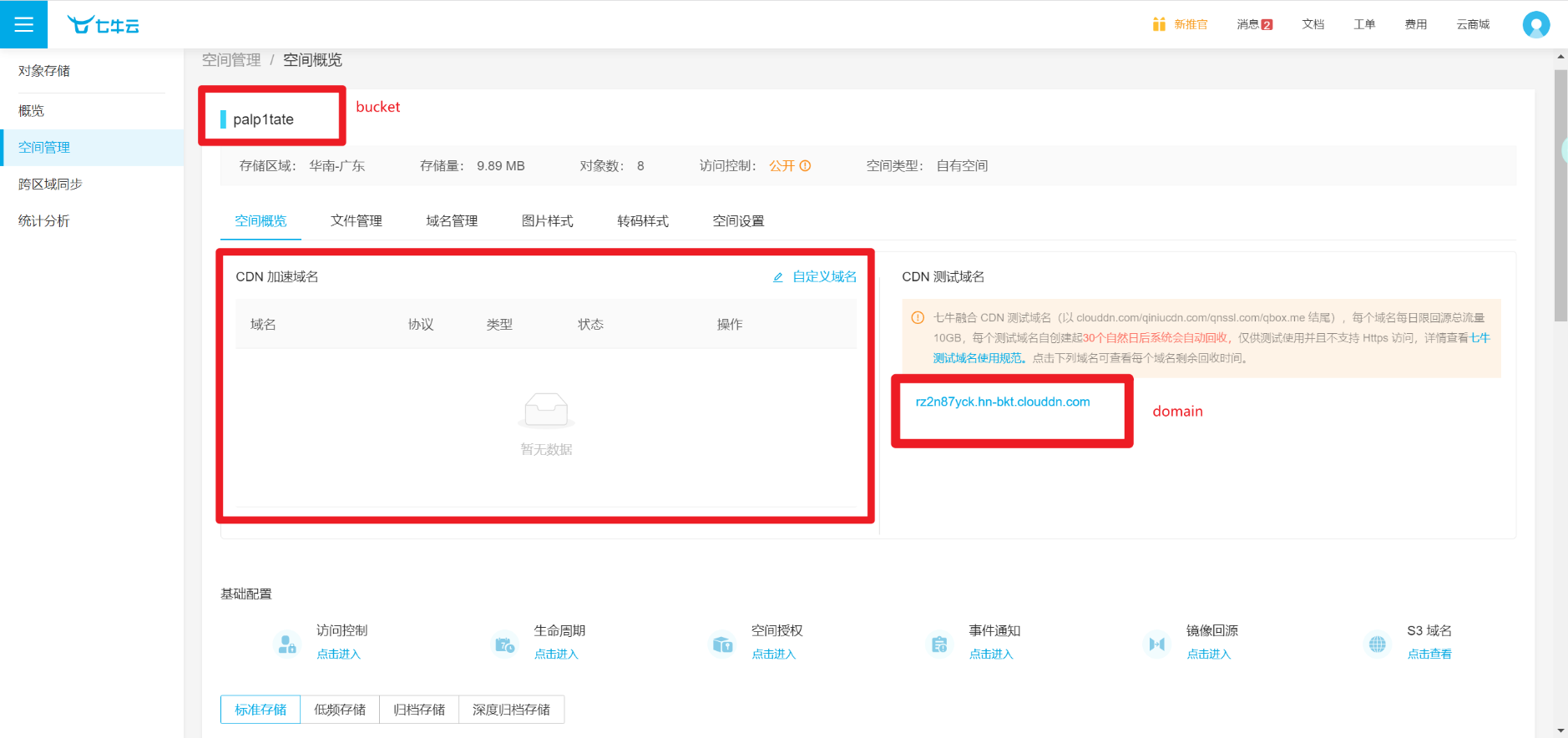
Gin+微服务实现抖音视频上传到七牛云
文章目录 安装获取凭证Gin处理微服务处理 如果你对Gin和微服务有一定了解,看本文较容易。 安装 执行命令: go get github.com/qiniu/go-sdk/v7获取凭证 Go SDK 的所有的功能,都需要合法的授权。授权凭证的签算需要七牛账号下的一对有效的A…...

go 连接操作MySQL
连接Mysql 访问此网站搜索MySQL第一个就是按照指引运行 go get -u github.com\go-sql-driver\mysql导入包建立连接 package mainimport ("database/sql""fmt""time"_ "github.com/go-sql-driver/mysql" )var db *sql.DBfunc initdb…...

git常见的命令,问题和处理方式
Git 是一个开源的分布式版本控制系统,用于敏捷高效地处理任何或小或大的项目。 Git 是 Linus Torvalds 为了帮助管理 Linux 内核开发而开发的一个开放源码的版本控制软件。 Git 与常用的版本控制工具 CVS, Subversion 等不同,它采用了分布式版本库的方…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
