第二章 搜索
本篇博文是笔者归纳汇总的AcWing基础课题集,方便读者后期复盘巩固~
PS:本篇文章只给出完整的算法实现,并没有讲解具体的算法思路。如果想看算法思路,可以阅读笔者往期写过的文章(或许会有),也可以移步AcWing官网看详情。
本篇文章的特点:每道题会给出多种解法,不局限于一种思路,可以帮助读者从不同角度思考题目。算法代码简洁,适合背诵记忆~~
Flood Fill
AcWing1097. 池塘计数
传送门
// 写法1:BFS
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
using PII = pair<int, int>;
#define x first
#define y second
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1}, dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
char g[N][N];
bool st[N][N];
PII q[N * N];
int n, m;void bfs(int sx, int sy) {int hh = 0, tt = 0;q[0] = {sx, sy};st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 8; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || g[a][b] == '.' || st[a][b]) continue;q[ ++ tt] = {a, b};st[a][b] = true;}}
}int main()
{cin >> n >> m;for (int i = 0; i < n; ++ i)for (int j = 0; j < m; ++ j)cin >> g[i][j];int ans = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (g[i][j] == 'W' && !st[i][j]) {bfs(i, j);++ ans;}}}printf("%d\n", ans);return 0;
}
// 写法2:DFS
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1}, dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
char g[N][N];
int n, m;void dfs(int x, int y) {char t = g[x][y];g[x][y] = '.';for (int i = 0; i < 8; ++ i) {int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || g[a][b] == '.') continue;dfs(a, b);}t = g[x][y]; // 这题貌似不需要恢复现场
}int main()
{cin >> n >> m;for (int i = 0; i < n; ++ i)for (int j = 0; j < m; ++ j)cin >> g[i][j];int ans = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (g[i][j] == 'W') {dfs(i, j);++ ans;}}}printf("%d\n", ans);return 0;
}
AcWing1098. 城堡问题
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 55;
#define x first
#define y second
using PII = pair<int, int>;
int dx[4] = {0, -1, 0, 1}, dy[4] = {-1, 0, 1, 0}; // 西、北、东、南
int g[N][N], n, m;
bool st[N][N];
PII q[N * N];int bfs(int sx, int sy) {int hh = 0, tt = 0, area = 0;q[0] = { sx,sy };st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) continue;// 取出某个数的第i个二进制位,然后与上1,如果结果为1,则表示有墙,如果为0,则表示没有墙// 比如11=1+2+8,它的二进制是1011,第0位为1,表示有西墙 第1位为1,表示有北墙// 第2位为0,表示没有东墙,第3位为1,表示有南墙if (g[t.x][t.y] >> i & 1) continue;q[ ++ tt] = {a, b};st[a][b] = true;}++ area;}return area;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; ++ i)for (int j = 0; j < m; ++ j)scanf("%d", &g[i][j]);int cnt = 0, area = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (!st[i][j]) {area = max(area, bfs(i, j));++ cnt;}}}printf("%d\n%d\n", cnt, area);return 0;
}
AcWing1106. 山峰和山谷
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
#define x first
#define y second
using PII = pair<int, int>;
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1}, dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
int h[N][N], n;
// has_higher是用来标记有没有比“当前(i,j)这个点所在的山脉”更高的山脉
// has_lower是用来标记有没有比“当前(i,j)这个点所在的山脉"更低的山脉
bool st[N][N], has_higher, has_lower;
PII q[N * N];void bfs(int sx, int sy) {int hh = 0, tt = 0;q[0] = {sx, sy};st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 8; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n) continue;if (h[a][b] != h[t.x][t.y]) {h[a][b] > h[t.x][t.y] ? has_higher = true : has_lower = true;} else {if (!st[a][b]) {q[ ++ tt] = {a, b};st[a][b] = true;}}}}
}int main()
{scanf("%d", &n);for (int i = 0; i < n; ++ i)for (int j = 0; j < n; ++ j)scanf("%d", &h[i][j]);int peak = 0, valley = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < n; ++ j) {if (!st[i][j]) {has_higher = has_lower = false;bfs(i, j);if (!has_higher) ++ peak;if (!has_lower) ++ valley;}}}printf("%d %d\n", peak, valley);return 0;
}
最短路模型
AcWing1076. 迷宫问题
传送门
// 逆向搜索
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
#define x first
#define y second
using PII = pair<int, int>;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
PII pre[N][N], q[N * N];
int g[N][N], n;
bool st[N][N];void bfs(int sx, int sy) {int hh = 0, tt = 0;q[0] = {sx, sy};st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n || g[a][b] || st[a][b]) continue;q[ ++ tt] = {a, b};st[a][b] = true;pre[a][b] = t;}}
}int main()
{scanf("%d", &n);for (int i = 0; i < n; ++ i)for (int j = 0; j < n; ++ j)scanf("%d", &g[i][j]);bfs(n - 1, n - 1); // 逆向搜索,即从终点搜索到起点PII p(0, 0);while (1) { // 正向打印“逆向搜索得到的路径” 从起点打印到终点printf("%d %d\n", p.x, p.y);if (p.x == n - 1 && p.y == n - 1) break;p = pre[p.x][p.y];}return 0;
}
// 正向搜索
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
#define x first
#define y second
using PII = pair<int, int>;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
PII pre[N][N], q[N * N];
int g[N][N], n;
bool st[N][N];void bfs(int sx, int sy) {int hh = 0, tt = 0;q[0] = {sx, sy};st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n || g[a][b] || st[a][b]) continue;q[ ++ tt] = {a, b};st[a][b] = true;pre[a][b] = t;}}
}void show(int a, int b) { // 类似于后序遍历// if (a || b) show(pre[a][b].x, pre[a][b].y);// printf("%d %d\n", a, b);// 等价于if (!a && !b) {puts("0 0");return ;}show(pre[a][b].x, pre[a][b].y);printf("%d %d\n", a, b);
}int main()
{scanf("%d", &n);for (int i = 0; i < n; ++ i)for (int j = 0; j < n; ++ j)scanf("%d", &g[i][j]);bfs(0, 0); // 正向搜索show(n - 1, n - 1); // 类似于后序遍历return 0;
}
AcWing188. 武士风度的牛
传送门
// 写法1:使用st[]判重数组
#include <bits/stdc++.h>
using namespace std;
const int N = 155;
#define x first
#define y second
using PII = pair<int, int>;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
int dist[N][N], n, m;
char g[N][N];
bool st[N][N];
PII q[N * N];int bfs(int sx, int sy) {memset(dist, -1, sizeof dist);int hh = 0, tt = 0;q[0] = {sx, sy};st[sx][sy] = true;dist[sx][sy] = 0;while (hh <= tt) {PII t = q[hh ++ ];// if (g[a][b] == 'H') return dist[t.x][t.y]; // 也可以在这里直接判断结果哦for (int i = 0; i < 8; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || st[a][b] || g[a][b] == '*') continue;if (g[a][b] == 'H') return dist[t.x][t.y] + 1;dist[a][b] = dist[t.x][t.y] + 1;q[++ tt] = {a, b};st[a][b] = true;}}return -1;
}int main()
{int sx, sy;scanf("%d%d", &m, &n);for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {cin >> g[i][j];if (g[i][j] == 'K') sx = i, sy = j; }}printf("%d\n", bfs(sx, sy));return 0;
}
// 写法2:如果dist[i]=-1则表示没有遍历过,可以用来代替st[]判重数组
#include <bits/stdc++.h>
using namespace std;
const int N = 155;
#define x first
#define y second
using PII = pair<int, int>;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
int dist[N][N], n, m;
char g[N][N];
PII q[N * N];int bfs(int sx, int sy) {memset(dist, -1, sizeof dist);int hh = 0, tt = 0;q[0] = {sx, sy};dist[sx][sy] = 0;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 8; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || ~dist[a][b] || g[a][b] == '*') continue;if (g[a][b] == 'H') return dist[t.x][t.y] + 1;dist[a][b] = dist[t.x][t.y] + 1;q[++ tt] = {a, b};}}return -1;
}int main()
{int sx, sy;scanf("%d%d", &m, &n);for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {cin >> g[i][j];if (g[i][j] == 'K') sx = i, sy = j; }}printf("%d\n", bfs(sx, sy));return 0;
}
AcWing1100. 抓住那头牛
传送门
// 写法1:使用st[]判重数组
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int dist[N], q[N], n, k;
bool st[N];int bfs() {memset(dist, -1, sizeof dist);int hh = 0, tt = 0;q[0] = n, dist[n] = 0;st[n] = true;while (hh <= tt) {int u = q[hh ++ ];if (u == k) return dist[u];if (u - 1 >= 0 && !st[u - 1]) {dist[u - 1] = dist[u] + 1;q[++ tt] = u - 1;st[u - 1] = true;}if (u + 1 < N && !st[u + 1]) {dist[u + 1] = dist[u] + 1;q[++ tt] = u + 1;st[u + 1] = true; }if (u * 2 < N && !st[2 * u]) {dist[2 * u] = dist[u] + 1;q[++ tt] = 2 * u;st[2 * u] = true;}}return -1;
}int main()
{scanf("%d%d", &n, &k);printf("%d\n", bfs());return 0;
}
// 写法2:如果dist[i]=-1则表示没有遍历过,可以用来代替st[]判重数组
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int dist[N], q[N], n, k;int bfs() {memset(dist, -1, sizeof dist);int hh = 0, tt = 0;q[0] = n, dist[n] = 0;while (hh <= tt) {int u = q[hh ++ ];if (u == k) return dist[u];if (u - 1 >= 0 && dist[u - 1] == -1) {dist[u - 1] = dist[u] + 1;q[++ tt] = u - 1;}if (u + 1 < N && dist[u + 1] == -1) {dist[u + 1] = dist[u] + 1;q[++ tt] = u + 1;}if (u * 2 < N && dist[2 * u] == -1) {dist[2 * u] = dist[u] + 1;q[++ tt] = 2 * u;}}return -1;
}int main()
{scanf("%d%d", &n, &k);printf("%d\n", bfs());return 0;
}
多源BFS
AcWing173 矩阵距离
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
#define x first
#define y second
using PII = pair<int, int>;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dist[N][N], n, m;
char g[N][N];
PII q[N * N];void bfs() {memset(dist, -1, sizeof dist);int hh = 0, tt = -1; // 注意:tt初始化为-1而不是0哦// 把所有字符'1'都放进队列中并且设定距离为0 其实就等价于// 从虚拟源点向这些起点连一条距离为0的边 但是我们并没有真的把虚拟源点建立出来for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (g[i][j] == '1') {dist[i][j] = 0; // 距离为0相当于 从虚拟源点向这些起点连一条距离为0的边q[++ tt] = {i, j}; // 将所有起点加入队列中}}}while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || ~dist[a][b]) continue;dist[a][b] = dist[t.x][t.y] + 1;q[++ tt] = {a, b};}}
}int main()
{cin >> n >> m;for (int i = 0; i < n; ++ i)for (int j = 0; j < m; ++ j)cin >> g[i][j];bfs();for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) printf("%d ", dist[i][j]);puts("");}return 0;
}
最小步数模型
AcWing1107. 魔板
传送门
#include <bits/stdc++.h>
#define x first
#define y second
using namespace std;
string op[3] = {"87654321", "41236785", "17245368"}; // 题意中这三种操作所对应的状态
// 外层的string表示当前状态
// pair中的char表示当前状态是由上一个状态经过哪种操作变换过来的, string表示上一个状态
unordered_map<string, pair<char, string>> pre;
// string表示当前状态的字符串 int表示到达当前状态所用的最短步骤数
unordered_map<string, int> dist;string move(string s, int i) { // 对状态s执行第i种操作string ans;// 类似于BFS中偏移数组dx,dy的那种思想for (int j = 0; j < 8; ++ j) ans += s[op[i][j] - '1'];return ans;
}int bfs(string S, string T) {if (S == T) return 0;queue<string> q;q.push(S);dist[S] = 0;while (q.size()) {string u = q.front(); q.pop();for (int i = 0; i < 3; ++ i) { // 枚举这三种操作string v = move(u, i);if (!dist.count(v)) {dist[v] = dist[u] + 1;pre[v] = {'A' + i, u};q.push(v);if (v == T) return dist[v];}}}return -1;
}int main()
{string S = "12345678", T;for (int i = 0, x; i < 8; ++ i) {cin >> x;T += x + '0';}int step = bfs(S, T);printf("%d\n", step);string ans;while (S != T) {ans += pre[T].x;T = pre[T].y;}reverse(ans.begin(), ans.end());if (step > 0) cout << ans << endl;return 0;
}
双端队列广搜
双端队列广搜又称为01BFS。
AcWing175. 电路维修
传送门
// 写法1:使用st判重数组
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
using PII = pair<int, int>;
#define x first
#define y second
// 某个点的左上、右上、右下、左下 四个方向的偏移量 注意哦:dx dy ix iy cs都是顺时针方向,即左上、右上、右下、左下
// 它们一定是要一一对应的,不能写错,不然for (int i = 0; i < 4; i++)枚举的时候所得到的dx,dy,ix,iy,cs都不是对应的,就会出错
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};
// 这里是定义四宫格中的电线所应该的标准的形式,即左上为\,右上为/,右下为\,左下为/
// 这样定义就可以让左上和右下直接相连,右上和左下直接相连,不用旋转,所以不需要花费代价
char cs[5] = "\\/\\/";
int dist[N][N], n, m, T;
bool st[N][N];
char g[N][N];int bfs() {memset(dist, 0x3f, sizeof dist);memset(st, 0, sizeof st);deque<PII> q;q.push_back({0, 0});dist[0][0] = 0;while (q.size()) {PII t = q.front(); q.pop_front();if (t.x == n && t.y == m) return dist[n][m];if (st[t.x][t.y]) continue; // 扩展过了,就直接跳过// 所有边的权重不同,所以某些点可能需要被扩展多次,即某个点可能多次入队// 这道题目可以看成是特殊的dijkstra算法,在dijkstra算法中,某些点可能会被多次扩展,// 但第一次从优先队列中弹出的节点的距离一定就是最小值了,所以需要在出队的时候来判重st[t.x][t.y] = true;for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a > n || b < 0 || b > m) continue;int u = t.x + ix[i], v = t.y + iy[i], w = (g[u][v] != cs[i]);if (dist[a][b] > dist[t.x][t.y] + w) {dist[a][b] = dist[t.x][t.y] + w;// w为0则插入到队头,w为1则插入到队尾w == 0 ? q.push_front({a, b}) : q.push_back({a, b});}}}return -1;
}int main()
{scanf("%d", &T);while (T -- ) {scanf("%d%d", &n, &m);for (int i = 0; i < n; ++ i) scanf("%s", g[i]);// n + m为奇数则无解if ((n + m) & 1) puts("NO SOLUTION");else printf("%d\n", bfs());}return 0;
}
// 写法2:不使用st判重数组,而且不需要说使用dist数组来替代st判重数组的含义,就可以完全直接省略st判重数组
/*这题只是有点特殊,这种做法并不适用于其他情况,大多数题目都需要st判重数组,而且可以使用dist数组来替代st判重数组的含义
只是对于01BFS的题目来说,可以这么写,完全省略st判重数组哦。
为什么01BFS可以直接省略st判重数组呢?
原因:其实01BFS使用了双端队列 (deque) 并结合了 Dijkstra 的思想,对于每个节点,只有当我们找到了一条到达该节点的更短路径时,我们才会将其放入队列中。
通过检查dist数组,我们实际上已经隐式地跟踪了这些信息:如果我们找到的新路径没有比当前记录在dist中的路径更短,
那么我们就可以忽略这个新路径,就像我们已经访问过这个节点一样。注意这里并不是说通过判断dist != INF来表达某个点是否已经访问过了,
而是通过比较dist大小更新路径的方式来隐式表达某个点是否已经访问过了。
但是请注意,去掉st判重数组可能会增加算法的运行时间,尤其是在那些存在许多冗余路径的图中。
这是一个具体的例子,这种方法可能并不适用于所有的 BFS 实现。
*/#include <bits/stdc++.h>
using namespace std;
const int N = 510;
using PII = pair<int, int>;
#define x first
#define y second
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};
char cs[5] = "\\/\\/";
int dist[N][N], n, m, T;
char g[N][N];int bfs() {memset(dist, 0x3f, sizeof dist);deque<PII> q;q.push_back({0, 0});dist[0][0] = 0;while (q.size()) {PII t = q.front(); q.pop_front();if (t.x == n && t.y == m) return dist[n][m];for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a > n || b < 0 || b > m) continue;int u = t.x + ix[i], v = t.y + iy[i], w = (g[u][v] != cs[i]);if (dist[a][b] > dist[t.x][t.y] + w) {dist[a][b] = dist[t.x][t.y] + w;w == 0 ? q.push_front({a, b}) : q.push_back({a, b});}}}return -1;
}int main()
{scanf("%d", &T);while (T -- ) {scanf("%d%d", &n, &m);for (int i = 0; i < n; ++ i) scanf("%s", g[i]);if ((n + m) & 1) puts("NO SOLUTION");else printf("%d\n", bfs());}return 0;
}
双向广搜
AcWing190. 字串变换
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 6;
string a[N], b[N], A, B;
int n;int extend(queue<string> &q, unordered_map<string, int> &da, unordered_map<string, int> &db, string a[], string b[]) {int d = da[q.front()]; // 按层扩展而不是按点扩展 把同一层中的所有元素都扩展完while (!q.empty() && da[q.front()] == d) {string u = q.front(); q.pop();for (int i = 0; i < n; ++ i) {for (int j = 0; j < u.size(); ++ j) {if (u.substr(j, a[i].size()) == a[i]) {string v = u.substr(0, j) + b[i] + u.substr(j + a[i].size());// 如果当前v这个字符串的状态在qa中已经被遍历过了,则跳过if (da.count(v)) continue;// 如果当前从起点开始搜索的v这个字符串的状态已经被"从终点开始搜索的"遍历过了//这说明v这个字符串就是"从起点开始搜索"和"从终点开始搜索"的相遇点//类似于打隧道,B已经打通了v,此时只要A打破v,那么就把隧道都打通了if (db.count(v)) return da[u] + 1 + db[v];da[v] = da[u] + 1;q.push(v);}}}}return 11;
}int bfs() {if (A == B) return 0;// 队列qa来存储从起点拓展的状态,队列qb存储从终点拓展的状态queue<string> qa, qb;// da表示从起点拓展到某一层用了多少步数 db表示从终点拓展到某一层用了多少步数unordered_map<string, int> da, db;qa.push(A), qb.push(B);da[A] = db[B] = 0;int step = 0;// 如果出现某个队列为空,说明这这两个队列没有交集,这个图不是连通的// 就跟打隧道一样,隧道为100米,A打通了40米就为停了,B打通了50米就为停了,那么还有10米,所以不可能打通while (!qa.empty() && !qb.empty()) {int t;// 这里有个优化就是要优先考虑队列中状态个数少的if (qa.size() < qb.size()) t = extend(qa, da, db, a, b);else t = extend(qb, db, da, b, a);if (t <= 10) return t;// step从0~9共10步,因此只要此时step=10则说明走了11步,不能在10步以内完成if (++ step == 10) return -1;}return -1;
}int main()
{cin >> A >> B;// 因为这里并没有明确告诉转换规则由多少个,所以需要根据输入的转换字符串来确定转换规则的个数while (cin >> a[n] >> b[n]) ++ n;int t = bfs();if (t == -1) puts("NO ANSWER!");else printf("%d\n", t);return 0;
}
A*
AcWing178. 第K短路
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 2e5 + 10;
#define x first
#define y second
using PII = pair<int, int>;
// 外层第一个int是f、pair中的第一个int是d+w[i](即g=d+w[i]), 第二个int是点的编号
using PIII = pair<int, pair<int, int>>;
int h[N], hs[N], e[M], ne[M], w[M], idx;
int dist[N], cnt[N], n, m, S, T, K;
bool st[N];void add(int h[], int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}void dijkstra() { // 求出从终点T到其他各点的最短距离,作为h()函数memset(dist, 0x3f, sizeof dist);dist[T] = 0;priority_queue<PII, vector<PII>, greater<PII>> q;q.push({0, T});while (q.size()) {PII t = q.top(); q.pop();int u = t.y;if (st[u]) continue;st[u] = true;for (int i = hs[u]; ~i; i = ne[i]) {int v = e[i];if (dist[v] > dist[u] + w[i]) {dist[v] = dist[u] + w[i];q.push({dist[v], v});}}}
}int A_star() {priority_queue<PIII, vector<PIII>, greater<PIII>> q;q.push({dist[S], {0, S}});while (q.size()) {PIII t = q.top(); q.pop();int u = t.y.y, d = t.y.x;++ cnt[u];if (cnt[T] == K) return d;for (int i = h[u]; ~i; i = ne[i]) {int v = e[i];if (cnt[v] < K) {// f() = g() + h(), 这里把g() = d + w[i], h() = dist[v]int f = d + w[i] + dist[v]; // 求出估价函数f()q.push({f, {d + w[i], v}});}}}return -1;
}int main()
{memset(h, -1, sizeof h), memset(hs, -1, sizeof hs);scanf("%d%d", &n, &m);while (m -- ) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(h, a, b, c), add(hs, b, a, c);}scanf("%d%d%d", &S, &T, &K);// 由于题目要求"每条最短路中至少要包含一条边"if (S == T) ++ K;dijkstra();printf("%d\n", A_star());return 0;
}
AcWing179 八数码
传送门
#include <bits/stdc++.h>
using namespace std;
using PIS = pair<int, string>;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
char op[4] = {'u', 'r', 'd', 'l'};
unordered_map<string, int> dist;
unordered_map<string, pair<string, char>> pre;
string S, T = "12345678x";int get(string s) {int ans = 0;for (int i = 0; i < s.size(); ++ i) {if (s[i] != 'x') {int t = s[i] - '1';ans += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);}}return ans;
}void bfs() {priority_queue<PIS, vector<PIS>, greater<PIS>> q;q.push({get(S), S});dist[S] = 0;while (q.size()) {auto t = q.top(); q.pop();string s = t.second;if (s == T) break;int d = dist[s], x, y;for (int i = 0; i < s.size(); i ++ ) {if (s[i] == 'x') {x = i / 3, y = i % 3;break;}}string str = s;for (int i = 0; i < 4; ++ i) {int a = x + dx[i], b = y + dy[i];if (a >= 0 && a < 3 && b >= 0 && b < 3) {swap(s[x * 3 + y], s[a * 3 + b]);if (!dist.count(s) || dist[s] > d + 1) {dist[s] = d + 1;pre[s] = {str, op[i]};q.push({dist[s] + get(s), s});}swap(s[x * 3 + y], s[a * 3 + b]);}}}
}int main()
{string c, seq;while (cin >> c) {S += c;if (c != "x") seq += c;}int cnt = 0;for (int i = 0; i < seq.size(); ++ i)for (int j = i + 1; j < seq.size(); ++ j)if (seq[i] > seq[j])++ cnt;if (cnt & 1) puts("unsolvable");else {bfs();string ans;while (S != T) {ans += pre[T].second;T = pre[T].first;}reverse(ans.begin(), ans.end());cout << ans << endl;}return 0;
}
DFS之连通性模型
AcWing1112. 迷宫
传送门
// DFS
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
char g[N][N];
bool st[N][N];
int n, T, sx, sy, ex, ey;bool dfs(int x, int y) {if (g[x][y] == '#') return false;if (x == ex && y == ey) return true;st[x][y] = true;for (int i = 0; i < 4; ++ i) {int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n || st[a][b]) continue;if (dfs(a, b)) return true;}return false;
}int main()
{scanf("%d", &T);while (T -- ) {memset(st, 0, sizeof st);scanf("%d", &n);for (int i = 0; i < n; ++ i) scanf("%s", g[i]);scanf("%d%d%d%d", &sx, &sy, &ex, &ey);if (g[sx][sy] == '#' || g[ex][ey] == '#') {puts("NO");continue;}puts(dfs(sx, sy) ? "YES" : "NO");}return 0;
}
// BFS
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
#define x first
#define y second
using PII = pair<int, int>;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
char g[N][N];
bool st[N][N];
PII q[N * N];
int n, T, sx, sy, ex, ey;bool bfs() {memset(st, 0, sizeof st);int hh = 0, tt = 0;q[0] = {sx, sy};st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];if (t.x == ex && t.y == ey) return true;for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= n || g[a][b] == '#' || st[a][b]) continue;q[++ tt] = {a, b};st[a][b] = true;}}return false;
}int main()
{scanf("%d", &T);while (T -- ) {scanf("%d", &n);for (int i = 0; i < n; ++ i) scanf("%s", g[i]);scanf("%d%d%d%d", &sx, &sy, &ex, &ey);if (g[sx][sy] == '#' || g[ex][ey] == '#') {puts("NO");continue;}puts(bfs() ? "YES" : "NO");}return 0;
}
AcWing1113. 红与黑
传送门
// DFS
#include <bits/stdc++.h>
using namespace std;
const int N = 25;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
char g[N][N];
bool st[N][N];
int n, m;int dfs(int x, int y) {int cnt = 1;st[x][y] = true;for (int i = 0; i < 4; ++ i) {int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || st[a][b] || g[a][b] != '.') continue;cnt += dfs(a, b);}return cnt;
}int main()
{while (~scanf("%d%d", &m, &n), m || n) {memset(st, 0, sizeof st);for (int i = 0; i < n; ++ i) scanf("%s", g[i]);int sx, sy;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (g[i][j] == '@') {sx = i, sy = j;break;}}}printf("%d\n", dfs(sx, sy));}return 0;
}
// BFS
#include <bits/stdc++.h>
using namespace std;
const int N = 25;
#define x first
#define y second
using PII = pair<int, int>;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
char g[N][N];
bool st[N][N];
PII q[N * N];
int n, m;int bfs(int sx, int sy) {int hh = 0, tt = 0, cnt = 1;q[0] = {sx, sy};st[sx][sy] = true;while (hh <= tt) {PII t = q[hh ++ ];for (int i = 0; i < 4; ++ i) {int a = t.x + dx[i], b = t.y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || st[a][b] || g[a][b] != '.') continue;++ cnt;q[ ++ tt] = {a, b};st[a][b] = true;}}return cnt;
}int main()
{while (~scanf("%d%d", &m, &n), m || n) {memset(st, 0, sizeof st);for (int i = 0; i < n; ++ i) scanf("%s", g[i]);int sx, sy;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (g[i][j] == '@') {sx = i, sy = j;break;}}}printf("%d\n", bfs(sx, sy));}return 0;
}
DFS之搜索顺序
AcWing1116. 马走日
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 10;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2}, dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
bool st[N][N];
int n, m, sx, sy, ans, T;void dfs(int x, int y, int cnt) {if (cnt == n * m) {++ ans;return ;}st[x][y] = true;for (int i = 0; i < 8; ++ i) {int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) continue;dfs(a, b, cnt + 1);}st[x][y] = false;
}int main()
{scanf("%d", &T);while (T -- ) {ans = 0;memset(st, 0, sizeof st);scanf("%d%d%d%d", &n, &m, &sx, &sy);dfs(sx, sy, 1);printf("%d\n", ans);}return 0;
}
AcWing1117 单词接龙
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 25;
int g[N][N], used[N], ans, n;
string words[N];void dfs(string dragon, int last) {ans = max(ans, (int)dragon.size());++ used[last];for (int i = 0; i < n; ++ i) if (g[last][i] > 0 && used[i] < 2) dfs(dragon + words[i].substr(g[last][i]), i);-- used[last];
}int main()
{scanf("%d", &n);for (int i = 0; i < n; ++ i) cin >> words[i];char c;cin >> c;for (int i = 0; i < n; ++ i) {for (int j = 0; j < n; ++ j) {string a = words[i], b = words[j];int lenA = a.size(), lenB = b.size();for (int k = 1; k < min(lenA, lenB); ++ k) {if (a.substr(lenA - k, k) == b.substr(0, k)) {g[i][j] = k;break;}}}}for (int i = 0; i < n; ++ i)if (words[i][0] == c)dfs(words[i], i);printf("%d\n", ans);return 0;
}
AcWing1118. 分成互质组
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 12;
// group数组其实它存储的是原序列中某个数的下标
// group[i][j]=pos表示第i组中下标为j的那个数的位置,它在原序列中的下标是pos
int group[N][N],p[N], n, ans = N;
// 判断原序列中的某个数是否已经被分好组了
bool st[N];inline int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}// check一下p[i]这个数是否与gp这个组内的数数互质
bool check(int gp[], int gc, int i) {for (int j = 0; j < gc; ++ j)if (gcd(p[gp[j]], p[i]) != 1)return false;return true;
}// 参数g表示第g组,gc表示第g组内的当前枚举到的下标,tc表示到目前为止所有组中一共有多少个元素了
// start表示从原序列的哪个下标开始枚举
void dfs(int g, int gc, int tc, int start) {if (g >= ans) return ;if (tc == n) {ans = g;return ;}bool ok = true; // 判断是否需要新开一个组,初始时true表示需要新开一个组for (int i = start; i < n; ++ i) {// 如果下标i所对应的原序列中的那个数还没有被分好组并且当我们想要把这个数放入第g组时// 并且它与第g中的所有数字互质if (!st[i] && check(group[g], gc, i)) {st[i] = true; // 下标i所对应的原序列中的那个数已经被分好组了// 第g组中下标gc所指向的东西是原序列中刚加入这个组的那个数的下标group[g][gc] = i;dfs(g, gc + 1, tc + 1, i + 1);// 恢复现场st[i] = false;ok = false;}}// 表示需要新开一个组if (ok) dfs(g + 1, 0, tc, 0);
}int main()
{scanf("%d", &n);for (int i = 0; i < n; ++ i) scanf("%d", &p[i]);dfs(1, 0, 0, 0);printf("%d\n", ans);return 0;
}
DFS之剪枝与优化
AcWing165 小猫爬山
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int c[N], bus[N], n, w, ans = N;void dfs(int u, int cnt) {// 最优性剪枝if (cnt >= ans) return ;if (u > n) {ans = min(ans, cnt);return ;}// 对于第u只小猫,我们先遍历之前已经租用的这cnt辆缆车,看看它能被放入哪一辆车中// 如果都不能放进入,则说明需要新开一辆缆车来安置这只小猫for (int i = 1; i <= cnt; ++ i) {if (bus[i] + c[u] <= w) {bus[i] += c[u];dfs(u + 1, cnt);bus[i] -= c[u];}}// 新开一辆车bus[++ cnt] = c[u];dfs(u + 1, cnt);bus[cnt] = 0;
}int main()
{scanf("%d%d", &n, &w);for (int i = 1; i <= n; ++ i) scanf("%d", &c[i]);// 可行性剪枝:重量从大到小排序sort(c + 1, c + 1 + n, greater<int>()); dfs(1, 0);printf("%d\n", ans);return 0;
}
AcWing166 数独
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 9;
int ones[1 << N], mp[1 << N];
int row[N], col[N], cell[3][3];
char s[100];inline int lowbit(int x) {return x & -x;
}void init() {for (int i = 0; i < N; ++ i) row[i] = col[i] = (1 << N) - 1;for (int i = 0; i < 3; ++ i)for (int j = 0; j < 3; ++ j)cell[i][j] = (1 << N) - 1;
}// 获取行、列、小的九宫格的交集的方案数 比如最终结果为100101010,则表示整数2、4、6、9还可以用
inline int get(int x, int y) {return row[x] & col[y] & cell[x / 3][y / 3];
}bool dfs(int cnt) {if (!cnt) return true;int x, y, minv = 10; // minv记录最少的二进制中1的个数(因为1的个数越少,说明状态数更少)for (int i = 0; i < N; ++ i) {for (int j = 0; j < N; ++ j) {if (s[i * 9 + j] == '.') {int t = ones[get(i, j)]; // 查询100101010有多少个1 if (t < minv) {minv = t;x = i, y = j;}}}}// 依次枚举(x,y)这个格子可以填的数 比如010010000则表示(x,y)这个格子可以填5和8for (int i = get(x, y); i; i -= lowbit(i)) {int t = mp[lowbit(i)]; // 经过lowbit运算后,还需要进一步mp// 开始填数,修改状态row[x] -= 1 << t;col[y] -= 1 << t;cell[x / 3][y / 3] -= 1 << t;s[x * 9 + y] = t + '1';// 未填位置少1,继续递归下一个空位if (dfs(cnt - 1)) return true;// 恢复现场row[x] += 1 << t;col[y] += 1 << t;cell[x / 3][y / 3] += 1 << t;s[x * 9 + y] = '.';}return false;
}int main()
{for (int i = 0; i < N; ++ i) mp[1 << i] = i;for (int i = 0; i < 1 << N; ++ i)for (int j = 0; j < N; ++ j)ones[i] += i >> j & 1;while (cin >> s, s[0] != 'e') {init();int cnt = 0; // cnt表示当前有多少个空位需要填写// 把原序列输入的东西,转换到数独地图中,处理好预局面for (int i = 0, u = 0; i < N; ++ i) {for (int j = 0; j < N; ++ j, ++ u) {if (s[u] != '.') {int t = s[u] - '1';// 填入数字到数独地图中row[i] -= 1 << t;col[j] -= 1 << t;cell[i / 3][j / 3] -= 1 << t;}else {++ cnt;}}}dfs(cnt);cout << s << endl;}return 0;
}
AcWing167. 木棒
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 70;
int c[N], n, s, per;
bool used[N]; // 标记某根小木棍是否已经被使用过了// u表示当前枚举的是第u组
// len表示当前枚举的第u组原始木棒时,这个木棒里面的那些已经拼凑好的木棍长度之和是len
// start表示枚举第u根原始木棒时 这个木棒中拼凑的起始木棍编号
bool dfs(int u, int len, int start) {// 有u组,每组内的木棍长度是per 如果u * per = s, 则找到一个合法解perif (u * per == s) return true;// 第u组已经处理完毕,继续去处理第u+1组if (len == per) return dfs(u + 1, 0, 0);for (int i = start; i < n; ++ i) {if (used[i] || len + c[i] > per) continue;used[i] = true;if (dfs(u, len + c[i], i + 1)) return true;used[i] = false;// len==0表示拼凑第一根小木棍就失败了// len+w[i]==per表示拼凑最后一根小木棍失败了if (!len || len + c[i] == per) return false;int j = i;// 如果把i这根小木棍放进这个模拟的原始木棒中不合法 那么就跳过所有木棍长度与i相等的木棍while (j < n && c[j] == c[i]) ++ j;i = j - 1;}return false;
}int main()
{while (~scanf("%d", &n), n) {memset(used, 0, sizeof used);s = 0;for (int i = 0; i < n; ++ i) {scanf("%d", &c[i]);s += c[i];}sort(c, c + n, greater<int>());per = 1;while (1) {if (s % per == 0 && dfs(0, 0, 0)) {printf("%d\n", per);break;}++ per;}}return 0;
}
AcWing168 生日蛋糕
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 25, INF = 0x3f3f3f3f;
int minv[N], mins[N], R[N], H[N], n, m, ans = INF;// u表示当前层 sumv记录的是第m层到第u-1层的体积和(不包括第u层的体积 因为它还没有被处理出来)
// sums记录的是第m层到第u-1层的面积和(不包括第u层的体积 因为它还没有被处理出来)
void dfs(int u,int sumv,int sums) {// u=0表示第0层 说明第m层到第1层的蛋糕都已经被处理完了// 既然这m层蛋糕都处理完了 那么就可以记录最优解if(!u) {if (sumv == n && sums < ans) ans=sums;return; }// 剪枝1:当前体积和 + 剩余上面几层的最小体积和 > 总体积n 则回溯退出if (sumv + minv[u] > n) return;// 剪枝2:当前面积和 + 剩余上面几层的最小面积和 >= 最优解ans 则回溯退出if (sums + mins[u] >= ans) return;// 剪枝3:当前面积和 + 剩余面积(根据剩余体积进行公式换算) >= 最优解ans 则回溯退出if(sums + 2 * (n - sumv) / R[u + 1] >= ans) return;// 当前层的半径r的取值范围是[ u , min(R[u+1]-1,(int)sqrt((n-sumv-minv[u-1])/u)) ]for (int r = min(R[u + 1] - 1, (int)sqrt((n - sumv - minv[u - 1]) / u)); r >= u; -- r) {//当前层的高度h的取值范围是[ u , min(H[u+1]-1,(int)((n-sumv-minv[u-1])/(r*r))) ]for (int h = min(H[u + 1] - 1, (int)((n - sumv - minv[u - 1]) / (r * r))); h >=u ; -- h) {int t = 0; // t记录的底面积// 如果当前层是最底层 即第m层 那么就可以计算出所有层的上表面积其实就等于第m层的底面积if (u == m) t = r * r;R[u] = r, H[u] = h; // 记录第u层的半径和高度// 递归第u-1层 sumv+r*r*h是第m层到第u层的体积和(包括了第u层)// sums+2*r*h+t是第m层到第u层的面积和(包括了第u层) // 题目要求的面积=侧面积2*r*h+上表面积t 如果是第m层则t=r*r 否则t=0dfs(u - 1, sumv + r * r * h, sums + 2 * r * h + t);}}
}int main()
{scanf("%d%d", &n, &m);// 预处理出前i层的最小体积和 前i层的最小面积和(严格来说是最小侧面积和 而不包括上表面积和)for (int i = 1; i <= m; ++ i) {minv[i] = minv[i - 1] + i * i * i;mins[i] = mins[i - 1] + 2 *i *i;}// 由于我们再式子中会用到min(R[u+1]) m+1层不存在,作为哨兵,减少边界情况的判断 R[m + 1] = H[m + 1] = INF;// 从最底层第m层开始深搜dfs(m, 0, 0);if (ans == INF) puts("0");else printf("%d\n", ans);return 0;
}
迭代加深
AcWing170. 加成序列
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int path[N], n, maxDep;bool dfs(int dep) {if (dep > maxDep) return false;if (path[dep - 1] == n) return true;// 如果在当前深度depth搜索不到答案时,就继续到下一个深度depth+1去搜索,但是进入下一个深度时// 我们是又从第1层搜索到了第depth+1层,每次进入下一层depth+1时,都要把st数组清空// 不然上一层depth它搜索的过程从第1层到第depth层中的st数组的数据还会保留// 那么就会影响到下一层depth+1它搜索的过程从第1层到第depth+1层的st数组的数据了// 优化性剪枝1:去重// 用来判断某个求和的数是否被多次计算,判重,比如1 2 3 4,1+4=5和2+3=5,那么5就会被计算2次bool st[N] = {0};// 优化性剪枝2:优先从大到小的数枚举,因为从更大的数枚举更容易逼近n,分支数更少for (int i = dep - 1; i >= 0; -- i) {for (int j = i; j >= 0; -- j) {int s = path[i] + path[j];if (s > n || s <= path[dep - 1] || st[s]) continue;path[dep] = s;st[s] = true;if (dfs(dep + 1)) return true;}}return false;
}int main()
{path[0] = 1; // 整数1是固定会有的,所以让path[0]=1while (~scanf("%d", &n), n) {maxDep = 1; // 因为path[0]=1,即整数1这个数已经占据了一层深度,所以初始maxDep=1// 如果当前的这一层没有找到合法但,则继续去寻找下一层while (!dfs(1)) ++ maxDep;for (int i = 0; i < maxDep; ++ i) printf("%d ", path[i]);puts("");}return 0;
}
双向DFS
AcWing171. 送礼物
传送门
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
// w数组用来存储一个集合中所有物品的可能取得到的重量
int g[50], w[1 << 25], n, m, k, ans, cnt;void dfs1(int u, int s) {if (u == k) {w[cnt ++ ] = s;return;}if ((LL)s + g[u] <= m) dfs1(u + 1, s + g[u]);dfs1(u + 1, s);
}void dfs2(int u, int s) {if (u == n) {int l = 0, r = cnt - 1;while (l < r) {int mid = l + r + 1 >> 1;if (w[mid] + (LL)s <= m) l = mid;else r = mid - 1;}if (w[l] + (LL)s <= m) ans = max(ans, w[l] + s);return;}if ((LL)s + g[u] <= m) dfs2(u + 1, s + g[u]);dfs2(u + 1, s);
}int main()
{scanf("%d%d", &m, &n);for (int i = 0; i < n; ++ i) scanf("%d", &g[i]);sort(g, g + n, greater<int>());k = n / 2 + 2; // 防止 n = 1时,出现死循环dfs1(0, 0);sort(w, w + cnt);cnt = unique(w, w + cnt) - w;dfs2(k, 0);printf("%d\n", ans);return 0;
}
IDA*
AcWing180 排书
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 20;
// q[]书的排列, w[][]4步以内书的排列
int q[N], w[5][N], n, T, maxDep; // 估价函数
int get() {int cnt = 0; // 错误后继的数量for (int i = 0; i < n - 1; ++ i) if (q[i + 1] != q[i] + 1)++ cnt;// cnt/3向上取整的 写法 是(cnt+2)/3return (cnt + 2) / 3;
}// 迭代加深 dep是当前层 maxDep是深度限制
bool dfs(int dep) {// 超过最大深度限制 则立即回溯if (dep + get() > maxDep) return false;//估价函数为0 则到达了目标状态if (get() == 0) return true;// 这里有点类似于区间DPfor (int len = 1; len <= n; ++ len) { // 枚举抽取其中连续的一段的长度for (int l = 0; l + len - 1 < n; ++ l) { // 枚举抽取的这段书的左端点int r = l + len - 1; // r是抽取的这段书的右端点for (int j = r + 1; j < n; ++ j) { // 枚举抽取的这段书应该插入到r后面的哪个位置memcpy(w[dep], q, sizeof q); // 先记录之前的状态int k = l;for (int x = r + 1; x <= j; ++ x) q[k ++] = w[dep][x];for (int x = l; x <= r; ++ x) q[k ++] = w[dep][x];// 向下一层递归if (dfs(dep + 1)) return true;memcpy(q, w[dep], sizeof q); // 恢复之前的状态 恢复现场}}}// 搜完全部都搜不到 无解return false;
}int main()
{scanf("%d", &T);while(T --) {scanf("%d", &n);for (int i = 0; i < n; ++ i) scanf("%d", &q[i]);maxDep = 0; // 最大深度限制while (maxDep < 5 && !dfs(0)) ++ maxDep;if (maxDep >= 5) puts("5 or more");else printf("%d\n", maxDep);}return 0;
}
AcWing181 回转游戏
传送门
#include <bits/stdc++.h>
using namespace std;
const int N = 30;
// 给图形中的每个方格一个标号
int op[8][7] = {{0, 2, 6, 11, 15, 20, 22},{1, 3, 8, 12, 17, 21, 23},{10, 9, 8, 7, 6, 5, 4},{19, 18, 17, 16, 15, 14, 13},{23, 21, 17, 12, 8, 3, 1},{22, 20, 15, 11, 6, 2, 0},{13, 14, 15, 16, 17, 18, 19},{4, 5, 6, 7, 8, 9, 10}
};
// 将A到H的操作都编号为0到7, opposite[0]=5 表示0的相反操作是5
int opposite[8] = {5, 4, 7, 6, 1, 0, 3, 2};
// 中间8个格子的编号
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};
// q[]记录题目中输入的数字, path[]记录方案
int q[N], path[100], maxDep; // 计算估价函数
int get() {int sum[4] = {0};for (int i = 0; i < 8; ++ i) {int x = center[i];++ sum[q[x]];}int k = 0; // 找到中间8个方格中出现次数最多的那个数// 方格中的数字只能是1 2 3for (int i = 1; i <= 3; ++ i) k = max(k, sum[i]);return 8 - k;
}// 循环移动的操作
void operate(int x) {int t = q[op[x][0]];for (int i = 0; i < 6; ++ i) q[op[x][i]] = q[op[x][i + 1]];q[op[x][6]] = t;
}// 迭代加深 dep是当前搜索层 maxDep是深度限制 last是上一次的操作
bool dfs(int dep, int last) {if (dep + get() > maxDep) return false;if (get() == 0) return true;// 依次按照字典序枚举A到H这8种操作for (int i = 0; i < 8; ++ i) {// 当前i这个操作的逆向操作不等于上一次的操作if (opposite[i] != last) {operate(i); // 执行i操作path[dep] = i; // 记录当前层的操作是iif (dfs(dep+1, i)) return true;// 恢复现场path[dep] = 0;operate(opposite[i]);}}return false;
}int main()
{while(cin >> q[0], q[0]) {for (int i = 1;i < 24; ++ i) scanf("%d",&q[i]);maxDep = 0; // 最大深度限制while (!dfs(0, -1)) ++ maxDep;if (!maxDep) printf("No moves needed");else {for (int i = 0; i < maxDep; ++ i) printf("%c",'A' + path[i]);}// 最中间的8个格子最终都是相同的 编号是从6开始 那么输出q[6]即可printf("\n%d\n", q[6]);}return 0;
}
相关文章:

第二章 搜索
本篇博文是笔者归纳汇总的AcWing基础课题集,方便读者后期复盘巩固~ PS:本篇文章只给出完整的算法实现,并没有讲解具体的算法思路。如果想看算法思路,可以阅读笔者往期写过的文章(或许会有),也可…...

transform_train.json文件解析
transform_train.json 文件内容解析transform_matrix 文件内容解析 {"camera_angle_x": 0.6911112070083618,"frames": [{"file_path": "./train/r_0","rotation": 0.012566370614359171,"transform_matrix": [[…...
Wlan——锐捷零漫游网络解决方案以及相关配置
目录 零漫游介绍 一代零漫游 二代单频率零漫游 二代双频率零漫游 锐捷零漫游方案总结 锐捷零漫游方案的配置 配置无线信号的信道 开启关闭5G零漫游 查看配置 零漫游介绍 普通的漫游和零漫游的区别 普通漫游 漫游是由一个AP到另一个AP或者一个射频卡到另一个射频卡的漫…...

分布式锁系列之zookeeper分布式锁和mysql分布式锁
目录 介绍 下载安装 基本指令编辑 java集成zookeeper 官方提供版 永久节点 临时节点编辑 永久序列化节点 判断当前节点是否存在 获取当前节点中的数据内容 获取当前节点的子节点 更新节点内容 删除节点 zookeeper实现分布式锁 Mysql实现分布式锁 总结 介绍 ZooK…...

Ubuntu部署PHP7.4
系统版本:Ubuntu22.04 PHP版本: 7.4 Mysql版本:8.0 Nginx版本: 最新 1. 更新系统 首先,确保系统包是最新的: sudo apt update && sudo apt upgrade -y2. 安装 Nginx Nginx 在默认的 Ubuntu 仓库中,因此安装…...
WPF中的数据转换-StringFormat
WPF中的数据转换-StringFormat 前言 字符串格式化。使用该功能可以通过设置Binding.StringFormat属性对文本形式的数据进行转换——例如包含日期和数字的字符串。对于至少一半的格式化任务,字符串格式化是一种便捷的技术。 使用 当设置Binding.StringFormat属性…...

java.lang.UnsupportedOperationException解决方法
java.lang.UnsupportedOperationException解决方法 先放错误信息业务场景报错分析先看报错代码位置进入源码查看至此 真相大白 解决方法总结 先放错误信息 业务场景 已知有学生 张三李四王五赵六 等人 private List<String> nameList Arrays.asList("张三", &…...
docker for window更改到非系统盘的使用记录
1、使用Hyper-v模式的docker安装 2、安装docker for windows后安装目录没办法自己选择,固定在c盘 卸载后通过命令行方式设置软连接方式后重新安装来让其安装到软连接的d盘,解决c盘空间问题 mklink /j "C:\Program Files\Docker" "D:\Pr…...

day 38 | ● 518. 零钱兑换 II ● 377. 组合总和 Ⅳ
518. 零钱兑换 II 这道题就是完全背包问题,因为可以选择的数量是无限的。所以第二层的遍历顺序就是从前往后。 因为是次数问题,递推公式是 的,初值应该设定为dp【0】 1,否则无法进行累加。 func change(amount int, coins []i…...

写得了代码,焊得了板!嵌入式开发工程师必修之代码管理方案(中)
目录 2.2 分仓、权限与依赖问题 2.3 基于 Git 进行多仓管理 Git submodule Git subtree Script/CMake Git-Repo Conan 本文来自 武让 极狐GitLab 高级解决方案架构师 🌟 前一篇文章,作者介绍了嵌入式开发场景的代码管理特点与诉求,以及…...

Interlij IDEA 运行 ruoyi 后端项目。错误: 找不到或无法加载主类 com.ruoyi.auth.RuoYiAuthApplication
错误: 找不到或无法加载主类 com.ruoyi.auth.RuoYiAuthApplication 用了 IDEA运行,参考以下issue删除.idea目录也没有用 (官方文档写是用Eclipse运行) 错误: 找不到或无法加载主类 com.ruoyi.auth.RuoYiAuthApplication Issue #I48N2X 若依/RuoYi-C…...

相机设置报错记录
Camera->SetPosition(0.0, -980, 0.0);Camera->SetFocalPoint(0.0, 0.0, 0.0);Camera->SetViewUp(0.0, 1.0, 0.0);上述代码出现错误提示Resetting view-up since view plane normal is parallel,这个时候是viewup方向与投影方向平行了,而出现的…...

Vue3中搜索表单的二次封装
最近使用Vue3ElementPlus开发项目,从整体上构思组件的封装。能写成组件的内容都进行封装,方便多个地方使用。 受AntDesign的启发,在项目中有搜索表单table分页的地方可以封装为一个组件,只需要对组件传入table的列,组成…...

百度23Q2财报最新发布:营收利润加速增长,AI+生态战略渐显规模
百度集团-SW(9888.HK)Q2财报已于2023/08/22(美东)盘前发布,二季度百度集团整体收入实现341亿元,同比增长15%;归属百度的净利润(non-GAAP)达到80亿元,同比增长44%。营收和利润双双实现大幅增长,超市场预期。其中,百度核…...

一个pdf文件分割成两个
# -- coding: utf-8 --** import PyPDF2 # 打开原始PDF文件 # with open(zhongguojinxiandaishi.pdf, rb) as pdf_file: # pdf_reader PyPDF2.PdfReader(pdf_file) # num_pages len(pdf_reader.pages) # # # 确定分割点(例如,将页面一分为二࿰…...

Android 保存图片
这个主要讲的InputStream去保存。 如果需要BItmap与InputStream相互转换可以参考 Android Bitmap、InputStream、Drawable、byte[]、Base64之间的转换关系 保存图片我们需要考虑系统版本,Q前后还是不一样的。 /*** 保存图片* param context 上下文* param inputS…...
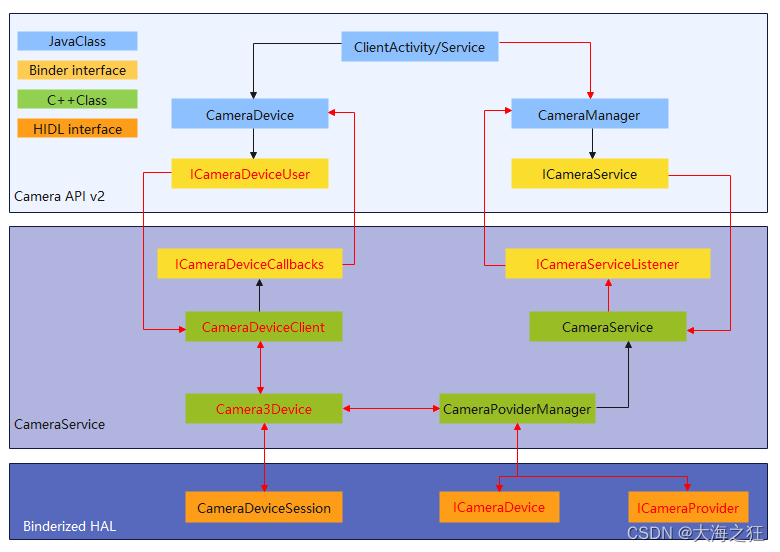
Android相机-架构
引言: 主要是针对CameraAPI v2 HAL3的架构对Android相机系统进行梳理。 相机架构 App和FrameWork Camera API v2位于: packages/apps/Camer2 frameworks/ex/camera2 应用框架级别,使用Camera2 API与相机的硬件进行交互。通过调用Binder接口…...
从C语言到C++_33(C++11_上)initializer_list+右值引用+完美转发+移动构造/赋值
目录 1. 列表初始化initializer_list 2. 前面提到的一些知识点 2.1 小语法 2.2 STL中的一些变化 3. 右值和右值引用 3.1 右值和右值引用概念 3.2 右值引用类型的左值属性 3.3 左值引用与右值引用比较 3.4 右值引用的使用场景 3.4.1 左值引用的功能和短板 3.4.2 移动…...

如何在Linux系统中处理PDF文件?
如何在Linux系统中处理PDF文件? 1.查看PDF文档2.合并PDF文档3.压缩PDF文档4.提取PDF文本 PDF文件是一种特殊的文件格式,它可以在不同的操作系统中实现跨平台的文件传输和共享。Linux系统作为一种自由开放的操作系统,拥有丰富的PDF文件处理工具…...
SpringBoot实现热部署/加载
在我们修改完项目代码后希望不用重启服务器就能把项目代码部署到服务器中(也就是说修改完项目代码后不用重启服务器修改后的项目代码就能生效)。 一、实现devtools原理 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
