LeetCode42.接雨水

这道题呢可以按列来累加,就是先算第1列的水的高度然后再加上第2列水的高度……一直加到最后就是能加的水的高度,我想到了这里然后就想第i列的水其实就是第i-1列和i+1列中最小的高度减去第i列的高度,但是其实并不是,比如示例中的第5列,他的告诉是0左右两边是1,但水是2,然后看题解了。
第i列的水其实与第i-1列和i+1列的水并没有关系,而是和第i列左边所有柱子中最高的和第i列右边所有柱子中最高的有关
当第i列左右两边的最高柱子中较矮的比第i列要高,那么第i列能装的水就是较矮的高度-第i列的高度。如果左右两边最高的柱子都比第i列的柱子矮的话,那么第i列能装的水就是0。所以算出每一列能装的水然后全部加起来就是能接到的雨水,以下的代码:
class Solution {public int trap(int[] height) {int n = height.length;int ans = 0;for(int i =1;i<n-1;i++){int leftMaxHeight =0;for(int j =i-1;j>=0;j--){if(height[j] > leftMaxHeight)leftMaxHeight=height[j];}int rightMaxHeight =0;for(int k =i+1;k<n;k++){if(height[k] > rightMaxHeight)rightMaxHeight=height[k];}int min = Math.min(rightMaxHeight, leftMaxHeight);ans+= min > height[i] ? min-height[i] : 0;}return ans;}
}这个算法每次都要找出某一列左边的最高的柱子和右边的最高柱子,就多了一层循环,算法还可以优化,创建一个left_max数组和right_max数组,left_max[i]表示第i列左边的最高的柱子,right_max[i]同理。用动态规划的方法来填充这两个数组。
left_max[i] = Math,max(left_max[i-1] ,height[i-1]);就是说第i列左边最高的柱子是第i-1列左边的最高柱子第i-1列的高度的最大值,right_max[i]同理。以下是代码:
public int trap(int[] height) {int sum = 0;int[] max_left = new int[height.length];int[] max_right = new int[height.length];for (int i = 1; i < height.length - 1; i++) {max_left[i] = Math.max(max_left[i - 1], height[i - 1]);}for (int i = height.length - 2; i >= 0; i--) {max_right[i] = Math.max(max_right[i + 1], height[i + 1]);}for (int i = 1; i < height.length - 1; i++) {int min = Math.min(max_left[i], max_right[i]);if (min > height[i]) {sum = sum + (min - height[i]);}}return sum;
}
相关文章:

LeetCode42.接雨水
这道题呢可以按列来累加,就是先算第1列的水的高度然后再加上第2列水的高度……一直加到最后就是能加的水的高度,我想到了这里然后就想第i列的水其实就是第i-1列和i1列中最小的高度减去第i列的高度,但是其实并不是,比如示例中的第5…...
优化时间流:区间调度问题的探索与解决
在浩如烟海的信息时代,时间的有效管理成为了一门不可或缺的艺术。无论是生活中的琐事,还是工作中的任务,时间都在无声地流逝,挑战着我们的智慧。正如时间在日常生活中具有的宝贵价值一样,在计算机科学领域,…...
【Python】强化学习:原理与Python实战
搞懂大模型的智能基因,RLHF系统设计关键问答 RLHF(Reinforcement Learning with Human Feedback,人类反馈强化学习)虽是热门概念,并非包治百病的万用仙丹。本问答探讨RLHF的适用范围、优缺点和可能遇到的问题ÿ…...

设计模式——合成复用原则
文章目录 合成复用原则设计原则核心思想合成案例聚合案例继承案例优缺点 合成复用原则 原则是尽量使用合成/聚合的方式,而不是使用继承 设计原则核心思想 找出应用中可能需要变化之处,把它们独立出来,不要和那些不需要变化的代码混在一起。…...

基于OpenCV实战(基础知识一)
目录 简介 1.计算机眼中的图像 2.图片的读取、显示与保存 3.视频的读取与显示 简介 OpenCV是一个流行的开源计算机视觉库,由英特尔公司发起发展。它提供了超过2500个优化算法和许多工具包,可用于灰度、彩色、深度、基于特征和运动跟踪等的图像处理和…...

如何高效的接入第三方接口
作为程序员的我们,经常会接到领导的安排,接入某某的接口,方面我们如何如何, 例如:领导在1号时给作为员工的你说,最近系统需要增加一个新的支付方式,一会和对方技术组建一个群,有什么问题,可以直接在群里说,最近还说,尽快接入,客户等着用,让你在5号前,完成接入工…...

docker pip下载依赖超时或失败问题解决
Docker容器使用pip安装Python库时超时,可能是由于多种原因。以下是一些建议和解决方法: 使用国内镜像源: 如果你位于中国,可以尝试更换到国内的镜像源。例如,可以使用阿里云、腾讯云、清华大学提供的镜像。 你可以在Dockerfile中添…...

python并发编程
一、程序提速的方法 二、python对并发编程的支持 多线程:threading,利用CPU和IO可以同时执行的原理,让CPU不会干巴巴等待IO完成;多进程:multiprocess,利用多核CPU的能力,真正的并行执行任务&am…...

【面试题】:前端怎么实现权限设计及遇到的bug
一.权限的概念 前端权限分为页面权限、按钮权限、API权限。 二.页面权限的实现过程 ①用户登录进去调用获取用户信息接口,后端会给我们返回一个权限标识符 ②在获取到数据之后,我们就要判断用户能访问到哪些页面,我们可以在vuex中permission模块中的action…...

Vue 2 插槽
可以先阅读组件基础-简单了解通过插槽分发内容。 一、插槽定义 插槽将子组件标签间的内容分发到子组件模板的<slot>标签位置。 如果没有<slot>标签,那么该内容将被丢弃。 二、编译作用域 内容在哪个作用域编译,就可以访问哪个作用域的数据…...

Spring 容器启动耗时统计
为了了解 Spring 为什么会启动那么久,于是看了看怎么统计一下加载 Bean 的耗时。 极简版 几行代码搞定。 import org.springframework.beans.BeansException; import org.springframework.beans.factory.config.BeanPostProcessor;import java.util.HashMap; imp…...

1. 优化算法学习
参考文献 1609:An overview of gradient descent optimization algorithms 从 SGD 到 Adam —— 深度学习优化算法概览(一) - 知乎 机器学习札记 - 知乎...

再获荣誉丨通付盾WAAP解决方案获“金鼎奖”优秀金融科技解决方案
今年四月,2023中国国际金融展在首钢会展中心成功落下帷幕。中国国际金融展作为金融开放创新成果的展示、交流、传播平台,历经多年发展,已成为展示中国金融发展成就、宣传金融改革成果、促进金融产业创新和推动金融信息化发展的有效平台。 “金鼎奖”评选…...

【腾讯云 TDSQL-C Serverless 产品测评】“橡皮筋“一样的数据库『MySQL高压篇』
【腾讯云 TDSQL-C Serverless 产品测评】"橡皮筋"一样的数据库 活动介绍服务一览何为TDSQL ?Serverless 似曾相识? 降本增效,不再口号?动手环节 --- "压力"山大实验前瞻稍作简介资源扩缩范围(CCU&…...

python http文件上传
server端代码 import os import cgi from http.server import SimpleHTTPRequestHandler, HTTPServer# 服务器地址和端口 host = 0.0.0.0 port = 8080# 处理文件上传的请求 class FileUploadHandler(SimpleHTTPRequestHandler):def do_POST(self):# 解析多部分表单数据form = …...

Android学习之路(9) Intent
Intent 是一个消息传递对象,您可以用来从其他应用组件请求操作。尽管 Intent 可以通过多种方式促进组件之间的通信,但其基本用例主要包括以下三个: 启动 Activity Activity 表示应用中的一个屏幕。通过将 Intent 传递给 startActivity()&…...
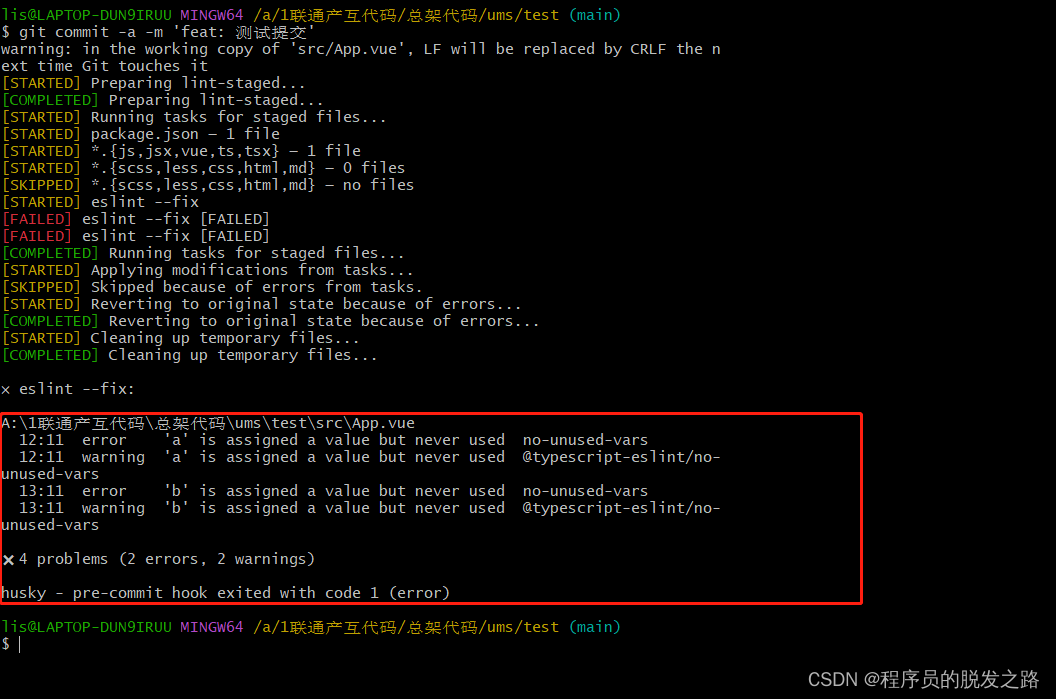
vue项目配置git提交规范
vue项目配置git提交规范 一、背景介绍二、husky、lint-staged、commitlint/cli1.husky2.lint-staged3.commitlint/cli 三、具体使用1.安装依赖2.运行初始化脚本3.在package.json中配置lint-staged4.根目录新增 commitlint.config.js 4.提交测试1.提示信息格式错误时2.eslint校验…...

影响交叉导轨运行速度的因素有哪些?
交叉导轨具有精度高,速度快,承载能力大、结构简单等特点,被广泛应用在固晶机、点胶设备、自动化设备、OA机器及其周边机器、测定器、印刷基板开孔机,精密机器,光学测试仪、光学工作台、操纵机构、X 射缐装置等的滑座部…...

List转Map
一、list转map Map<Long, User> maps userList.stream().collect(Collectors.toMap(User::getId,Function.identity())); 看来还是使用JDK 1.8方便一些。 二、另外,转换成map的时候,可能出现key一样的情况,如果不指定一个覆盖规则&…...

ES:一次分片设计问题导致的故障
### 现象: 1. 单节点CPU持续高 2.写入骤降 3.线程池队列积压,但没有reject 4.使用方没有记录日志 ### 排查 1.ES监控 只能看到相应的结果指标,无法反应出原因。 2.ES日志:大量日志打印相关异常(routate等调用栈&a…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
