当前位置： 首页 > news >正文

计算机网络-物理层(三)-信道的极限容量

news 2026/2/8 9:41:54

计算机网络-物理层(三)-信道的极限容量

当信号在信道中传输失真不严重时，在信道的输出端，这些信号可以被识别

在这里插入图片描述

当信号在信道中，传输失真严重时，在信道的输出端就难以识别

在这里插入图片描述

造成失真的因素

  • 码元传输速率
  • 信号传输距离
  • 噪声干扰
  • 传输媒体质量

奈氏准则

在这里插入图片描述

香农公式

在这里插入图片描述

结论

  • 在信道带宽一定的情况下，根据奈氏准则和香农公式，要想提高信息的传输速率就必须采用多元制（更好的调制方法）和努力提高信道中的信噪比

  • 自从香农公式发表后，各种新的信号处理和调制方法就不断出现，其目的都是为了尽可能的接近香农公式给出得传输速率极限

考研真题

【2014年 题35】下列因素中，不会影响信道数据传输速率的是

  • 信噪比
  • 频率带宽
  • 调制速度
  • 信号传播速度

【2009年 题34】在无噪声情况下，若某通信链路带宽为3kHz，采用4个相位，每个相位具有四种振幅的QAM调制技术，则该通信链路的最大数据传输速率是

  • 12kbps
  • 24kbps
  • 48kbps
  • 96kbps

解析

  • 根据奈氏准则可知，该通信链路的最高码元传输速率= 2 * 3k = 6k (Baud) =6k（码元/秒）
  • 采用4个相位，每个相位4中振幅的QAM调频技术，可以调制出4*4=16个不同的基本波形(码元)，采用二进制对这16个不同的码元进行编码，需要使用4个比特(log2 16=4)。换句话说，每个码元可以携带的信息量为4比特

综上可知，该通信链路的最大数据传输速率=6k（码元/秒）* 4 （比特/码元）=24k（比特/秒）= 24kbps

【2011年 题34】若某通信链路的数据传输速率为2400bps，采用4相位调制，则该链路的波特率是

  • 600波特
  • 1200波特
  • 4800波特
  • 9600波特

解析

  • 采用4相位调制，可以调制出4种相位不同的基本波形(码元)。采用二进制对这4个不同的码元进行编码，需要使用2个比特(log2 4=2)。换句话说，每个码元可以携带的信息量为2个比特

  • 数据传输速率 = 波特率(码元传输速率) * 每个码元所携带的信息量

    2400(比特/秒)=波特率*2(比特/码元)

    解得:波特率=1200（码元/秒）=1200（Baud）=1200波特

【2016年题34】若连接R2和R3链路的频率带宽为8kHz，信噪比为30dB,则该链路实际数据传输速率约为理论最大数据传输速率的50%,则该链路的实际数据传输速率约为

  • 8kbps
  • 20kbps
  • 40kbps
  • 80kbps

解析

理论最大数据传输速率 c= 8k * log2( 1 + S/N)

30(dB) =10 * log10(S/N)(dB) 解得S/N=1000

则该链路的实际数据传输速率 c * 50% = 40 kbps

【2017年 题34】若信道在无噪声情况下的极限数据传输速率不小于信噪比为30dB条件下的极限数据传输速率，则信号状态数至少是

  • 4
  • 8
  • 16
  • 32

解析

设信号状态数(可调制出的不同的基本波形或码元数量)为X

则每个码元可携带的比特数量为log2 X

信道在无噪声情况下的极限数据传输速率（用奈氏准则计算）= 2W （码元/秒）= 2Wlog2 X(比特/秒)

30dB信噪比条件下的极限数据传速率(用香农公式计算)=W log2 (1+1000)（比特/秒）

根据题意列出不等式:2W log2 X ≥ W log2 (1+1000) 解得 X≥32

相关文章：

计算机网络-物理层(三)-信道的极限容量

计算机网络-物理层(三)-信道的极限容量 当信号在信道中传输失真不严重时，在信道的输出端，这些信号可以被识别 当信号在信道中，传输失真严重时，在信道的输出端就难以识别 造成失真的因素 码元传输速率信号传输距离噪声干扰传输媒…...

编程日记 2023/8/24 21:52:37

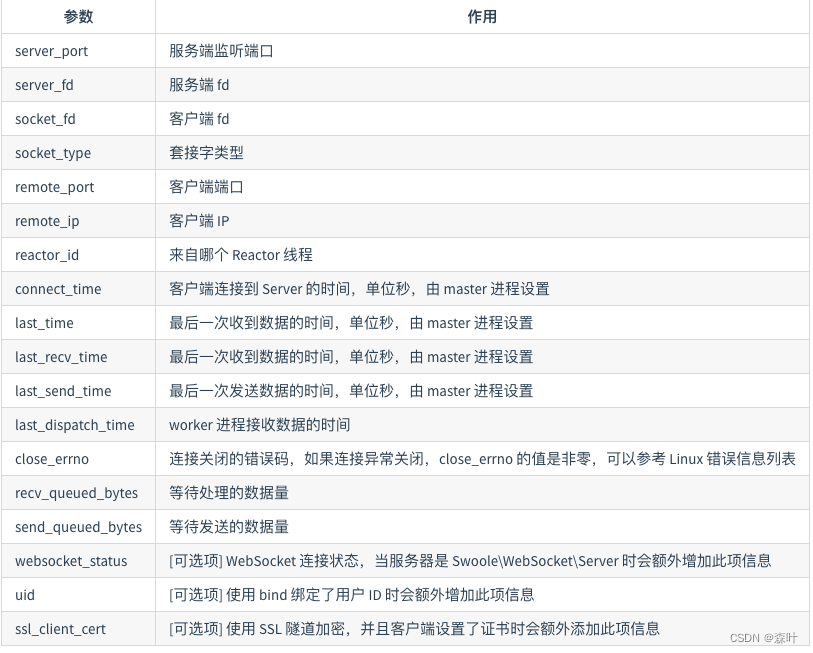
Http/Websocket协议的长连接和短连接的错误认识详细解读（史上最通俗）

从一个问题聊起： Http/Websocket 都称为一种协议，能用现实中的例子来解释协议吗？ AI 举例： 您（客户端）： 您坐在餐厅桌子上，想点一份菜单。 服务员（服务器&#xff09…...

编程日记 2023/8/24 21:51:34

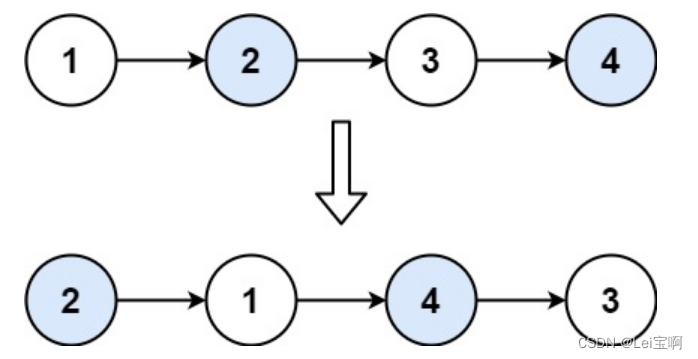
两两交换链表中的节点

你存在，我深深的脑海里~ 题目： 示例： 思路： 这个题有点类似于反转一个单链表，不同的地方在于这个题不全反转，所以我们不同的地方在于此题多用了一个prve指针保存n1的前一个节点，以及头的改变&a…...

编程日记 2023/8/24 21:50:32

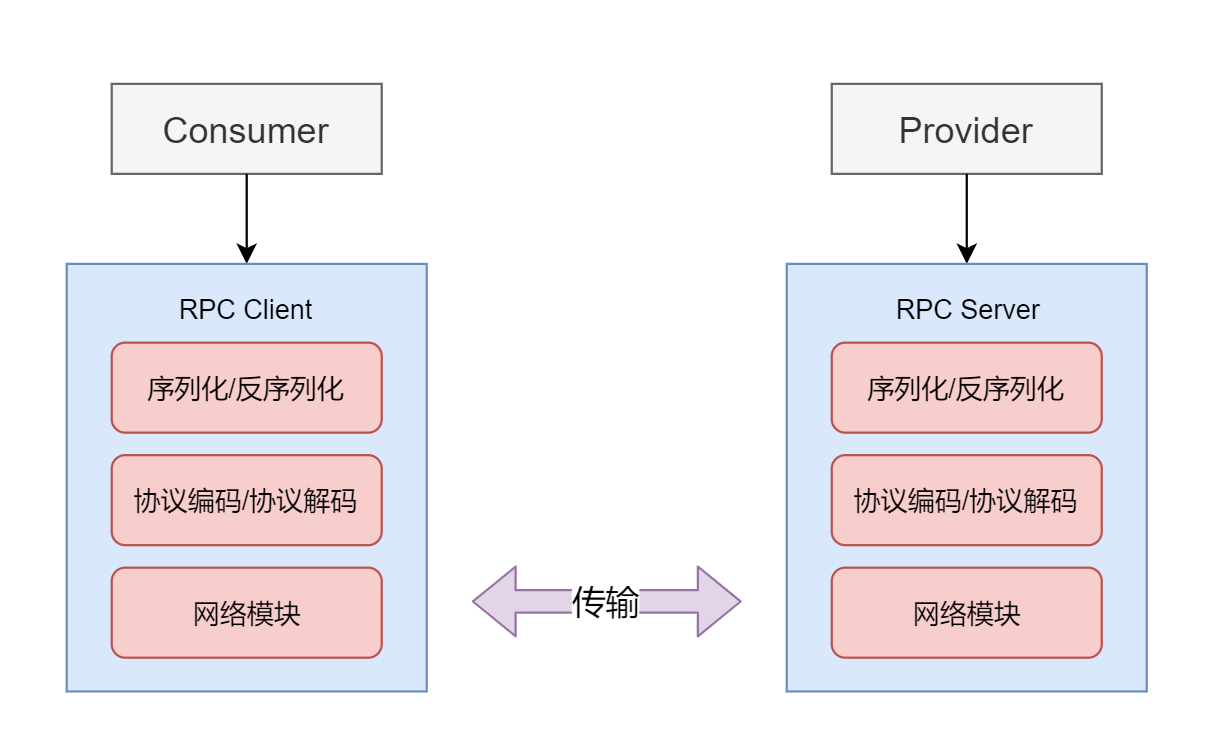
HTTP与RPC的取舍

HTTP与RPC的取舍 HTTP和RPC都是常用的网络通信协议，它们各有优劣。选择何种协议，主要取决于应用的需求和场景。 HTTP和RPC都有各自的优点和缺点，首先我们对两种协议进行一个总结。 HTTP协议图 HTTP的优点： 广泛的支持&#xff1…...

编程日记 2023/8/24 21:49:31

微前端学习（上）

一、课程目标 微前端概念；现有方案利弊；Single-spa实现原理；掌握使用qiankun搭建微应用；二、课程大纲 微前端背景现在web应用面临的问题微前端的价值微前端应用具备哪些能力微前端解决方案有哪些基于qiankun的实践1、微前端背景 2014年: Martin Fowler和James Lewis共同提…...

编程日记 2023/8/24 21:48:30

【Axure视频教程】标签版多选下拉列表

今天教大家在Axure里如何制作标签版多选下拉列表的原型模板，该模板用中继器制作，制作完成后使用也方便，只需要在中继器表格里维护选项信息，即可自动生成交互效果，包括显示隐藏选项列表，选中和取消选中选项&…...

编程日记 2023/8/24 21:47:28

Sharepoint2013必备软件安装路径

SP2013是最后一个有foundation版本的，后续各个版本都是server版，要买lisence。免费的可以用，但安装组件有些链接已经失效了，自己手动下载的路径备份一下，已经下载好的完整版，在文章最后可以直接下载&#x…...

编程日记 2023/8/24 21:46:26

C++day4（关系运算符的重载）

关系运算符重载的作用&#xff1a;可以让两个自定义类型对象进行对比操作。 代码实现关系运算符的重载&#xff1a; #include <iostream>using namespace std;class Person {// friend const Person operator(const Person &L, const Person &R); private:int …...

编程日记 2023/8/24 21:45:25

农业水价综合改革系统主要组成

一、系统概述 农业水价改革灌区信息化系统主要由感知采集层、网络传输层、系统应用层等部分组成。通过无线技术、感知层技术与新型应用的有效结合&#xff0c;可以用于各种业务的传送&#xff0c;充分满足灌区监测站间的物与物互联&#xff0c;农业生产的自动化和信息化相结合。…...

编程日记 2023/8/24 21:44:24

使用批处理文件(.bat)启动多个CMD窗口并执行命令

由于每次启动本机的mongodb和kafka&#xff0c;都需要进入相关目录进行启动&#xff0c;操作相对繁琐&#xff0c;于是想起了批处理来帮忙一键启动。 在桌面新建一个txt文件&#xff0c;改后缀名为.bat&#xff0c;并加上下面的代码。 cd /d D:\env-java\mongodb-win32-x86_64…...

编程日记 2023/8/24 21:43:23

开源项目-会议室预约管理系统

哈喽，大家好，今天给大家带来一个开源项目-会议室管理系统。项目基于SpringBoot+VUE开发。 会议室管理系统主要分为 前台会议室预约管理系统 和 会议室后台管理系统 两部分 前台会议室预约管理系统主要有申请会议室，预约进程，查看历史会议三部分 后台管理系统主要有会议室…...

编程日记 2023/8/24 21:42:21

Flask路由注册route的几种方式

前言 Flask路由注册的三种方式&#xff1a; app.routeapp.add_url_rule蓝图 app.route&#xff08;添加变量&#xff09; from flask import Flaskapp Flask(__name__) app.config.from_pyfile(config/base_setting.py) app.route("/") def hello():return "…...

编程日记 2023/8/24 21:41:21

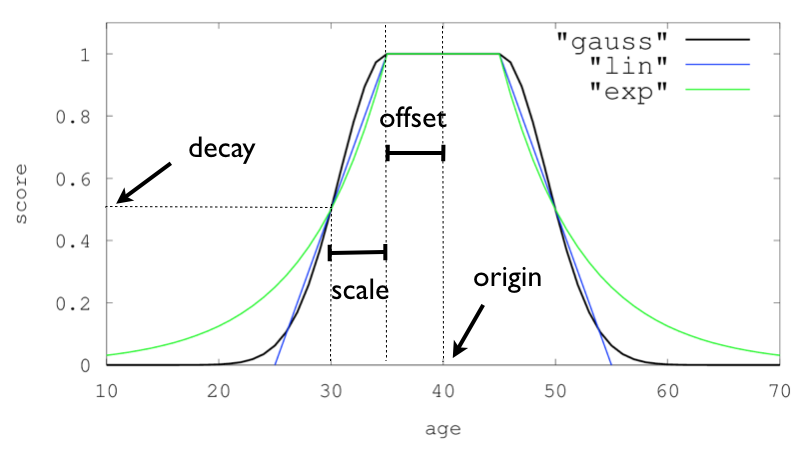
Elasticsearch 查询之Function Score Query

前言 ES 的主查询评分模式分为两种&#xff0c;是信息检索领域的重要算法&#xff1a; TF-IDF 算法 和 BM25 算法。 Elasticsearch 从版本 5.0 开始引入了 BM25 算法作为默认的文档评分&#xff08;relevance scoring&#xff09;算法。在此之前&#xff0c;Elasticsearch 使…...

编程日记 2023/8/24 21:40:19

【3D激光SLAM】LOAM源代码解析--scanRegistration.cpp

系列文章目录 【3D激光SLAM】LOAM源代码解析–scanRegistration.cpp 【3D激光SLAM】LOAM源代码解析–laserOdometry.cpp 【3D激光SLAM】LOAM源代码解析–laserMapping.cpp 【3D激光SLAM】LOAM源代码解析–transformMaintenance.cpp 写在前面 本系列文章将对LOAM源代码进行讲解…...

编程日记 2023/8/24 21:39:18

解锁ChatGLM-6B的潜力：优化大语言模型训练，突破任务困难与答案解析难题

解锁ChatGLM-6B的潜力&#xff1a;优化大语言模型训练&#xff0c;突破任务困难与答案解析难题 LLM&#xff08;Large Language Model&#xff09;通常拥有大量的先验知识&#xff0c;使得其在许多自然语言处理任务上都有着不错的性能。 但&#xff0c;想要直接利用 LLM 完成…...

编程日记 2023/8/24 21:38:16

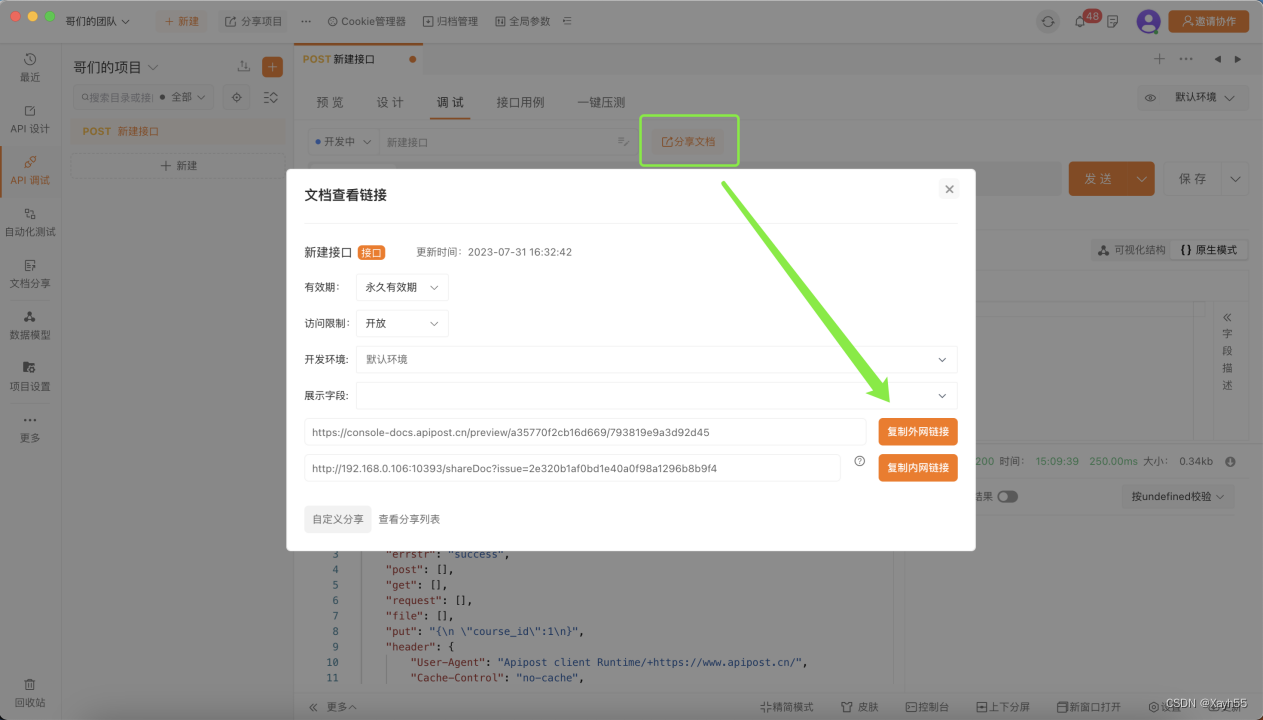
Apipost：提升API开发效率的利器

在数字化时代&#xff0c;API已经成为企业和开发者实现业务互通的关键工具。然而&#xff0c;API的开发、调试、文档编写以及测试等工作繁琐且复杂。Apipost为这一问题提供了完美的解决方案。 Apipost是一款专为API开发人员设计的协同研发平台&#xff0c;旨在简化API的生命周…...

编程日记 2023/8/24 21:37:15

论文解读：Image-Adaptive YOLO for Object Detection in Adverse Weather Conditions

发布时间&#xff1a;2022.4.4 (2021发布&#xff0c;进过多次修订) 论文地址&#xff1a;https://arxiv.org/pdf/2112.08088.pdf 项目地址&#xff1a;https://github.com/wenyyu/Image-Adaptive-YOLO 虽然基于深度学习的目标检测方法在传统数据集上取得了很好的结果&#xf…...

编程日记 2023/8/24 21:36:13

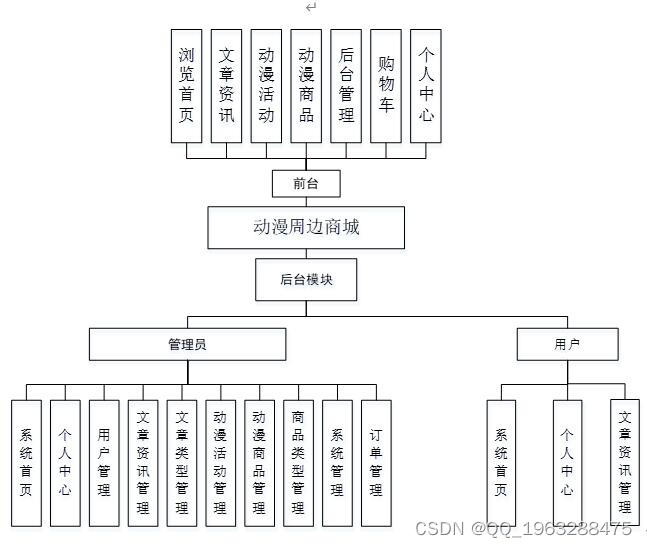
springboot 基于JAVA的动漫周边商城的设计与实现64n21

动漫周边商城分为二个模块&#xff0c;分别是管理员功能模块和用户功能模块。管理员功能模块包括&#xff1a;文章资讯、文章类型、动漫活动、动漫商品功能&#xff0c;用户功能模块包括&#xff1a;文章资讯、动漫活动、动漫商品、购物车&#xff0c;传统的管理方式对时间、地…...

编程日记 2023/8/24 21:35:12

uniapp - 全平台兼容实现上传图片带进度条功能，用户上传图像到服务器时显示上传进度条效果功能（一键复制源码，开箱即用）

效果图 uniapp小程序/h5网页/app实现上传图片并监听上传进度，显示进度条完整功能示例代码 一键复制，改下样式即可。 全部代码 记得改下样式，或直接...

编程日记 2023/8/24 21:34:11

第 7 章 排序算法(2)(冒泡排序)

7.5冒泡排序 7.5.1基本介绍 冒泡排序&#xff08;Bubble Sorting&#xff09;的基本思想是&#xff1a;通过对待排序序列从前向后&#xff08;从下标较小的元素开始&#xff09;,依次比较相邻元素的值&#xff0c;若发现逆序则交换&#xff0c;使值较大的元素逐渐从前移向后部…...

编程日记 2023/8/24 21:33:09

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密

在实际项目中，用户注册、登录、修改密码等操作，都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输，在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

编程新知 2025/11/28 6:00:25

Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务

通过akshare库&#xff0c;获取股票数据&#xff0c;并生成TabPFN这个模型 可以识别、处理的格式&#xff0c;写一个完整的预处理示例&#xff0c;并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务&#xff0c;进行预测并输…...

编程新知 2025/9/20 4:34:47

如何在看板中有效管理突发紧急任务

在看板中有效管理突发紧急任务需要&#xff1a;设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP&#xff08;Work-in-Progress&#xff09;弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中&#xff0c;设立专门的紧急任务通道尤为重要&#xff0c;这能…...

编程新知 2026/2/3 22:50:06

GitHub 趋势日报 (2025年06月08日)

&#x1f4ca; 由 TrendForge 系统生成 | &#x1f310; https://trendforge.devlive.org/ &#x1f310; 本日报中的项目描述已自动翻译为中文 &#x1f4c8; 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

编程新知 2025/12/13 1:32:15

微信小程序云开发平台MySQL的连接方式

注&#xff1a;微信小程序云开发平台指的是腾讯云开发 先给结论&#xff1a;微信小程序云开发平台的MySQL&#xff0c;无法通过获取数据库连接信息的方式进行连接&#xff0c;连接只能通过云开发的SDK连接&#xff0c;具体要参考官方文档&#xff1a; 为什么&#xff1f; 因为…...

编程新知 2026/2/1 5:24:17

人机融合智能 | “人智交互”跨学科新领域

本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

编程新知 2026/1/25 13:33:35

【MATLAB代码】基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），附源代码|订阅专栏后可直接查看

文章所述的代码实现了基于最大相关熵准则（MCC）的三维鲁棒卡尔曼滤波算法（MCC-KF），针对传感器观测数据中存在的脉冲型异常噪声问题，通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现，验证了后者在状态估计鲁棒性方面的显著优…...

编程新知 2026/1/28 9:00:05

wpf在image控件上快速显示内存图像

wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像&#xff08;比如分辨率3000*3000的图像&#xff09;的办法&#xff0c;尤其是想把内存中的裸数据&#xff08;只有图像的数据&#xff0c;不包…...

编程新知 2026/1/31 9:25:11

【LeetCode】算法详解#6 ---除自身以外数组的乘积

1.题目介绍 给定一个整数数组 nums&#xff0c;返回 数组 answer &#xff0c;其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&#xff0c;且在 O…...

编程新知 2026/2/1 20:47:10

k8s从入门到放弃之HPA控制器

k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率&#xff08;或其他自定义指标&#xff09;来调整这些对象的规模&#xff0c;从而帮助应用程序在负…...

编程新知 2025/10/30 1:59:28