【秋招基础】后端开发——笔面试常见题目
综述:
💞目的:本系列是个人整理为了秋招算法的,整理期间苛求每个知识点,平衡理解简易度与深入程度。
🥰来源:材料主要源于网上知识点进行的,每个代码参考热门博客和GPT3.5,其中也可能含有一些的个人思考。
🤭结语:如果有帮到你的地方,就点个赞和关注一下呗,谢谢🎈🎄🌷!!!
🌈【C++】秋招&实习面经汇总篇
文章目录
- 编码平台格式
- ACM模式
- 输入部分
- 算法部分
- 输出部分
- 笔试基础
- 面试基础
- 面试常见手撕题目
- 基本操作
- 项目基础
- 设计模式
- 高并发相关
- 场景题目
- 智力题
- 待解决问题
😊点此到文末惊喜↩︎
编码平台格式
ACM模式
输入部分
- 注意事项
使用long代替int:标准规定int 至少 16 位,long int 至少 32 位,并且 sizeof(int) <= sizeof(long),所以在不同的编译器下,int可能位数不足出现整形溢出问题。- 奇数判断
(n & 1) == 1:因为奇数的二进制尾数为1,二进制速度快。
- 基础输入要点
- 引用库需要自己加上对应的库,如
#include <algorithm> - 输入使用
while (cin >> a ){ 算法主体 } - 输出使用
cout,注意删除自己的测试输出,不能使用return,否则会一直报错语法错误 - 输入示例:
#include <vector> #include <iostream> using namespqce std; int main() {long n = 0; // 表示n轮输入cin >> n;while (n--) { int c = 0; // 每轮输入的整数个数cin >> c;vector<long> vec(c, 0);for (int i = 0; i < vec.size(); ++i)cin >> vec[i]; } - 引用库需要自己加上对应的库,如
- 二维数组的初始化
vector<vector<int>> dp(rows, vector<int>(cols, 0));// 注意要进行初始化 for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {cin >> dp[i][j];// 不能使用push_back()进行处理 } - 输入一行以回车结尾的数字
vector<int> vec; int tmp = 0; do {// 不能使用while(){},因为会丢失第一个输入cin >> tmp;vec.push_back(tmp); } while (cin.get() != '\n');
算法部分
输入部分进行健壮性检查:尽量将代码进行划分,然后对每个部分进行健壮性检查。含有小数的计算要注意使用double
输出部分
- 输出要使用
endl进行换行cout << val << endl; - 价格通常要输出小数后两位数
- 注意使用
double,如果空间不足再使用float
double val = 2.34535; printf("%.2f\n", val); - 注意使用
笔试基础
基本代码范式
- 基本逻辑范式
bool function(){// 1.健壮性检查if (函数形参不符合情况) {doing();return false;}// 2.初始化:给工作变量赋初值,符合要求的第一次循环条件int initial_value = 0;// 会被算法初始化的也应该赋初值// 4.算法逻辑while (工作变量符合算法循环条件) {// 注意考虑最后不足算法增量的部分doing();// 对结果序列操作的函数工作变量的迭代;// 注意工作变量在使用完成后已经被污染}// 5.收尾处理不足最后一次算法增量的部分return true; } - 递归逻辑范式
void Recursion(vector<int> &vec,...){// 递归出口if (结束条件) return ;// 递归体Doing(); }
基本算法框架
- 快慢指针
- 作用:可用于线性结构的条件遍历处理,如链表、数组等
- 优点:可以将
两次循环降维成条件筛选+一次循环
// 示例:删除数组中的元素 int RemoveElement(vector<int>& nums, int val) {// 健壮性检查if (nums.empty()) return -1;// 初始化操作int slow = 0; // 慢指针负责更新处理int fast = slow; // 快指针负责拓展选择// 算法部分while(fast < nums.size()){ if(nums[fast] != val){ // 快指针负责条件判断nums[slow] = nums[fast];++slow;++fast;}++fast;}return slow; } // 示例:环形链表的入口 - 滑动窗口
- 右边界指针负责拓展,左边界指针负责收缩
void SlideWindow(vector<int> vec) {// 功能函数部分auto slide_windows = [](vector<int> &nums, int left, int right){// 直到到大窗口的右边界// 直到到达窗口右边界停止while(right < nums.size()) {// - 扩大右边界并更新窗口状态...right++;// - 窗口到达什么状态需要收缩while(需要收缩) {// - 缩小左边界并更新窗口状态...left++;}}};// 代码逻辑部分// 健壮性处理if (nums.size() <= 1) return ;// 初始化int left = 0;int right = 0;// 算法部分slide_windows(vec, left, right); } - 二叉树遍历算法
- 广度优先遍历
- 深度优先遍历
// 二叉树的基本数据结构 struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int v) : val(v), left(nullptr), right(nullptr){} }; // 深度优先的递归遍历 // 中序遍历 void Traversal(TreeNode *root) {if (root == nullptr) return ;Traversal(root->left); // 左Doing(root->val); // 中Traversal(root->right); // 右 } // 深度优先的非递归遍历 vector<int> Traversal(TreeNode* root) {// 初始化vector<int> result; // 结果容器stack<TreeNode*> st; // 深度的栈if (root != NULL) // 根非空则入栈st.push(root);// 遍历源容器while (!st.empty()) {TreeNode* node = st.top(); // if (node != NULL) {st.pop();// 算法变化的部分,遍历的逆序// 中st.push(node); st.push(NULL);// 右if (node->right) st.push(node->right); // 左if (node->left) st.push(node->left); } else {// 对值节点的处理st.pop();// 弹出空值结点node = st.top();st.pop();// 结点处理result.emplace_back(node->val);}}return result; } // 广度优先的非递归遍历 vector<vector<int>> Traversal(TreeNode* root) {// 初始化vector<vector<int>> result; // 结果容器queue<TreeNode*> que; // 广度的队列if(root != nullptr) // 根非空则入列 que.push(root);// 算法while (!que.empty()) { // 队列非空vector<int> vec; // 结果存放TreeNode* node; // 过程记录int size = que.size(); // 初始化:记录每层要遍历的根节点数量for (int i = 0; i < size; i++) { // que.size()会变化// 处理结点node = que.front(); // 记录队首结点que.pop(); // 弹出队首结点if (node->left) que.push(node->left); // 不需要node->left != nullptrif (node->right) que.push(node->right);// doing:处理结点vec.emplace_back(node->val);}// 将每层筛选元素压入结果数组中result.emplace_back(vec);}// 输出return result; } - 回溯算法
- 组合问题
- 有重复元素的组合
- 无重复元素的组合
- 排列问题
- 有重复元素的全排列
- 无重复元素的全排列
- 组合问题
// 组合问题
// 无重复元素的组合
class Solution {
public:vector<vector<int>> combine(vector<int>vec, int k) {result.clear(); // 可以不写path.clear(); // 可以不写BackTracking(vec, 0, k);return result;}
private:// 回溯核心算法vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void Backtracking(vector<int> &vec, int start, int target) {// 递归出口:满足条件则加入结果集中if (path.size() == target) {result.push_back(path); return ;}// 回溯算法for (int i = start; i < vec.size(); ++i) {// 剪枝条件if (i > vec.size() - (target-path.size())) continue;path.push_back(vec[i]); // 做出选择Backtracking(vec, i + 1, target);// 递归path.pop_back(); // 撤销选择}}
};// 有重复元素的组合
class Solution {
public:vector<vector<int>> combine(vector<int> vec, int k) {result.clear(); // 可以不写path.clear(); // 可以不写sort(vec.begin(), vec.end());BackTracking(vec, 0, k);return result;}
};
private:// 回溯核心算法vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void BackTracking(vector<int> &vec, int start, int target) {// 递归出口:满足条件则加入结果集中if (path.size() == target) {result.push_back(path); return ;}// 回溯算法for (int i = start; i < vec.size(); i++) {// 剪枝:重复选择只选一次,需要配合sort使用if (i > start && vec[i] == vec[i - 1]) continue;// 回溯步骤path.push_back(vec[i]); // 做出选择BackTracking(vec, i + 1, target);// 递归path.pop_back(); // 撤销选择}}
};// 无重复元素的全排列
class Solution {
public:vector<vector<int>> permute(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);backtracking(nums, used);return result;}
private:vector<vector<int>> result;vector<int> path;void backtracking (vector<int>& nums, vector<bool>& used) {// 此时说明找到了一组if (path.size() == nums.size()) {result.push_back(path);return;}for (int i = 0; i < nums.size(); i++) {if (used[i] == true) continue; // path里已经收录的元素,直接跳过// 增加选择used[i] = true;path.push_back(nums[i]);// 回溯backtracking(nums, used);// 撤销选择path.pop_back();used[i] = false;}}
};// 有重复元素的全排列
class Solution {
public:vector<vector<int>> permuteUnique(vector<int>& nums) {// 重复计数unordered_map<int, int> umap;for (auto i : nums) ++umap[i];backtrace(umap, 0, nums.size());return res;}
private:vector<vector<int> > res;vector<int> path;void backtrace(unordered_map<int, int> &umap, int k, int total) {if (k == total) {res.push_back(path);return;}for (auto& p : umap) { // 每轮递归结束会进入循环if (p.second == 0) continue;--p.second;path.push_back(p.first);backtrace(umap, k + 1, n);++p.second;path.pop_back();}}
};- 动态规划算法
// dp的推导 // - dp[j]为容量为j的背包所背的最大价值 // - 每次物品有两个选择 // - 放入则背包减去重量并增加价值 dp[j - weight[i]] + value[i] // - 不放入则仍为 dp[j] // 最终递推公式为dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); int main() {// 子功能部分auto bag_problem = [](vector<int> &weight, vector<int> &value, int bag_weight)->int{vector<int> dp(bag_weight + 1, 0);for (int i = 0; i < weight.size(); ++i) {// 倒叙保证物品只添加一次,顺序会导致所用数据是刚更新的// 而不是上一层滚动的for (int j = bag_weight; j >= weight[i]; --j) {dp[j] = max(dp[j], dp[j-weight[i]] + value[i]);}}return dp[bag_weight];};// 逻辑部分vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bag_weight = 4;cout << bag_problem(weight, value, bag_weight); }
< a l g o r i t h m > 常用函数模板 <algorithm>常用函数模板 <algorithm>常用函数模板
- 前提:需要包含
#include<algorithm>头文件 - 常见功能函数使用示例
#include <iostream> #include <algorithm> #include <vector> using namespace std; int main() {vector<int> vec{1, 2, 3, 4, 5};// max和min函数int min_val = min(a, b); // 返回a和b中较小的值int max_val = max(a, b); // 返回a和b中较大的值// sort函数:对容器进行自定义的排序sort(vec.begin(), vec.end()); // 默认为升序排序sort(vec.begin(), vec.end(), [](int a, int b){return a < b; // 可以进行自定义}); // 降序排序// find函数:返回容器中指定值的迭代器,如果没有则返回end()auto it = find(vec.begin(), vec.end(), 3);if (it != vec.end()) cout << "找到了";// remove函数:删除范围内的指定值remove(vec.begisn(), vec.end(), 3);// replace函数:将容器中的所有a值替换成b值replace(v.begin(), v.end(), 3, 10); // 将所有3替换成10// reverse函数:反转vector中的元素reverse(vec.begin(), vec.end());// count函数:计算在一个范围内某个值的出现次数int n = count(vec.begin(), vec.end(), 3);// 注意若为字符使用'3'// swap函数:交换两个变量的值swap(a, b);// 使用lower_bound函数查找第一个大于等于3的元素位置auto it = lower_bound(vec.begin(), vec.end(), 3);cout << it - vec.begin() << endl; }
面试基础
面试常见手撕题目
- 快速排序
void QuickSort(vector<int> &vec, int left, int right) {// 功能性函数:划分auto partition = [](vector<int> &vec, int left, int right)->int{ int pivot = vec[left]; // 定义第一个为枢纽while (left < right) {// 从右向前找比枢纽值小的放在左边while (left < right && vec[right] >= pivot) --right;vec[left] = vec[right];// 从左向后找比枢纽值大的放在右边while (left < right && vec[left] <= pivot ) ++left;vec[right] = vec[left];}// 填入枢纽值vec[left] = pivot;return left;};// 递归出口(需要使用大于等于)if (left >= right) return ;// [left, right]中left=right,表示区间有序// 递归体int pivot_index = partition(vec, left, right);QuickSort(vec, left, pivot_index-1);QuickSort(vec, pivot_index+1, right); } - 合并两个有序链表
- 合并k个有序链表:使用合并两个有序链表作为基础进行归并算法
ListNode* MergeList(ListNode* list1, ListNode* list2) {// 健壮性检查if (list1 == nullptr || list2 == nullptr) return (list1 != nullptr) ? list1 : list2;// 初始化TreeNode *vhead = ListNode(-1);TreeNode *cur = vhead;// 算法while (list1 != nullptr && list2 != nullptr) {if (list1.val < list2.val) {cur.next = list1;list1 = list1.next;} else {cur.next = list2;list2 = list2.next;}cur = cur.next;}// 收尾cur.next = (list1 != nullptr) ? list1 : list2;return vhead; } - 求第k大数(含有重复数)
#include <algorithm> #include <vector> #include <algorithm> using namespqce std;int KthLargeElement(vector<int> &vec, int k) {// 健壮性检查if (k <= 0 || k > vec.size())return INT_MIN;// 初始化sort(vec.begin(), vec.end(), [](int a, int b){return a > b;});int count = 1;// 算法部分for (int i = 1; i < vec.size(); ++i) {// key:相邻遍历的方式if (vec[i] != vec[i-1]) ++count;if (count == k) break;}// 收尾return vec[i]; }
基本操作
-
去重
#include <iostream> #include <vector> #include <unordered_set> using namespace std; int main() {// 基本去重vector<int> vec = { 1, 2, 3, 1, 3 };// 使用set去重的天然特性,然后再赋值给原容器unordered_set<int> uset(vec.begin(), vec.end());vec = vector<int>(uset.begin(), uset.end());// keyreturn 0; } -
遍历相邻元素
int sum = 0; for (int i = 1; i < vec.size(); ++i) {sum += vec[i] - vec[i-1]; } -
字符串转换
-
进制转换
-
删除链表next结点
auto delete_node = [](TreeNode *cur){if (cur != nullptr) {ListNode* tmp = cur->next;cur->next = cur->next->next;delete tmp;} }; -
字符串切割
在这里插入代码片
项目基础
设计模式
- 消息队列(生产者消费者模式)
#include <iostream> #include <condition_variable> #include <mutex> #include <queue> #include <string> #include <thread> using namespace std;class MessageQueue {public:MessageQueue() {}// 生产者放入消息队列中void PushMsq(string msg) {unique_lock<mutex> lock(mtx_);// 1.上锁:保证{}范围内的互斥访问que_.push(msg); // 2.生产:向消息队列中添加消息 cv_.notify_one();// 3.唤醒:唤醒在该条件变量上等待队列优先级最高的一个线程// m_cv.notify_all()会唤醒所有线程,但是会造成资源争用,要谨慎使用}// 消费者从消息队列中取出信息string PopMsq() {unique_lock<mutex> lock(mtx_);// 1. 上锁// 2. 队列为空则等待:如果队列为空,等待生产者添加消息while (que_.empty()) {cv_.wait(lock);// 释放lock锁并阻塞等待}// 3. 消费:取出消息并返回string msg = que_.front();que_.pop();return msg;}private:// 记住这个顺序:先加智能锁,然后压入队列,最后唤醒条件变量上的线程mutex mtx_; // 互斥锁:保证消息队列和条件变量的互斥访问queue<string> que_; // 消息队列:生产者和消费者的缓冲区condition_variable cv_; // 条件变量:保证生产者和消费者的同步 }; // 定义生产者线程函数 void producer(MessageQueue& mq) {for (int i = 0; i < 10; ++i) {string msg = "message " + to_string(i);mq.PushMsq(msg);this_thread::sleep_for(chrono::milliseconds(100)); // 生产者线程休眠一段时间} } // 定义消费者线程函数 void consumer(int id, MessageQueue& mq) {for (int i = 0; i < 5; ++i) {string msg = mq.PopMsq();cout << "consumer " << id << " get message: " << msg << std::endl;this_thread::sleep_for(chrono::milliseconds(200)); // 消费者线程休眠一段时间} } // 测试生产者消费者模型 int main() {MessageQueue msq;// 线程的创建:参数为(函数指针,函数形参)thread t1(producer, ref(msq));thread t2(consumer, 1, ref(msq));thread t3(consumer, 2, ref(msq));thread t4(consumer, 3, ref(msq));// .join()执行完当前线程再向下执行t1.join();t2.join();t3.join();t4.join();return 0; } - 线程安全的单例模式
// 饿汉式 class SinglePatter {public:static SinglePatter& GetInstance() {static SinglePatter instance;return instance;}private:SinglePatter(){};SinglePatter(SinglePatter &) = delete;SinglePatter& operator=(const SinglePatter &) = delete; };// 懒汉式 class SinglePatter {public: static SinglePatter *GetInstance() {unique_lock<mutex> lock(mtx);if (instance == nullptr) {instance = new SinglePatter();}return instance;}private:static SinglePatter *instance;static mutex mtx;SinglePatter(){};SinglePatter(SinglePatter &) = delete;SinglePatter& operator=(const SinglePatter &) = delete;};
高并发相关
- 写一个自旋锁
// 自旋锁 int xchg(volatile int *addr, int new_val) {int res;asm volatile( // 将lock xchg换位cmpxhg是否就是CAS锁"lock xchg %0, %1":"+m"(*addr),"=a"(res):"1"(new_val):"cc");return res; }int locked = 0; void lock(){while (xchg(&locked, 1)); } void unlock(){xchg(&locked, 0); }
场景题目
智力题
- 数学归纳法(动态规划核心公式的推导)
- 推导前三个或者五个简单的输入和输出,从而假设递进关系式
- 再使用两个进行验证
- 组合排列问题
待解决问题
-
功能性函数auto封装导致的代码优雅性问题,字节二面上下左右走格子中,使用回溯增加复杂性,但是代码优雅易于理解。
-
匿名函数只是一个对数据的单纯的逻辑处理,不应该有健壮性检查和返回值,数据的初始化部分应该由实参传输,除内部工作变量外,其他变量应该由外部提供。
相关文章:

【秋招基础】后端开发——笔面试常见题目
综述: 💞目的:本系列是个人整理为了秋招算法的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于网上知识点进行的,每个代码参考热门博客和GPT3.5࿰…...
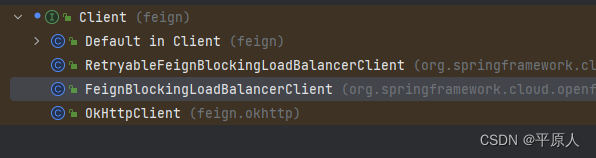
自定义loadbalance实现feignclient的自定义路由
自定义loadbalance实现feignclient的自定义路由 项目背景 服务A有多个同事同时开发,每个同事都在dev或者test环境发布自己的代码,注册到注册中心有好几个(本文nacos为例),这时候调用feign可能会导致请求到不同分支的服务上面,会…...
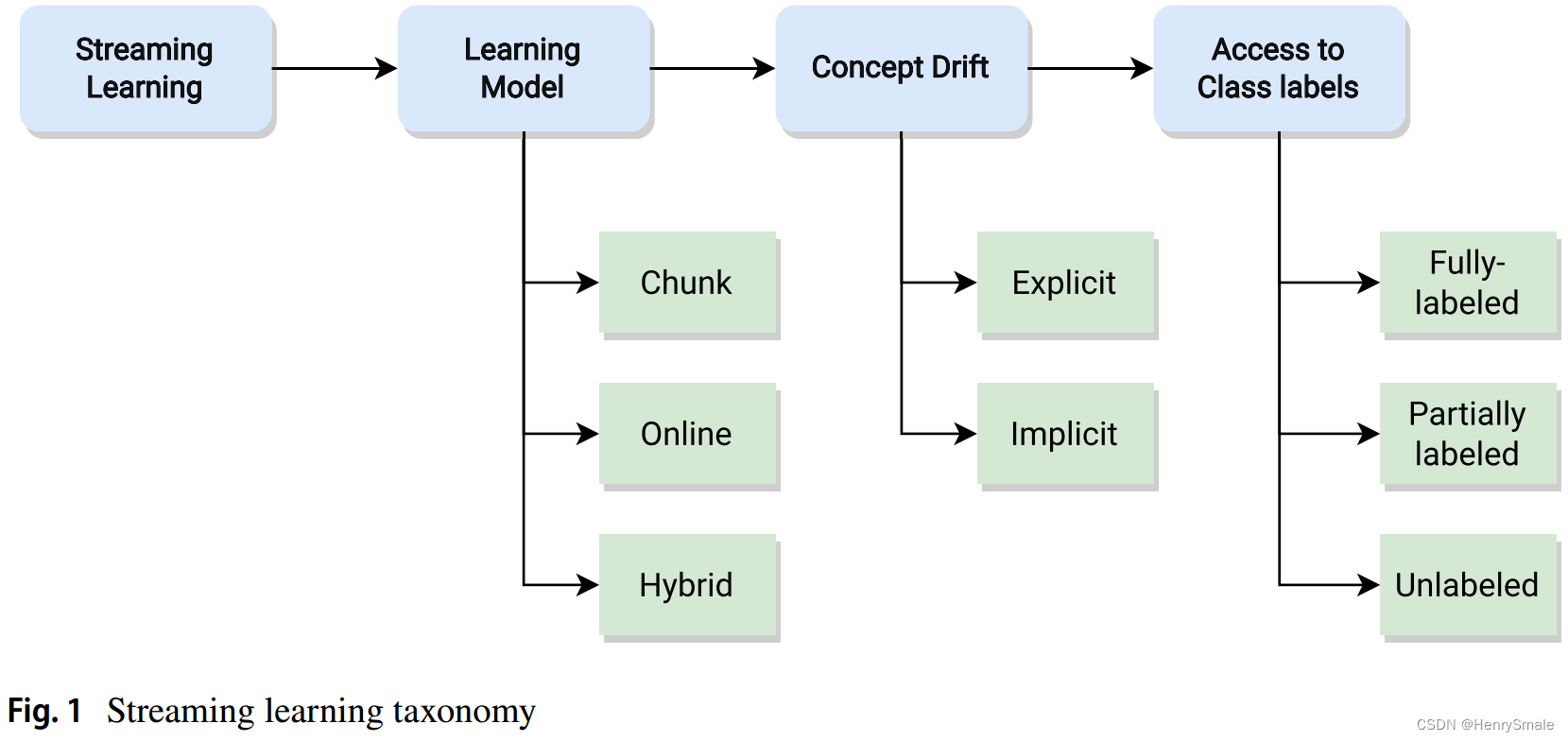
论文笔记:从不平衡数据流中学习的综述: 分类、挑战、实证研究和可重复的实验框架
0 摘要 论文:A survey on learning from imbalanced data streams: taxonomy, challenges, empirical study, and reproducible experimental framework 发表:2023年发表在Machine Learning上。 源代码:https://github.com/canoalberto/imba…...

C#设计模式六大原则之--迪米特法则
设计模式六大原则是单一职责原则、里氏替换原则、依赖倒置原则、接口隔离原则、迪米特法则、开闭原则。它们不是要我们刻板的遵守,而是根据实际需要灵活运用。只要对它们的遵守程度在一个合理的范围内,努为做到一个良好的设计。本文主要介绍一下.NET(C#)…...

一次js请求一般情况下有哪些地方会有缓存处理?
目录 1、DNS缓存 2、CDN缓存 3、浏览器缓存 4、服务器缓存 1、DNS缓存 DNS缓存指DNS返回了正确的IP之后,系统就会将这个结果临时储存起来。并且它会为缓存设定一个失效时间 (例如N小时),在这N小时之内,当你再次访问这个网站时࿰…...
)
CSDN编程题-每日一练(2023-08-24)
CSDN编程题-每日一练(2023-08-24) 一、题目名称:计算公式二、题目名称:蛇形矩阵三、题目名称:小玉家的电费一、题目名称:计算公式 时间限制:1000ms内存限制:256M 题目描述: 给定整数n。 计算公式: n i-1 ∑ ∑ [gcd(i + j, i - j) = 1] i=1 j=1 输入描述: 输入整数n…...

怎么把PDF转成Word?需要注意什么事项?
PDF是一种常见的文档格式,但是与Word文档不同,PDF文件通常不能直接编辑。如果您想编辑PDF文件中的文本,或者想将PDF文件转换为Word文档,下面我们就来看一看把PDF转成Word有哪些方法和注意事项。 PDF转Word工具 有许多将PDF转换为…...

USACO22OPEN Pair Programming G
P8273 [USACO22OPEN] Pair Programming G 题目大意 一个程序由一系列指令组成,每条指令的类型如下: d \times d d,其中 d d d是一个 [ 0 , 9 ] [0,9] [0,9]范围内的整数 s s s,其中 s s s是一个表示变量名称的字符串ÿ…...

实战分享之springboot+easypoi快速业务集成
1.依赖引入 <!--引入EasyPOI--><dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-base</artifactId><version>4.1.0</version></dependency><dependency><groupId>cn.afterturn</group…...
)
金字塔原理(思考的逻辑)
前言:前面学习了表达的逻辑,那在表达之前,如何组织内容?如何进行思考?接下来看第二篇——思考的逻辑。 目录 应用逻辑顺序 时间顺序 结构顺序 程度顺序 概括各组思想 什么是概括? 思想表达方式 如…...
和反向传播(Back propagation))
机器学习之前向传播(Forward Propagation)和反向传播(Back propagation)
前向传播(Forward Propagation)和反向传播(Back propagation)是深度学习中神经网络训练的两个关键步骤。 前向传播(Forward Propagation): 定义:前向传播是指从神经网络的输入层到输…...
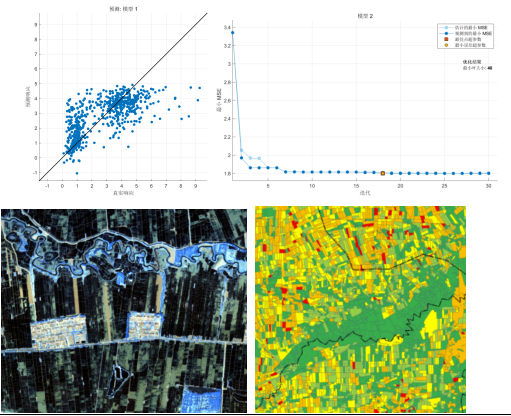
Matlab高光谱遥感数据处理与混合像元分解实践技术
光谱和图像是人们观察世界的两种方式,高光谱遥感通过“图谱合一”的技术创新将两者结合起来,大大提高了人们对客观世界的认知能力,本来在宽波段遥感中不可探测的物质,在高光谱遥感中能被探测。以高光谱遥感为核心,构建…...

Docker consul的容器服务注册与发现
前言一、服务注册与发现二、consul 介绍三、consul 部署3.1 consul服务器3.1.1 建立 Consul 服务3.1.2 查看集群信息3.1.3 通过 http api 获取集群信息 3.2 registrator服务器3.2.1 安装 Gliderlabs/Registrator3.2.2 测试服务发现功能是否正常3.2.3 验证 http 和 nginx 服务是…...

Spring注入外部 工厂类Bean
问题 对于一些使用建造者模式的 Bean,我们往往不能直接 new 出来,这些 Bean 如果需要注册到 Spring 容器中,我们就需要使用工厂类。 比如我们项目中经常使用的okhttp: 如果我们想把OkHttpClient注册到Spring容器中,该怎么做? …...

WPF网格拖动自动布局效果
WPF网格拖动自动布局效果 使用Canvas和鼠标相关事件实现如下的效果: XAML代码: <Window x:Class="CanvasTest.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:...
排名)
肯德尔秩相关系数(Kendall‘s Tau)排名
肯德尔秩相关系数(Kendall’s Tau)是一种用于衡量两个排列之间相似性的统计指标,它考虑了元素之间的顺序关系而不考虑具体数值。该系数被广泛用于排序、排名和比较不同实验结果的相关性等领域。 具体而言,肯德尔秩相关系数衡量了…...

电脑怎么把视频转换gif动图?视频生成gif的操作步骤
如果你也想把一些精彩的视频转gif图片(https://www.gif.cn)的话,今天的文章你可千万不要错过,利用专业的视频转gif工具,轻松在线视频转gif,操作简单又方便,支持电脑、手机双端操作,赶…...
使用 docker 搭建 granfana+prometheus 监控平台监控测试服务器资源
互联网发展的今天,人们对互联网产品的用户体验要求也越来越高,企业为了能提供更优质的用户体验,就会绞尽脑汁想尽各种办法。而对于服务器的资源监控,搭建一个资源监控平台,就是一个很好的维护优质服务的保障平台。利用…...
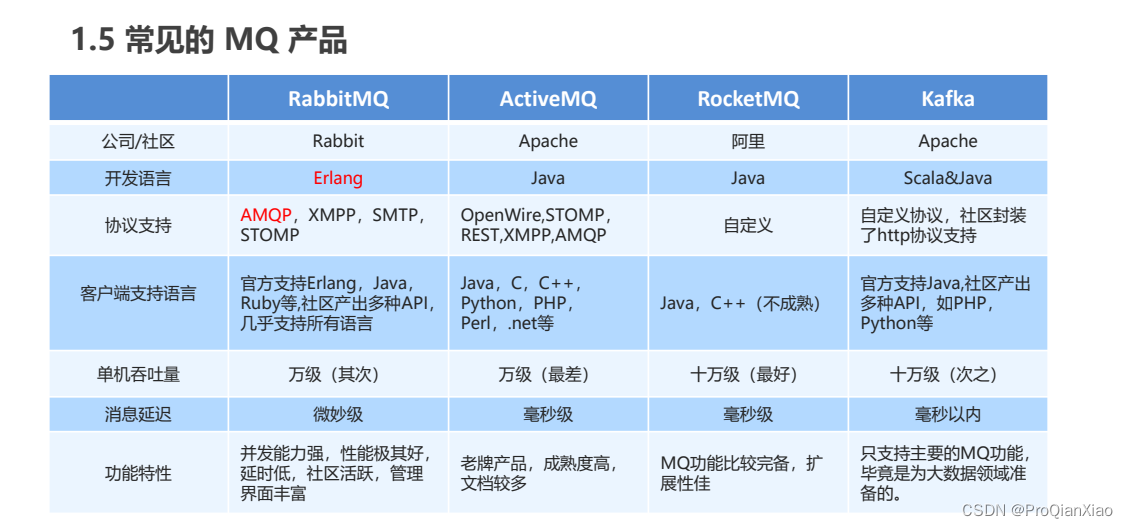
一、MQ的基本概念
1、初识MQ MQ全称是Message Queue,消息队列,多用于系统之间进行异步通信。队列的概念数据结构中有详细介绍过,先进先出,消息队列就是存储消息的数据结构。 同步调用和异步调用两者之间的区别: 同步调用:发…...

Android面试题:MVC、MVP、MVVM
MVC模式: MVC结构: 1.MVC(Model-View-Controller) 2.Model:对数据库的操作、对网络等的操作都应该在Model里面处理,当然对业务计算,变更等操作也是必须放在的该层的。 3.View:主要包括一下View及ViewGroup控件,可以是…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
