远控木马病毒分析
一、病毒简介
SHA256:880a402919ba4e896f6b4b2595ecb7c06c987b025af73494342584aaa84544a1
MD5:0902b9ff0eae8584921f70d12ae7b391
SHA1:f71b9183e035e7f0039961b0ac750010808ebb01

二、行为分析
同样在我们win7虚拟机中,使用火绒剑进行监控,分析行为特征:

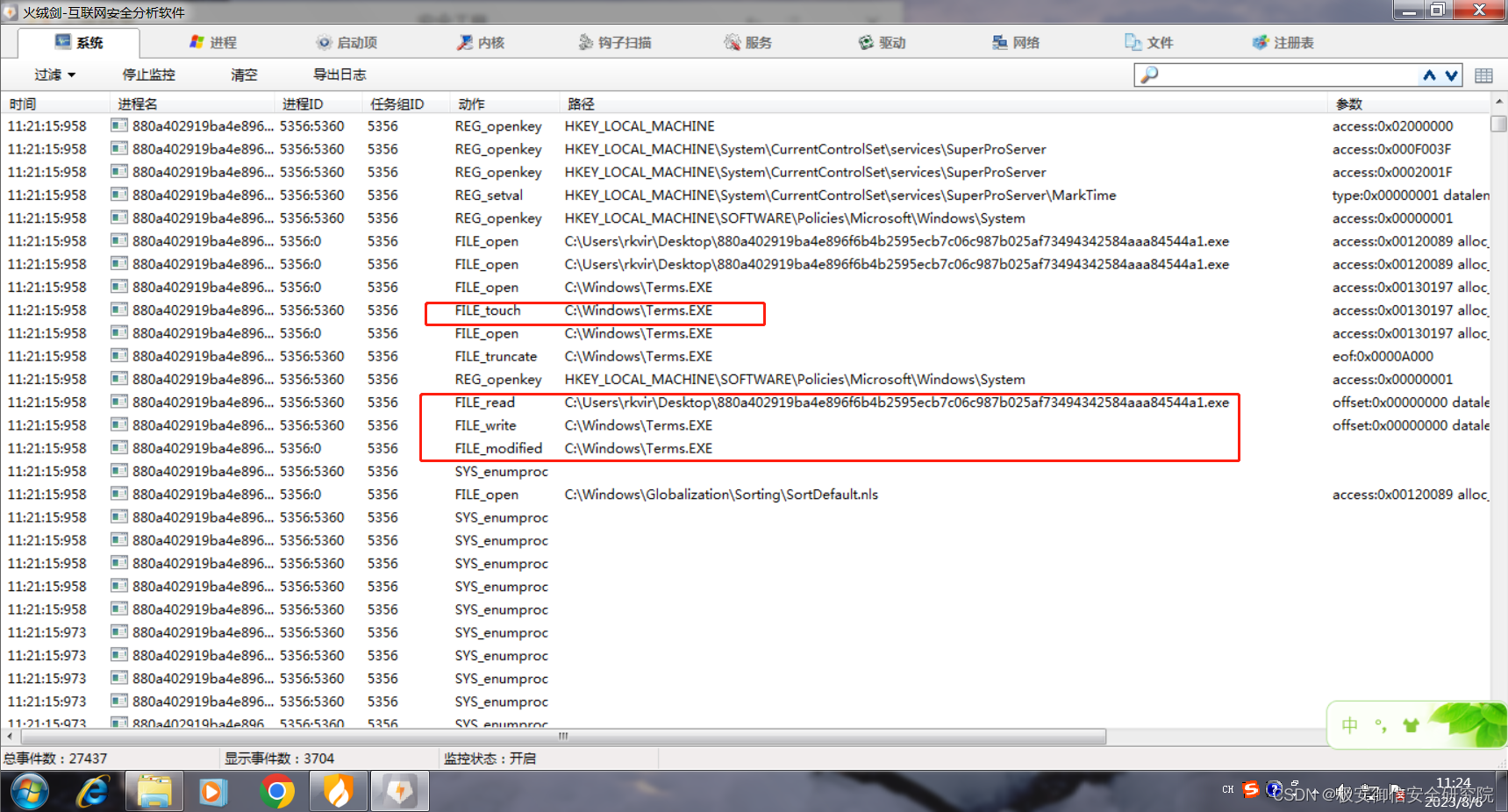

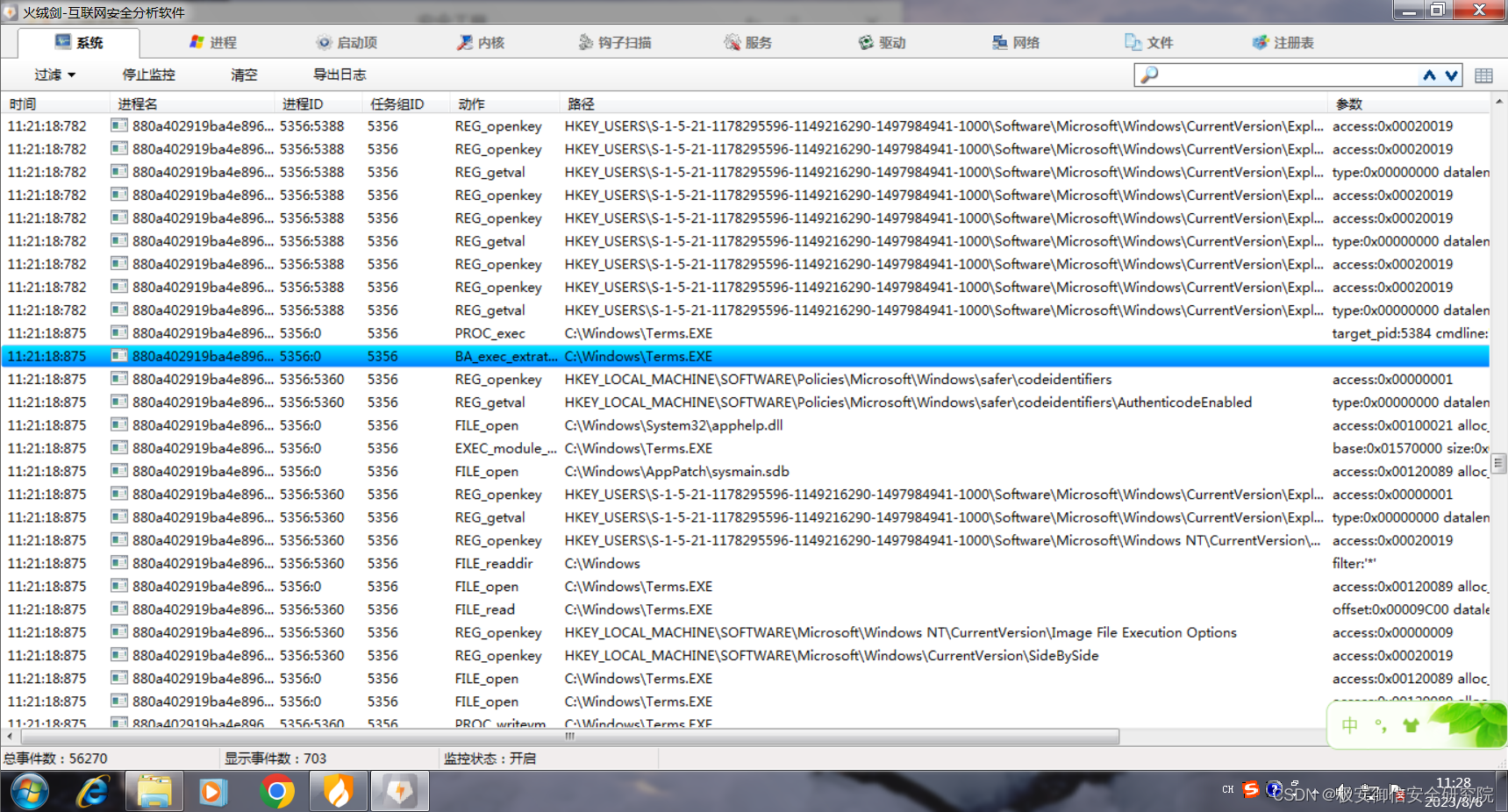
首先是一个拷贝自身,而在后面也被行为检测标蓝;

其次就是大量的枚举进程;
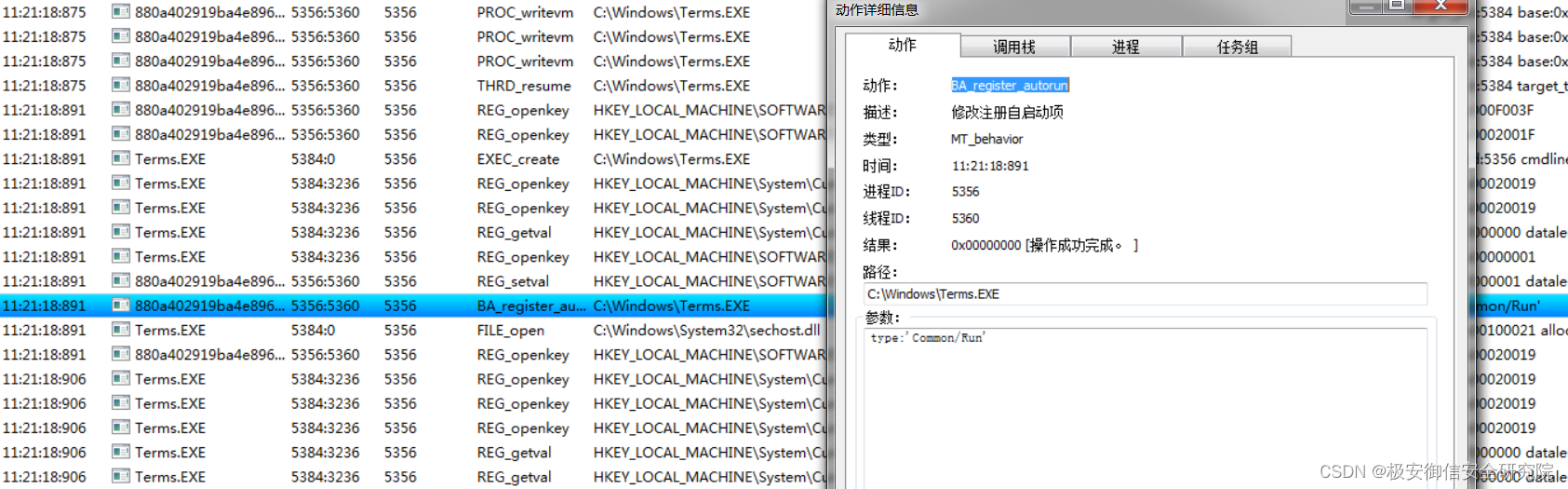

这里启动了释放的文件,并设置了自启动;
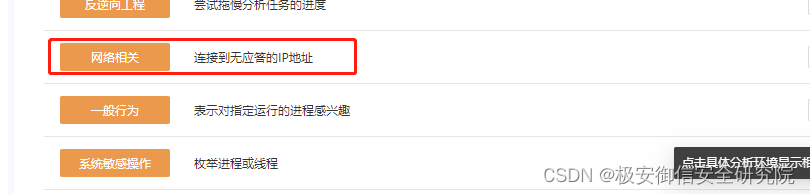

结合这里,获取信息没有和服务端取得联系,IP已经失效,所以在火绒剑中也没有检测到网络链接。
三、逆向分析
拖进DIE查查壳,显示无壳:


看看导入表信息:


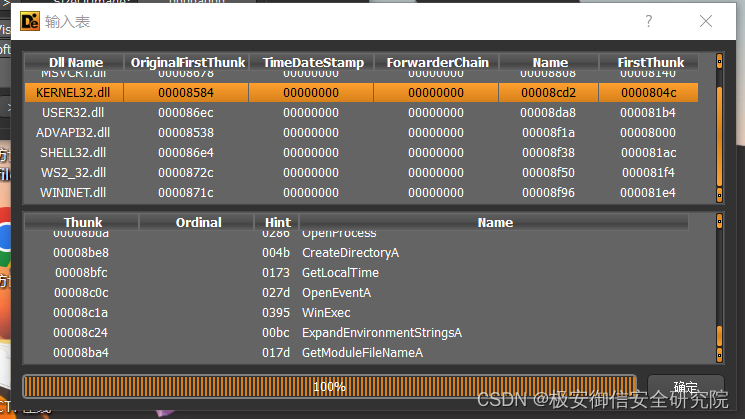
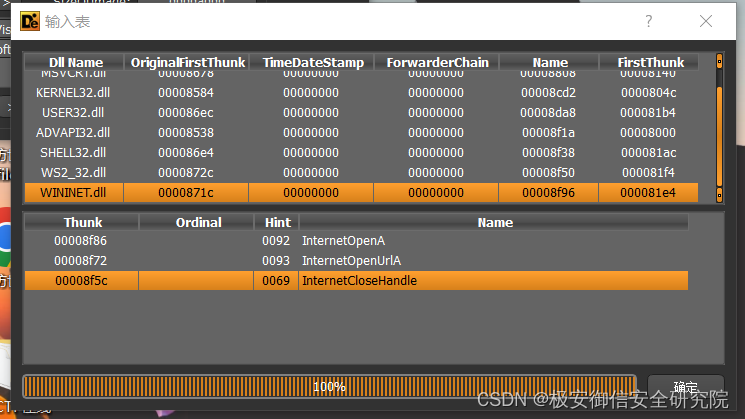
这里有检索主机信息之类的函数,还有网络链接之类的函数,基本可以确定大致行为,结合这里,在IDA中静态分析,进入winmain,F5看伪代码:




 以上就是main函数主体,接下来对关键函数进行详细分析:
以上就是main函数主体,接下来对关键函数进行详细分析:
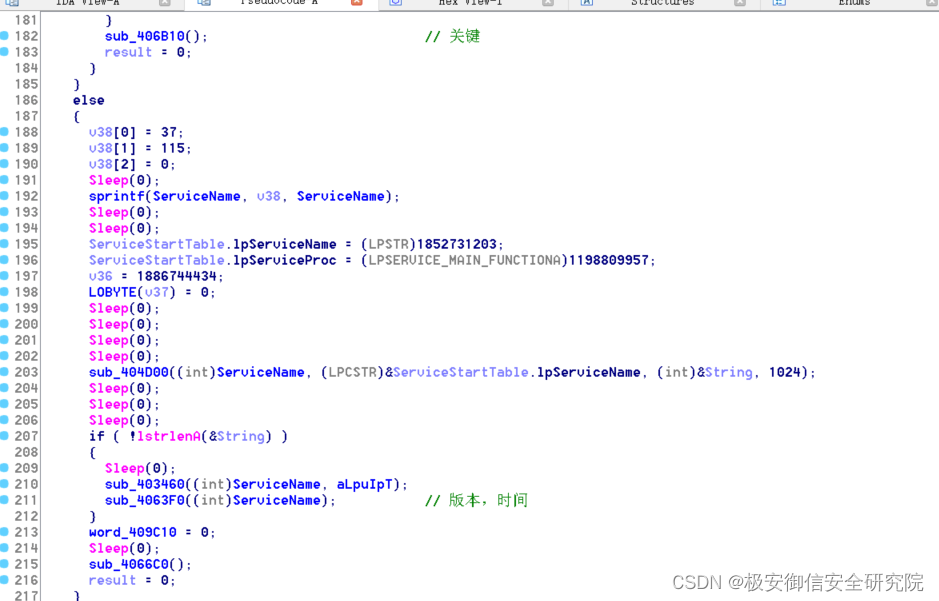

3.1、sub-406A30
进入函数内部,是俩个函数:




根据特征,很明显这里是rc4的解密,当然我是动态调试直接看他解密结果,解密一个服务名,一个IP地址,SuperProServer和127.0.0.1;
3.2、sub-4056C0
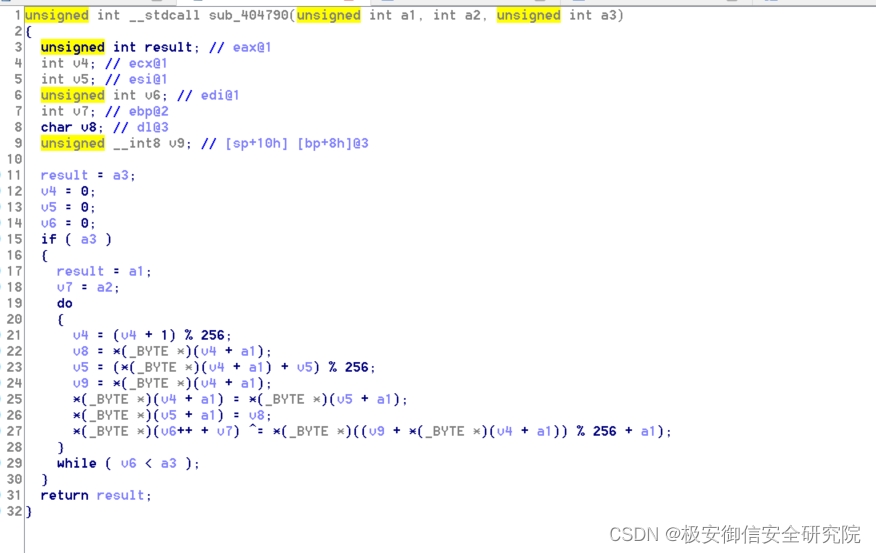

这里获取当前进程路径;


这里生成随机数并进行拼接,生成一个路径,创建一个文件并写入内容;


这里进行shell启动进程,可见这里是一个拷贝自身并启动的操作;
3.3、sub-406B50
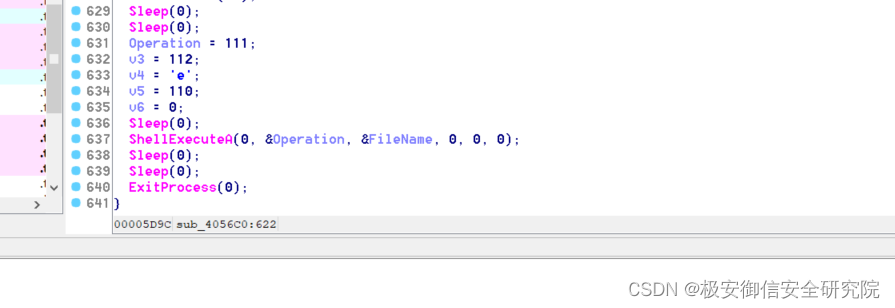

进入此函数,内部有函数sub_407660,根据传参是rundll32.exe,进入此函数:


可以看到这里是进程遍历,返回进程信息,回到上一层:


这里是启动命令行杀掉rundll32.exe,返回主函数;
3.4、sub_4070E0


进入函数内部:




可以看到这里是设置病毒为服务并设置相关注册表版本类信息;
3.5、sub-407660


这里是循环三次,找病毒本体,通过函数40766寻找,找到后进行启动,进入函数内部:


这里是创建快照找相应进程的操作,而传入的参数就是Terms.exe;
3.6、sub_405480




这里是设置自启动;
3.7、sub_406B10
跟进此函数:
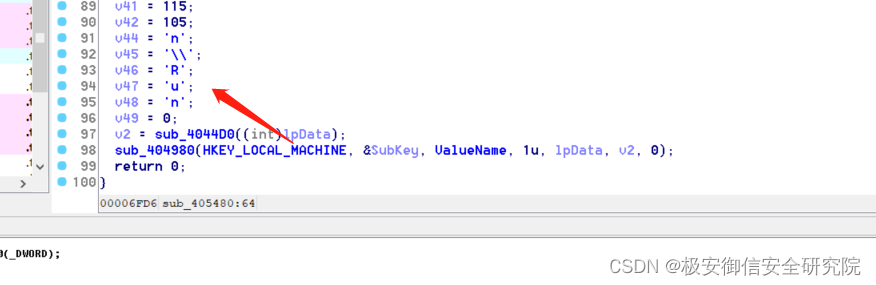

3.7.1、sub_406290


进入406170:
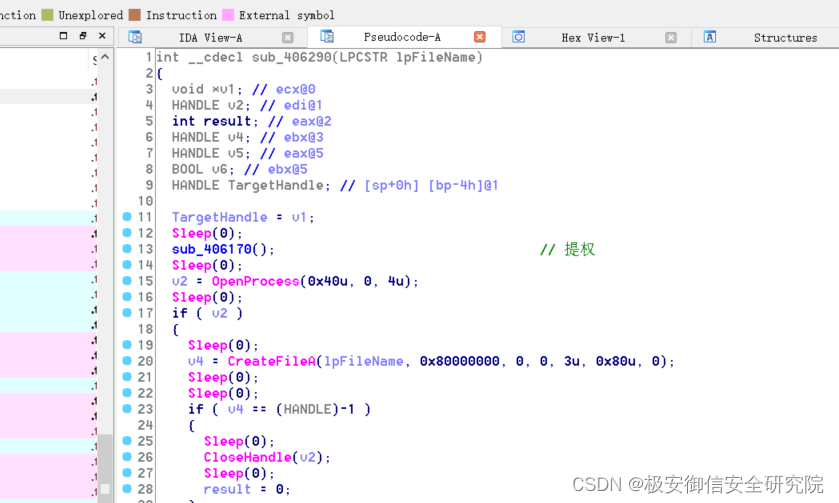

这是一套令牌提权的组合拳,返回上一层;


这里是拿到句柄复制句柄;
3.7.2、sub_4066C0
这边就开始和服务通信sub_401470:


sub_401660:




这里有一个开辟线程,进入回调函数发现,是和服务器链接,接受内容,并通过rc4解密,在自身开辟空间,进行写入操作,后面这块分析比较粗浅,但大体内容就是这些;
相关文章:

远控木马病毒分析
一、病毒简介 SHA256:880a402919ba4e896f6b4b2595ecb7c06c987b025af73494342584aaa84544a1 MD5:0902b9ff0eae8584921f70d12ae7b391 SHA1:f71b9183e035e7f0039961b0ac750010808ebb01 二、行为分析 同样在我们win7虚拟机中,使用火绒剑进行监控,分析行为…...
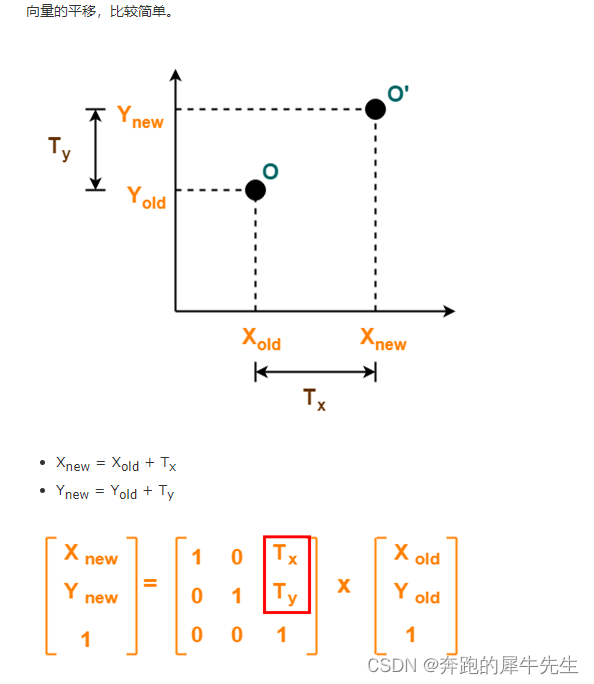
线性代数的学习和整理7:各种特殊效果矩阵汇总
目录 1 矩阵 1.1 1维的矩阵 1.2 2维的矩阵 1.3 没有3维的矩阵---3维的是3阶张量 1.4 下面本文总结的都是各种特殊效果矩阵特例 2 方阵: 正方形矩阵 3 单位矩阵 3.1 单位矩阵的定义 3.2 单位矩阵的特性 3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]…...

[git]github上传大文件
github客户端最高支持100Mb文件上传,如果要>100M只能用git-lfs,但是测试发现即使用git lfs,我上传2.5GB也不行,测试737M文件可以,GitHub 目前 Git LFS的总存储量为1G左右,超过需要付费。(上传失败时&…...

element ui - el-select获取点击项的整个对象item
1.背景 在使用 el-select 的时候,经常会通过 change 事件来获取当前绑定的 value ,即对象中默认的某个 value 值。但在某些特殊情况下,如果想要获取的是点击项的整个对象 item,该怎么做呢? 2.实例 elementUI 中是可…...

实现SSM简易商城项目的购物车实现
实现SSM简易商城项目的购物车实现 在这篇博客中,我们将使用SSM框架来实现一个简易的购物车功能。我们将使用Spring框架来管理Bean,使用SpringMVC框架来处理HTTP请求,使用MyBatis框架来操作数据库。 实现SSM简易商城项目的购物车功能的思路如…...
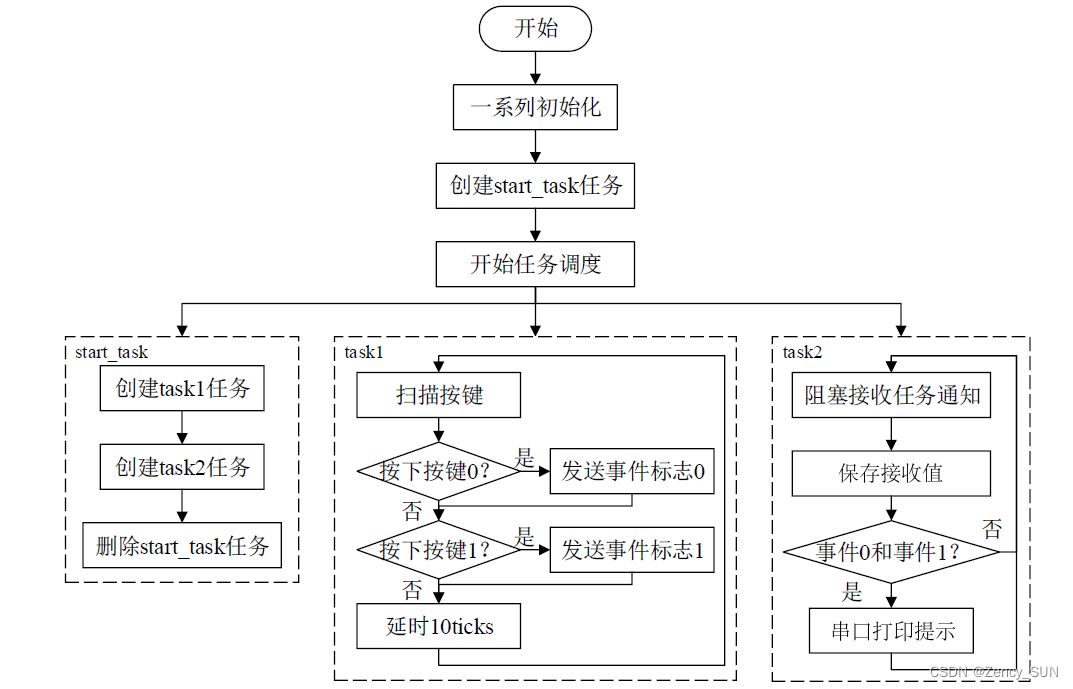
【学习FreeRTOS】第17章——FreeRTOS任务通知
1.任务通知的简介 任务通知:用来通知任务的,任务控制块中的结构体成员变量 ulNotifiedValue就是这个通知值。 使用队列、信号量、事件标志组时都需另外创建一个结构体,通过中间的结构体进行间接通信! 使用任务通知时,…...
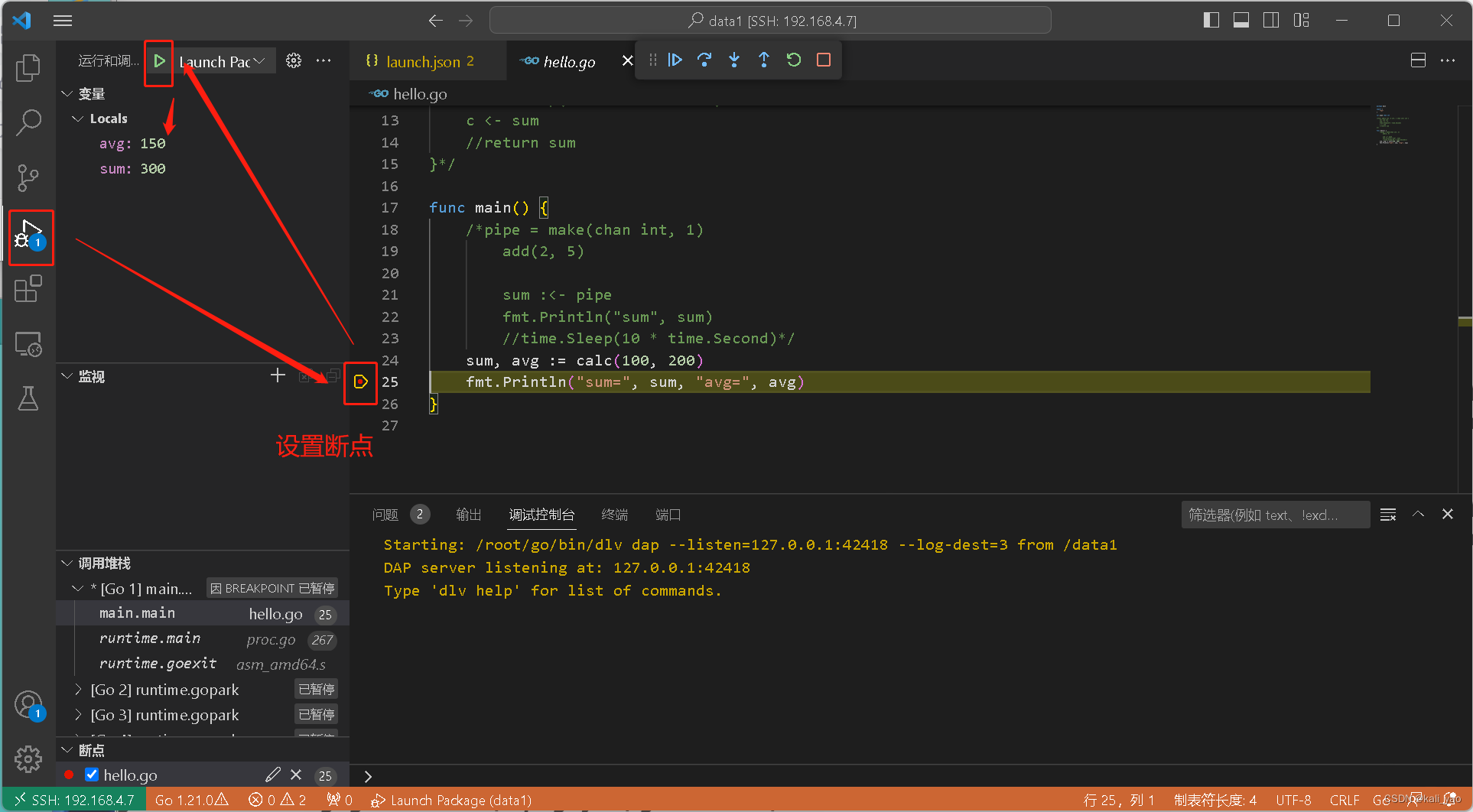
GO-vscode远程开发和调试
本文内容主要包括: 概述: 主要就是把代码放到服务器上然后远程去开发和调试 工具: vscode 远程端: linux 一.安装远程插件 vscode安装Remote - SSH,Remote Explorer,Remote Development,…...

【笔记】判断两个Double类型的值是否相同
在Java中,将两个double值转换为String类型,然后使用equals方法进行比较是一个常见的做法,但是这种方法并不是完全可靠,特别是在涉及浮点数的精度时仍然可能会遇到问题。 浮点数在内部以二进制表示,有时会存在舍入误差…...
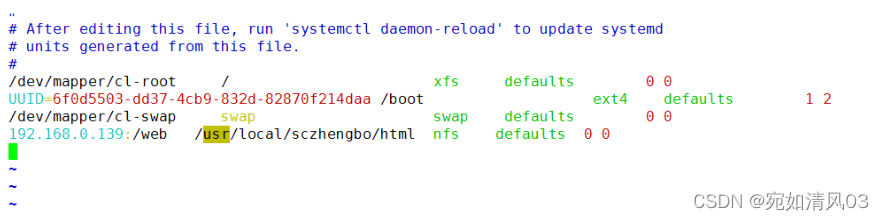
Linux —— nfs文件系统
简介 NFS 是Network File System的缩写,即网络文件系统。一种使用于分散式文件系统的协定,由Sun公司开发,于1984年向外公布。功能是通过网络让不同的机器、不同的操作系统能够彼此分享个别的数据,让应用程序在客户端通过网络访问位…...
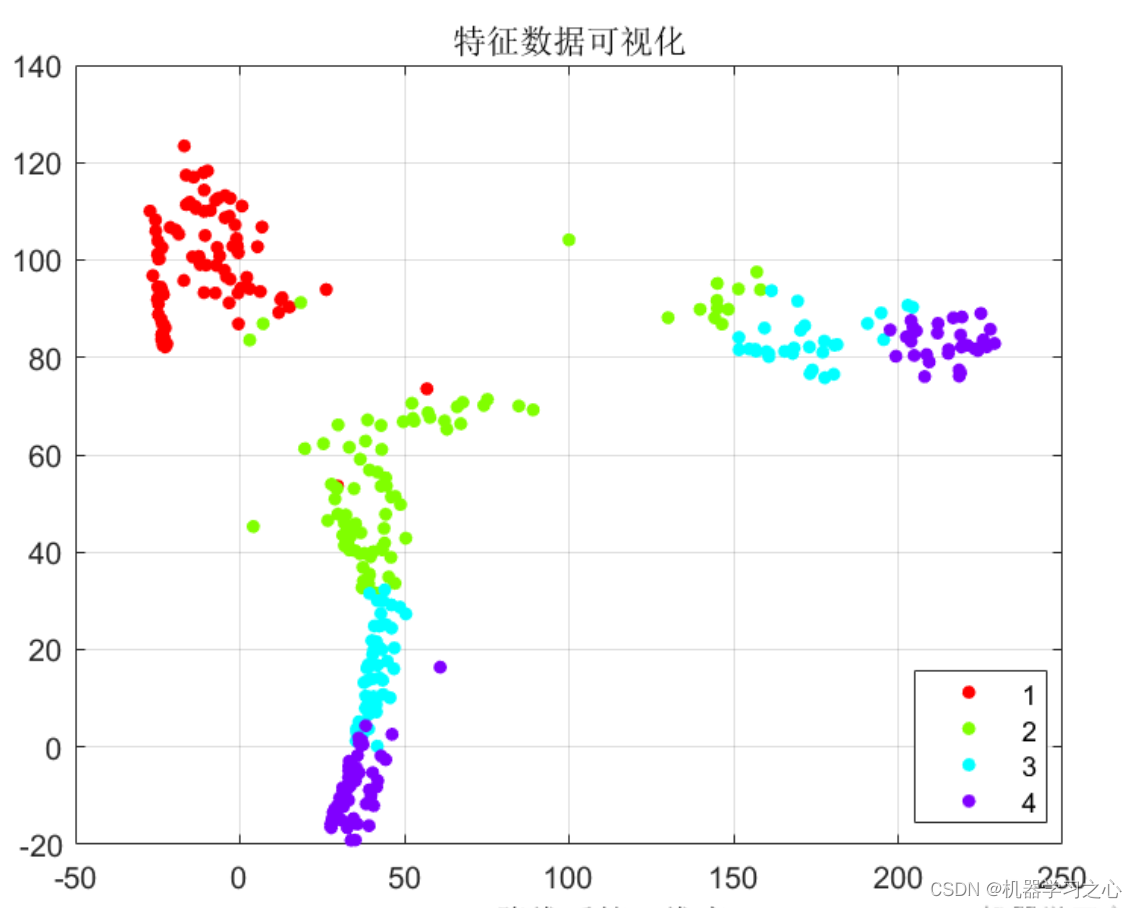
数据降维 | MATLAB实现T-SNE降维特征可视化
数据降维 | MATLAB实现T-SNE降维特征可视化 目录 数据降维 | MATLAB实现T-SNE降维特征可视化降维效果基本描述程序设计参考资料 降维效果 基本描述 T-SNE降维特征可视化,MATLAB程序。 T-分布随机邻域嵌入,主要用途是对高维数据进行降维并进行可视化&…...
)
蓝桥杯上岸每日N题 (交换瓶子)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 题目描述 有 N 个瓶子,编号 1∼N,放在架子上。 比如有 5 个瓶子: 2 1 3 5 4 要求每次拿起 2 个瓶子,交换它们的位置。 …...
GMS基本模块TIN、Solids、Modflow2000/2005、MT3DMS、MODPATH。及其在地下水流动、溶质运移、粒子追踪方面的应用
解决地下水数值模拟技术实施过程中遇到的困难,从而提出切实可行的环境保护措施,达到有效保护环境、防治地下水污染,推动经济社会可持续发展的目的。 (1)水文地质学,地下水数值模拟基础理论;&am…...
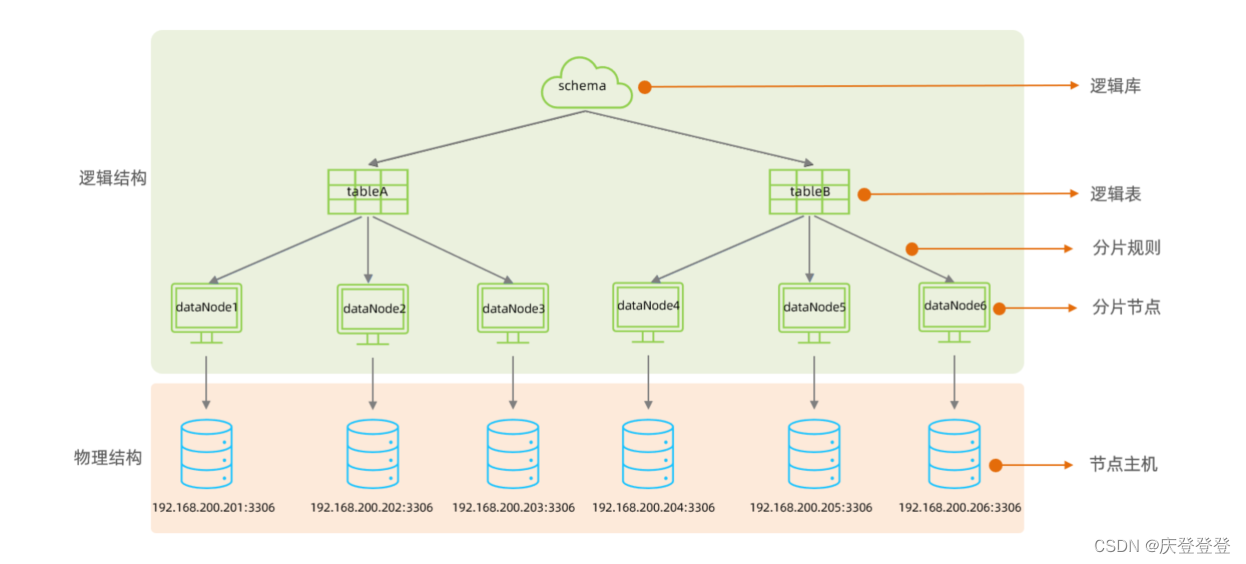
MySQL数据库中间件Mycat介绍及下载安装(教程)
一,介绍 MyCat是开源的、活跃的、基于Java语言编写的MySQL数据库中间件。可以像使用MySQL一样来使用MyCat,对于开发人员来说根本感觉不到MyCat的存在。 开发人员只需要连接MyCat即可,而具体底层用到几台数据库,每一台数据库服务器…...
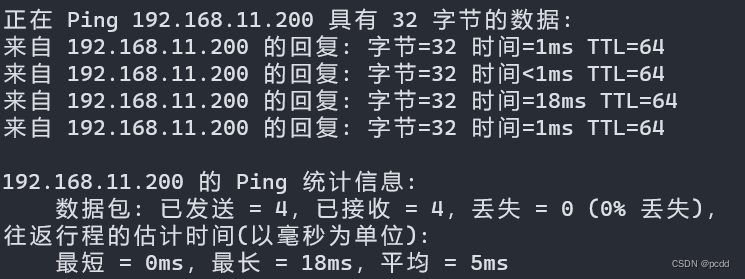
【VMware】CentOS 设置静态IP(Windows 宿主机)
文章目录 1. 更改网络适配器设置2. 配置虚拟网络编辑器3. 修改 CentOS 网络配置文件4. ping 测试结果 宿主机:Win11 22H2 虚拟机:CentOS-Stream-9-20230612.0 (Minimal) 1. 更改网络适配器设置 Win R:control 打开控制面板 依次点击&#x…...
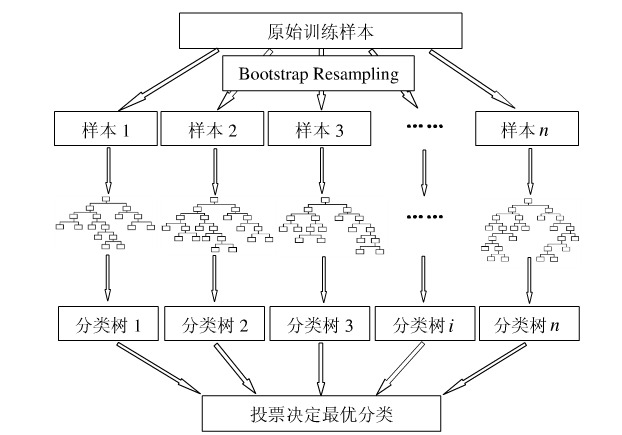
机器学习十大算法之七——随机森林
0 引言 集成学习(ensemble learning)是时下非常流行的机器学习算法,它本身不是一个单独的机器学习算法,而是通过在数据上构建多个横型,集成所有模型的建模结果,基本上所有的机器学习领域都可以看到集成学习…...
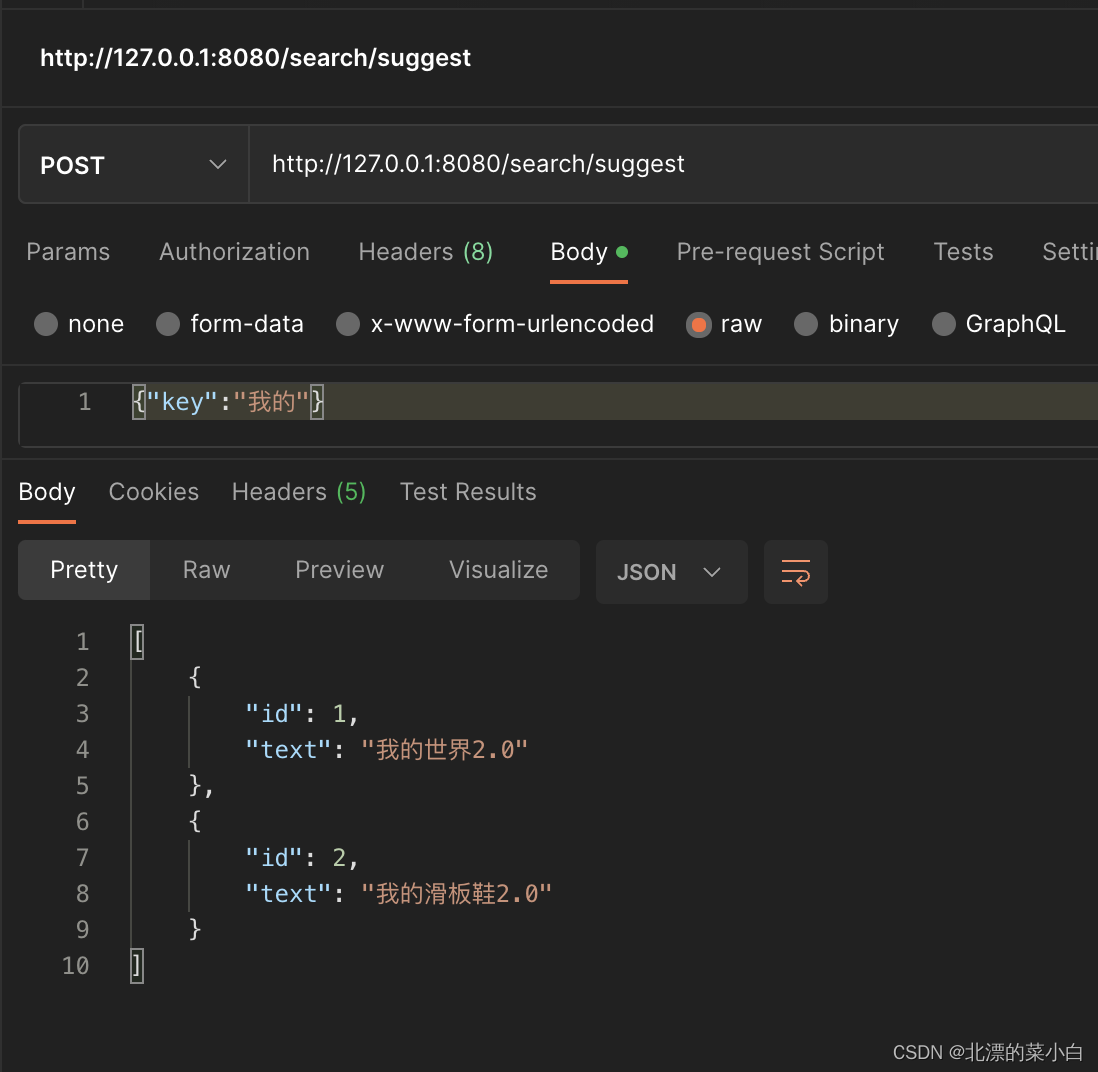
spring boot 3使用 elasticsearch 提供搜索建议
业务场景 用户输入内容,快速返回建议,示例效果如下 技术选型 spring boot 3elasticsearch server 7.17.4spring data elasticsearch 5.0.1elasticsearch-java-api 8.5.3 pom.xml <dependency><groupId>org.springframework.boot</gr…...

住宅IP:解锁更快速、稳定的互联网,你准备好了吗?
随着互联网的广泛普及,我们对网络的需求也越来越高。无论是工作、学习还是娱乐,我们都希望能够享受到更快速、稳定的互联网连接。而在实现这一目标的过程中,住宅IP正逐渐崭露头角,成为了一种备受关注的解决方案。那么,…...

支持dolby vision的盒子接支持dolby vision的电视,在adaptive hdr时,播放非dv的hdr视频,输出sdr
支持dolby vision的盒子接支持dolby vision的电视,setting选择adaptive hdr,按照这个配置在播放非dv的hdr视频时,会输出sdr。 看起来是很不合理的,高级的产品播放高级的片源,却输出低级的画质。 想要搞清楚这个问题&am…...
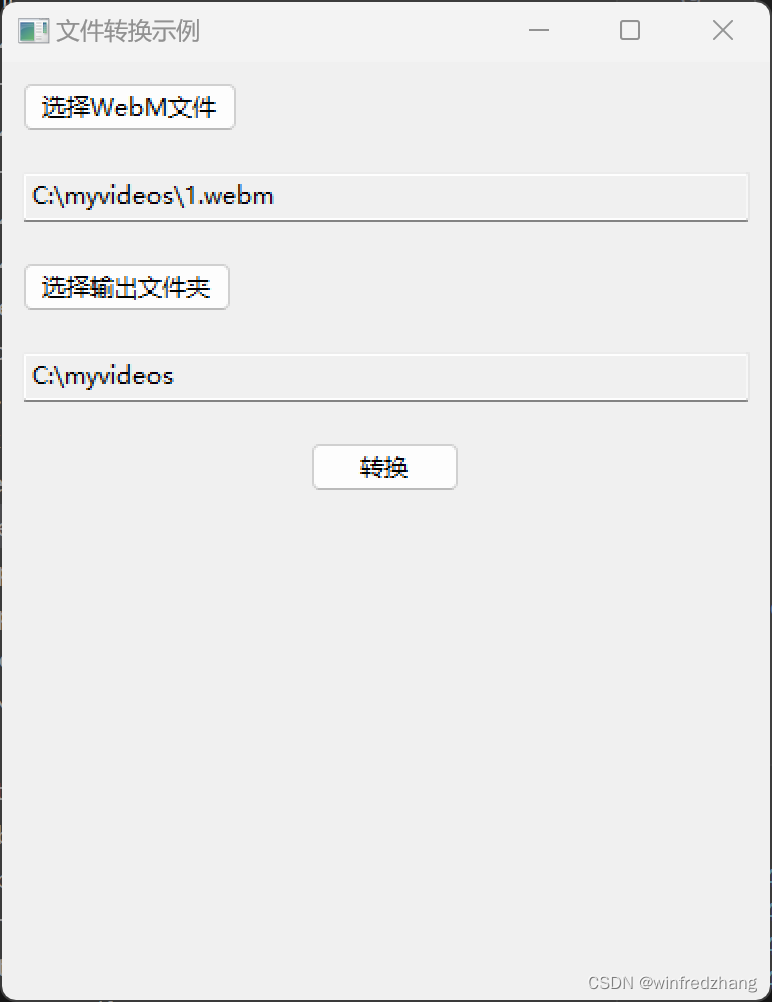
使用ffmpeg将WebM文件转换为MP4文件的简单应用程序
tiktok网上下载的short视频是webm格式的,有些程序无法处理该程序,比如roop程序,本文介绍了如何使用wxPython库创建一个简单的GUI应用程序,用于将WebM文件转换为MP4文件。这个应用程序使用Python编写,通过调用FFmpeg命令…...

Prompt-“设计提示模板:用更少数据实现预训练模型的卓越表现,助力Few-Shot和Zero-Shot任务”
Prompt任务(Prompt Tasks) 通过设计提示(prompt)模板,实现使用更少量的数据在预训练模型(Pretrained Model)上得到更好的效果,多用于:Few-Shot,Zero-Shot 等…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
