第五、六章 贪心算法、回溯算法
贪心算法
适合于贪心算法求解的问题具有:贪心选择性质、最优子结构性质。
贪心算法可以获取到问题的局部最优解,不一定能获取到全局最优解。
贪心算法总是作出在当前看来最好的选择;并且每次贪心选择都能将问题化简为一个更小的与原问题具有相同形式的子问题。
活动安排问题
回溯算法
应用回溯法求解时,需要明确定义问题的解空间。
旅行商问题–>使用排列数解决。
用约束函数在扩展结点处剪去不满足约束条件的子树;
用限界函数剪去不能得到最优解的子树。
三个步骤:
1.针对所给问题,定义问题的解空间;
2.确定易于搜索的解空间结构;
3.以深度优先的方式搜索解空间,并且在搜索过程中使用剪枝函数避免无效搜索。
子集树:
void backtrack (int t) // 形参t为树的深度,根为1
{if(t>n){update(t);return;}for(int i=0;i<2;i++){x[t]=i;if(constrant(t)&&bound(t))backtrack(t+1);}
}
排列树:
void backtrack (int t) // 形参t为树的深度,根为1
{if(t>n){update(t);return;}for(int i=0;i<2;i++){x[t]=i;if(constrant(t)&&bound(t))backtrack(t+1);}
}
素数环问题
int n,a[N],ans;
bool vis[N];
int check(int x,int y)
{int sum=x+y;for(int i=2; i*i<=sum; i++)if(sum%i==0) return 0;return 1;
}
void dfs(int x)
{if(x==n+1){if(check(a[n],a[1]))ans++;return;}for(int i=1;i<=n;i++){if(!vis[i]&&check(i,a[x-1])){vis[i]=1;a[x]=i;dfs(x+1);vis[i]=0;}}
}
void solve()
{cin>>n;dfs(1);cout<<ans<<endl;
}
最优装载问题
#include <bits/stdc++.h>
#define endl '\n'
#define int long longusing namespace std;
const int N =7e3+5;
const int inf=1e18;
const int mod=1e9+7;
const double eps=1e-8;
int n,c,a[N],sum,bestcw,b[N],ans[N];
void dfs(int x,int cw)
{if(x==n+1){if(cw>bestcw){for(int i=1;i<=n;i++) ans[i]=b[i];bestcw=cw;}return;}sum-=a[x];if(cw+a[x]<=c) //约束函数{b[x]=1;cw+=a[x];dfs(x+1,cw);cw-=a[x];}if(cw+sum>bestcw) //限界函数{b[x]=0;dfs(x+1,cw);}sum+=a[x];
}
signed main()
{cin>>n>>c;for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];dfs(1,0);cout<<bestcw<<endl;return 0;
}
/*
4 34
21 10 5 2
*/回溯算法 实现01背包:
#include <bits/stdc++.h>
#define endl '\n'
#define int long longusing namespace std;
const int N =7e3+5;
const int inf=1e18;
const int mod=1e9+7;
const double eps=1e-8;
int n,c,cw,cv,bestv;
struct node
{int w,v;double d;
}a[N];
bool cmp(node a,node b)
{return a.d>b.d;
}
double check(int x)
{int tmp=c-cw;double v=cv;while(x<=n&&a[x].w<=tmp)tmp-=a[x].w,v+=a[x].v,x++;if(x<=n) v+=1.0*tmp*a[x].d;return v;
}
void dfs(int x)
{if(x==n+1){bestv=cv;return;}if(cw+a[x].w<=c){cw+=a[x].w;cv+=a[x].v;dfs(x+1);cw-=a[x].w;cv-=a[x].v;}if(check(x+1)>bestv)dfs(x+1);
}
signed main()
{cin>>c>>n;for(int i=1;i<=n;i++){cin>>a[i].w>>a[i].v;a[i].d=a[i].v*1.0/a[i].w;}cout<<1<<endl;sort(a+1,a+n+1,cmp);dfs(1);cout<<bestv<<endl;return 0;
}
/*
50 3
10 60
30 120
20 100
*/n皇后问题
法一:
int n,m,a[105][105],tag[105][3],ans;
void dfs(int x)
{if(x==n+1){ans++;return;}for(int i=1;i<=n;i++){if(!tag[i][0]&&!tag[i+x][1]&&!tag[30+i-x][2]){tag[i][0]=1;tag[i+x][1]=1;tag[30+i-x][2]=1;dfs(x+1);tag[i][0]=0;tag[i+x][1]=0;tag[30+i-x][2]=0;}}
}
法二:
#include <bits/stdc++.h>
#define int long long
#define lowbit(x) ((x)&(-x))
#define endl '\n'
#define lowbit(x) (x&(-x))
using namespace std;
const int N = 7e6+100;
const int mod = 998244353;
int n,m,a[105][105],p[N],ans;
int check(int x)
{for(int i=1;i<x;i++)if(abs(x-i)==abs(p[x]-p[i])||(p[i]==p[x]))return 0;return 1;
}
void dfs(int x)
{if(x==n+1){ans++;for(int i=1;i<=n;i++)cout<<p[i]<<" ";cout<<endl;return;}for(int i=1;i<=n;i++){p[x]=i;if(check(x))dfs(x+1);}
}
signed main()
{//ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;dfs(1);if(ans)cout<<ans<<endl;elsecout<<"No Solution!"<<endl;return 0;
}图的m着色问题
解空间的大小为m^n种
相关文章:

第五、六章 贪心算法、回溯算法
贪心算法 适合于贪心算法求解的问题具有:贪心选择性质、最优子结构性质。 贪心算法可以获取到问题的局部最优解,不一定能获取到全局最优解。 贪心算法总是作出在当前看来最好的选择;并且每次贪心选择都能将问题化简为一个更小的与原问题具有…...
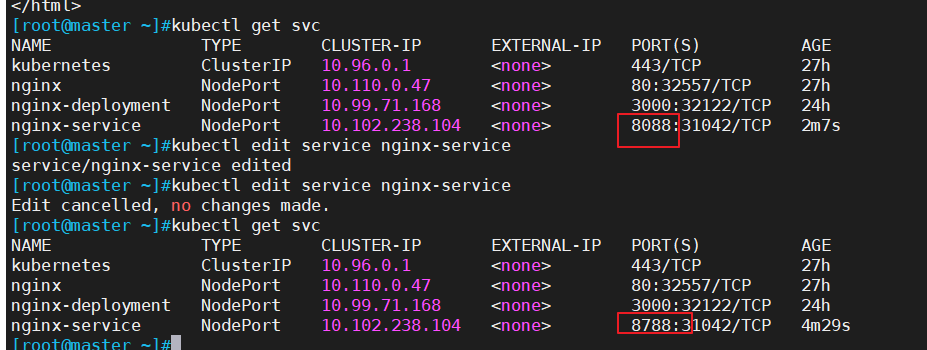
k8s-kubectl命令
文章目录一、kubectl 基本命令1、陈述式资源管理方法:2、声明式资源管理办法二、基本信息查看三、项目的生命周期创建kubectl run命令四、金丝雀发布(Canary Release)——陈述式管理方法五、声明式管理方法kubectl create 和 kubectl apply区别一、kubectl 基本命令 1、陈述式…...
36、基于51单片机频率计 LCD 1602显示系统设计
摘要 数字频率计是一种基本的测量仪器。它被广泛应用于航天、电子、测控等领域,还被应用在计算机及各种数学仪表中。一般采用的是十进制数字,显示被测信号频率。基本功能是测量正弦信号,方波信号以及其他各种单位时间内变坏的物理量。由于其…...
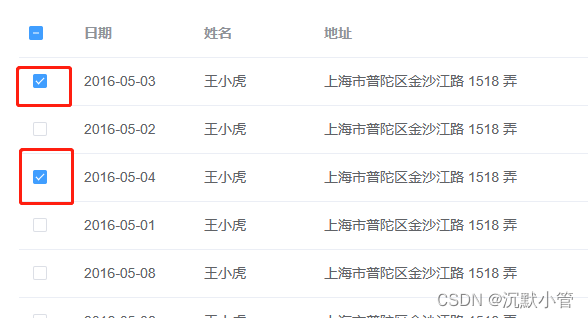
【vue】elemente-ui table toggleRowSelection 默认选择无效[已解决]
项目场景: 点击按钮,弹出一个弹出框,内部出现一个table表,表内数据是动态获取,同时得勾选上几个table表的数据,类似以下的图 问题描述 点击按钮显示弹出框,加载table中的数据,默…...
 HttpMessageConverter扩展)
SpringMVC DispatcherServlet源码(5) HttpMessageConverter扩展
前文通过阅读源码,深入分析了DispatcherServlet及相关组件的工作流程,本文不再阅读源码,介绍一下扩展HttpMessageConverter的方式。 HttpMessageConverter工作方式及扩展方式 前文介绍过,HttpMessageConverter是读写请求体和响应…...

day16_API
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、String 三、StringBuffer&StringBuilder 四、日期 零、 复习昨日 见晨考 一、String String代表字符串,类,java程序中的所有字符串&…...

十二月券商金工精选
✦研报目录✦ ✦简述✦ 按发布时间排序 华宝证券 主动暴露的得与失—从Barra框架到私募指增因子分析方法 发布日期:2022-12-01 关键词:股票、Barra、风险暴露、指数增强 主要内容:本文针对私募指数增强产品的策略流程,设计…...

JUnit
Junit 简介 JUnit是一个开源的java单元测试框架,它是XUnit测试体系架架构的一种体现 是Java语言事实上的标准单元测试库真正的优势来自于JUnit所采作用的思想和技术,而不是框架本身。推动了单元测试、测试先行的编程和测试驱动的开发JUnit衍生了许多xUn…...

MySQL学习笔记4-乐观锁和悲观锁
1.定义 乐观锁和倍灌水是并发控制采用的技术手段,确保当多个数位同时对数据中同一数据存取时,不会破坏事物的隔离性、统一性和数据库统一性 乐观锁 假定不会发生并发冲突,只在提交操作时检测是否违反数据完整性 实现方式: 记录…...

踩大坑:json格式存储wav二进制内容
需求描述: 需要将wav音频文件以二进制的形式读出,存放到 json 中,发送post请求到服务,服务解析json,得到二进制内容后放进ASR模型得出转录结果。 记一次坑: # 将wav以二进制形式读出存放到json中 f ope…...

加入CSDN的一年,我收获了这些……
加入CSDN的一年,我收获了这些……加入CSDN的一年,我收获了这些……加入CSDN的一年,我收获了这些…… 🚀🚀时光如白驹过隙般,飞逝而过。一转眼,我就已经是一名大二的学生了,也已经在…...
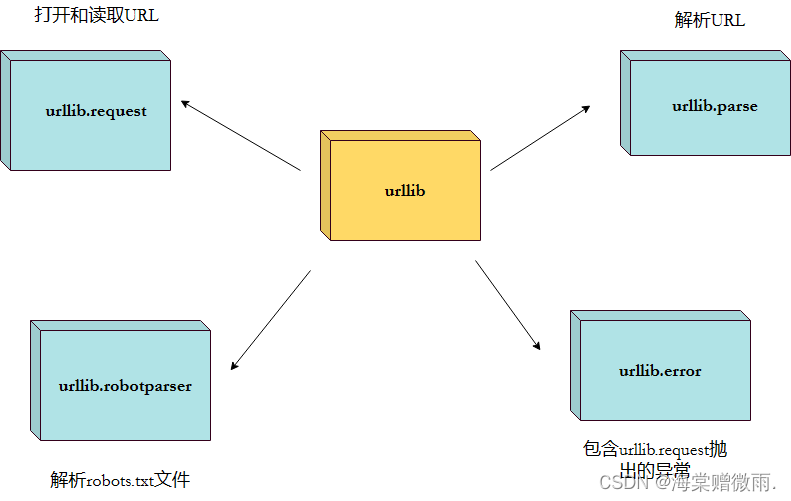
【Python学习笔记】44.Python3 MongoDB和urllib
前言 本章介绍Python的MongoDB和urllib。 Python MongoDB MongoDB 是目前最流行的 NoSQL 数据库之一,使用的数据类型 BSON(类似 JSON)。 PyMongo Python 要连接 MongoDB 需要 MongoDB 驱动,这里我们使用 PyMongo 驱动来连接。…...
LVS中的keepalived高可用
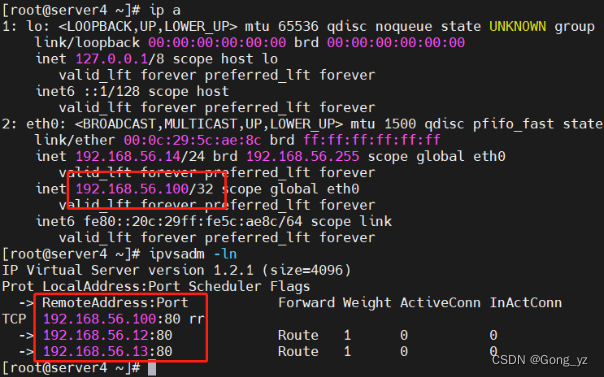
文章目录前言一、Keepalived简介二、keepalived工作原理三、配置文件四、实验1.某台Real Server down2.LVS本身down实验过程:五、代码详细演示整体过程调度器安装软件、设置测试keepalived对后端RS的健康检测backup服务主机设置前言 一、Keepalived简介 Keepalived是…...

【Vue3】组件数据懒加载
组件数据懒加载-基本使用 目标:通过useIntersectionObserver优化新鲜好物和人气推荐模块 电商类网站,尤其是首页,内容有好几屏,而如果一上来就加载所有屏的数据,并渲染所有屏的内容会导致首页加载很慢。 数据懒加载&a…...
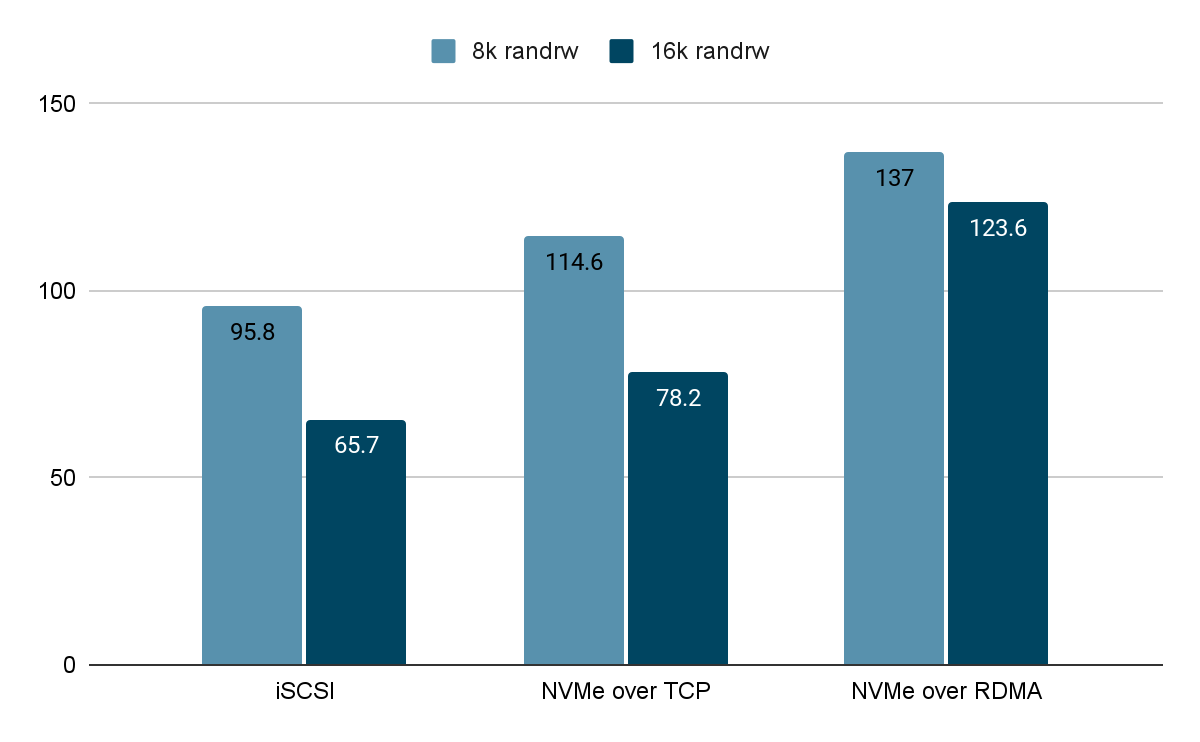
基于 SmartX 分布式存储的 iSCSI 与两种 NVMe-oF 技术与性能对比
作者:深耕行业的 SmartX 金融团队本文重点SmartX 分布式块存储 ZBS 提供 2 种存算分离架构下的数据接入协议,分别是 iSCSI 和 NVMe-oF。其中,iSCSI 虽然具有很多优势,但不适合支持高性能的工作负载,这也是 SmartX 选择…...

Anaconda 安装 Pytorch
下载Anaconda,最新版本的即可,默认安装,最好不要安装在C盘,否则后面C盘容量会很大。 安装Pytorch 打开 Anaconda Prompt ,先切换镜像源为国内清华镜像源,这样安装包的时候下载速度会快一些,也容易成功一些。 在 Anaconda Prompt 命令行依次输入以下四条命令切换到清华镜…...
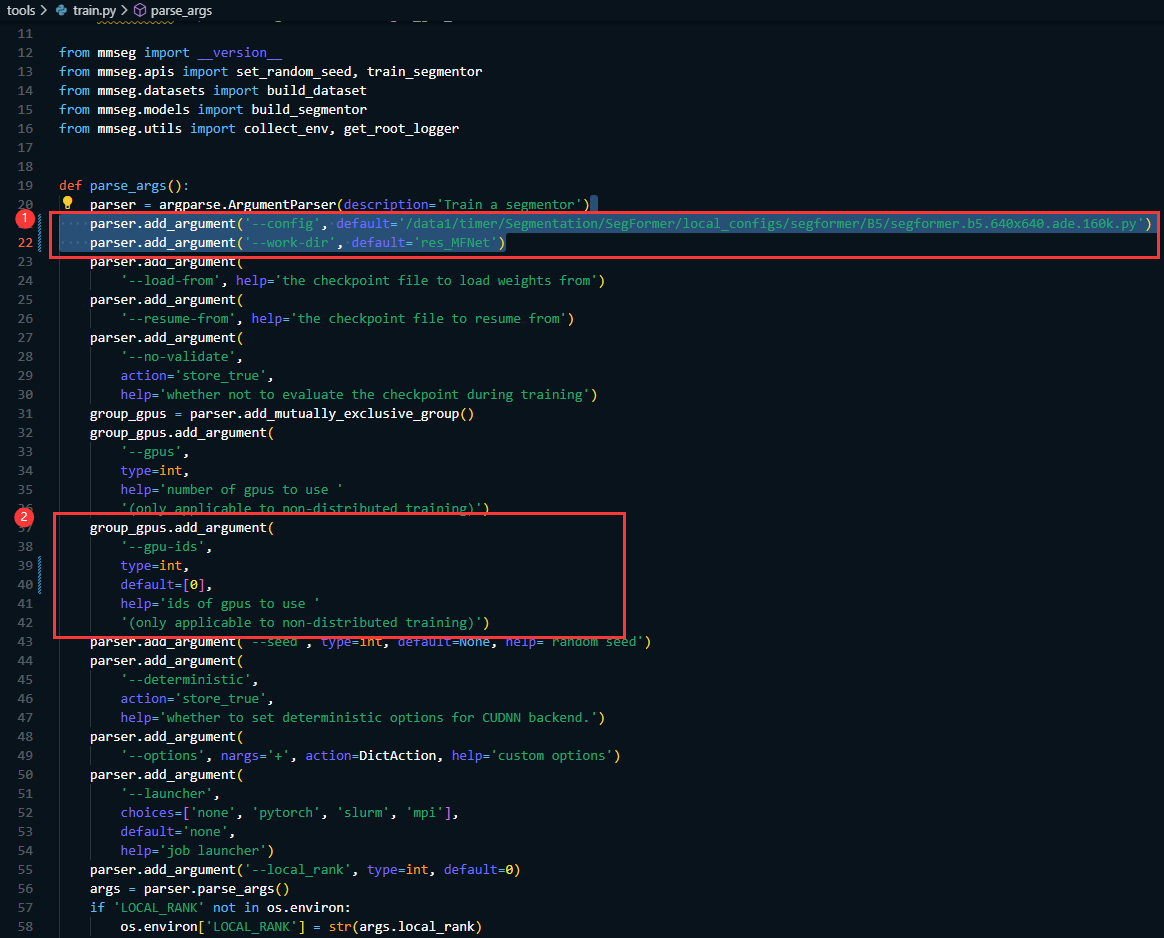
从零开始使用MMSegmentation训练Segformer
从零开始使用MMSegmentation训练Segformer 写在前面:最新想要用最新的分割算法如:Segformer or SegNeXt 在自己的数据集上进行训练,但是有不是搞语义分割出身的,而且也没有系统的学过MMCV以及MMSegmentation。所以就折腾了很久&am…...

会利用信息差赚钱的人才是聪明人
毕业后找不到工作,穷到只剩下时间,大小做了20多份副业兼职,终于找到了可靠的渠道, 我是专科生,学历不好,专业拉胯。毕业后,我找了两三份工作。要么工资太低,只能交房租,…...

【机器学习】Adaboost
1.什么是Adaboost AdaBoost(adapt boost),自适应推进算法,属于Boosting方法的学习机制。是一种通过改变训练样本权重来学习多个弱分类器并进行线性结合的过程。它的自适应在于:被前一个基本分类器误分类的样本的权值会…...
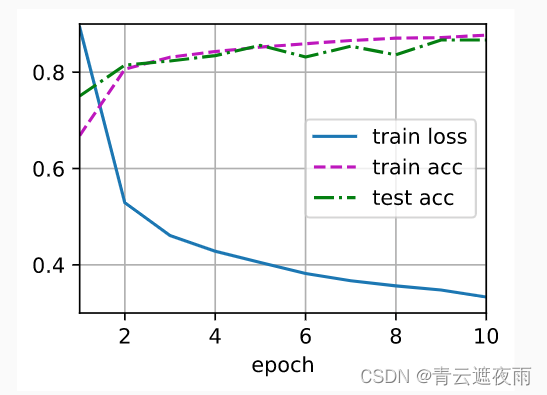
深度学习神经网络基础知识(二)权重衰减、暂退法(Dropout)
专栏:神经网络复现目录 深度学习神经网络基础知识(二) 本文讲述神经网络基础知识,具体细节讲述前向传播,反向传播和计算图,同时讲解神经网络优化方法:权重衰减,Dropout等方法,最后进行Kaggle实…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
